基于多目标优化的悬架系统空间结构稳健性研究

燕宁宁，董恩国

（天津职业技术师范大学汽车与交通学院，天津300222）

基于多目标优化的悬架系统空间结构稳健性研究

燕宁宁，董恩国

（天津职业技术师范大学汽车与交通学院，天津300222）

针对悬架空间结构参数的不确定性对悬架系统性能的影响，在Adams/View中建立了整车参数化模型，以车辆行驶中最大车身垂向加速度、最大侧倾角及最大横摆角速度3个参数为优化目标，以悬架系统的7个空间结构参数为设计变量，对悬架系统进行了传统确定性优化设计和稳健优化设计，并采用蒙特卡洛方法对稳健设计方案进行分析。结果表明：稳健优化设计方案较传统确定性优化方案，目标函数的方差较小，具有较高的稳健性能。

悬架系统；多目标优化；空间结构；稳健性

在车辆悬架系统设计中，传统确定性优化方案保证了系统的最优解，提高了悬架系统的性能。但实际中，悬架机构在装配和制造过程中所产生的随机误差对系统性能的影响不可忽视，因此必须采用稳健设计的方法对悬架系统进行设计研究。车华军等［1］将田口稳健设计的方法应用到悬架参数设计中，提高了车辆的操纵稳定性。董俊红［2］分别选用田口方法和基于响应面的稳健性参数设计方法对悬架参数进行优化设计，改善整车转向特性的同时提高了稳健性。程贤福等［3］运用BBD试验设计方法安排试验，采用双响应面法对悬架系统进行稳健性分析，为悬架系统的研究提出了一种新方法。程市等［4］以悬架关键硬点坐标参数为设计变量，对悬架进行了基于蒙特卡洛统计分析的稳健性优化设计，使目标性能的失效率降低了近90%。Kang等［5］提出了考虑不确定性因素麦弗逊悬架的稳健优化设计，提高了悬架系统性能的稳健性。程贤福等［6］提出了基于Kriging模型和粒子群优化算法的双横臂悬架稳健优化设计方法，提高了双横臂悬架运动性能参数的稳健性。Lee等［7］提出了麦弗逊悬架的稳健优化设计和敏感性分析。

上述文献虽然对悬架系统的稳健性能进行了研究，但并没有考虑悬架的空间结构参数对悬架系统性能的影响。因此，本文综合考虑悬架空间结构参数的不确定性对悬架系统性能的影响，应用蒙特卡洛方法对传统确定性优化结果进行稳健性分析，从而修正设计变量的初始值，提高悬架系统动力学性能的稳健性。

1　整车参数化模型的建立

基于多体动力学软件Adams/View模块，建立包含前后悬架模型、转向系模型、底盘模型、轮胎模型、路面模型等子系统模型在内的整车系统模型。其中，前悬架采用双横臂式独立悬架系统，后悬架选用结构简单的斜置臂式悬架；转向系采用齿轮齿条式转向器，轮胎选用Fiala轮胎，路面模型采用Adams中自带的随机路面模型。整车实体模型搭建完成后即可进行参数化处理，基于参数化模型的基点，创建合理的设计变量，将模型中所有的硬点坐标和构件长度做参数化处理，最终得到的整车参数化模型如图1所示。

图1　整车参数化模型

2　关键参数识别

2.1设计变量

整车参数化建模过程中所创建的设计变量主要分为4大部分：车辆轴距、与前悬架相关的设计变量、与转向系相关的设计变量以及与后悬架相关的设计变量。所创建的设计变量中与前悬架空间结构相关的有上横臂长度（UCA）、下横臂长度（LCA）、拉臂长度（Pull_arm）、悬架弹簧与上横臂铰接点到上横臂外球铰点的距离（Left_UCA_center）、主销长度（kingpin）、主销与转向节铰接点到下横臂外球铰点的距离（kingpinCenter）、主销内倾角（inclination）、主销后倾角（caster）和转向节长度（knuckle）。

考虑影响悬架系统动力学性能的关键空间结构参数，选定UCA、LCA、kingpin、Left_UCA_center、kingpinCenter、inclination和caster 7个参数作为设计变量，设计变量的取值范围如表1所示。

2.2目标函数

为改善悬架系统的动力学性能，提高车辆行驶的操纵稳定性和平顺性，优化目标主要包括车辆行驶过程中最大车身垂向加速度（ACCY）、最大侧倾角（ceqingjiao）和最大横摆角速度（hengbaijiaosudu）。

2.3试验算法

为辨识设计变量对目标性能的影响［8］，提高优化设计精度，基于最优拉丁超立方设计算法，对设计变量进行关键参数的辨识，试验结果如图2所示。

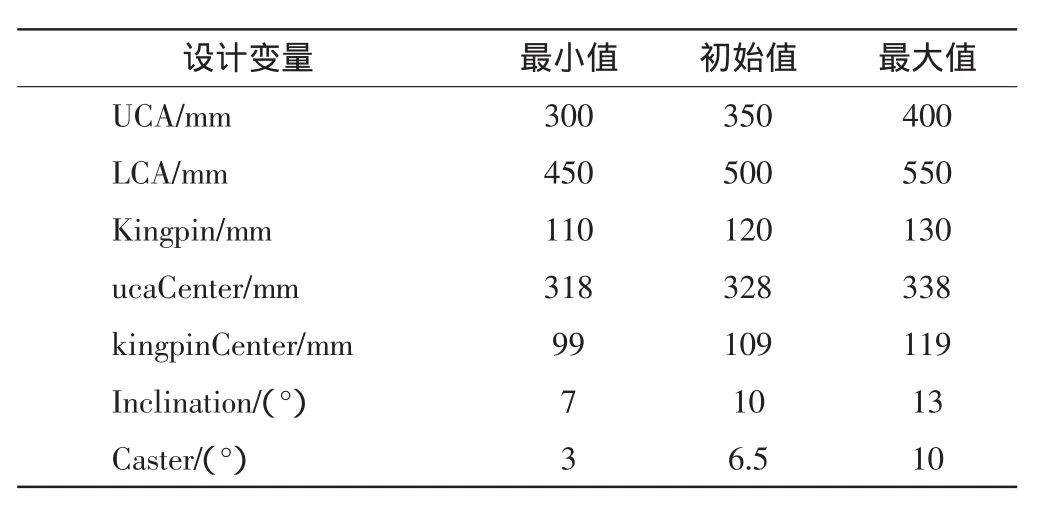
表1　设计变量的取值情况

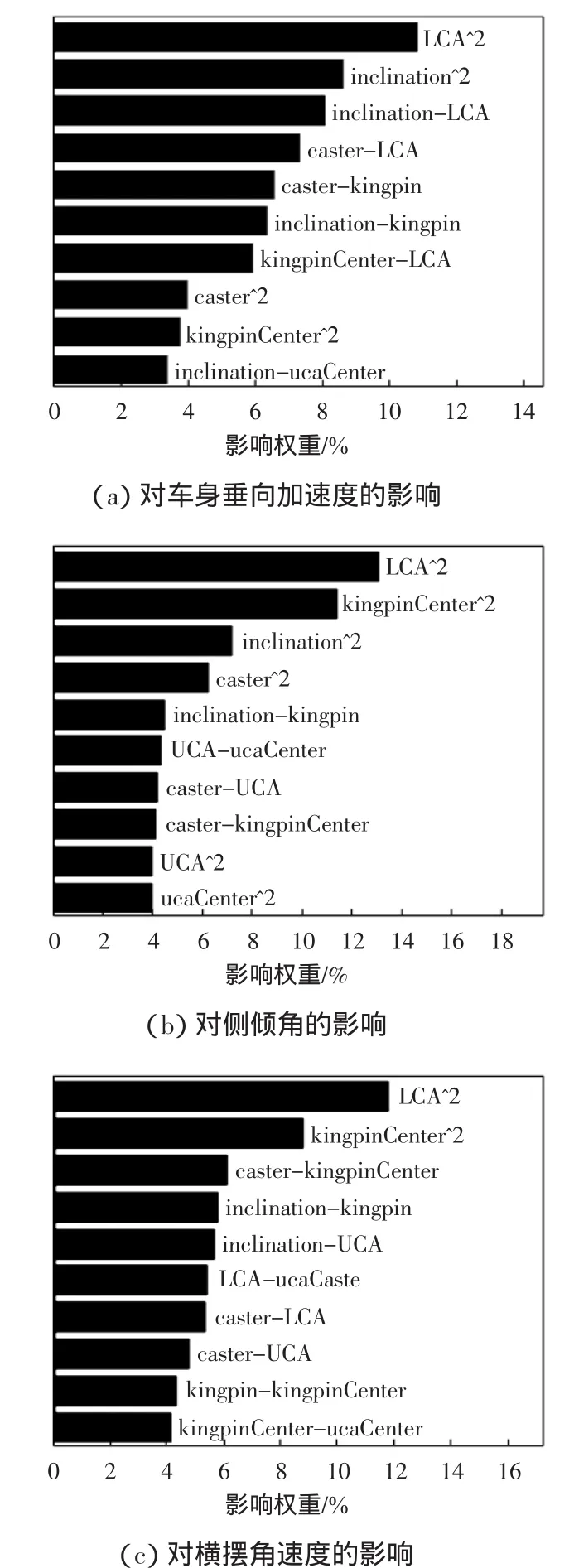
图2　目标函数的影响权重分析

图2（a）、图2（b）和图2（c）分别为设计变量对车身垂向加速度、侧倾角和横摆角速度影响的Pareto图。从图2中可以看出，7个设计变量中，对车身垂向加速度影响较大的因子是LCA和inclination；对侧倾角影响较大的因子是LCA和kingpincenter；对横摆角速度影响较大的因子是LCA和kingpincenter，而其他几个因子对目标性能的影响较小。综合考虑认为LCA、inclination和kingpincenter 3个设计变量为影响目标性能的关键因子。

3　悬架系统的确定性优化

悬架系统空间结构的优化设计是一个多目标的优化问题，为避免优化过程中求解问题陷入局部最优解，因此选用自适应模拟退火算法（adaptive simulated annealing，ASA）来求解悬架系统空间结构参数的最优解问题，它比传统的模拟退火优化算法（SA）具有更好的全局求解能力和计算效率。在对优化算法进行设置时，最大迭代次数取200，每5步检查一次收敛性，收敛精度取默认值1.0×10-8。

传统确定性优化方案的优化结果如表2所示。由表2可知，确定性优化解使目标性能较初始值均有所下降，其中最大车身垂向加速度降幅最大，由30.512 4 m/s2下降到21.436 9 m/s2。同时可以看出，该优化方案中UCA、inclination、caster 3个设计变量的值都非常接近约束边界，UCA的优化值305.182 mm接近其约束下限300 mm，inclination的优化值12.498°接近其约束上限13°，caster的优化值3.083°接近其约束下限3°。若存在不确定因素干扰，该优化设计方案极有可能会违反所设定的约束，因此有必要对该方案进行稳健性分析。

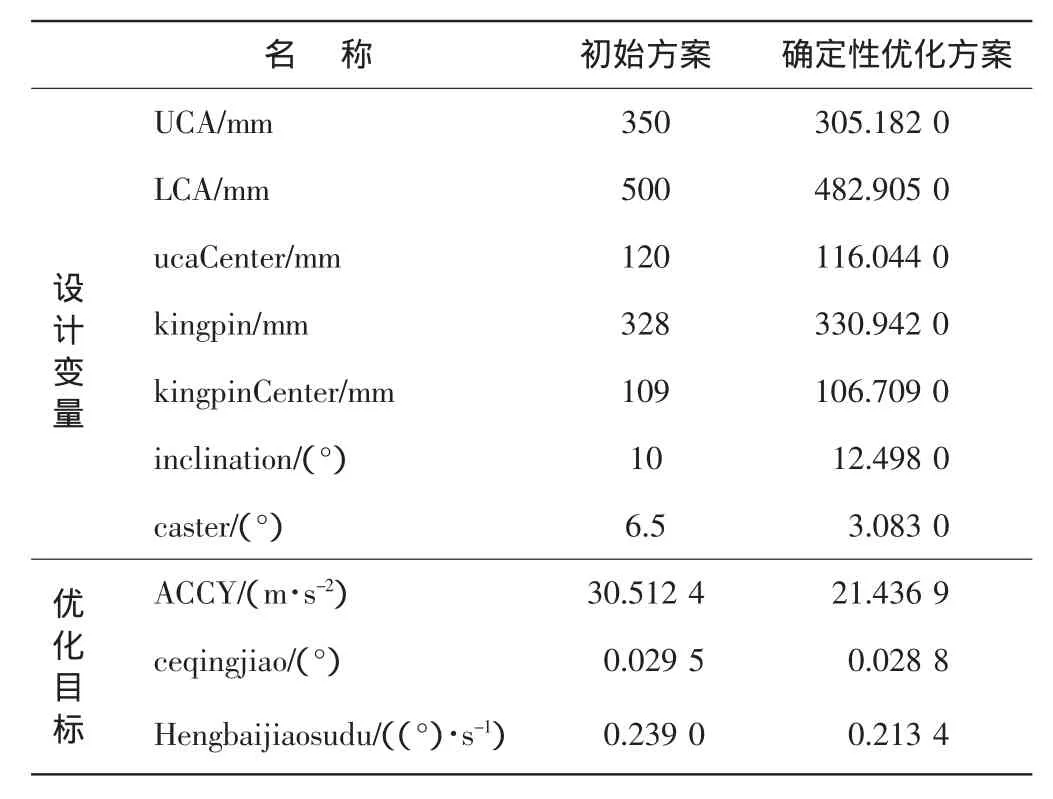
表2　确定性优化结果

4　蒙特卡洛模拟

优化方案选择蒙特卡洛方法进行稳健性分析。蒙特卡洛模拟（monte carlo simulation，MCS）是20世纪40年代中期由数学家冯·诺依曼［9］提出的一种以概率统计理论为基础的数值计算方法，可以用随机数来解决很多计算问题，应用领域非常广泛。

假定各设计变量为服从正态分布的相互独立的随机变量，即X～（μ，σ2），具体分布情况如表3所示。其中LCA、inclination、kingpincenter 3个关键因子的标准差均为0.1，其他非关键因子的标准差为0.05，所有设计变量的均值均为确定性优化设计所得结果。

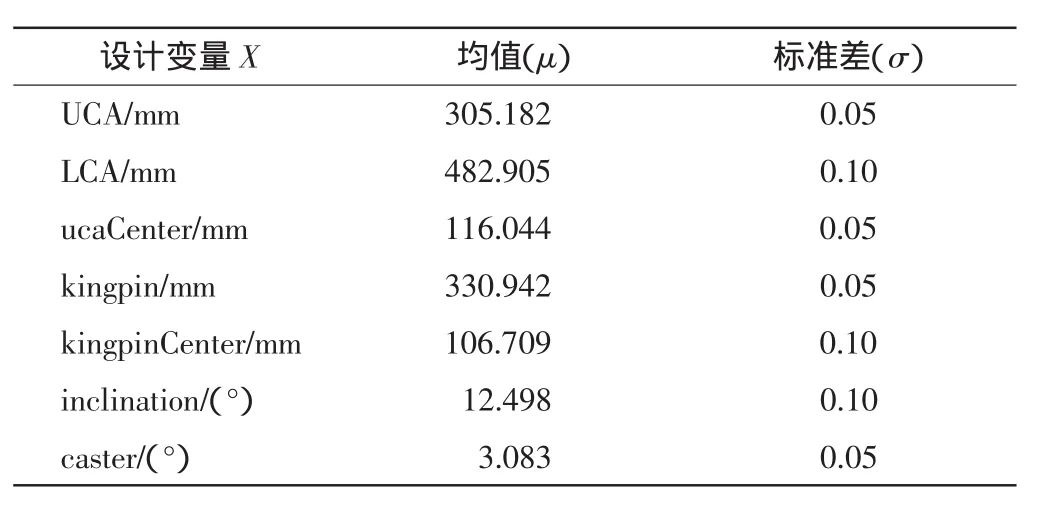
表3　设计变量正态分布情况

稳健优化设计结果如表4所示。选择描述性采样方法，生成100次随机试验，得到各目标函数的概率分布如图3所示。图3（a）为车身垂向加速度的概率分布，ACCY～N（25.793，4.8222）；图3（b）为侧倾角的概率分布，ceqingjiao～N（0.0266，0.002 22）；图3（c）为横摆角速度的概率分布，hengbaijiaosudu～N（0.190，0.016 22）。

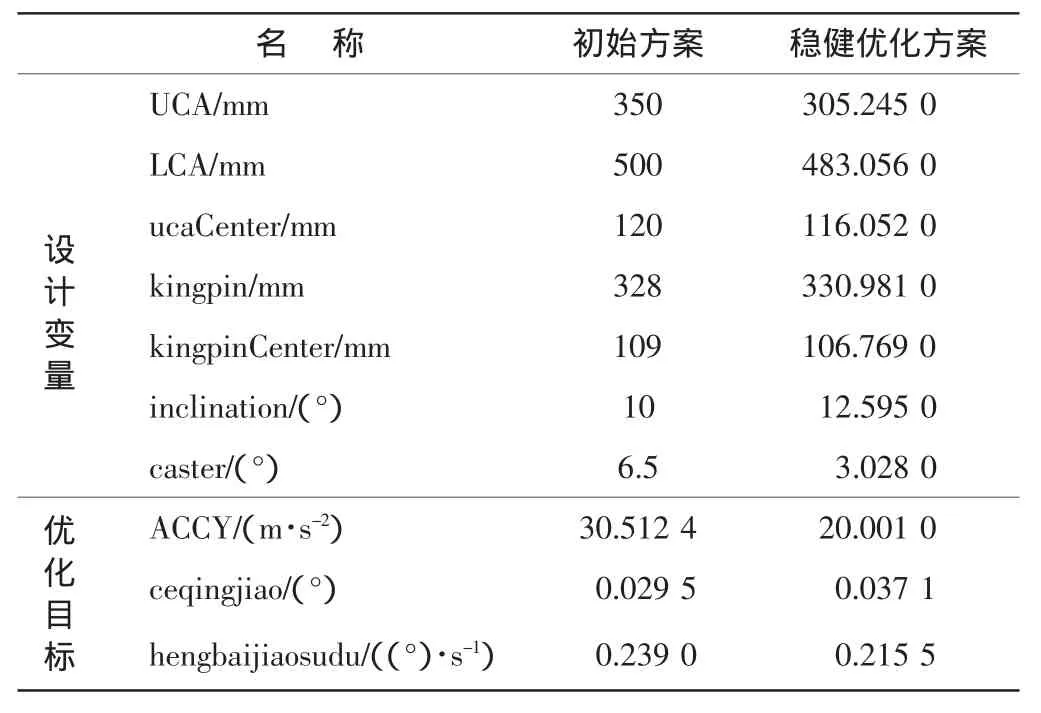
表4　稳健优化设计结果

以稳健优化的结果为基础，再次运用蒙特卡洛方法对悬架系统进行稳健性分析，分析结果如图4所示。由图4可知，各目标函数的概率分布为：ACCY～N（25.641，4.4022），ceqingjiao～N（0.026 2，0.0012），heng－baijiaosudu～N（0.189 2，0.013 22）。目标函数的方差均比确定性优化方案的方差小，说明稳健优化设计方案较传统确定性优化方案具有更高的可靠性。采用蒙特卡洛方法对确定性优化方案和稳健优化方案所得结果进行稳健性分析得到目标函数的均值和标准差如表5所示。

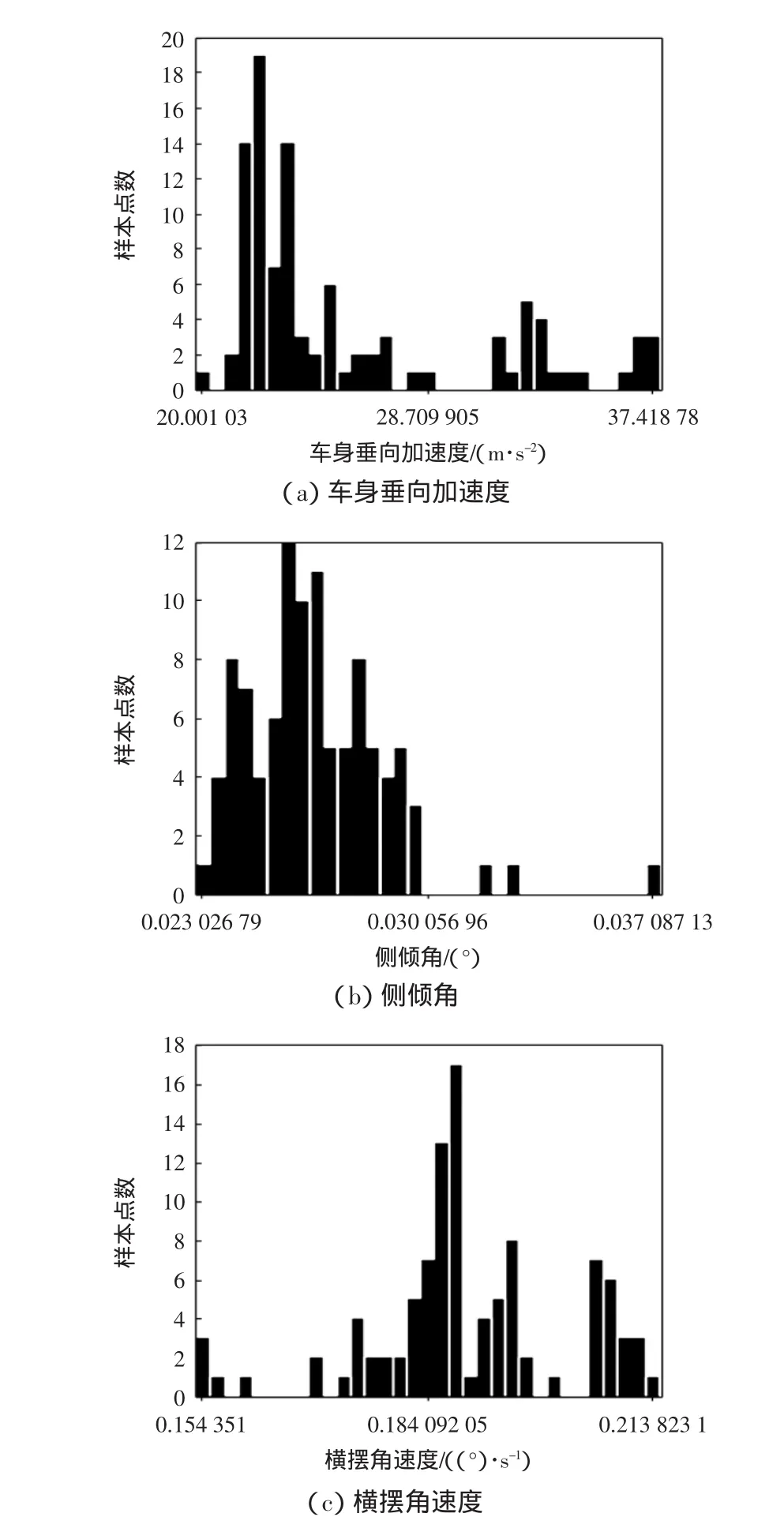
图3　目标函数的概率分布

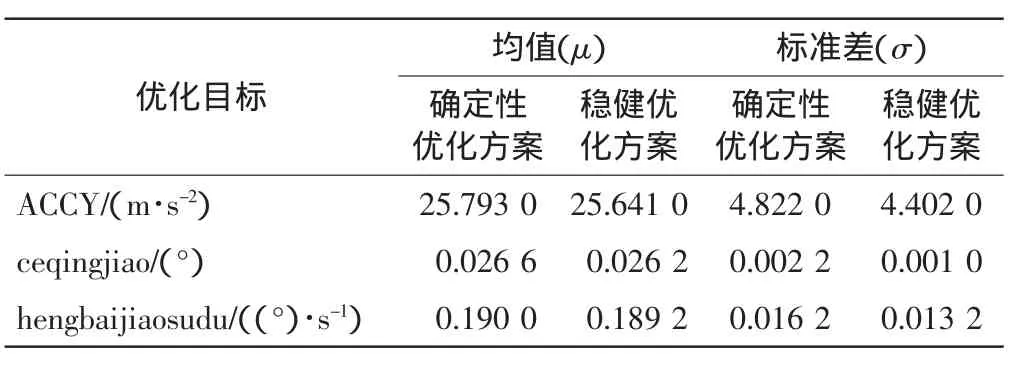
表5　优化方案结果对比

图4　稳健优化后目标函数的概率分布

5　结束语

本文基于Adams/View建立整车参数化模型，采用最优拉丁超立方试验设计算法对设计变量进行关键参数识别，得出影响目标函数的关键因子下横臂长度（LCA）、主销内倾角（inclination）和主销与转向节铰接点到下横臂外球铰点的距离（kingpincenter）。通过蒙特卡洛方法对稳健设计的结果进行分析，结果表明：稳健优化设计方案较传统确定性优化方案，目标函数的方差较小，具有更高的稳健性。

［1］车华军，陈南，殷国栋.基于操纵稳定性的车辆悬架性能参数稳健设计方法［J］.汽车工程，2009，31（4）：371-375.

［2］董俊红.基于微型客车操纵稳定性的悬架参数优化设计［D］.长沙：湖南大学，2010.

［3］程贤福，袁峻萍，吴志强，等.基于双向应面法和BBD的车辆悬架系统稳健设计［J］.华东交通大学学报，2012，29（5）：1-6.

［4］程市，马杉杉.基于蒙特卡洛分析的双横臂独立悬架稳健性优化［J］.农业装备与车辆工程，2015，53（5）：27-32.

［5］KANG D O，HEO S J，KIM M S.Robust design optimization of the McPherson suspension system with consideration of a bush compliance uncertainty［J］.Proceedings of the Institution of Mechanical Engineers，2010，224（6）：705-716.

［6］程贤福，刘艳军，林彧群.汽车双横臂悬架参数稳健优化设计［J］.机械科学与技术，2016，35（9）：1421-1425.

［7］LEE H G，WON C J，KIM J W.Design Sensitivity analysis and optimization of McPherson suspension systems［C］//Proceedings of the World Congresson Engineering.London：WCE，2009：1-6.

［8］HAFTKA R T，MROZ Z.First-and second-order sensitivity analysis of linear and nonlinear structures［J］.AIAA-Journal，1986，24（7）：1187-1192.

［9］METROPOLIS N.The beginning of the Monte Carlo method［J］.Los Alamos Science，1987（15）：125-129.

Research on robustness of spatial structure of suspension system based on multi-objective optimization

YAN Ning-ning，DONG En-guo
（School of Automobile and Transportation，Tianjin University of Technology and Education，Tianjin 300222，China）

In view of the influence of uncertainty of spatial structure parameters of suspension on suspension system performance，a vehicle parametric model is established in Adams/View.The optimization objectives are the maximum vertical acceleration of vehicle body，the maximum roll angle and maximum yaw velocity.The design variables include the spatial structure parameters of 7 of suspension system.A traditional deterministic optimization design and a robustness optimization design of suspension are carried out.The results show that，compared with traditional deterministic optimization，variance of objective was less and the robustness was higher to robustness optimization design.

suspension system；multi-objective optimization；spatial structure；robustness

U463.33

A

2095－0926（2016）03－0010－04

2016-08-18

天津职业技术师范大学科研发展基金项目（KJ15-08）.

燕宁宁（1993—），女，硕士研究生；董恩国（1973—），男，教授，硕士生导师，研究方向为汽车稳健设计和故障诊断.