两方与两方之间的量子秘密共享

邓晓冉

（天津职业技术师范大学理学院，天津300222）

两方与两方之间的量子秘密共享

邓晓冉

（天津职业技术师范大学理学院，天津300222）

提出一个利用二粒子纠缠态并结合纠缠转换的两方与两方之间的量子秘密共享方案。在方案进行过程中多次进行信道安全性检测，且共享密钥的四方相互制约，两两合作才可获得共享密钥，进一步保证了信道的安全性及共享密钥的可用性。

量子秘密共享；纠缠转换；共享密钥；么正操作

量子信息学是近年来发展迅速的一门交叉学科，其2大重要分支量子隐形传态和量子密钥分配均有飞速发展。随着信息时代的到来，对信息安全的要求越来越高，量子密钥分配［1-4］的研究也成为学科研究的热点。自1984年Bennet和Brassard［1］提出第一个利用单量子态的量子密钥分配方案以来，有关量子密钥分配的方案层出不穷，最具代表性的有1991年Ekert［3］提出的利用两粒子纠缠态的E91协议、1992年Bennet［2］提出的利用单量子态的B92协议。1999年Hillery、Buzek和Berthiaume［5］提出的利用三粒子GHZ态的量子秘密共享协议，引发了人们研究量子秘密共享的热潮。关于量子秘密共享，近年来的研究成果多为一方与两方或多方之间的量子秘密共享［6-10］，而两方或多方与两方或多方之间的量子秘密共享方案较少。本文利用较容易制备的两粒子纠缠态并结合么正操作与纠缠交换，提出一个两方与两方之间的量子秘密共享方案，该方案通过多次安全性检测，可有效保证所形成共享密钥的安全性。

1　量子秘密共享协议

量子秘密共享协议方案形成过程如下：

（1）发送方Alice1和Alice2（以下简称A1和A2）各自独立分别制备N个二粒子纠缠态Φ＋〉，A1将手中的N个二粒子纠缠态分为2个粒子序列，分别为｛PA11，PA12，PA13，…，PA1N｝和｛PB11，PB12，PB13，…，PB1N｝；A2也将手中的N个二粒子纠缠态分为2个粒子序列，分别为｛PA21，PA22，PA23，…，PA2N｝和｛PB21，PB22，PB23，…，PB2N｝。然后，A1和A2分别对｛PA11，PA12，PA13，…，PA1N｝和｛PA21，PA22，PA23，…，PA2N｝序列随机执行｛I，σx，iσy，σz｝操作之一，制备态Φ＋〉的转化态如表1所示。之后A1和A2再各自独立将｛PB11，PB12，PB13，…，PB1N｝和｛PB21，PB22，PB23，…，PB2N｝序列分别发送给接收方Bob1和Bob2（以下简称B1和B2）。

（2）B1和B2接收到A1和A2发送的粒子后，通过公共信道（如电话线）告知A1和A2已接收到发送的粒子。

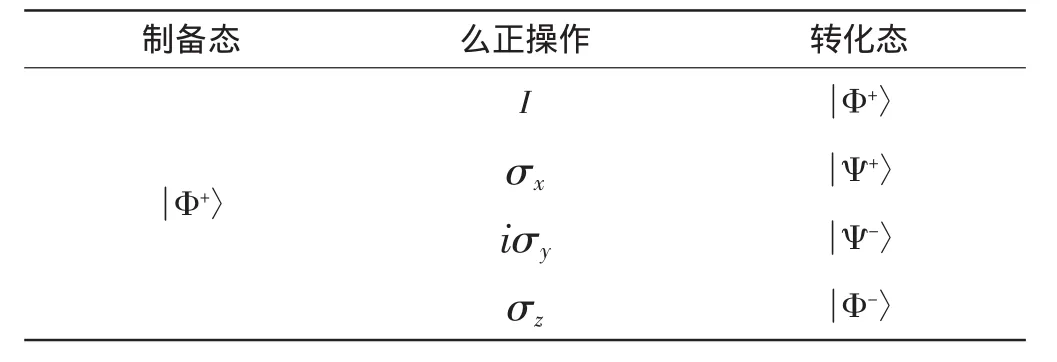
表1　Φ+〉态的么正转换

（3）B1和B2各自独立选择足够多的偶数个量子位并对其两两执行Bell基测量，用于检测信道的安全性，如表2所示。

表2　纠缠转换

（4）B1和B2通过公共信道分别告知A1和A2其各自对哪2个粒子执行了Bell基测量。A1和A2收到信息后，即对手中的对应粒子执行Bell基测量。

（5）B1和B2公布测量结果，A1和A2分别根据B1和B2公布的测量结果得到各自信道的出错率。

（6）A1和A2通过公共信道公布各自信道的出错率，若其中一个信道的出错率高于某一阈值，即终止协议；若两信道均出错率较低，则协议可继续。

（7）A1和A2合作将各自手中的粒子一一对应执行联合Bell基测量。

（8）B1和B2再从手中的粒子中选取一部分，在｛0〉，1〉｝下测量，并公布测量结果。A1和A2根据公布的测量结果估计出错率，若出错率低于一定的阈值，协议继续；否则，协议终止。

（9）B1和B2将各自手中剩余的粒子先执行H转换，再在｛0〉，1〉｝下测量。之后，B1和B2合作将各自所得结果进行模二加，即得共享密钥。B1和B2的H转换及其共享密钥如表3所示。

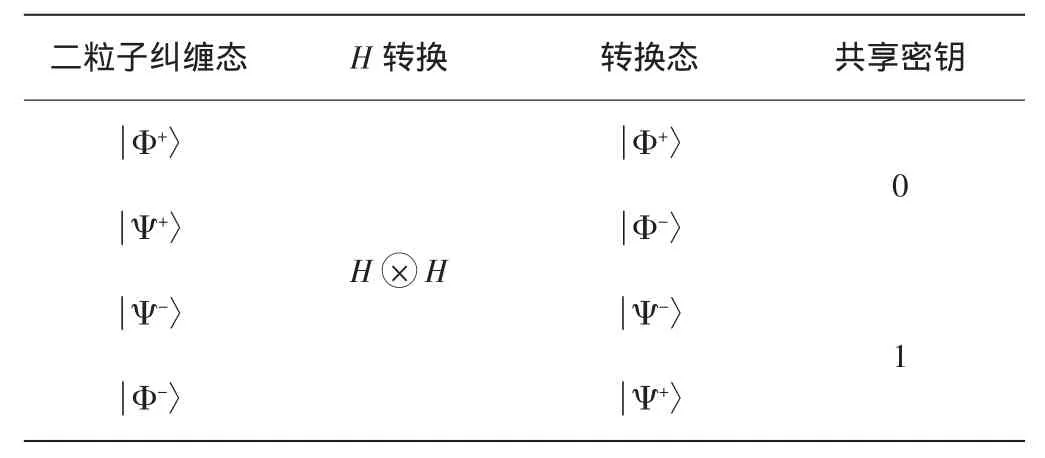
表3　B1和B2的H转换及其共享密钥

（10）A1和A2根据其联合Bell基测量的结果也可得相同的共享密钥，如表4所示。此时A1、A2、B1、B2共享一组密钥。

表4　A1和A2的测量结果及共享密钥

2　安全性分析

在该方案形成共享密钥的过程中多次通过纠缠交换和｛|0〉，|1〉｝正交基测量的方式进行了安全性检测，这些检测可有效抵制来自窃听者的各种攻击，从而保证协议的安全性。

2.1截获-发送攻击

（1）若Eve为B1、B2中的两方之一，在此以B1是Eve为例。B1在接收自己粒子的同时截获了A2发送给B2的粒子，并把事先准备好的C粒子发送给B2，B1的这种窃听行为必将导致A2-B2信道的出错率提高，从而在上文步骤（5）和（6）中被发现，导致协议终止。

（2）若Eve为非B1、B2的第三方，Eve在粒子发送的过程中分别截获了B1和B2的粒子，然后将事先准备好的粒子再分别发送给B1和B2，Eve的这种窃听行为必将导致A1-B1和A2-B2信道的出错率均提高，从而在上文步骤（5）和（6）中被发现导致协议终止。

可见本协议能有效防止截获-发送攻击，保证信道及共享密钥的安全性。

2.2截获-测量-再发送攻击

（1）若Eve为B1、B2中的两方之一，在此仍以B1是Eve为例。B1在接收自己粒子的同时截获了A2发送给B2的粒子，对其进行测量后再将该粒子发送给B2，B1的这种窃听行为将破坏A2-B2的纠缠态，这将在利用纠缠转换进行安全性检测的步骤中被发现，从而导致协议终止。

（2）若Eve为非B1、B2的第三方，Eve在粒子发送的过程中分别截获了B1和B2的粒子，对它们进行测量后再分别发送给B1和B2，Eve的这种窃听行为将破坏A1-B1、A2-B2的二粒子纠缠态，这将在之后利用纠缠转换进行安全性检测的步骤中被发现，从而导致协议终止。

可见本协议也能有效防止截获-测量-再发送攻击，保证共享密钥的安全性。

综上所述，本协议可有效防止Eve可能进行的各种攻击，从而保证协议中的信道及共享密钥的安全性。

3　结束语

本文利用容易制备的二粒子纠缠态结合纠缠交换及么正操作在两方与两方之间形成共享密钥，共享密钥的各方之间相互制约，能有效保证共享密钥的安全性以及信息传递的双向性。

［1］BENNETTCH，BRASSARDG.Quantumcryptography：Public key distribution and coin tossing［C］//In Proceedings of IEEE International Conference on Computers，Systems and Signal Processing.Bangalore：IEEE，1984：175-179.

［2］BENNETT C H，BRASSARD G，MERMIN N D.Quantum cryptography without Bell’s theorem［J］.Physical Review Letters，1992，68（5）：557-559.

［3］EKERT A K.Quantum cryptography based on Bell’s theorem［J］.Physical Review Letters，1991，67（6）：661-663.

［4］BENNETT C H.Quantum cryptography using any two nonorthogonal states［J］.Physical Review Letters，1992，68（21）：3121-3124.

［5］HILLERY M，BUZEK V，BERTHIAUME A.Quantum secret sharing［J］.Physical Review A，1999，59（3）：1829-1833.

［6］XIAO L，LONG G L，DENG F G，et al.Efficient multi-party quantum secret sharing schemes［J］.Physical Review A，2004，69（5）：521-524.

［7］ZHANG X Q，TAN X Q，LIANG C.High efficient multiparty quantum secret sharing scheme［C］//2014 Ninth international Conference on P2P，Parallel，Grid，Cloud and Internet Computing.Guangzhou：IEEE，2014：245-250.

［8］QIN H W，ZHU X H，DAI Y W.A proactive quantum secret sharing scheme based on GHZ state［J］.Modern Physics Letters B，2015，29（27）：1-10.

［9］LIAO C H，YANG C W，HUANG T.Dynamic quantum secret sharing protocol based on GHZ state［J］.Quantum Inf Process，2014，13（8）：1907-1916.

［10］RAHAMAN R，PARKER M G.Quantum scheme for secret sharing based on local distinguishability［J］.Physical Review A，2015，91：1-7.

Quantum secret sharing with two parties and two parties

DENG Xiao-ran
（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

A protocol of quantum secret sharing between two parties and two parties using two-particle entanglement states and entanglement swapping is presented in this paper.The protocol carries on examination to the eavesdropper for many times，furthermore，the four parties mutually restrict each other，and the shared keys can be obtained only if Alice1-Alice2 or Bob1-Bob2 cooperate，so that it can promise the safeness of channel and the usability of the shared keys.

quantum secret sharing；entanglement swapping；shared keys；unitary operation

TP309

A

2095－0926（2016）03－0034－02

2016-03-14

天津职业技术师范大学科研发展基金项目（KJ14-28）.作者简介：邓晓冉（1979—），女，讲师，硕士，研究方向为量子信息.