基于虚拟阵元设计的稀疏基阵的水下正视声学成像

李 鹏，黄兆宇，徐丽华，郑太成，陈金立

(南京信息工程大学 江苏省气象探测与信息处理重点实验室，江苏省气象传感网技术工程中心，江苏省大气环境与装备技术协同创新中心，江苏 南京 210044)



基于虚拟阵元设计的稀疏基阵的水下正视声学成像

李 鹏，黄兆宇，徐丽华，郑太成，陈金立

(南京信息工程大学 江苏省气象探测与信息处理重点实验室，江苏省气象传感网技术工程中心，江苏省大气环境与装备技术协同创新中心，江苏 南京 210044)

成像帧速率低、系统复杂是声学传感器基阵水下正视声学成像方法存在的主要问题.提出一种基于稀疏传感器基阵成像的方法，能提高成像速率和降低系统复杂性.该方法通过虚拟阵元技术优化设计2-D稀疏传感器基阵，并采用发射基阵同步发射编码信号和接收基阵同步接收回波信号的收发方案.仿真结果表明：与多子阵成像方法比较，该方法能够减少系统的复杂性和保证成像质量.

水下成像；声学传感器；稀疏基阵；编码信号

声学成像是光学成像以外用于探索水下世界的主要途径之一.水下声学成像技术已被广泛应用于军事、港口建设、水下工程和搜救等领域.水下声学成像分为声呐成像和正视成像两种形式[1].水下正视声学成像由声呐成像发展而来.声呐成像显示的是目标反射声强的距离-方位信息，在屏幕上目标显示的是背衬2维阴影的亮斑，而正视成像通常形成目标垂直面的图像，也能够形成水平和垂直方向上的2维图像，在屏幕上目标显示的是形状和结构信息.水下正视声学成像中，传感器基阵成像已经发展为一种主要的成像技术[1].目前，传感器基阵成像系统采用多子阵收发方案，需要大量传感器阵元，导致阵元及通道数目增多、系统复杂、体积庞大及制造成本高[2].因此，在传感器基阵相同的前提下，保证成像质量和成像帧率的同时，减少系统复杂程度和降低成本，是传感器基阵正视成像研究领域一项重要的课题[3].

在基于传感器基阵的水下成像中，国内外研究都取得了一些进展.Ling等提出多基阵合成孔径声呐(synthetic aperture sonar,简称SAS)成像，克服了阵元之间的干扰问题，同步实现了成像与参数估计，但该方法成像速率不高[4].Aykin等提出利用2维前视声呐成像系统实现高分辨率的3维成像方法，且利用投影来记录所测物体的特征，实现图像3维重构，但该方法系统缺乏稳定性[5].袁龙涛等提出在波束方向图具有所期望性能的情况下，多次使用模拟退火算法优化3维摄像声呐的2维稀疏基阵，能有效降低系统硬件复杂度，但优化后的基阵性能指标还有待提高[6].潘浩等提出稀疏基阵与多输入多输出(multiple input multiple output，简称MIMO)声呐相结合的低运算量成像方法，使用模拟退火算法对阵元位置进行优化，能获得期望的波束性能，但成像分辨率仍需改善[7].王晓峰采用1维接收线阵和1维正交发射线阵的基阵结构，替代原有的传感器面阵，降低了成像系统的复杂性，但成像质量还需要进一步提高[8].韩业强将分布式并行子阵(distributed and parallel subarray，简称DPS)波束形成算法和模拟退火算法相结合，对接收阵列进行稀疏优化设计，大幅降低了系统的硬件复杂度和成本，但系统的稳定性和分辨率较低[9].受稀疏基阵雷达研究的启发，笔者拟通过虚拟阵元技术优化稀疏传感器基阵，构建一个MIMO水下成像系统.

1 稀疏基阵优化设计

1.1 虚拟阵元技术

虚拟阵元技术可用于稀疏雷达成像和目标参数估计，在保证成像质量和参数估计准确的同时，降低系统的复杂性[10].虚拟阵元技术依据相位中心近似(phase center approximation，简称PCA)原理而形成，其基本思想是：在远场条件下，一对发射和接收分置的阵元，可以由位于它们之间中心位置的一个收发共用的相位中心来替代[11].

图1 虚拟阵元形成示意图Fig.1 Schematic diagram of virtual array element

假设系统采用M个阵元用于发射信号，N个阵元用于接收回波信号，N个通道接收的回波信号经过通道分离，共获得MN路对应收发阵元组合的回波信号.如果采用实阵就需要MN个阵元，比虚拟阵形成的基阵多(MN-(M+N))个阵元，由此可知虚拟阵元技术能够达到降低传感器基阵系统复杂性的目的[12].此外，将优化的正交编码信号与稀疏基阵配合使用，一次发射就可完成一个场景的成像，这对传感器基阵水下正视声学成像帧率的提高尤为重要[13].

1.2 2-D基阵稀疏优化

水下正视成像系统通常采用2-D传感器基阵，笔者采用虚拟阵元技术来实现2-D水下成像基阵的稀疏优化.2-D稀疏基阵优化设计中还需要考虑避免阵元重叠、优化后虚拟基阵的指向性函数、虚拟基阵的物理尺寸等因素[14].

假设优化设计的基阵有M个发射阵元和N个接收阵元.由于回波信号延迟与第m个发射阵元位置tm、目标位置P及第n个接收阵元位置rn有关，根据虚拟阵元技术原理，可将第m个发射阵元发射和第n个接收阵元接收等效为在两个阵元相位中心位置(tm+rn)上的发射和接收[12].假设发射基阵的分布函数ht(x)和接收基阵的分布函数hr(x)分别为

(1)

相应的虚拟基阵的分布函数为

(2)

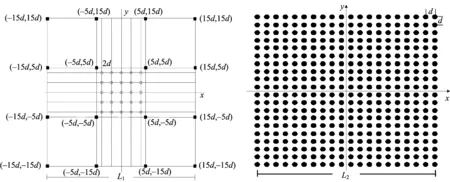
a稀疏基阵 b等效的虚拟基阵图2 16发25收的MIMO稀疏基阵及其PCA等效基阵Fig.2 The MIMO sparse array and the PCA equivalent array of 16 transmitter and 25 receiver

1.3 稀疏基阵波束图

基阵的波束图或指向性函数不仅用于评价基阵性能，还用于确定稀疏后的基阵阵元数目和间距.在远场情况下，假设虚拟阵元均处于XOY平面，X轴方向相邻阵元间距为Δx，Y轴方向相邻阵元间距为Δy，这里令Δx=Δy=d.假设空间向量的单位向量为e，θ为信号向量与Z轴正方向的夹角，φ为信号向量与X轴正方向的夹角.单位向量e可以用θ和φ表示如下

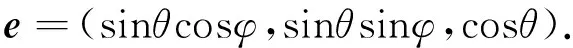
(3)

选取虚拟基阵阵列中心为参考点，则任意一个虚拟阵元(m,n)的坐标可表示为

(4)

则信号入射到虚拟阵元(m,n)上引起的与参考点之间的时延为

(5)

此外，声波从发射阵元到目标的过程中，声波的能量是衰减的，衰减系数为α=αa+αs[15]，其中αa是吸收衰减，αs是散射衰减；同时，声波由目标返回接收阵元的过程中，幅度也有衰减.因此，回波信号的加权表达式为[16]

(6)

其中：σT,σL为波束宽度参数；ε为目标散射系数；r0=10 cm；A0=1；r1,r2分别为发射阵元和接收阵元与目标之间的距离，r1=r2;θ1,φ1,θ2,φ2分别为发射阵元和接收阵元与目标之间形成声线的俯仰角和方位角，θ1=θ2=θ,φ1=φ2=φ.

稀疏基阵波束图的表达式为

(7)

其中：Wmn(r,θ,φ)为幅度加权；θ,φ分别为俯仰角和方位角，θ0,φ0为θ=0,φ=0时波束主瓣的指向；λ为发射信号的波长；M为一行虚拟阵元的个数；N为一列虚拟阵元的个数.当M=N，远场情况下归一化波束图可简化为

(8)

沿X轴和Y轴方向的半功率夹角分别为

(9)

从式(9)可知：基阵的波束宽度与阵元数目及阵元间距有关，即系统分辨率与阵元数目及阵元间距有关.可根据文献[17]中多子阵成像基阵的波束宽度的要求确定优化的基阵.选择发射阵元数目T=4，接收阵元数目R=5.

2 仿真与分析

2.1 波束图仿真

实际成像过程中，为保证较高的成像帧速率，发射阵元应同步发射正交信号，接收阵元应同步接收回波信号，再将接收的回波信号进行通道分离.为简单起见，在不考虑成像速率和成像环境变化的情况下，采用发射阵元逐个发射，接收阵元同步接收回波信号的方案.仿真采用Matlab 2013a软件，16个发射阵元依次发射信号，25个接收阵元同时接收回波信号，每个发射阵元能量相同.此外，仿真中采用线性调频(linear frequency modulation，简称LFM)信号，其相关的表达式为

(10)

(11)

其中：A为脉冲幅度；f0为中心频率；μ为调频斜率.在远场成像区域中，从第m阵元发射出的第n接收阵元接收的信号sr(t)可以表示为

(12)

其中：amn为衰减系数；Δtm为发射阵元到目标点的时延；Δtn为目标反射到接收阵元的时延；n(t)为高斯白噪声.第m阵元发射和第n接收阵元的接收就可以等效为在虚拟阵元(m,n)上进行发射和接收，此回波信号可以表示为

(13)

其中：Δtmn为虚拟阵元(m,n)的时延.对接收到的回波信号进行脉冲压缩处理[18]，脉冲压缩后的信号可以表示为

(14)

(15)

其中：wmn为加权幅度；τmn为虚拟阵元(m,n)的补偿延迟量.通过延时求和波束形成算法，可以得到该成像点的波束图.图3为成像点在基阵正下方Z=-5 m处不同间距的基阵波束图.

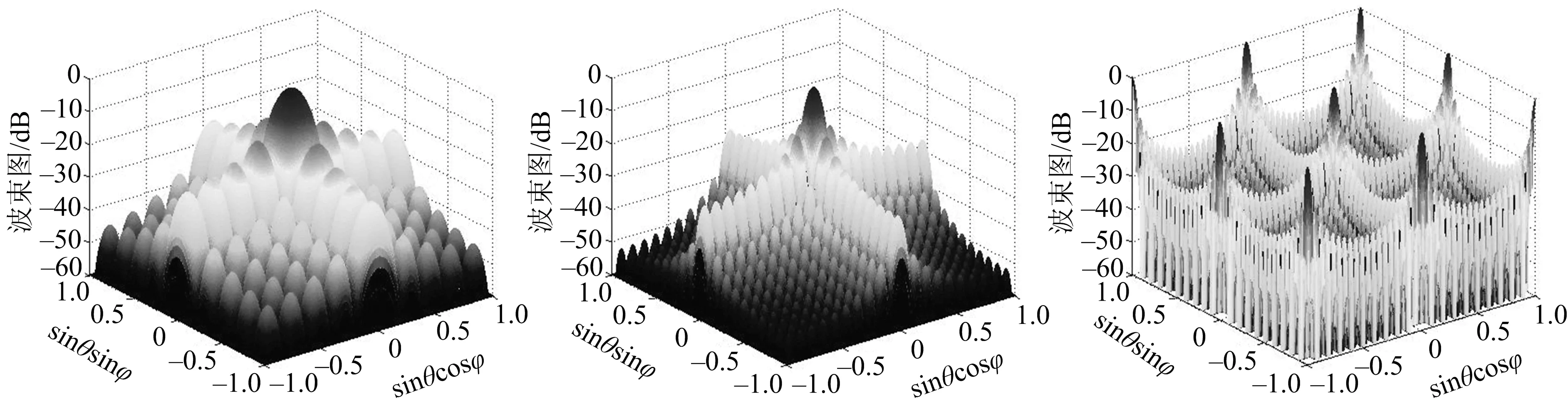
a：d=λ/4； b：d=λ/2； c：d=λ.图3 不同间距的基阵波束图Fig.3 The array beam pattern of different wavelengths

由图3可见，随着虚拟阵元间距的增加，主瓣宽度越窄分辨率越好.当阵元间距d>λ/2时，波束图出现栅瓣.如果间距太小，主瓣的宽度将变宽，成像的分辨率会下降，综合考虑选取d=λ/2，这一点与理论证明是一致的[19].

在多子阵成像方案中，文献[17]采用48×48传感器阵元组成的成像基阵，其中包含64个实子阵，每个实子阵有36个传感器阵元，并形成6×6的阵列.笔者对文献[17]中采用的实子阵进行了仿真，并与优化设计的稀疏基阵进行比较，实子阵波束图仿真中采用收发聚焦方案，以使实子阵波束性能达到最佳.6×6实子阵波束图如图4a所示.将图3b与图4a进行比较，稀疏基阵形成的虚拟基阵的波束主瓣宽度比6×6的实子阵波束的主瓣宽度要窄，说明虚拟基阵可以获得较好的成像分辨率.但是随着实子阵传感器阵元数目的增加，要将实子阵传感器阵元个数提高至20×20，此时传感器阵元数目与形成的虚拟阵元数目相同.20×20的实子阵波束图如图4b所示.由图4b可看出，实子阵的波束分辨率也能达到虚拟基阵的效果，但是整个系统的成像基阵变得非常大，这也意味系统的成本也更高.优化的稀疏基阵的波束主瓣幅度低于子阵的主瓣幅度，并且随着实子阵传感器阵元数目的增加，其子阵波束的幅度也增加，这表明：在阵元特性和发射信号一致的情况下，稀疏基阵成像的探测距离受到限制，比实子阵的成像距离小，但对于近海区域的探测成像，稀疏基阵的性能还是能够满足的，并且能大大节约系统的成本和降低系统的复杂度.

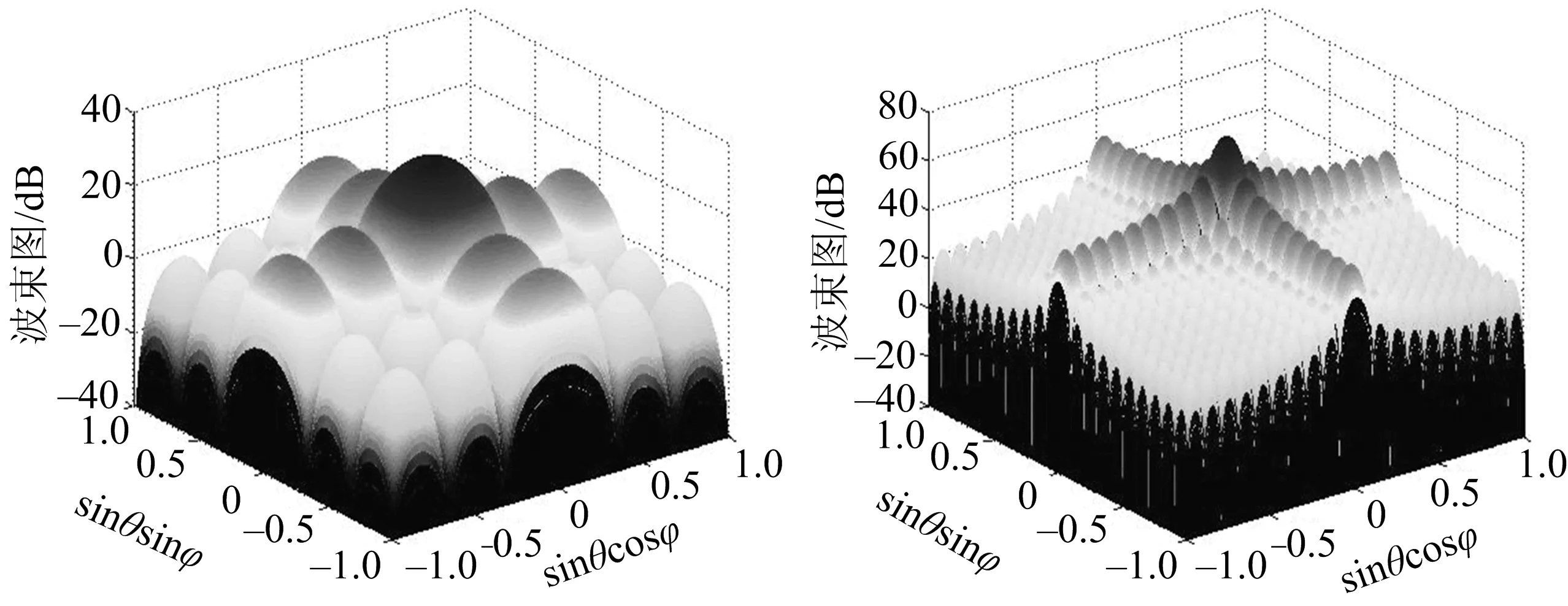
a：6×6的实子阵； b：20×20的实子阵.图4 阵列波束能量强度Fig.4 Array beam energy intensity

2.2 目标成像仿真

进一步对水下点目标和几何目标进行了仿真成像.仿真参数设为：发射信号的带宽30 kHz，中心频率300 kHz，采样率2 MHz，目标点距离0.5 m，水下的声速1 500 m·s-1.根据设置的系统参数和模糊函数理论[20]，可得系统的纵向分辨率为

(16)

其中：B是发射信号的带宽；c是声波在水下传播的速度.图5a,b,c分别是对两个相距2 ，3 ，4 cm的点目标仿真.图5b中的距离是可分辨的最小距离，从图5b中可以看出纵向分辨率为3 cm，与(16)式理论计算一致.

a：2 cm； b：3 cm； c：4 cm.图5 不同间距的两个点目标仿真Fig.5 The results of two point target simulation with different spacing

图6为两个基阵角度分辨率的仿真结果.从图6a可知，稀疏基阵可以分辨出两个目标方向，约为25°和30°；从图6b可知，实子阵可以分辨出一个目标方向，约为26.8°，实子阵的角度分辨率要比稀疏基阵的低.

a:稀疏基阵;b:实子阵.图6 两个基阵的角度分辨率Fig.6 The angle resolution of two receiving array

笔者对几何目标进行了成像仿真，几何目标处于面阵探头下方的成像区域，为便于对目标的观察，将目标放置于成像区域的直角拐角处，设置的目标大小为6 cm×7 cm×5 cm，仿真结果如图7所示.图7表明该文方法可以实现水下目标形状的识别和判断.

图7 几何目标成像结果Fig.7 The imaging result of geometric object

3 结束语

针对传感器基阵成像系统复杂度高和代价大等问题，笔者提出一种基于稀疏基阵的水下正视声学成像方法.基于虚拟阵元技术设计一个2维传感器基阵，通过波束图优化基阵阵元间距，使基阵的波束性能达到最优.通过水下点目标和几何目标的仿真测试，可知点目标有3 cm的纵向分辨率和5°的角度分辨率，几何目标的特征和结构细节明显.传感器基阵可以用于水下正视声学成像，包括对目标形状的识别和判断，稀疏基阵在满足了成像要求的同时，还降低了系统的复杂性和成本.

[1] WOON S G.声学成像技术及工程应用[M].李平,吴文,李虹，等译.北京:机械工业出版社,2013:219-241.

[2] 陈朋.相控阵三维成像声纳系统的稀疏阵及波束形成算法研究[D].杭州:浙江大学生物医学工程与仪器科学学院,2009.

[3] MURINO V,TRUCCO A.Three-dimensional image generation and processing in underwater acoustic vision[J].Proceedings of the IEEE,2000,88 (12):1903-1948.

[4] LING J,XU L,LI J.Adaptiverange-doppler imaging and target parameter estimation in multistatic active sonar systems[J].IEEE Journal of Oceanic Engineering,2014,39 (2):290-302.

[5] AYKIN M D,NEGAHDARIPOUR S.Forward-look 2-D sonar image formation and 3-D reconstruction[C]//Proc IEEE/MTS Oceans’ 12 Conference,2013:1-10.

[6] 袁龙涛,周凡,陈耀武.相控阵三维摄像声纳系统的稀疏阵列优化设计[J].华南理工大学学报 (自然科学版),2013,41 (1):29-37.

[7] 潘浩,孙超,卓颉,等.基于稀疏阵列技术的MIMO声呐低运算量二维成像[J].西北工业大学学报,2014,32 (4):586-592.

[8] 王晓峰.成像声纳波束形成新技术研究[D].哈尔滨:哈尔滨工程大学水声工程学院,2011.

[9] 韩业强.实时相控阵三维成像声纳的波束形成及阵列稀疏技术研究[D].杭州:浙江大学生物医学工程与仪器科学学院,2013.

[10] TARCHI D,OLIVERI F,Sammartino P F.MIMO radar and ground-based SAR imaging systems:equivalent approaches for remote sensing[J].Geoscience and Remote Sensing,IEEE Transactions on,2013,51 (1):425-435.

[11] BELLETTINI A,PINTO M A.Theoretical accuracy of synthetic aperture sonarmicronavigation using a displaced phase-center antenna[J].IEEE Journal of Oceanic Engineering,2002,27 (4):780-789.

[12] LI J,STOICA P.MIMO Radar signal processing[M].New York:Wiley-IEEE Press,2009:75-77.

[13] 韦永梅,彭虎.一种基于非衍射波的高帧率超声成像发射系统的研究[J].物理学报,2014,63 (19):428-433.

[14] HE T,PAN Q,LIU Y G,et al.Near-field beamforming analysis for acoustic emission source localization[J].Ultrasonics,2012,52 (5):587-592.

[15] 冯若.超声手册[M].南京:南京大学出版社,1999:26-28.

[16] LI P,CAI Y,SHEN X,et al.An accurate detection for dynamic liquid level based on MIMO ultrasonic transducer array[J].IEEE Transactions on Instrumentation &Measurement,2015,64 (3):582-595.

[17] 林贤洲,陈耀武.基于分级波束形成的三维声纳系统设计[J].传感器与微系统,2014,33 (8):101-104.

[18] 李鹏,尹杰,王银娟.伪随机编码调制线性调频波的MIMO超声测量方法[J].西安理工大学学报,2014,30 (1):58-62.

[19] 于波,陈客松,朱盼,等.稀布圆阵的降维优化方法[J].电子与信息学报,2014,36 (2):476-481.

[20] 霍凯,姜卫东,黎湘,等.一种新的OFDM相位编码频率步进雷达信号及其特性[J].电子与信息学报,2011,33 (3):677-683.

(责任编辑 郑小虎)

Underwater imaging with the acoustic sensor sparse array optimized by the virtual element method

LI Peng,HUANG Zhaoyu,XU Lihua,ZHENG Taicheng,CHEN Jinli

(Jiangsu Key Laboratory of Meteorological Observation and Information Procession,Jiangsu Meteorological Sensor Network Technology Engineering Center,Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology,Nanjing University of Information Science and Technology,Nanjing 210044,China)

Low frame rate and high system complexity are the main problems of underwater imaging with the acoustic sensor array.One approach using the sparse array to reduce the complexity of imaging system was proposed in this paper.Moreover,the imaging system could obtain a high frame rate if the transmit signal and transmit-receive strategy were appropriate.The sparse array was firstly optimized with the virtual element method,then the orthorhombic coded signal and the synchronous transmit-receive strategy were used for the sparse array.The simulating results showed that the sparse array took on excellent-quality images and significantly reduced the imaging system complexity compared with the multi-subarray.

underwater imaging;acoustic sensors;sparse array;coded signal

10.3969/j.issn.1000-2162.2016.06.010

2016-01-27

江苏省重点研发计划社会发展项目(BE201569)；国家自然科学基金资助项目(41075115)；江苏省第11批六大高峰人才项目(2014-XXRJ-006)；江苏高校优势学科Ⅱ期建设工程项目

李 鹏(1966-),男,山东淄博人,南京信息工程大学副教授,硕士生导师，博士.

TB559

A

1000-2162(2016)06-0051-08