群环的幂等稳定度1
2016-11-18高艳艳
高艳艳
(南京工程学院 数理部,江苏 南京 211167)
群环的幂等稳定度1
高艳艳
(南京工程学院 数理部,江苏 南京 211167)
设a∈R,如果对环R元素b,满足aR+bR=R,则存在幂等元e∈R,使得a+be有左逆,那么称元素a有幂等稳定度1(记为isr(a) =1).如果对于R中的所有元素a,都有isr(a) = 1,那么称环R有幂等稳定度1(记为isr(R) = 1).证明了若R是半完全环,G是初等阿贝尔p-群,则isr(RG) =1.另外,若isr(R)=1,G是局部有限p-群,且p∈J(G),则isr(RG) = 1.
幂等稳定度1;群环;p-群

若群G的每一个有限生成的子群都是有限的,则称G为局部有限群.如果群G的每个元素的阶都是p的方幂,则称G为p-群.如果G的所有非单位元的阶为p,则群G称为初等p-群.众所周知,有限初等交换p-群是有限多个Cp的直积.
在文献[1]中,陈焕银给出了环R具有幂等稳定度1的一些充分必要条件.如果RG具有幂等稳定度1,那么R作为RG的像也必具有幂等稳定度1.笔者将给出这一问题的更多刻画.
对于群环RG,环同态ε:RG→R,∑agg∑ag,称为RG的增广映射且该映射的核,记为给定元素a=∑agg,α的支撑为.文中更多记号和概念详见文献[2-4].
1 预备知识
引理1[1]设R为环.下列陈述等价
(1) isr(R)=1;
(2) 对任意的x,y∈R,都存在一个幂等元e∈R,使得xy-xe+1∈U(R).
命题1 如果R=∏iRi,那么isr(R)=1当且仅当对于所有的i,都有 isr(Ri)=1.
命题2 令φ:RS为环的满同态.如果isr(R)=1,那么isr(S)=1.
证明 设isr(R)=1.令φ:RS为环的满同态.对任意的x1,x2∈S,都存在y1,y2∈R,使得x1=φ(y1),x2=φ(y2).因为isr(R)=1,那么存在幂等元e∈R,使得y1y2-y1e+1=u∈U(R).由于φ是满同态,可得φ(e)是S的幂等元,φ(u) 是S的单位.因此
x1x2-x1φ(e)+1=φ(y1)φ(y2)-φ(y1)φ(e)+1=φ(u)∈U(S).
由定义可知isr(S)=1.
注1 命题2的逆命题是不正确的.设R=Ζ(7),G=C3.显然可见Ζ7C3是 Ζ(7)C3的同态像.因为Ζ7C3是Artin 环,所以它是半完全的.由文献[5]可知,isr(Ζ7C3) = 1.但是 Ζ(7)C3不是clean环,因此也有isr(Ζ(7)C3).
命题3 设I为R的理想,假设I⊆J(R).那么isr(S)=1当且仅当isr(R/I)=1,且幂等元模I可以提升.
证明 “⟹” 如果isr(S)=1,那么R/I作为R的像,有isr(R/I) = 1.任取a∈R,有aR+(-1)R=R.那么存在幂等元e∈R,使得a-e=u∈U(R),进而可知a=e+u.那么R是clean环.由文献[6]可知幂等元模I能够提升.
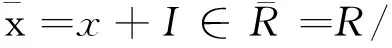
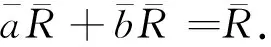
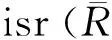
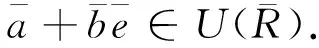
由假设可以设 e2=e∈R.另一方面,存在v∈R,使得
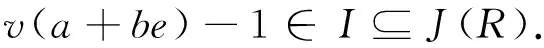
因此可知a+be有左逆,证毕.
推论1[1]设R为环.下列陈述等价
(1) isr(R)=1;
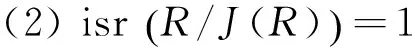
注2 设R[x]为多项式环,那么由文献[7]知R[x]不是clean 环,进而可得isr(R[x])≠1.
但是,对R上的幂级数环R[[x]],情形则截然相反.
命题4 设S=R[[x]],那么isr(S)=1 当且仅当isr(R)=1.
证明 设α=a0+a1x+a2x2+…∈S和β=b0+b1x+b2x2+…∈S.因isr(R)=1,那么存在幂等元e∈R,使得
a0b0-a0e+1∈U(R).
因此
其中:l1,l2…∈R.那么isr(S)=1.
因为R为S的同态像,所以必要性显然可见.
2 主要结果
引理2 设G为群.如果对G的每个有限生成子群H,都有isr(RH)=1,那么isr(RG)=1.
证明 对任意的 x,y∈RG,令H=
注3 引理2的逆命题是不正确的.令R=Z(7),G=S3为3次对称群.由文献[8]可知RG是半完全的.因此由文献[5]可知isr(RG)=1.但是对子群C3≤S3,Ζ(7)C3不是clean环.因此 isr(Ζ(7)C3)≠1.
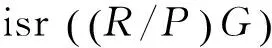
引理3 如果isr(R)=1并且2∈U(R),G是初等Abel 2-群,那么isr(RG)=1.
证明 可以假设G是有限群.那么G是n 个C2的直积,其中n≥1.因为2∈U(R),则RC2≅R⊕R,同样2是RC2的单位,有
R(C2×C2)≅(RC2)C2≅RC2⊕RC2≅R⊕R⊕R⊕R.
类似地可证明RG同构于2n个R的直和.证明完毕.
定理1 设R为半完全环,G是初等Abel 2-群,那么isr(RG)=1.
证明 任取x,y∈RG.令 H=
首先,证明如果R是局部环,那么RG是半完全环.如果2∈U(R),由引理3知RG≅R2n.RG是半完全环.如果2∉U(R),则2∈J(R).因为G是有限2-群,由文献[9]可知RG是局部环,进而可知RG是半完全环.
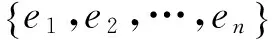
推论2[10]如果R是局部环,G是初等Abel 2-群,那么RG是clean环.
命题6 设n≥2为正整数.则下列陈述等价
(1) isr(RCn)=1,对任意的半完全环R;
(2) isr(RCn)=1,对任意的局部环R;
(3)n= 2.
证明 (1)⟹ (2) 和 (3) ⟹ (2) 是显然的.
(2) ⟹ (1).由定理1可得此结论.
(2)⟹ (3).如果n>2,由文献 [11] 可知,存在素数q,使得Ζ(q)Cn不是clean环.那么isr(Ζ(q)Cn) ≠1,与已知矛盾.
命题7 如果R是布尔环,G是局部有限群,那么isr(RG)=1.
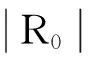
命题8 如果R是局部环,p∈J(R)且G=Cp×C2×…×C2( n 个 C2),其中p是奇素数,那么isr(RG)=1.

引理4[12]设R为环,G为群.如果H是G的子群,那么J(RH)⊇RH∩J(RG).特别地,当H= 1时,有 J(R)⊇R∩J(RG).
引理5[10]设p为素数且p∈J(R).如果G是局部有限p-群,那么Δ(RG)⊆J(RG).
引理6 设p为素数且p∈J(R).如果G是局部有限群且G=HK,其中K是G的正规p-群,H 是G的子群.如果isr(RH)=1,那么isr(RG)=1.
证明 任取g∈G,都存在k∈K和h∈H,使得g=kh=(k-1)h+h∈∑k∈K(1-k)RG+RH.所以 RG=∑k∈K(1-k)RG+RH.由引理6可得Δ(RK)⊆J(RK).因为G是局部有限的,所以G/K也是局部有限的,因此由文献[9]可得J(RK)⊆J(RG).那么,Δ(RK)⊆J(RK),这就证明了 ∑k∈K(1-k)RG⊆Δ(RK)(RG)⊆J(RG).因此得到
RG=J(RG)+RH.
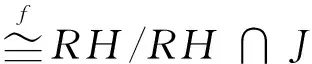
定理2 设p为素数且p∈J(R).如果isr(R)=1,G是局部有限p-群,那么isr(RG)=1.
证明 在引理6中取 H = {1} 即可得证.
由文献[7],知道 Ζ(7)C3不是clean的.因此定理2中的条件 p∈J(R)是必要的.
例1 设p>2为一个素数,Dp是阶为2p的二面体群.如果isr(R)=1且p∈J(R),那么isr(RDp)=1.
证明 令 Dp=
命题9 设R为环,G为群.给定x∈RG,如果isr(x)≠1,那么存在R的真理想I,使得R/I没有非平凡的幂等元,并且isr(x+RG)≠1.
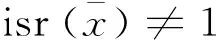
如果R/I有非平凡的幂等元,那么对R的真包含I的理想I1和I2,有
R/I=I1/I×I2/I,
因此
RG/IG≅(R/I)G≅I1G/IG×I2G/IG,
(1)
RG/I1G≅(RG/IG)(I1G/IG)≅I2G/IG,
(2)
RG/I2G≅(RG/IG)(I2G/IG)≅I1G/IG.
(3)
令(x1+IG,x2+IG)∈I1G/IG×I2G/IG 为x+IG在同构 (1)下的像.由I中的极大性可知,isr(xk+IG)=1,其中x+IkG∈RG/IkG(k=1,2).那么由式(2)和式(3)可知isr(xk+IG)=1,其中xk+IG∈IkG/IG(k=1,2).由式(1)可知isr(x+IG)=1,其中x+IG∈RG/IG,与假设矛盾.证毕.
由于没有非平凡中心幂等元的交换环是局部环,有如下推论:
推论3 设R为交换环.如果isr(RG)≠1,那么存在R的真理想I,使得R/I是局部的并且isr((R/I)G)≠1.
设a为环R中的元素,如果存在n>0,使得an∈anRan那么a称为π-正则元.当然如果R中每一个元素都是π-正则元,那么环R称为π-正则环.
引理7[10]如果非零整数k在环R中是π-正则的,那么存在R的一个直和分解R=R1⊕R2,使得 k∈U(R1)且k在R2中是幂零的.
命题10 如果isr(R)=1,G是初等阿贝尔2-群.假设2∈R是 π-正则元,那么isr(RG)=1.
证明 由引理7知R=R1⊕R2,其中2∈J(R1)和2∈U(R2),所以 RG=R1G⊕R2G.因为isr(R1)=1且isr(R2)=1,由定理2 和引理3可知isr(R1G)=1且isr(R2G)=1.综上可得,isr(RG)=1.
[1] CHEN H Y.Rings with many idempotents[J].Internat J Math Sci,1999,22 (3):547-558.
[2] LAM T Y.A first course in noncommutative rings[M].New York:Springer-Verlag,2001.
[3] PASSMAN D S.The algebraic structure of group rings[M].New York:Wiley-Interscience,1977.
[4] POLCINO MILIES C,SEHGAL S K.An introduction to group rings[M].Dordrecht:Kluwer Academic Publishers,2002.
[5] WANF Z,CHEN J L,KHURANA D,et al.Rings of idempotent stable range one[J].Algebra Represent Theory,2012,15:195-200.
[6] NICHOLSON W K.Lifting idempotent and exchange rings[J].Trans Amer Math Soc,1977,229:269-278.
[7] HAN J,NICHOLSON W K.Extensions of clean rings[J].Comm Algebra,2001,29:2589-2595.
[8] WOODS S M.Some results on semiperfect group rings[J].Can J Math,1976,26:121-129.
[9] NICHOLSON W K.Local group rings[J].Can Math Bull,1972,15:138-139.
[10] ZHOU Y Q.On clean group rings[J].Advance in Ring Theory Trends in Math,2009 (1):335-345.
[11] CHEN J L,ZHOU Y Q.Strongly clean power series rings[J].Proc Edinb Math Soc,2007,50:73-85.
[12] CONNELL I G.On the group rings[J].Can J Math,1963,15:650-685.
(责任编辑 朱夜明)
Group rings of idempotent stable range one
GAO Yanyan
(Department of Mathematics and Physics,Nanjing Institute of Technology,Nanjing 211167,China)
An element a in a ring R is said to have idempotent stable range 1 (written isr(a) = 1) if aR+bR=R(for any b∈R) implies there exists an idempotent e∈R,such that a+beis left invertible.If isr(a) = 1 ,for all a∈R ,then R,is called to have idempotent stable range 1 (written isr(R) = 1 ).In this paper,we showed that if R was semiperfect and G was an elementary abelian p-group,then isr(RG) = 1.It was shown that if isr(R) = 1 and p∈J(G)and G was a locally finite p-group,then isr(RG) = 1.
dempotent stable range 1;group ring;p-group.
10.3969/j.issn.1000-2162.2016.06.005
2015-01-11
国家自然科学基金青年科学基金资助项目(11301071);江苏省青年基金资助项目(BK20160771);南京工程学院引进人才科研启动基金资助项目(YJK201340)
高艳艳(1983-),女,山西晋中人,南京工程学院讲师,博士.
O175
A
1000-2162(2016)06-0019-05
