基于Chebyshev神经网络的非线性动态系统预测

李 喆

(新疆大学 网络与信息技术中心,新疆 乌鲁木齐 830046)



基于Chebyshev神经网络的非线性动态系统预测

李 喆

(新疆大学 网络与信息技术中心,新疆 乌鲁木齐 830046)

针对非线性动态系统的预测常受到噪声或其他过程的耦合影响，使得规律变得难以发现的问题，提出了以一组Chebyshev正交基函数作为神经网络中各隐神经元的激励函数的新型的Chebyshev基函数神经网络预测模型.将该模型作为非线性动态系统预测模型，并采用基于粒子群和模拟退火组成的文化基因算法优化神经网络的权值，可以达到很高的预测精度和很好的预测结果.Chebyshev神经网络与传统的BP(back propagation)神经网络相比，工作量大大减少，加快了收敛性.文化基因算法用于确定权值的Chebyshev神经网络分别与粒子群和模拟退火优化的Chebyshev神经网络相比具有更好的拟合效果.

Chebyshev神经网络；非线性动态系统；文化基因算法；预测

在实际的工程领域和科学研究中，许多系统都可以看做是一类存在较高不完整性和随机性的非线性动态时变系统[1]，很难利用确定的机理模型进行描述与预测.由于神经网络具有高度的非线性映射特性和高度的并行计算能力，近年来被广泛用来解决实际的预测问题，在很多领域都取得了成功的应用[2-5].但对于高度非线性的动态系统，用于预测的神经网络模型会更加复杂，权值更难确定.针对这些问题，笔者将Chebyshev神经网络[6-7]与文化基因算法[8-9]相结合，构造了一种基于文化基因算法优化的Chebyshev神经网络预测模型.

Chebyshev神经网络具有网络结构简单、学习收敛速度快、高精度逼近任意非线性映射等优异特点[10-11]；文化基因算法(memetic algorithm，简称MA)是一种全局的种群进化与局部的个体学习的协同，能很好地解决高维优化问题寻优过程中易陷入局部最优的不足.因此，将该模型用于非线性动态系统的预测问题中，能取得很高的预测精度和预测结果.

1 Chebyshev神经网络预测模型

令x=cosθ，则θ=arccosx.则由下式定义的函数是x的n次正交多项式.

笔者采用第一类正交基函数，由定义1可得出递推公式为

(1)

Chebyshev神经网络预测模型如图1所示[12].

图1 Chebyshev神经网络预测模型Fig.1 The model of Chebyshev neural network

2 文化基因算法

Meme是 R.Dawkins于 1976年首次提出的.在Meme理论中，meme作为文化的基本单位，通过模仿学习而传播，并代代相传.在这个过程中，每个个体通过meme的传递进行学习和自我调整，提高自身的竞争力[13].针对网络权值的确定问题是一个多维的优化问题,笔者提出了改进的粒子群算法作为全局搜索策略和改进的模拟退火算法作为局部搜索策略的文化基因算法.粒子群算法具有执行效率高等优点，模拟退火算法具有能使搜索跳出局部最优，并以较大概率取得全局最优解，具有较强的鲁棒性、全局收敛性等优点.笔者选取粒子群算法作为全局搜索策略，在搜索过程中，利用模拟退火算法对每次迭代过程中产生的群体极值进行局部退火搜索.这种协调方式即提高了搜索的效率又提高了搜索的精度.粒子群算法的基本原理源于对鸟群捕食行为的仿真.模拟退火算法(simulated annealing，简称SA)是随机的从某一较高初温出发，随着温度参数的不断下降,又结合了概率突跳特性，即在局部最优解处能概率性地跳出，并最终趋于全局最优.

(2)

模拟退火算法通过降温来进行循环迭代，即

(3)

其中：α为衰减因子.

当温度达到预定的终止温度时，此时得到的最优解代替全局的最优解，进行下一次的迭代，直至迭代结束.笔者文中引入了收缩因子s[14-15],可以有效地避免在搜索过程中陷入局部最优,得到

其中：φ=c1+c2；φ=c1+c2；i=1，2，…，N；j为微粒的第j维；k为迭代次数；c1,c2为加速常数；r1，r2为两个相互独立的随机函数.

笔者在传统的模拟退火算法的基础上中设置一个储存记忆器，用于保存每次迭代的最优解，最后选用min指令，找到储存记忆器中最优解中的最优.如下公式

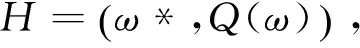
其中：ω*为退火过程中目标函数确定的最优解，Q(ω)为目标函数值.

3 MA优化的Chebyshev神经网络预测模型构造

(4)

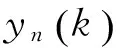
基于MA优化的Chebyshev神经网络的非线性动态系统预测，具体实现步骤如下

Step 1 确定Chebyshev神经网络动态模型的规模，选取合适的结构；

Step 2 种群初始化，设置各参数；

Step 3 将每个粒子对应的权值带入神经网络模型，计算粒子的适应度值即预测模型的输出与目标输出的误差，记录个体极值和群体极值；

Step 4 粒子群算法进行全局搜索，更新粒子的速度和方向，记录个体极值和群体极值；

Step 5 对每次迭代结果，利用模拟退火算法对群体极值进行局部搜索，记录个体极值和群体极值；

Step 6 更新粒子，达到指定的迭代次数，继续，否则转回Step 3，继续；

Step 7 当达到迭代次数时，从中选取最大适应度粒子，将该粒子对应的权值认定为最佳权值；

Step 8 执行Chebyshev神经网络模型对非线性系统的预测；

Step 9 结束.

建模流程图如图2所示.

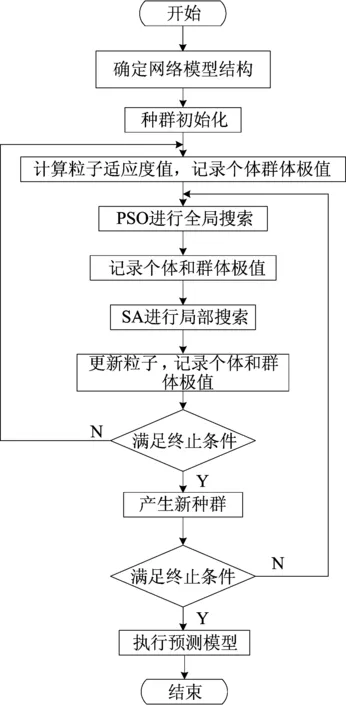
图2 流程图Fig.2 The flow chart

4 实验仿真与分析

确定选用2*5*1的Chebyshev神经网络动态模型，MA设置参数：初始温度100，温度下降系数0.8，MARKOV链长100，终止温度0.01，粒子数目80，迭代次数200，收缩因子s=0.7，加速因子c1=c2=1.49.为了比较方便，BP神经网络和PSO，SA都设置同样的参数.利用基于MA优化的Chebyshev神经网络预测模型和BP神经网络模型对非线性动态系统进行预测，确定的权值为

c=[0.264 0;0.226 7;0.257 5;0.174 2;0.276 5],

得到的预测值输出和实际输出结果如图3所示.

Chebyshev神经网络的预测值与实际输出值的误差值如图4所示，BP神经网络的预测值与实际输出值的误差如图5所示，预测结果曲线如图6所示.

图3 预测结果图Fig.3 The predicted results figure

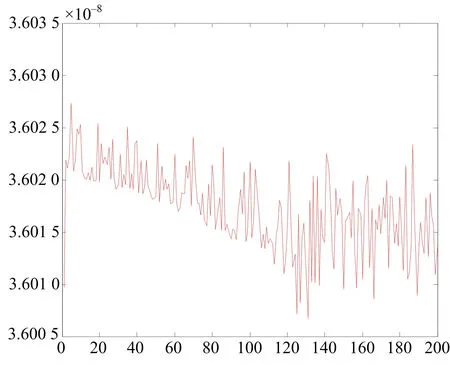
图4 Chebyshev网络预测误差图Fig.4 The prediction error of Chebyshev network

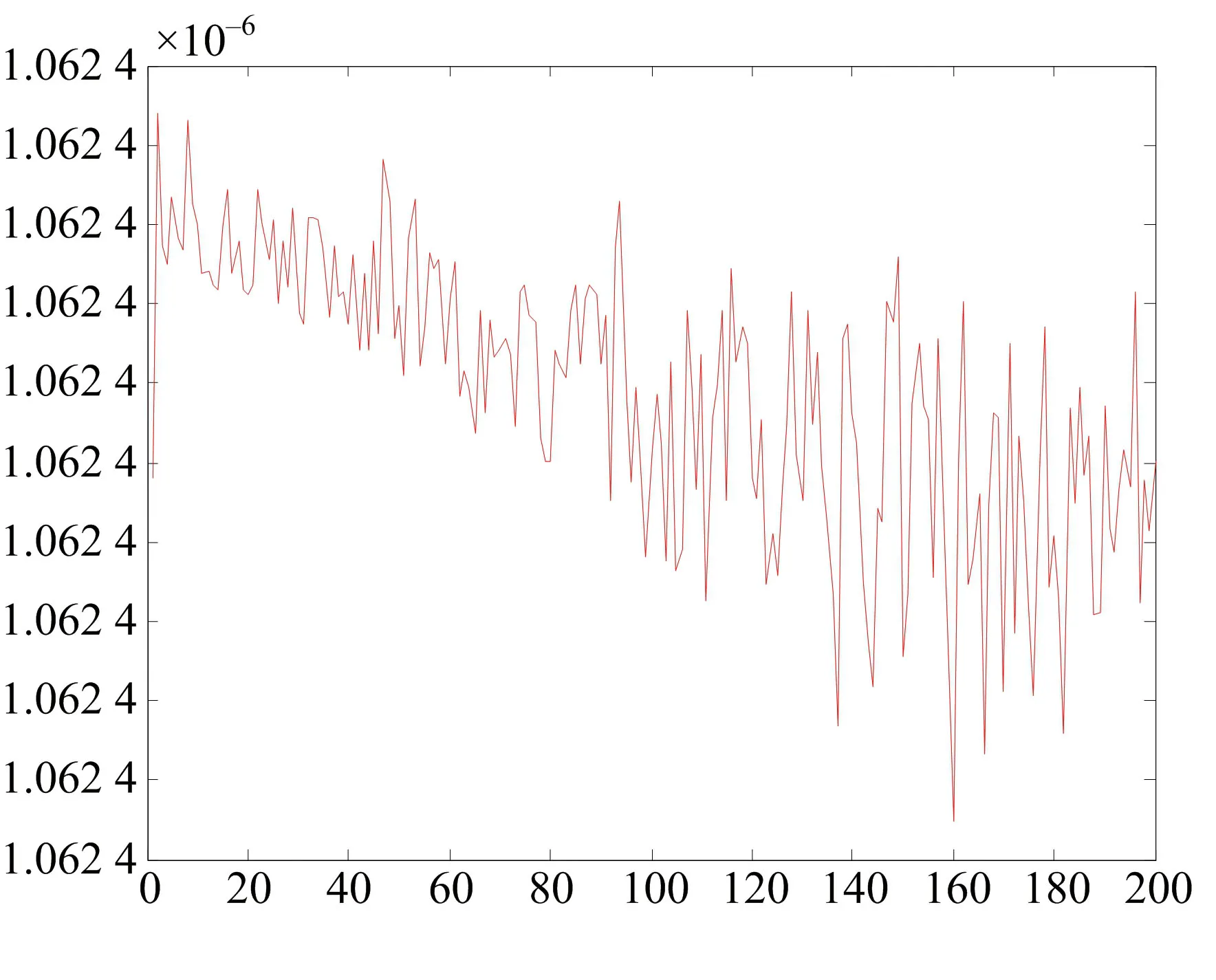
图5 BP网络预测误差图Fig.5 The prediction error of BP network

图6 预测结果比较图Fig.6 The comparison of the predicted results

由图3可以看出，Chebyshev神经网络预测模型的预测值与实际输出值拟合得较好，基本达到了全部一致，而基于MA优化的BP神经网络的预测值有部分点不能很好地与实际输出达到一致，表明了基于MA优化的Chebyshev神经网络与BP网络相比，具有更好的预测精度.从图4、5可以看出，Chebyshev神经网络对非线性动态系统的预测绝对误差可达到10-8，而BP神经网络对非线性动态系统的预测绝对误差为10-6，表明Chebyshev神经网络具有更高的预测精度和稳定性.

采用不同的算法优化Chebyshev神经网络预测模型的权值，可得到如图6所示的预测结果曲线.由图6可以看到，基于MA优化的预测结果精度要高于PSO和SA优化的预测模型，表明MA算法具有更好的优化效果.

5 结束语

笔者提出了一种以Chebyshev基函数作为隐层神经元激励函数，并使用以改进粒子群算法为全局搜索策略，改进模拟退火算法为局部搜索策略的文化基因算法来确定权值，克服了BP神经网络权值难以选取、迭代过程长、易陷入局部最优等缺点.仿真结果表明，基于MA优化的Chebyshev神经网络能在预测非线性动态系统时达到满意的预测效果，其泛化性能和预测能力远远优于BP神经网络.文化基因算法通过并行算法和串行算法的结合，将权值的确定问题转化为优化问题，使极值的确定更为精确，减少了Chebyshev神经网络的学习次数，使工作量大大减少.

[1] 穆朝絮,张瑞民,孙长银.基于粒子群优化的非线性系统最小二乘支持向量机预测控制方法[J].控制理论与应用,2010,2:164-168.

[2] 冯玮,曹继昌,吴舒婷,等.应用BP神经网络预测精锻斜齿轮损伤因子[J].武汉理工大学学报(信息与管理工程版),2014,3:328-331.

[3] 董世超.基于ARIMA-BP神经网络模型海流流速预测研究[J].中国科技信息,2014,2:86-88.

[4] 侯越.基于改进T-S模糊神经网络的交通流量预测[J].计算机科学与探索,2014,1:121-126.

[5] 周叙国,王伟.基于自适应PSO优化的空燃比神经网络预测控制[J].西南师范大学学报 (自然科学版),2014,5:64-68.

[6] 邹阿金,沈洪远.Chebyshev神经网络辨识器[J] .煤矿自动化,1998,4:9-10.

[7] 王宏伟,于双和.基于Chebyshev正交函数神经网络的混沌系统鲁棒自适应同步[J].控制理论与应用,2009,10:1100-1104.

[8] FRASER G,ARCURI A,MCMINN P.A memetic algorithm for whole test suite generation[J].Journal of Systems and Software,2015,103:311-327.

[9] HARRIS M,BERRETTA R,INOSTROZA-PONTA M,et al.A memetic algorithm for the quadraticassignment problem with parallel local search[C]//Evolutionary Computation (CEC),2015 IEEE Congress on IEEE,2015:838-845.

[10] MALL S,CHAKRAVERTY S.Numerical solution of nonlinear singular initial value problems of Emden-Fowler type using Chebyshev neural network method[J].Neurocomputing,2015,149:975-982.

[11] ZOU A,ZHANG S,TANG Y,et al.Anti-counterfeit algorithm based on Chebyshev chaotic neural networks[J].Chaos,2015,1 (4):1.

[12] 邹阿金,沈建中.基于Chebyshev神经网络的非线性预测应用研究[J].计算机应用,2001,4:14-15.

[13] 段海滨，张祥银，徐春芳.仿生智能计算[M].北京:科学出版社,2011.

[14] 宋莉莉,张宏立.应用改进粒子群算法辨识Hammerstein模型[J].计算机仿真，2013,3:269-272.

[15] KENNEDY J，EBERHART R C． Particle swarm optimization[C]// International Conferention Neural Networks，Perth，Australia，IEEE，1995:1942-1948．

(责任编辑 朱夜明)

The prediction of nonlinear dynamic system based on Chebyshev neural networks

LI Zhe

(Center of Network and Information Technology,Xinjiang University,Urumqi 830046,China)

For prediction of nonlinear dynamic systems is often affected by noise or coupling of other process,so the regularity is difficult to find.This paper put forward a set of Chebyshev orthogonal basis functions,as the excitation function of hidden neurons in neural networks,and constructed a new type of Chebyshev basis function neural network prediction model.This model was used as the nonlinear dynamic system prediction models,and optimized the weights of neural network by the memetic algorithm based on particle swarm optimization and simulated annealing algorithm.This method could achieve high prediction precision and good prediction results.Chebyshev neural network greatly reduced the workload,sped up the convergence than the traditional BP neural network.When compared with simulated annealing optimization or particle swarm optimization Chebyshev neural network,Chebyshev of memetic algorithm,when it was used to determine the weights of the neural network,had better fitting effect.

Chebyshev neural network;nonlinear dynamic systems;memetic algorithm;prediction

10.3969/j.issn.1000-2162.2016.06.007

2015-05-16

国家自然科学基金资助项目(51575469)

李 喆(1976-)，女，江苏泰州人，新疆大学讲师.

TP39

A

1000-2162(2016)06-0031-06