论柯西不等式在高中数学中的应用

甘肃省靖远县第一中学　石福禄

论柯西不等式在高中数学中的应用

甘肃省靖远县第一中学石福禄

柯西不等式是数学中一个非常重要的不等式，在代数、几何等方面应用非常广泛，常常被当做解题基础，可以利用条件快速得出结论。若能够灵活运用柯西不等式，可以使一些问题巧妙地得以解决，我们要适当地构造使用它的条件，以达到最终目的。

柯西不等式；变式；应用

一、柯西不等式的主要变形公式

柯西不等式有多种变形，已经成为现在许多数学理论的出发点。掌握几种常见的柯西不等式的变形，能够让我们对柯西不等式有更全面的认识，在解决数学问题时，也可以快速使用合适的变形形式解题。以下列举常见的几种柯西不等式的变形形式：

二、利用不同的变形方法解决问题：

下面举例说明如何根据题目选择柯西不等式的变形形式来解决问题，即柯西不等式的变形技巧。

1.等价变形

将要解决的不等式问题作等价变化，构造出n个实数的平方和与另n个实数平方和的乘积的形式。

2.换元求解

有时根据所证不等式的结构特征，适当换元，可以转化成为容易应用柯西不等式的结构特征，快速解决问题。

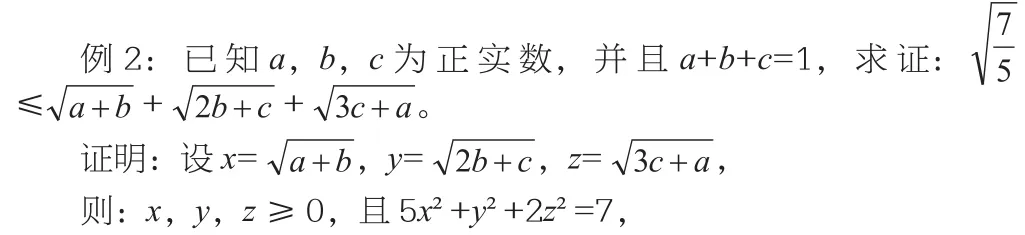
由柯西不等式，得：

三、柯西不等式的应用

1.解决距离问题

证明：取直线上的任意一点Q（x，y），得Ax+By=-C，且A²+B²≠0。

由柯西不等式得：

2.证明等式和不等式

在等式问题上，可以探索出新的方法，另辟蹊径。柯西不等式既然含有等号，就可以用来解决等式问题。同时利用不等式来解决等式问题，可以让我们深刻领会到等式和不等式之间的相通性，培养辩证思维。

例4：已知正数a，b，c满足a+b+c=1，

总之，柯西不等式形式多变，为我们解决高中的数学问题提供了极大的便利。深刻认识柯西不等式的定义并且能够掌握其变式，灵活运用到解决问题的过程中，将对我们在高中阶段的数学学习有很大的帮助。

［1］姚允龙.数学分析［M］.第二版，上海复旦大学出版社，2007.

［2］斐礼文.数学分析中的典型解题方法［M］.第二版，北京高等教育出版社，2006.

［3］蔡玉书.系列讲座之八——柯西不等式［J］.中学数学月刊，2010.