基于特征分解谱估计的蓄电池内阻检测方法

唐骏宇，冯长江

(军械工程学院，石家庄 050003)



基于特征分解谱估计的蓄电池内阻检测方法

唐骏宇，冯长江

(军械工程学院，石家庄 050003)

针对目前在蓄电池内阻检测中被广泛采用的锁相放大法存在硬件电路复杂、成本较高、操作复杂等问题，提出采用特征分解谱估计的方法来替代蓄电池内阻检测中的锁相放大环节，以软件计算的方法替代硬件电路，从而降低硬件成本及操作难度；通过对特征分解谱估计的原理分析以及对运用特征分解谱估计方法进行蓄电池内阻测量时的关键步骤，即电压信号的提取与幅值检测进行仿真，仿真表明特征分解谱估计方法在高功率噪声背景下仍有较高的频率分辨力，幅值测量结果在50dB高斯白噪声背景下测量误差约为2%，而在20dB非高斯白噪声背景下测量误差约为3%；分析表明基于特征分解谱估计的蓄电池内阻检测方法在较高功率非高斯噪声背景下具有良好的检测效果，可以作为微弱信号检测的软件实现方法以替代锁相放大环节。

现代信号处理；特征分解法；功率谱估计；蓄电池内阻检测

0 引言

蓄电池作为电源系统的备用电源，已广泛应用于工业生产、交通、通信等行业。如果电池失效或容量不足，就有可能造成重大事故，所以，对蓄电池的运行参数进行全面地在线监测，对提高直流系统的安全运行、提高供电系统的可靠性和自动化程度都有着十分重要的意义。蓄电池的内阻是蓄电池的一个非常重要的性能参数，它可以作为计算推断蓄电池的其他各项性能指标(如剩余电量、健康状况等)的主要依据。然而蓄电池的内阻很小，一般为毫欧级别，这使得对其进行测量时，消除噪声和外界干扰的影响、提高测量精度显得尤为重要。目前对蓄电池内阻的测量中多采用锁相放大技术来完成对蓄电池内阻测量信号的提取。锁相放大技术是一种基于硬件电路的微弱信号检测技术，主要基于相干检测技术实现对信号的提取，研究表明锁相放大技术运用于蓄电池内阻检测可以取得良好的检测效果，但锁相放大器内部结构复杂，成本高昂，并且锁相放大技术检测电压时对参考信号与待测信号相位的一致性有很高的要求，需要复杂的调节操作过程[1]，上述这些都是运用锁相放大技术的蓄电池检测设备推广的阻碍。采用基于现代信号处理的信号检测方法可以用软件替代蓄电池检测中的锁相放大环节，降低硬件成本并简化操作。

1 采用交流法的蓄电池内阻检测一般步骤

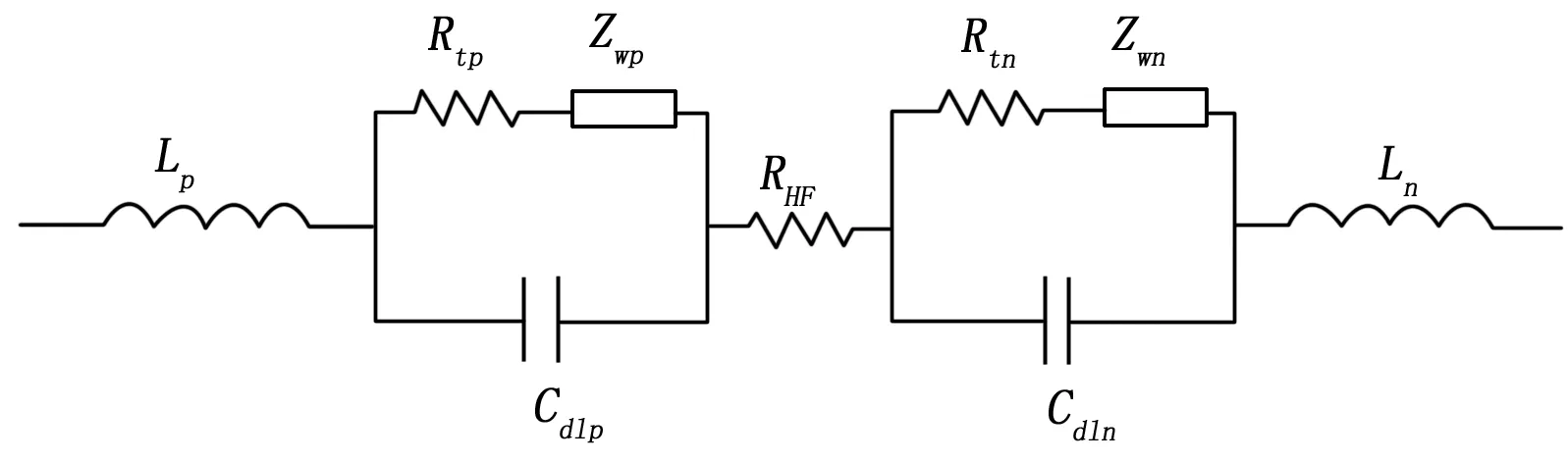
图1 蓄电池内阻等效模型

交流注入法适用于蓄电池内阻的在线检测，其主要方法是检测系统给蓄电池一个已知频率的交流电流信号，而后检测蓄电池两端的电压，这样就可以计算出电池的内阻。蓄电池内阻抗等效模型如图1所示[2]：Lp、Ln是电池正负极电感，Rtp和Rtn是电极离子迁移电阻；Cdlp和Cdln是电极双电层电容；Zwp和Zwn为Warburg阻抗，是由离子在电解液和多孔电极中扩散速度决定的；RHF为欧姆内阻，包括蓄电池内部的电极、隔膜、电解液、连接条和极柱等全部零部件的电阻。电池的欧姆内阻能反映出电池的性能状态，因此对电池内阻的测量多指测量电池的欧姆内阻。

典型的铅酸蓄电池阻抗谱如图2所示[2-3]。

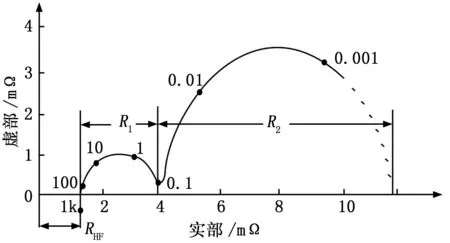
图2 铅酸蓄电池阻抗谱

可以看到，在频率高于100 Hz而低于1 kHz时，蓄电池的阻抗谱近似平行于Y轴，此时蓄电池阻抗的实部几乎不变，其大小即是蓄电池的欧姆内阻Rhf。因此可以在100 Hz～1 kHz之间由低到高进行扫频测量，所测得蓄电池内阻抗的最小值即为蓄电池的欧姆内阻。设激励电流信号：

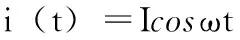
(1)

则响应电压信号为：

(2)

所得内阻抗幅值可以计算得出：

(3)

蓄电池内阻检测过程中的待测信号通常包含有用的与已知电流信号频率相同的交流电压信号、噪声信号和干扰信号。其中噪声信号一般为环境、仪器引入的噪声和蓄电池本身的噪声，而干扰信号包括工频干扰和在线检测时充电器产生的纹波电压干扰。蓄电池内阻检测系统的核心任务就是从噪声和各种干扰中提取出有用的电压信号，通过对电压信号的分析计算得到电池的内阻。

2 特征分解谱估计

噪声和干扰的存在使得待测信号随时间的变化没有明确的变化规律，对这样的信号进行采样之后形成了一个时域离散随机信号(随机序列)。对于离散随机信号的了解是通过对其自相关函数以及功率谱进行估计来完成的。对于蓄电池内阻检测中的待测电压信号，我们所关心的是其所含频率分量以及各频率分量的幅值。基于信号自相关矩阵的特征分解谱估计充分考虑了信号的已知特性，它将样本空间分成信号子空间和噪声子空间两部分，一旦确定了这些子空间，就可以用一个频率估计函数来估计信号谱中包含的频率值，而后再确定每个频率值所对应的幅值和功率[4]。

设经过采样后的随机序列x(n)为白噪声与多个复指数分量之和：

(4)

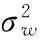
(5)

其中：Pi=|Ai|2是第i个复指数分量的功率，ωi与Ai均为未知。

x(n)的M×M阶自相关阵可表示为信号的自相关阵Rs和噪声的自相关阵Rn，即：

(6)

其中：第i个分量的信号自相关矩阵Rsi的具体形式为：

(7)

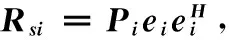
(8)

(9)

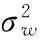
(10)

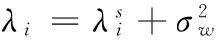
Ps=VsVsH，Pn=VnVnH

(11)

对复指数频率的估计有多种方法，本文采用多重信号分类(MUSIC)算法[3]，其频率估计函数为：

(12)

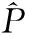
确定复指数频率后，各频率对应的功率可通过解如下方程组得出：

(13)

其中:Vi(ejωk)是频率ωk处信号子空间特征向量vi的DTFT，即：

(14)

λi是vi所对应的特征值。

在实际的检测过程中，实际信号的自相关函数一般难以精确得出，因此需要通过有限长的采样序列来对其进行估计，采用的估计方法[1，4]如式(15)所示：

(15)

其中:N为采样序列长度。

通过以上分析，可以得出基于特征分解谱估计的蓄电池内阻检测步骤：

1) 给予电池100Hz的交流电流激励，通过交流四线制测量方法[1,5](如图3)引入待测信号；

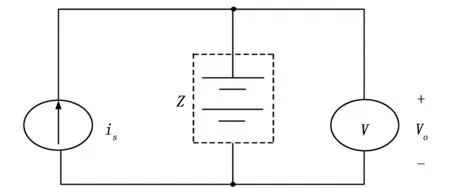
图3 交流四线制测量法

2) 对待测信号进行采样、A/D转换，形成待测随机序列；

3) 截取待测随机序列的有限长度，根据式(15)对序列自相关函数进行估计，并计算形成自相关矩阵；

4) 求解自相关矩阵的特征值，其中最小特征值对应的特征向量形成噪声子空间Vn；

5) 根据式(12)求解PMN的极大值，各极大值对应的频率即为待测信号所含频率其中与激励频率相等或相近的频率分量即为需要提取的信号分量(响应信号分量)；

6) 将所得频率代入式(13)解方程，可以得到各频率分量的功率，进而求得其幅值；

7) 根据式(3)，响应信号分量的幅值除以激励信号幅值即可得到蓄电池的内阻抗值；

8) 增加激励频率，所加步长根据所需测量精度而定，重复步骤1)～7)，并用此次测量结果与上次比较，若此次结果小于上次，则取内阻值为两次结果的平均值，结束测量。

值得注意的是，特征分解谱估计得出的频率分量是指复频率分量，因而一个实际的正弦信号分量对应的是正负两个复频率分量，即：

(16)

所以在计算功率时应考虑这一点，正负两个复频率分量功率之和才是原正弦信号分量的功率。

3 蓄电池内阻检测仿真分析

由于蓄电池内阻检测系统的核心任务就是从噪声和各种干扰中提取出有用的电压信号，通过对电压信号的分析计算得到电池的内阻，所以对蓄电池内阻检测的仿真主要是对检测信号的提取及测量的仿真。

构造蓄电池内阻检测中的电压信号，其幅值为U，频率为f。在此信号上叠加高斯白噪声作为测量噪声，最终形成待测原始信号：

u(t)=Ucos2πft+w(t)

(17)

取所测电压信号U=200mV，f=100Hz，则有：

u(t)=200cos2000πt+w(t)

(18)

分别叠加功率为5dB、10dB、20dB、50dB噪声，形成的原始信号如图4所示。

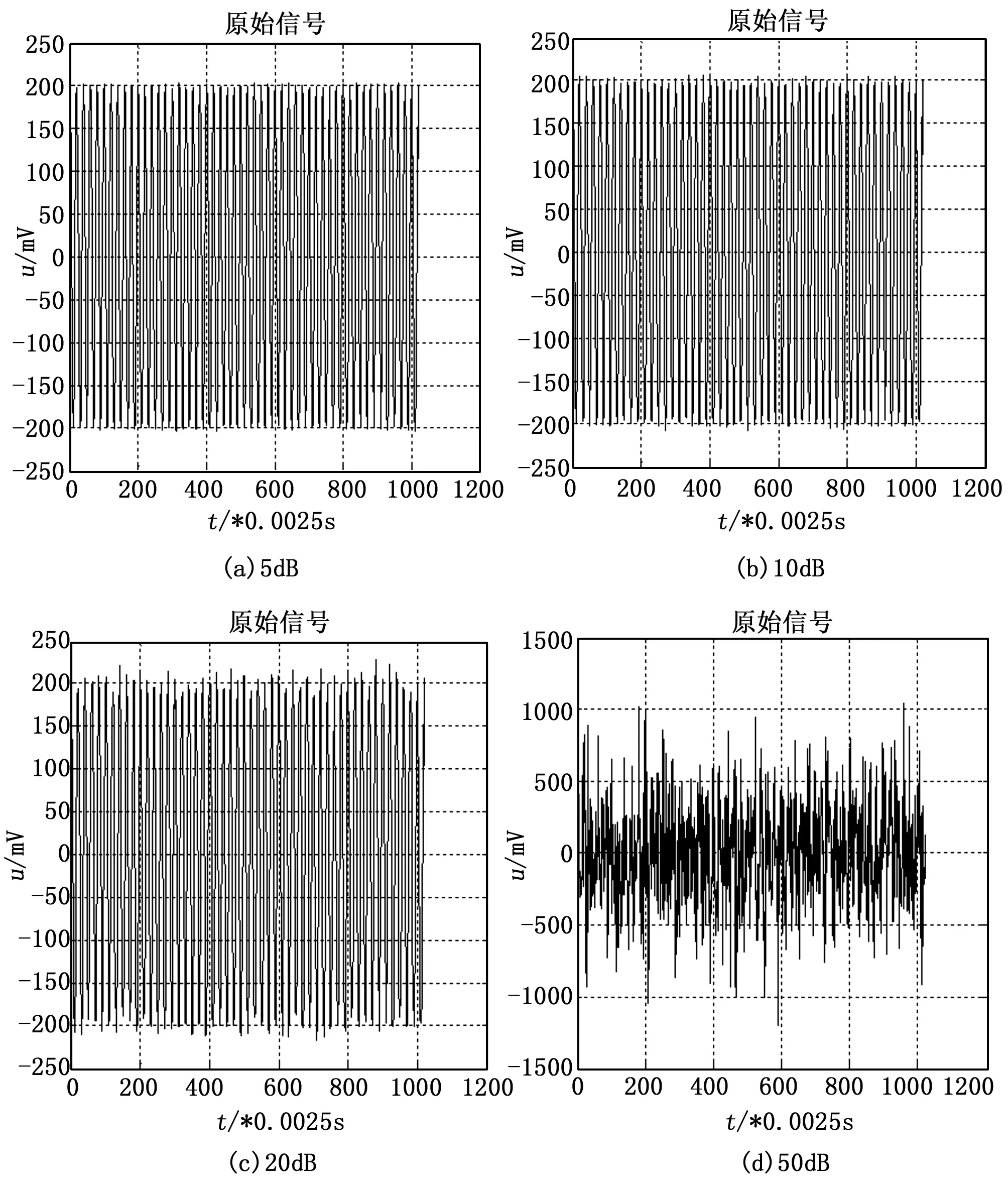
图4 加入不同功率的噪声形成原始信号

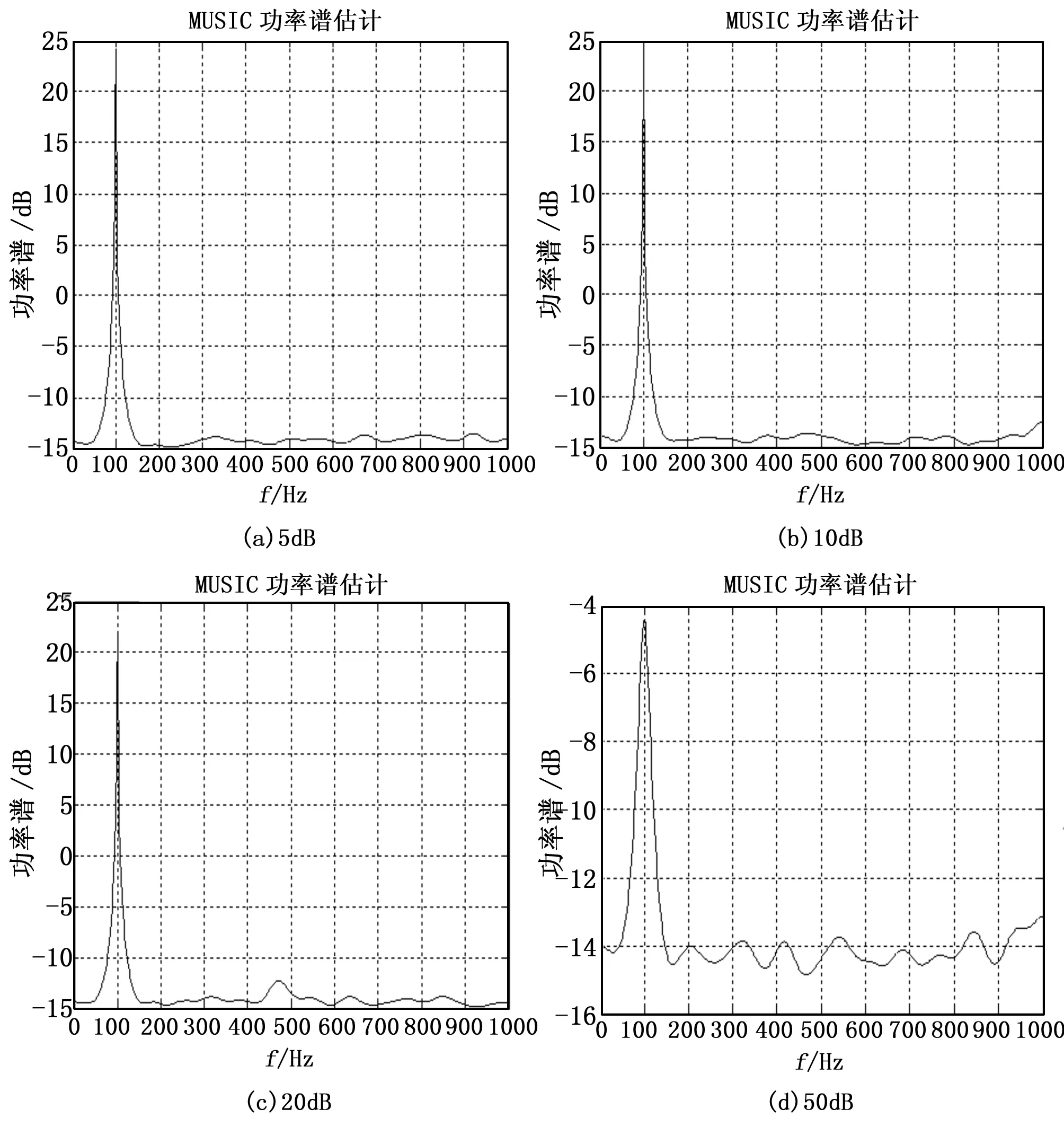
图5 不同噪声背景下功率谱估计结果

对上述原始信号进行特征分解机谱估计，采样频率为2 000Hz，结果如图5所示。

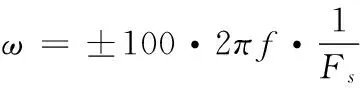
(19)

事实上方程组中的两个方程是等价的，只需一个方程即可解出功率P：

(20)

对上述不同噪声背景下的信号进行幅值检测得到如表1所示结果。

表1 不同噪声功率背景下幅值检测结果

以上仿真假定所含噪声为高斯白噪声，若检测过程中只存在环境以及仪器产生的热噪声，则上述仿真数据是有意义的。但实际上待测原始信号中所含并非高斯白噪声，而是包括工频干扰、纹波干扰等各种干扰信号所叠加而成的非高斯噪声。假设原始信号中包括50Hz工频干扰、300Hz高次谐波，由于激励信号频率已知为100Hz，因此可以把其他频率成分都看做噪声，它们与属于白噪声的热噪声叠加形成非高斯噪声，即：

u(t)=Ucos2πft+w(t)

(21)

w(t)=U1cos2πf1t+U2cos2πf2t+w0(t)

(22)

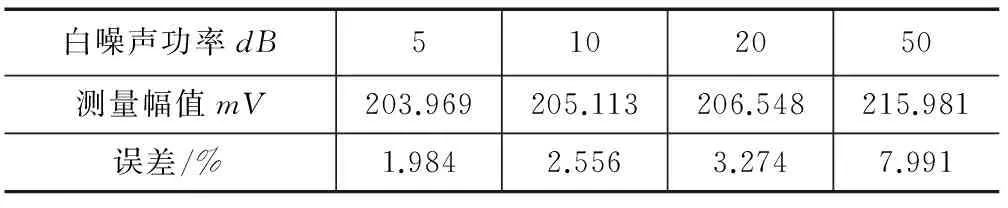
其中:w0(t)为高斯白噪声，U=200mV，U1=10mV，U2=50mV，f1=50Hz，f2=300Hz,白噪声功率分别取5dB、10dB、20dB、50dB，然后对其进行谱估计，得到功率谱图及幅值预测值如图6和表2所示。

白噪声功率dB5102050测量幅值mV203.969205.113206.548215.981误差/%1.9842.5563.2747.991

可以看出，在非高斯噪声背景下，基于特征分解谱估计的频率检测无法分辨出50Hz的工频干扰，而对100Hz电压信

号以及300Hz的高次谐波具有良好的分辨力；幅值检测误差有所增加，但在白噪声功率为20dB以下时的测量误差仍然在可接受范围之内。

4 结论

采用特征分解谱估计对蓄电池内阻进行检测，能在较强的噪声背景下提取出所需的电压响应信号，然而该方法无法分辨工频干扰，并且检测过程中引入的工频干扰、纹波干扰等非白噪声干扰对最终的幅值检测结果有一定影响，因而在使用该方法进行检测时仍然需要滤波环节，但使用该方法可以降低对滤波性能的要求。特征分解谱估计方法使用软件算法代替了锁相放大法所需的硬件环节，可以简化系统的硬件结构，降低检测系统的硬件成本。

[1] 田 蕊.基于现代信号处理的铅酸蓄电池内阻检测[D]. 北京：北京交通大学，2014.

[2] 邓 颖.基于模糊控制的通信电源蓄电池监测系统的设计与研究[D]. 武汉：武汉理工大学，2008.

[3] 卢小泉，薛中华，刘秀辉.电化学分析仪器[M]. 北京：化学工业出版社，2010.

[4] 王炳和.现代数字信号处理[M]. 西安：西安电子科技大学出版社，2011.

[5] 李运涛，曹建刚，董志强,等.蓄电池内阻检测方法研究与实现[J]. 火炮发射与控制学报，2012(4)：59-62.

Battery Resistance Detection based on Eigendecomposition Spectrum Estimation

Tang Junyu, Feng Changjiang

(Ordnance Engineering College, Shijiazhuang 050003，China)

Method based on eigendecomposition spectrum estimation is used to replace lock-in amplifier which is widely used in battery resistance detection. The new method can reduce hardware costs and operational difficulties due to use software way instead of hardware circuit. Series analyses about the theory of eigendecomposition spectrum estimation are taken. Simulations about the extraction and measuring for voltage signal,which is the key step in the method, are done in the paper. Results of simulations shows good frequency resolution. The measurement error of the method can be around 2% under 50dB white Gaussian noise, while around 3% under 20dB non-Gaussian noise background. Analysis and simulations shows the method based on eigendecomposition spectrum estimation is efective in battery resistance detection under higher power non-Gaussian noise background and can be software method of Weak Signal Detection to replace lock-in amplifier.

modern signal processing; eigendecomposition; spectrum estimation; battery resistance detection

2015-11-17；

2015-12-24。

唐骏宇(1992-)，男，湖南益阳人，硕士研究生，主要从事电气测试技术与智能系统方向的研究。

冯长江(1963-)，男，河北石家庄人，教授，硕士生导师，主要从事电气测试技术与智能系统方向的研究。

1671-4598(2016)06-0037-04DOI：10.16526/j.cnki.11-4762/tp

TP

A