基于验前试验信息熵的测试性验证试验方案

吴忠德，邓 露

(1.海军航空工程学院 飞行器检测与应用研究所，烟台 山东 264001；2.92074部队，浙江 宁波 315000)



基于验前试验信息熵的测试性验证试验方案

吴忠德1，邓 露2

(1.海军航空工程学院 飞行器检测与应用研究所，烟台 山东 264001；2.92074部队，浙江 宁波 315000)

产品在研制阶段存在大量的试验数据，为有效利用验前数据，降低测试性验证试验样本量，提出一种基于验前试验信息熵的测试性验证试验方案。该方案利用信息熵来度量研制阶段多次验前试验数据对测试性验证试验所起的作用，依据平均互信息熵和信息总量相等的原则，将多次验前试验数据等效成一次成败型数据；在此基础上，通过相容性检验方法确定验前数据与试验数据的相容性水平，并以Beta分布为验前分布，利用加权混合贝叶斯理论建立混合验后分布，之后，基于贝叶斯平均风险理论求解满足双方风险要求的试验方案；最后，以某型雷达发射分机为例，对其进行测试性验证试验研究，研究结果验证了该方案的有效性。

测试性验证试验；信息熵；相容性检验；Beta分布

0 引言

测试性验证试验是通过注入一定数量的故障模式来检验被测单元的机内测试或者外部测试的故障诊断能力[1]，即在综合考虑承制方和使用方的利益以及试验费用等诸多因素的基础上，利用“一次抽样检验”或“序贯抽样检验”方法，确定故障样本量以及允许的最大故障诊断失败次数，通过测试性验证试验来验证产品的测试性指标是否满足设计要求[2-4]。对测试性验证试验方案的确定一般采用MIL-STD-471A通告2的方法[5]、ADA081128报告的方法[6]、国军标GJB2072-94的方法等[7]。周玉芬等[8]在总结国内外测试性试验验证中的关于试验样本量和结果判定方法的基础上，得出二项分布法和泊松分布具有明显优势的结论。田仲教授[9]以二项分布检验模型为基础，确定了测试性验证试验方案。石君友等[10-11]建立了故障样本集的信息充分覆盖准则，并依此准则给出了确定测试性验证试验方案的方法。文献[12-13]提出了成败型产品的Bayes验证试验方案，利用验前信息制定可靠性验证试验方案，减少了样本量。李进等[14]提出基于决策级数据融合的可靠性综合验证试验方法，利用证据组合理论融合专家信息、评估信息和试验信息，达到了减少试验样本量的目的。在可靠性验证试验研究的基础上，李天梅等[15-16]提出利用研制阶段试验数据制定测试性验证试验方案的新方法，方法通过引入折合因子，将验前数据等效成试验数据。常春贺等[17]提出基于研制信息的测试性验证试验方案，方案基于证据组合理论融合研制阶段的多种信息。

1 成败型定数抽样检验方案

典型的成败型试验定数抽样检验方案的思路如下：随机抽取n个样本进行试验，其中有f个失败。规定一个正整数c，如果f≤c，则认为合格，判定接收；如果f>c，则认为不合格，判定拒收。c为合格判定数，试验方案记为(n,c)。

设产品失败的概率为p，则在n次试验中，出现f次失败的概率为:

(1)

接收的概率即是n个试验样本中失败次数小于等于c的概率，亦即失败次数为0，1，2，…，c的概率总和。显然，接收概率L(p)与p有关，L(p)可记为:

(2)

则拒收概率为:

(3)

使用方根据需要选定一个极限水平，与之对应的是一个低的接收概率，低于接收概率的不予以接收。当质量水平为极限质量时的接收概率叫“使用方风险”，记为β。β一般可取0.1，0.2或其他值。给定极限质量p1，对应L(p1)=β，则当p>p1时，接收概率不高于β。显然，对于生产方，也存在一个“生产方风险”，记为α，表达当产品达到设计指标p0时被拒绝的概率，一般取α=β。当生产方选定p0时，则L(p0)=1-α，即以大概率接收。

因此，当生产方和使用方协商确定p0，p1和对应的α，β后，就可以通过下式确定试验方案，即求出正整数n和

(4)

令q=1-p，由于n和c只能是正整数，正好满足上述等式的正整数不一定存在，所以应求满足下式的最小n和c值，即是要求的试验方案。

(5)

显然，当对产品的FDR/FIR要求较高及双方风险要求较低时，由式(5)确定的故障样本较大。例如规定的q0=0.95，q1=0.90，α=β=5%，则确定的试验方案为(298,21)，即需要注入298个故障，如果试验失败的次数不大于21，则产品合格，予以接受，反之，则不合格，拒收。

在实际工程中，鉴于故障注入具有破坏性，对验证产品注入如此大量的故障往往难以实现。例如，对飞行器类装备，在验证试验时注入298个故障是不现实的，若采用减少样本量的方案(46,1)，则使用方的风险为4.8%，生产方的风险为67.68%，是一个生产方难以承受的验证试验方案。

2 验前试验数据信息熵等效分析

2.1 熵的基本定义

熵是随机试验结果不确定性的度量，一般也称信息熵。关于熵的定义有多种，本文以Shannon信息熵理论为基础，对离散形式的验前试验数据进行信息量分析。设将信源X看作随机变量，X的概率为P(X)，则信源X的熵的定义为:

(6)

式中，H(X)表示信源X的不确定度。下文将利用信息熵理论确定验前试验数据的不确定度，并将不同阶段的多次试验数据等效成一次成败型试验。

2.2 验前试验数据信息熵等效分析

假设产品在研制期间共进行了N次测试性摸底或增长试验，第i次试验的结果为(ni,ci)，其中ni为第i次试验故障注入的数量，ci为第i次试验故障诊断失败的次数。第i次试验提供成功的信息的概率为pi，提供失败的信息的概率为1-pi，则第i次试验提供的平均互信息量为：Hi=-pilnpi-(1-pi)ln(1-pi)

(7)

显然，第i次试验总的信息量为niHi。

对于研制阶段的N次测试性摸底试验，由于不同阶段的平均互信息量不同，其对消除产品测试性不确定性所作的作用不同，因此可以依据各阶段试验的平均互信息量确定融合权重，定义为:

(8)

则N次试验的加权互信息量为:

(9)

设成败型等效试验为(n0,c0)，其中，n0为抽样试验的次数，c0为试验失败的次数，则等效试验提供成功的概率为p0，提供失败的概率为1-p0。等效试验提供的平均互信息量为:

(10)

(11)

同时，根据信息总量相等的原则和式(11)可得:

(12)

3 试验方案制定

3.1 基于Bayes理论混合验前分布分析方法

对于成败型试验数据，取测试性指标q的无信息验前分布为：

(13)

利用上节确定的成败型等效试验数据，通过Bayes方法，可以得到无验前信息分布条件下的验后分布为:

(14)

将其作为验前分布，与无信息验前分布Beta(q;1,1)进行加权混合，得到混合验前分布为:

(15)

其中：ε为融合权重，其物理意义是反映验前数据与验证试验数据的相容性水平，ε的取值范围为0≤ε≤1，即当ε=0时，有π0(q)=1，表示验前信息与验证信息完全不相容；当ε=1时，有π0(q)=Beta(q;n0-c0+1,c0+1)，表示验前信息与试验信息完全相容。

设制定的测试性验证试验方案为(n,c)，根据得到的加权混合验前分布，经过推到可得到Bayes验后分布为:

(16)

式中，

(17)

验后融合权重为：

(18)

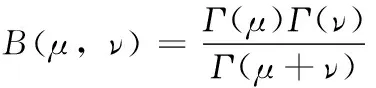
(19)

当ε=1时，有λ=1，表示验前信息与试验信息完全相容，则相应验后分布为

(20)

3.2 确定融合权重

对于验前信息的融合权重可以根据可信度或一致性水平获得，下面给出一种基于相容性检验确定验前信息可信度的方法。

设X为验证试验样本，Y为验前试验样本。为检验两个样本是否属于同一总体，进行如下检验假设：

(21)

(22)

因此，可以定义可信度为：在采纳H0的情况下，H0成立的概率，亦即X与Y属于同一总体的概率，记为P(H0|A)。由Bayes公式得:

(23)

式中，P(A|H0)=1-α，P(A|H1)等于H1为真时采纳了H0的概率，即为采伪的概率β。则样本X与样本Y的相容性水平为:

(24)

式中，P(H0)表示在获得验证试验样本之前H0成立的先验概率。

3.3 制定验证试验方案

假设合同规定的承制方风险为α0，使用方风险为β0，测试性最低可接受值为p1，目标值为p0。通过验前试验信息熵等效分析方法将多次验前试验数据等效成一次成败型试验方案为(n0,c0)，基于相容性检验确定验前信息可信度方法确定验前信息的融合权重为ε，则可以根据式(16)和(18)求得的加权混合验后分布。

(25)

设得到的加权混合验后分布为π(q;n0,c0,n,c)，则可以通过下式确定满足双方风险要求的试验方案(n,c)[18]。

4 案例应用及结果分析

4.1 案例应用

以某型机载雷达系统为对象，对其进行测试性验证试验研究。雷达系统作为机载设备的重要组成部分，主要作用是用于目标探测和跟踪。该雷达系统组成包括9个现场可跟换单元(LRU)，对其中的3个LRU进行测试性验证试验研究。3个LRU在研制阶段都共进行过3次测试性试验，3次试验的结果如表1所示。

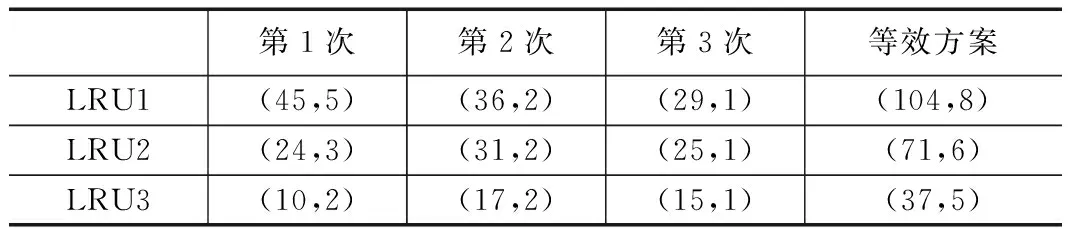
表1 研制阶段试验数据

通过验前试验信息熵等效分析方法分别将3个LRU在研制阶段的3次验前试验数据等效成一次成败型试验数据，结果为：LRU1验前试验数据等效为(104,8)；LRU2验前试验数据等效为(71,6)；LRU1验前试验数据等效为(37,5)。

经生产方和使用方协商确定LRU1的测试性指标q0=0.95，q1=0.90，生产方风险α=0.05，使用方风险β=0.05，按式(5)确定的标准抽样方案为(298,21)，即试验样本量为298，允许的最大失败次数为21。协商确定LRU2的测试性指标q0=0.95，q1=0.90，生产方风险α=0.1，使用方风险β=0.1，按式(5)确定的标准抽样方案为(187,13)，即试验样本量为187，允许的最大失败次数为13。协商确定LRU3的测试性指标q0=0.90，q1=0.80，生产方风险α=0.1，使用方风险β=0.1，按式(5)确定的标准抽样方案为(86,12)，即试验样本量为86，允许的最大失败次数为12。利用本文方法确定的测试性新验证试验方案如表2所示。

表2 标准抽样方案与新试验方案

4.2 结果分析

根据表2中求得的试验方案，可以得出以下几点结论。

1)由于LRU1的测试性指标要求高，生产方和使用方风险要求低，按照标准抽样方案得到的测试性验证试验方案为(298,21)。如果利用研制阶段的试验数据，在此基础上制定的测试性验证试验方案为(207,13)。在满足双方风险要求的情况下，试验所需的样本量减少了21%。

2)对于LRU2，按照标准抽样方案得到的测试性验证试验方案为(187,13)。如果利用研制阶段的试验数据，在此基础上制定的测试性验证试验方案为(128,7)。在满足双方风险要求的情况下，试验所需的样本量减少了32%。

3)对于LRU3，按照标准抽样方案得到的测试性验证试验方案为(86,12)。如果利用研制阶段的试验数据，在此基础上制定的测试性验证试验方案为(57,7)。在满足双方风险要求的情况下，试验所需的样本量减少了34%。

4)在不考虑研制阶段试验数据的情况下，如果采用新方案进行测试项验证试验，则对于LRU1，使用方承担的风险为15.69%；对于LRU2，使用方承担的风险为31.04%；对于LRU2，使用方承担的风险为20.66%。使用方承担的风险远高于合同要求。

5 结论

针对产品在研制阶段存在大量的试验数据的情况，提出了一种基于验前试验信息熵的测试性验证试验方案。该方案能有效降低测试性验证试验样本量，或在验证试验故障样本量保持不变的情况下降低风险。于技术复杂、造价高昂、风险要求低的武器装备利用本文方法能有效减少试验样本量大，缩短试验周期长，降低试验费用高。

[1] 田 仲，石君友. 系统测试性设计分析与验证[M]. 北京：北京航空航天大学出版社, 2003.

[2] 韩庆田, 卢洪义, 杨兴根. 军用装备测试性技术发展趋势分析[J]. 仪器仪表学报, 2006, 27(s6): 352-354.

[3] Laurent O. Using formal methods and testability concepts in the avionics systems validation and verification (V&V) process[A]. Proc. of 2010 Third International Conference on Software Testing, Verification and Validation[C]. 2010:1-10.

[4] 石君友，纪 超，李海伟. 测试性验证技术与应用技术现状分析[J]. 测控技术, 2012, 31(5):29-32.

[5] Department of Defense. MIL-STD-471A Maintainability verification/demonstration/evaluation[S]. U.S. Government Printing Office, 1973.

[6] Pliska T F, Angus J, Jew F L. ADA081128: BIT/external test figures of merit and demonstration techniques[R]. Rome Air Development Center Griffiss AFBNY, 1979.

[7] 国防科学技术工业委员会. GJB2072-94维修性试验与评定[M]. 北京: 中国标准出版社, 1994.

[8] 徐忠伟, 周玉芬, 高锡俊. 测试性验证中抽样方案的精确算法[J]. 空军工程大学学报：自然科学版, 2000, 11(1):76-78.

[9] 田 仲. 测试性验证方法研究[J]. 航空学报, 1995, 16: 65-70.

[10] 石君友, 康 锐. 基于通用充分性准则的测试性试验方案研究[J]. 航空学报, 2005, 26(6):691-695.

[11] 石君友, 田 仲. 机内测试定量要求的现场试验验证方法研究[J]. 航空学报, 2006, 27(5):883-887.

[12] 田艳梅, 张志华, 郭尚峰. 二项分布下的一种贝叶斯可靠性验收试验方案[J]. 运筹与管理, 2004, 13(4): 65-68.

[13] 张志华, 姜礼平. 成败型产品的Bayes鉴定试验方案研究[J]. 海军工程大学学报, 2004, 16(1): 9-13.

[14] 李 进, 赵 宇, 黄 敏. 基于决策级数据融合的可靠性综合验证方法[J]. 北京航空航天大学学报, 2010, 36(5): 576-579.

[15] 李天梅, 丘 静, 刘冠军. 利用研制阶段试验数据制定测试性验证试验方案新方法[J]. 机械工程学报, 2009, 45(8): 52-58.

[16] 李天梅, 丘 静, 刘冠军. 基于Bayes变动统计理论的测试性外场统计验证方案[J]. 航空学报, 2010, 31(2): 335-341.

[17] 常春贺, 杨江平, 曹鹏举. 基于研制信息的测试性验证试验方案研究[J]. 航空学报, 2012, 33(11): 2057-2064.

[18] Hamada M S, Wilson A G, Reese C S, et al. Bayesian reliability [M]. New York: Springer, 2008.

Method for Testability Demonstration Test Design Based on Entropy of Prior Test Information

Wu Zhongde1,Deng Lu2

(1.Research Institute of Aircraft Detection and Application , Naval Aeronautical Engineering Institute,Yantai 264001,China； 2.Unit 92074 of PLA,Ningbo 315000,China)

In the development stage, there is a large number of test data. Aiming to making good use of the prior test data and reducing the sample number of testability demonstration test, a method for testability demonstration test design based on information entropy of prior test information is proposed. In the method information entropy is used to check the role of different prior test data for the testability demonstration test, and many times prior test data is equivalent to success or failure data at a time according to the principles of equal mean interactive entropy and equal total information. On this basis, compatibility of prior data and test data is established by the method of compatibility test, while Beta distribution is made use as prior distribution and the mixed posteriori distribution is established by weighted hybrid Bayesian theory. Then, testing scheme satisfying the risk requirement of producer and consumer is solved based on Bayesian average risk theory. At last, to verify the proposed method, an example of a certain type of transmitter is given, and the result shows the validity of the proposed method.

testability demonstration test; information entropy; compatibility test; Beta distribution

2015-11-17；

2016-01-18。

总装武器装备预研基金(9410A27020212JB14311)。

吴忠德(1982-)，男，安徽安庆人，硕士研究生，主要从事测试性设计和验证方向的研究。

邓 露(1986-)，男，安徽芜湖人，博士研究生，主要从事测试性试验验证与评估方向的研究。

1671-4598(2016)06-0286-03

10.16526/j.cnki.11-4762/tp.2016.06.078

TP806+.1

A