平板穿透裂纹尖端动态应力强度因子研究*

姜 伟 杨 平1, 董 琴

(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)



平板穿透裂纹尖端动态应力强度因子研究*

姜 伟2)杨 平1,2)董 琴2)

(高性能船舶技术教育部重点实验室1)武汉 430063) (武汉理工大学交通学院2)武汉 430063)

针对含裂纹平板承受冲击载荷时裂纹尖端动态应力强度因子的求解问题，采用将动态有限元分析过程和相互作用积分计算应力强度因子相结合的方法，在有限元分析软件ANSYS中利用APDL编程求解动态应力强度因子.经验证，此方法具有很高的准确性.基于该方法对裂纹长度、裂纹角度、冲击载荷大小对动态应力强度因子的影响进行研究.结果表明，动态Ⅰ型应力强度因子最大值约为相同大小静态载荷应力强度因子的2.6倍；当斜裂纹角度为45°时动态Ⅱ型应力强度因子达到最大值.

动态应力强度因子；相互作用积分；穿透裂纹；冲击载荷

0 引 言

船舶与海洋工程含裂纹结构物在运营期间难免要承受砰击、碰撞等冲击载荷的作用，相较于静态载荷，裂纹在冲击载荷作用下的动态响应不仅需要考虑惯性效应，而且需要考虑应力波在结构内的传播，因此动态断裂问题要比静态断裂问题更加复杂[1].动态断裂问题可以归纳为两类:稳态裂纹在冲击载荷作用下的起裂问题；裂纹在冲击载荷作用下的快速扩展及止裂问题.准确获取裂纹承受冲击载荷时裂纹尖端的动态应力强度因子(DSIFs)，对于研究裂纹在冲击载荷下的起裂和扩展均具有重要意义.

20世纪70年代，Chen等[2]采用有限差分法求解了具有中心穿透裂纹矩形板受冲击载荷作用时裂纹尖端动态应力强度因子，之后该问题成为研究动态应力强度因子的标准问题；90年代，Lin等[3]运用相同方法对Chen问题重新计算，指出应力波传播会导致裂纹尖端动态应力强度因子出现第一次峰值和第二次峰值，Lin的计算结果更加真实准确地描述了动态应力强度因子的变化规律.Stern等[4]提出的相互作用积分可从混合型裂纹J积分中分离出Ⅰ型和Ⅱ型应力强度因子；Song等[5-8]采用相互作用积分计算了均匀和非均匀材料在冲击载荷下的动态应力强度因子.李玉龙等[9-11]分别使用有限元法、裂纹张开位移法和弹簧质量模型方法求解了三点弯曲试样的动态应力强度因子.解德等[12]的论著中，结合虚拟裂纹闭合法和动态有限元分析过程计算了动态载荷下裂纹尖端的动态应力强度因子.Saribay等[13]采用扩展有限单元法计算了冲击载荷下的动态应力强度因子.在高版本有限元软件ANSYS中，已将利用相互作用积分法计算应力强度因子集成到CINT命令中，这无疑为应力强度因子的求解提供了便利.

在有限元分析软件ANSYS中结合动态有限元分析过程和CINT命令，通过APDL编程对含穿透裂纹平板受轴向拉伸冲击载荷作用时的动态响应过程进行了数值仿真，获得了裂纹尖端的动态应力强度因子.经验证，此方法具有很高的准确性.然后基于该方法，分析了裂纹长度、裂纹角度和冲击载荷大小对动态应力强度因子的影响.

1 动态应力强度因子计算原理

1.1 动态有限元方法原理

单元的运动方程可用如下矩阵方程表示.

(1)

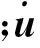
可采用Newmark逐步积分法求解上述运动方程，在时刻t+Δt，单元运动方程如下.

(2)

式中：α,β为控制算法精度和稳定性的2个自由参数.

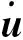
时间步长Δt的选取除了应综合考虑计算时间与计算精度的要求，还应满足如下公式[14]

(4)

(5)

式中：Δl为单元最小尺寸；Cd为纵波波速；E,υ,ρ分别为材料的弹性模量、泊松比和密度.

1.2 相互作用积分法计算应力强度因子的原理

1.2.1 相互作用积分的定义

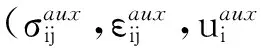
J积分的定义式为[15]

(6)

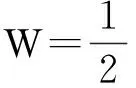
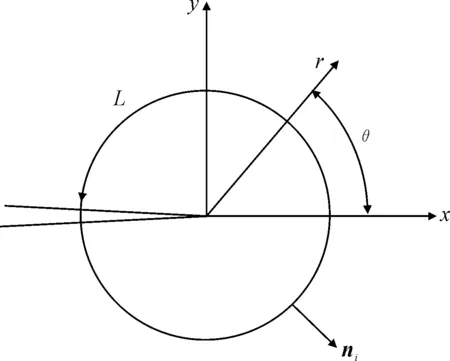
图1 J积分积分路径及法向单位向量

辅助场单独作用引起的J积分为

(7)

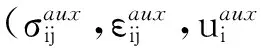
(8)

式中:I即为真实场和辅助场的相互作用积分，其表达式为

(9)

线弹性断裂力学中，应力强度因子K和J积分存在如下关系.

(10)

(11)

式中：KⅠ和KⅡ分别为裂纹尖端的Ⅰ型和Ⅱ型应力强度因子.

由辅助场单独引起的裂纹尖端J积分与应力强度因子K的关系式为

(12)

真实场与辅助场共同引起的J积分与应力强度因子之间的关系式为

(13)

即可得到真实场和辅助场的相互作用积分与应力强度因子之间的关系式为

2.健身休闲企业。健身休闲企业所能提供的大多是场馆类、运动器材或者户外运动类的休闲，此外还应重视各类企业项目供给的创新性与独特性培育。广西要大力支持健身休闲企业发展、鼓励创业创新，应重视龙头企业的培育，充分发挥自主品牌建设和创新能力提升的先导作用。2016年，广西体育馆利用自有事业经营所得收入全额出资成立了广西南国体育投资集团有限责任公司，下设体育赛事、体育建设投资、体育产业发展3个子公司。今后自治区应加大招商引资、项目推介，吸引国内外知名体育组织或大型健身休闲企业落户广西，投资健身休闲产业，建设一批健身休闲特色产业集聚示范区（基地）。

(14)

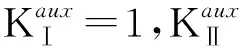
(15)

式中：I(1)和I(2)分别为第一次和第二次求得的相互作用积分.

在高版本的有限元分析软件ANSYS中，只能使用CINT命令实现用相互作用积分法计算应力强度因子.

1.3 求解动态应力强度因子

对承受冲击载荷的穿透裂纹平板做动态有限元分析时，采用APDL编程提取每一时间步长运用CINT命令计算所得的应力强度因子值.绘成曲线即可得到冲击载荷作用下裂纹尖端动态响应的动态应力强度因子曲线.

2 验证算例

采用Chen问题作为验证算例.中心穿透裂纹矩形板受轴向拉伸阶跃冲击载荷，矩形板的宽度2W=20mm、长度2H=40mm，中心穿透裂纹的长度2a=4.8mm，见图2.假设矩形板的材料均匀、各项同性、线弹性，其弹性模量E=199.992GPa，泊松比υ=0.3，材料密度ρ=5 000kg/m3.在矩形板的宽度边上作用阶跃冲击载荷p(t)，大小取p(0)=10MPa，载荷作用时间t=14μs.矩形板选用PLANE183单元，平面应变模型，裂纹尖端采用1/4节点奇异单元.中心穿透裂纹板整体网格划分图，共有3 930个8节点单元，48个6节点奇异单元，12 028个节点.在采用动态有限元分析时，分别取时间间隔Δt为0.05，0.10，0.25μs.

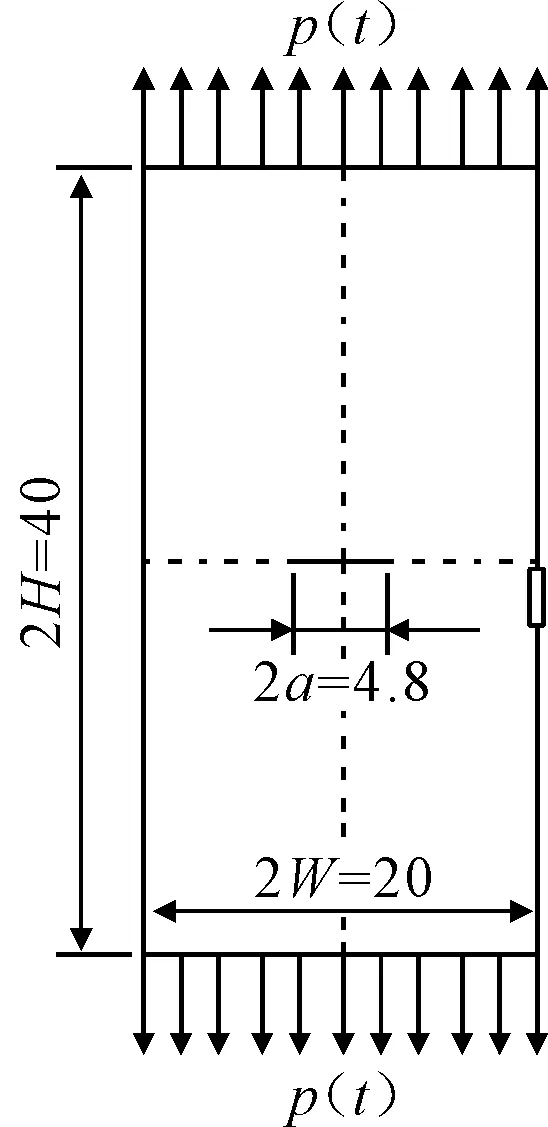
图2 中心穿透裂纹板几何模型及载荷

为便于比较冲击载荷下裂纹的动态响应，采用无限均匀拉伸中心裂纹板的应力强度因子对动态应力强度因子进行量纲一的量处理，量纲一的量动态应力强度因子为

(16)

由式(5)得纵波波速Cd=7 337.85m/s，将载荷作用时间量纲一的量化.

(17)

图3为计算所得量纲一的量动态应力强度因子与Lin的计算结果的对比.结果显示，当Δt=0.05μs时，ANSYS计算结果与Lin的计算结果最为吻合.此方法计算的动态应力强度因子不仅具备很高的准确性，而且能够很准确地反映出裂纹尖端在应力波作用下的动态响应.对于Δt=0.05μs时的计算结果，载荷作用时间t=4.2μs时，动态应力强度因子出现第一次峰值，载荷作用时间t=6.9μs时，动态应力强度因子出现第二次峰值.第二次峰值约为静载荷下裂尖应力强度因子的2.6倍.

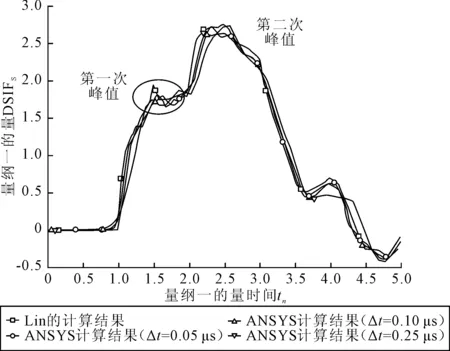
图3 ANSYS计算结果与Lin的计算结果对比

考虑到主要研究拉伸冲击载荷下裂纹的动态响应，未在裂纹面间定义接触，导致2裂纹面发生贯穿，出现负的Ⅰ型应力强度因子.对于裂纹面间的接触摩擦对动态应力强度因子的影响可参考文献[16-17].图4为加载不同时刻矩形板的von-Mises应力云图.

图4 载荷不同时刻中心穿透裂纹板von-Mises应力云图

3 各参数对DSIFs的影响研究

采用相同方法计算Chen问题中不同的裂纹长度、不同裂纹角度和不同冲击载荷大小下的裂纹尖端动态应力强度因子.每次只研究单一因素对动态应力强度因子的影响，其他参数与Chen问题保持一致.冲击载荷作用时间和动态应力强度因子采用与验证算例相同的量纲一的量处理方法.

3.1 裂纹长度对DSIFs的影响

分别取裂纹长度2a为2.0，3.0，4.0mm，计算在各裂纹长度下裂纹尖端动态应力强度因子.计算所得量纲一的量动态应力强度因子曲线见图5，提取动态应力强度因子曲线中第一、二次峰值和时刻(见表1)，t1和t2分别为动态应力强度因子第一次峰值和第二次峰值的时刻.

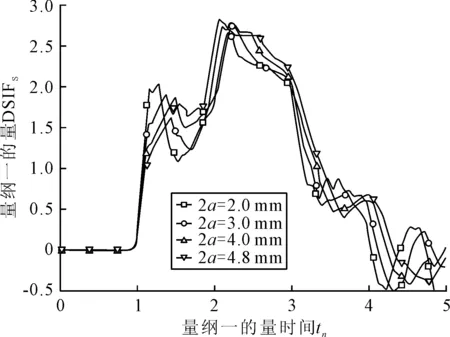
图5 量纲一的量DSIFs曲线(不同裂纹长度)

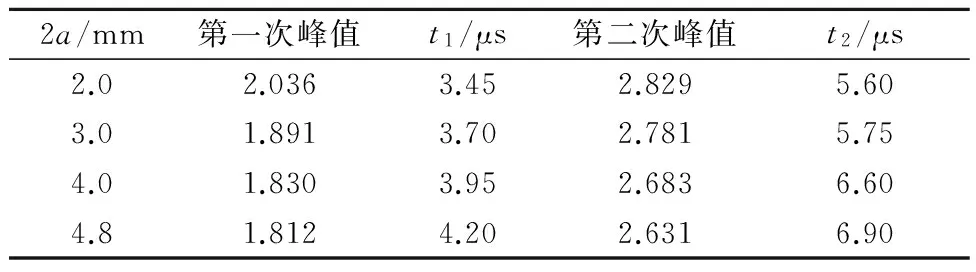
2a/mm第一次峰值t1/μs第二次峰值t2/μs2.02.0363.452.8295.603.01.8913.702.7815.754.01.8303.952.6836.604.81.8124.202.6316.90

由图5可知，裂纹长度越短，裂纹尖端动态响应越剧烈；随着裂纹长度逐渐增加，裂纹尖端动态应力强度因子的第一次峰值和第二次峰值均逐渐减小且峰值发生时刻逐渐延后.从裂纹张开吸收能量的角度考虑，裂纹越短，其所能吸收的能量越小，当受相同大小的冲击载荷时，裂纹的响应越剧烈.

3.2 裂纹角度对DSIFs的影响

实际工程结构中，裂纹绝大部分为复合型裂纹，研究裂纹角度对动态应力强度因子的影响显得尤为必要.斜裂纹的夹角定义为θ，见图6.由于存在裂纹角度，矩形板在承受拉伸载荷时，纯Ⅰ型(张开型)裂纹变为Ⅰ型(张开型)和Ⅱ型(滑开型)复合型裂纹.采用相互作用积分法计算应力强度因子可方便的分离出Ⅰ型和Ⅱ型应力强度因子.

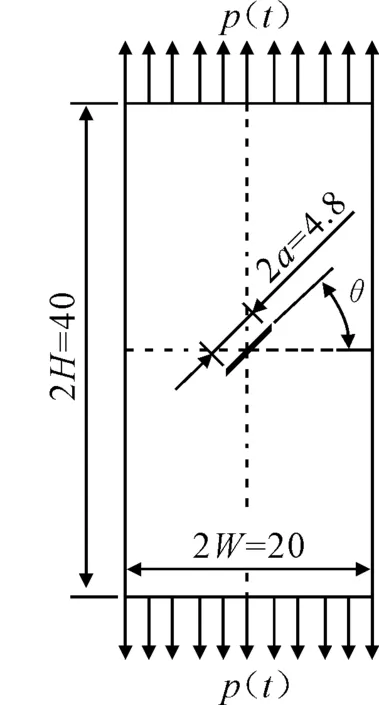
图6 中心穿透斜裂纹板几何模型及边界条件

取裂纹角度θ为15°，30°，45°，60°，75°时计算裂纹尖端动态应力强度因子.图7～8分别为计算所得Ⅰ型、Ⅱ型动态应力强度因子曲线，提取第一、二次峰值和时刻的结果见表2～3.

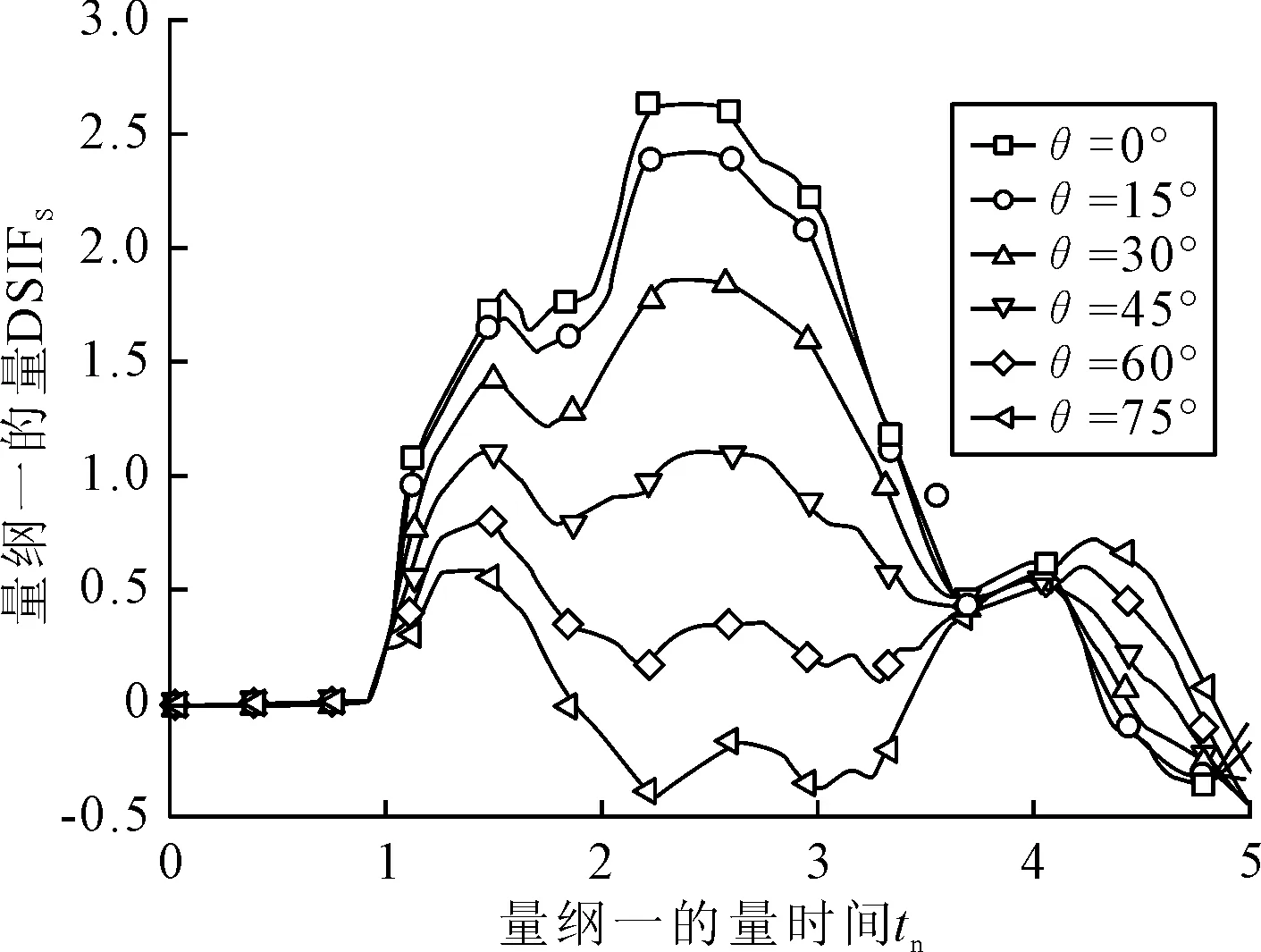
图7 量纲一的量Ⅰ型DSIFs曲线(不同裂纹角度)

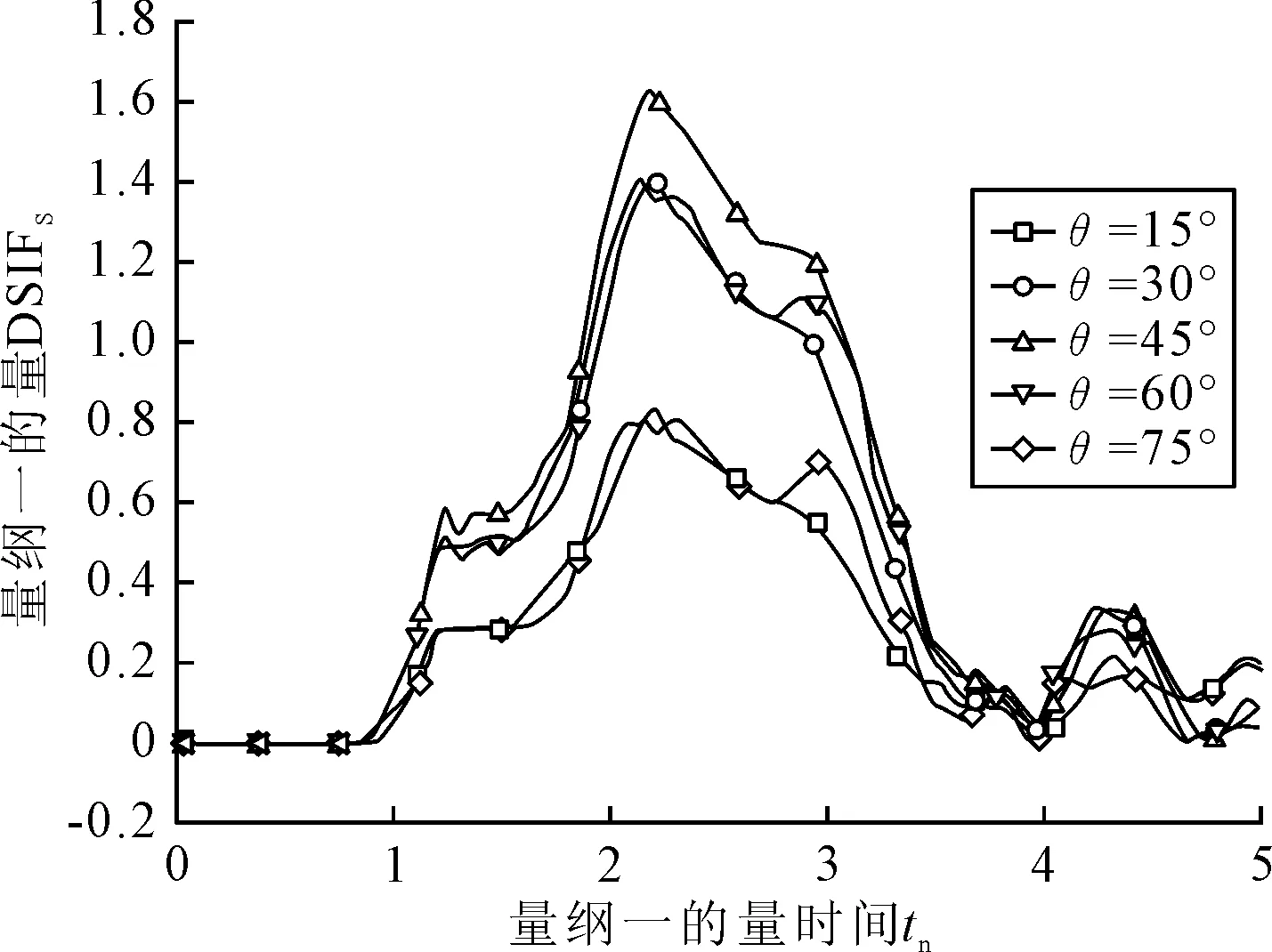
图8 量纲一的量Ⅱ型DSIFs曲线(不同裂纹角度)

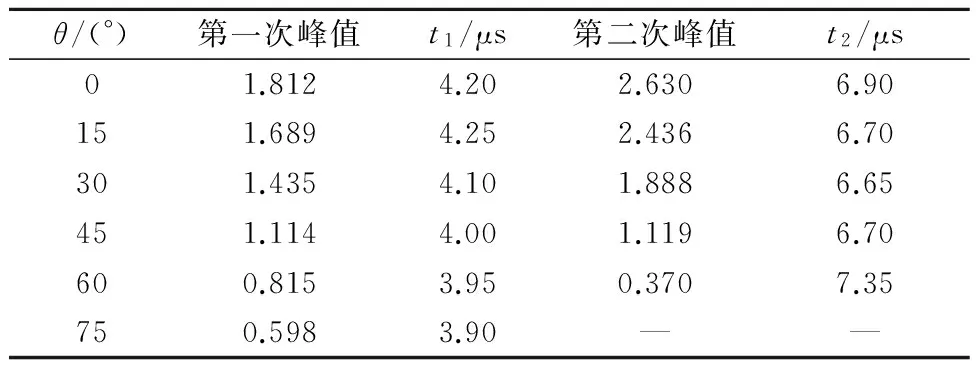
θ/(°)第一次峰值t1/μs第二次峰值t2/μs01.8124.202.6306.90151.6894.252.4366.70301.4354.101.8886.65451.1144.001.1196.70600.8153.950.3707.35750.5983.90——

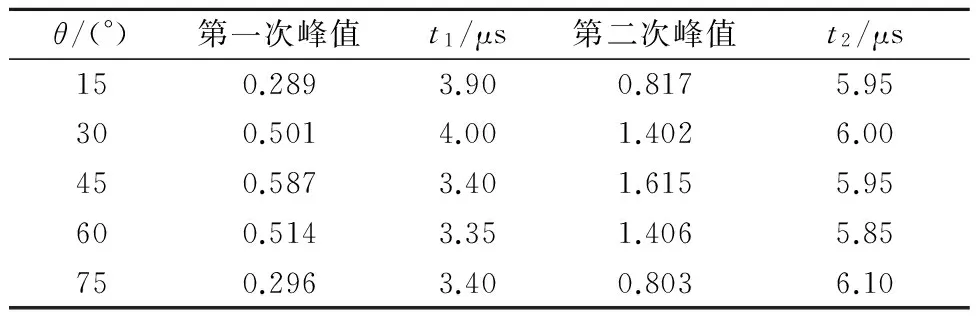
表3 Ⅱ型DSIFs峰值和时刻(不同裂纹角度)

结果表明，随裂纹角度增加，Ⅰ型动态应力强度因子逐渐减小，由于裂纹尖端距宽度边的距离变短，第一次峰值和第二次峰值发生时刻逐渐提前.当裂纹角度θ=45°时，裂纹尖端Ⅱ型动态应力强度因子达到最大值；θ=30°和θ=60°的Ⅱ型动态应力强度因子相差不大；θ=15°和θ=75°的Ⅱ型动态应力强度因子也相差不大，但均小于裂纹角度θ=30°和θ=60°时的Ⅱ型动态应力强度因子，Ⅱ型动态应力强度因子峰值时刻基本相同.

3.3 载荷大小对DSIFs的影响

取冲击载荷p(t)为6,8,12，14 MPa，冲击载荷作用时间仍为14 μs，计算在各冲击载荷下裂尖动态应力强度因子.

图9为计算所得量纲一的量动态应力强度因子曲线.若采用与冲击载荷大小相同的静载荷应力强度因子作量纲一的量处理，得出的动态应力强度因子曲线见图10.峰值和时刻提取结果见表4.

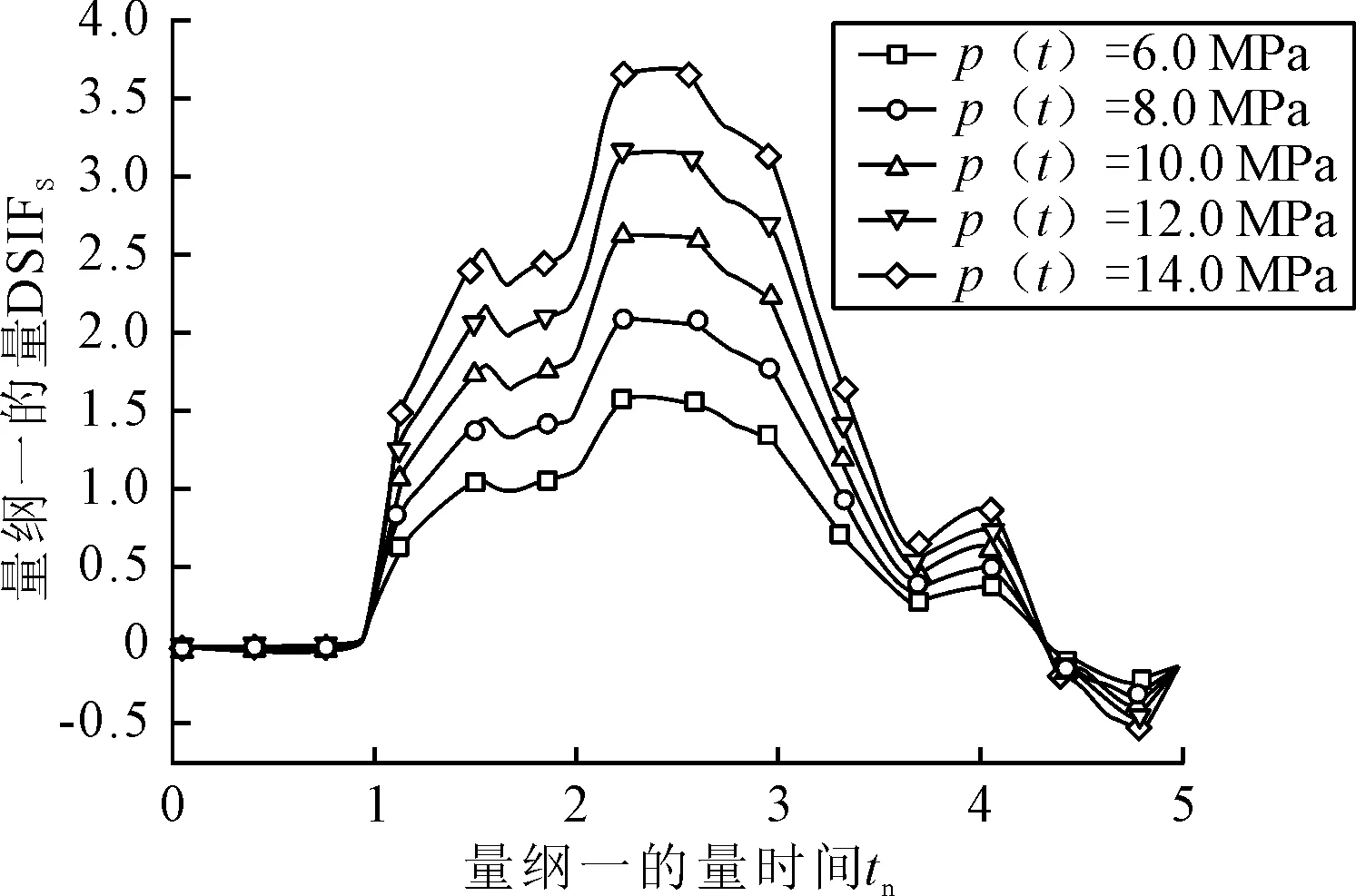
图9 量纲一的量DSIFs曲线(不同载荷大小)

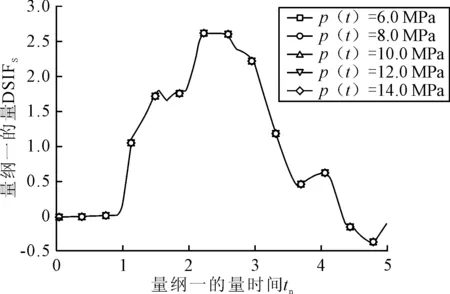
图10 量纲一的量DSIFs曲线(不同载荷大小)

结果表明,动态应力强度应子大小与载荷大小呈线性递增关系，冲击载荷大小不影响裂纹动态响应的时间.动态应力强度因子最大值约为相应静态载荷应力强度因子的2.6倍.

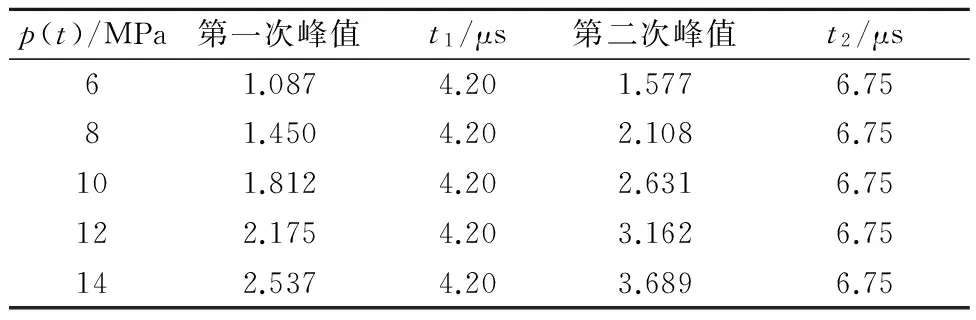
表4 DSIFs峰值和时刻(不同载荷大小)

4 结 论

1) 在有限元软件ANSYS中，将利用相互作用积分法计算静裂纹断裂参数的CINT命令和动态有限元分析过程相结合，可准确地计算冲击载荷下的静裂纹问题.

2) 对于中心穿透垂直裂纹平板，裂纹越短，裂纹在冲击载荷下的动态响应越剧烈；随着裂纹长度的增加，动态应力强度因子的第一次峰值和第二次峰值均逐渐减小，峰值出现时间逐渐延后.对于中心穿透斜裂纹平板，随着裂纹角度的增加，动态Ⅰ型应力强度因子逐渐减小；当裂纹角度θ=45°时，动态Ⅱ型应力强度因子达到最大值.

3) 冲击载荷越大，动态应力强度因子越大.对于Chen问题中的材料参数，动态应力强度因子最大值约为相同大小静态载荷应力强度因子的2.6倍.

[1]范天佑.断裂动力学引论[M].北京：北京理工大学出版社，1990.

[2]CHEN Y M. Numerical computation of dynamic stress intensity factors by a Lagrangian finite-difference method (the HEMP code)[J]. Engineering Fracture Mechanics,1975(7):653-660.

[3]LIN X, BALLMANN J. Re-consideration of Chen’s problem by finite difference method[J]. Engineering Fracture Mechanics,1993(5):735-739.

[4]STERN M, BECHER E B, DUNHAM R S. A contour integral computation of mixed-mode stress intensity factors[J]. International Journal of Fracture,1976,12(3):359-368.

[5]SONG S H, PAULINO G H. Dynamic stress intensity factors for homogeneous and smoothly heterogeneous materials using the interaction integral method[J]. International Journal of Solids and Structures,2006,43(16):4830-4866.

[6]YU H J, SUMIGAWA W, WU L Z, et al. Generalized domain-independent interaction integral for solving the stress intensity factors of nonhomogeneous materials[J]. International Journal of Solids and Structures,2015(67):151-168.

[7]于洪军.含复杂界面非均匀材料断裂力学研究[D].哈尔滨：哈尔滨工业大学，2010.

[8]WANG Z Y, MA L, YU H J, et al. Dynamic stress intensity factors for homogeneous and non-homogeneous materials using the interaction integral method[J]. Engineering Fracture Mechanics,2014(128):8-21.

[9]李玉龙，刘元镛.带裂纹板在冲击载荷作用下动态应力强度因子的数值计算[J].航空学报，1989，10(5)：227-233.

[10]李玉龙，刘元镛.用裂纹张开位移计算三点弯曲试样的动态应力强度因子[J].爆炸与冲击，1993，13(3)：249-256.

[11]李玉龙，刘元镛.用弹簧质量模型求解三点弯曲试样的动态应力强度因子[J].固体力学学报，1994，15(1)：75-79.

[12]解德，钱勤，李长安.断裂力学中的数值计算方法及工程运用[M].北京：科学出版社，2009.

[13]SARIBAY M, NIED H F. Dynamic stress intensity factors for suddenly loaded structures using enriched finite elements[J]. Theoretical and Applied Fracture Mechanics,2014(70):59-67.

[14]MURTI V, VALLIAPAN S. The use of quarter point element in dynamic crack analysis[J]. Engineering Fracture Mechanics,1986(23):585-614.

[15]RICE J R. A path-independent integral and the approximate analysis of strain concentration by notches and cracks[J]. Journal of Applied Mechanics,1968,35(2):379-386.

[16]王立清，盖秉政.有限板中圆孔边单边斜裂纹动态应力强度因子的数值计算[J].工程力学，2009，26(3)：9-14.

[17]王立清，盖秉政.裂纹面接触摩擦对双-边裂纹板动态应力强度因子的影响[J].工程力学，2009，26(7)：7-11.

Research on Dynamic Stress Intensity Factors for Through-cracked Plates

JIANG Wei2)YANG Ping1,2)DONG Qin2)

(KeyLaboratoryofHighPerformanceShipTechnologyofMinistryofEducation,Wuhan430063,China)1)(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)2)

In order to obtain the dynamic stress intensity factors (DSIFs) of a cracked plate subjected to impact load, the method by combining the dynamic finite element analysis process and the interaction integral method is used. APDL can be used to evaluate the DSIFs in the finite element software ANSYS. This method is verified and has a high accuracy. Besides, the influences of crack length, crack angel and impact load magnitude to the DSIFs are investigated and discussed. The results show that the maximum of the I type DSIFs is about 2.6 times the magnitude of SIF with the same size static load. When the inclined crack with 45 degrees, the II type DSIFs reaches the maximum.

dynamic stress intensity factors (DSIFs); interaction integral; through crack; impact load

2016-08-10

*国家自然科学基金项目资助(51479153)

U661.42 doi:10.3963/j.issn.2095-3844.2016.05.012

姜伟(1987- )：男，博士生，主要研究领域为结构疲劳与断裂