碰撞凹陷损伤下加筋板结构的崩溃分析*

施兴华 包 均 钱 鹏 卞璇屹

(江苏科技大学船舶与海洋工程学院 镇江 212003)



碰撞凹陷损伤下加筋板结构的崩溃分析*

施兴华 包 均 钱 鹏 卞璇屹

(江苏科技大学船舶与海洋工程学院 镇江 212003)

采用球撞击加筋板形成凹陷，选取3种典型的凹陷位置，即板格中间、翼板中间和板格所在加筋处中间.保持撞击后的变形状态，在加筋板的两侧施加逐步增加的轴向压力，以获得其崩溃状态，最终得到凹陷损伤加筋板的极限强度.分析5种不同的速度和不同的重量对加筋板极限强度的影响，并讨论了凹陷损伤下加筋板的失效模式及凹陷深度对加筋板极限强度的影响.计算结果表明，凹陷的存在削弱加筋板的极限强度，而且随着凹陷面积和凹陷深度的增加，极限强度减小更加明显；凹陷在板格中间对加筋板的承载能力影响最大；不同撞击部位的凹陷损伤加筋板结构在轴向压缩载荷下会出现不同的失效模式.

加筋板；凹陷；极限强度；撞击

0 引 言

船舶在其生命周期内会发生各种损伤，外物损伤(foreign object damage)是其中的一种形式，它可能由于货物不当的装载卸载而产生.船体加筋板被外物撞击会产生凹陷，凹陷会影响船舶的强度，对船舶的安全运行产生隐患.

Dow等[1]对局部缺陷矩形板的屈曲和后屈曲行为进行了研究，结果表明，局部缺陷的幅值对矩形板极限强度影响较大，局部缺陷的形状和位置对其影响较小.Paik等[2-3]模拟钢板在受轴压和剪切载荷条件下，凹陷的大小、板的厚度及纵横比对极限强度的影响.结果表明，板的厚度和纵横比对板的崩溃模式影响很大.Luis等[4]分析了轴压下局部缺陷对钢板崩溃模式的影响.An等[5]提出了受凹陷影响的船体结构基于极限强度折减系数的可靠性计算公式.Raviprakash等[6-8]研究方形钢板在单轴压缩条件下凹陷方向对极限强度的影响，其结果显示，横向凹陷比纵向凹陷对极限强度的影响更大.上述研究揭示了凹陷板极限强度的一些特性，但较少考虑凹陷尺寸(深度和面积)对加筋板极限强度的影响.

文中首先通过模拟物体掉落对于船体加筋板的非线性碰撞分析，获得相应的凹陷缺陷，在此基础上，进行凹陷损伤加筋板的极限强度研究，获得其凹陷缺陷下的崩溃机理分析重物掉落速度，重量及撞击位置的不同对于具有凹陷加筋板结构极限承载力的变化趋势.文中结论对分析含凹陷的船舶与海洋工程结构极限强度、确定凹陷构件维修或更换具有重要的工程指导意义.

1 计算模型

结构的碰撞损伤及其极限强度问题都将涉及到材料的非线性，以及几何非线性，分析过程中需要计入结构材料的弹塑性本构关系，并需要考虑大应变的影响.非线性数值模拟技术在碰撞问题中已经得到很好的利用，Ansys/Ls-dyna的显示分析技术已经能够较为准确地预报结构碰撞引起的凹陷损伤[9].在极限强度分析方面，目前的结构非线性有限元已经成为结构极限强度分析的重要手段，当建模技术足够准确时，能给出精确的分析结果.有限元法另一个重要的优点在于可以方便地分析任意形式结构的极限强度，并可考虑初始缺陷及任意复杂加载的影响，这是文中选取该方法进行结构极限强度分析的重要原因[10-11].

为了在合理使用计算机资源的基础上得到较为精确的分析结果，需要考虑碰撞及加筋板极限承载力分析的合理的模型范围，因其与计算模型边界条件的设置和分析时间是息息相关的.当双跨模型的屈曲模态为奇数波形时，其边界条件与单跨模型一致，双跨模型(1/2+1+1/2)相比于单跨模型，能得到更加贴近于真实情况的转动自由度约束.因此文中选取的加筋板模型见图1.表1给出了加筋板的几何尺寸.加筋板屈服强度σy为315 MPa，弹性模量E为2.1×105MPa，泊松比为0.3.考虑到重物跌落碰撞损伤属于低速碰撞问题，结构的极限强度为准静态力学过程，因此，采用理想弹塑性模型来进行结构的碰撞，以及极限强度的分析.

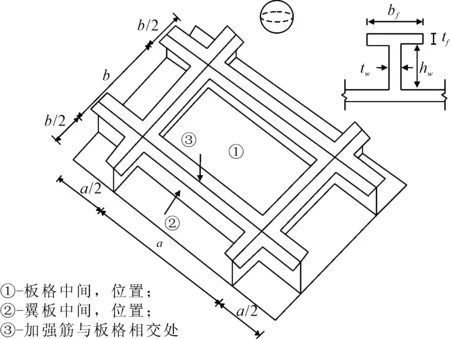
图1 撞击模型示意图

mm

abhwbftptwtf8600163048017217.8817

2 凹陷区域的模拟

文献[3]表明，在凹陷的幅值一定的情况下，凹陷形状对板格极限强度的影响很小.因此，文中通过加筋板上所有凹陷均由球撞击而成.采用显式有限元程序LS-DYNA进行球与加筋板的碰撞过程的模拟，得出结构所有节点的位移改变量，选取加筋板结构的碰撞模型作为含凹陷结构极限强度的分析模型，研究加筋板极限强度的变化趋势.

选取典型的3处加筋板的撞击位置，对于每一种模型，考虑不同高度的重物掉落，选取5种不同的速度8，9，10，11，12 m/s，以及5种不同重量263，514，888，1 410，2 104 kg,3种典型凹陷位置的有限元模型图见图2，分析不同速度和重量所形成的凹陷对加筋板极限强度的影响.

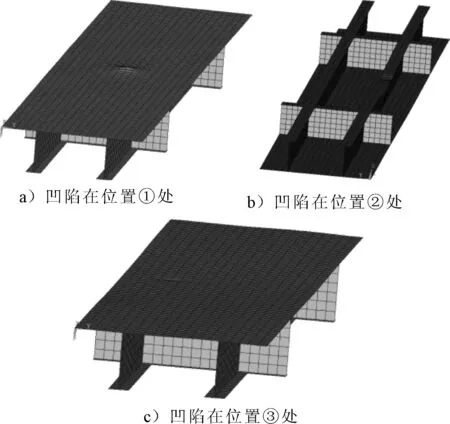
图2 3种典型凹陷位置的有限元模型图

加筋板是船舶结构的重要组成部分，在船舶受撞击过程中，加筋板X轴方向是固定的，不会发生平移现象.选取的边界条件为当X=0时，UX固定(即UX=0).并在X轴方向施加压缩载荷，分析凹陷损伤下加筋板在单轴压缩载荷作用下的崩溃过程.

3 含凹陷损伤加筋板的极限承载力分析

3.1 凹陷在位置①处

在撞击过程中，球以10 m/s的速度撞击加筋板板格中间位置，凹陷深度随着球重量的增大而加深.凹陷形状见图2a).图3为凹陷在板格中间的加筋板变形和应力云图.由图3可知，随着撞击球重量的增大应力分布变化不大，但凹陷的深度逐渐增大，加强筋的屈曲破坏模式发生了变化，2条加强筋由向内侧弯变为了向外侧弯.应力分布沿着加筋板长轴对称分布，加筋板在两横梁之间发生屈曲变形，并在这个范围内出现了应力集中，两条加强筋发生了明显的侧弯，板格中部也发生显著屈曲变形.在单轴压缩载荷作用下，横梁的应力水平较低，对加筋板起到了一定的支撑作用.

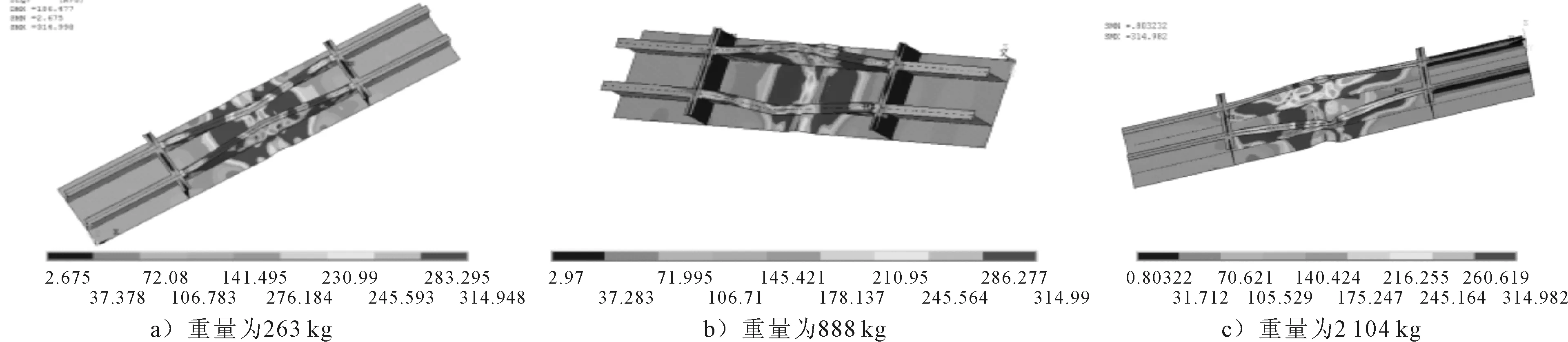
图3 ①处凹陷在板格中间的加筋板变形-应力云图(不同撞击重量)

表2为不同凹陷深度的极限强度，凹陷深度增大的程度指的是相比于263 kg重物撞击所产生的凹陷，其他重量撞击产生的凹陷幅值的增大百分比，凹陷面积指的是板面被撞击后发生变形面的投影面积，极限强度的降低程度是相对于完整加筋板结构的降低百分比.随着球重量的增大，凹陷深度明显增大，最大凹陷深度增大程度达到58.878 mm，这说明，在同等速度的条件下，重量越大，球的冲量越大，撞击的效果越强，形成的凹陷深度也越大，对应加筋板的极限强度值越小.同时可以看出，凹陷面积相同时，凹陷深度的增大使极限强度值减小；当凹陷面积和深度同时增大时，极限强度值显著减小.

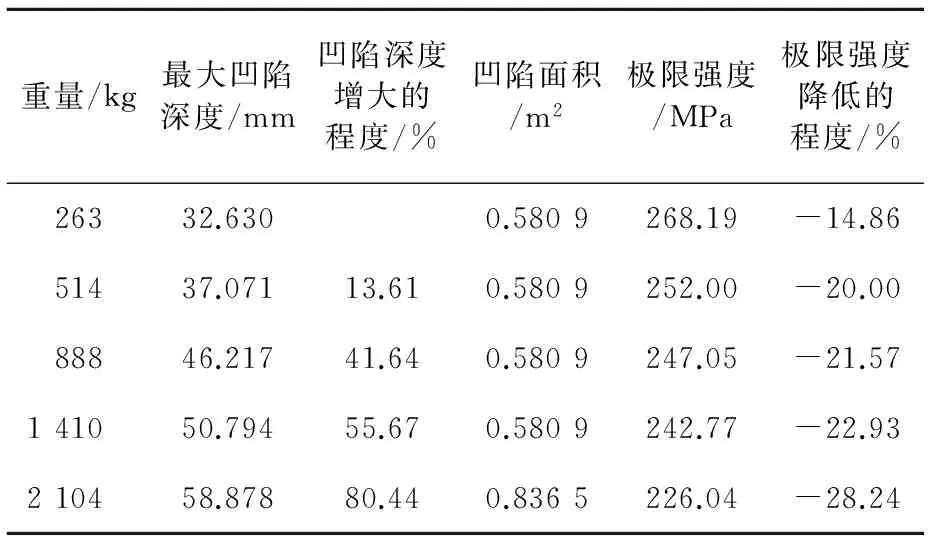
表2 ①处不同凹陷深度的极限强度(不同撞击质量)

同样可以从图4的应力-应变曲线图中看出，撞击重量为263,514，888，1 410 kg的4条应力-应变曲线在结构屈曲前呈线性变化，且斜率几乎保持一致，在凹陷深度增加的情况下，最大应力值减小缓慢.重量为2 104 kg的应力-应变曲线在线性阶段的斜率明显小于其他4条曲线，且凹陷面积最大，最大应力值相对于其他4条曲线下降明显.表明大面积大深度的凹陷损伤将会显著地减小结构的刚度及其极限承载能力.

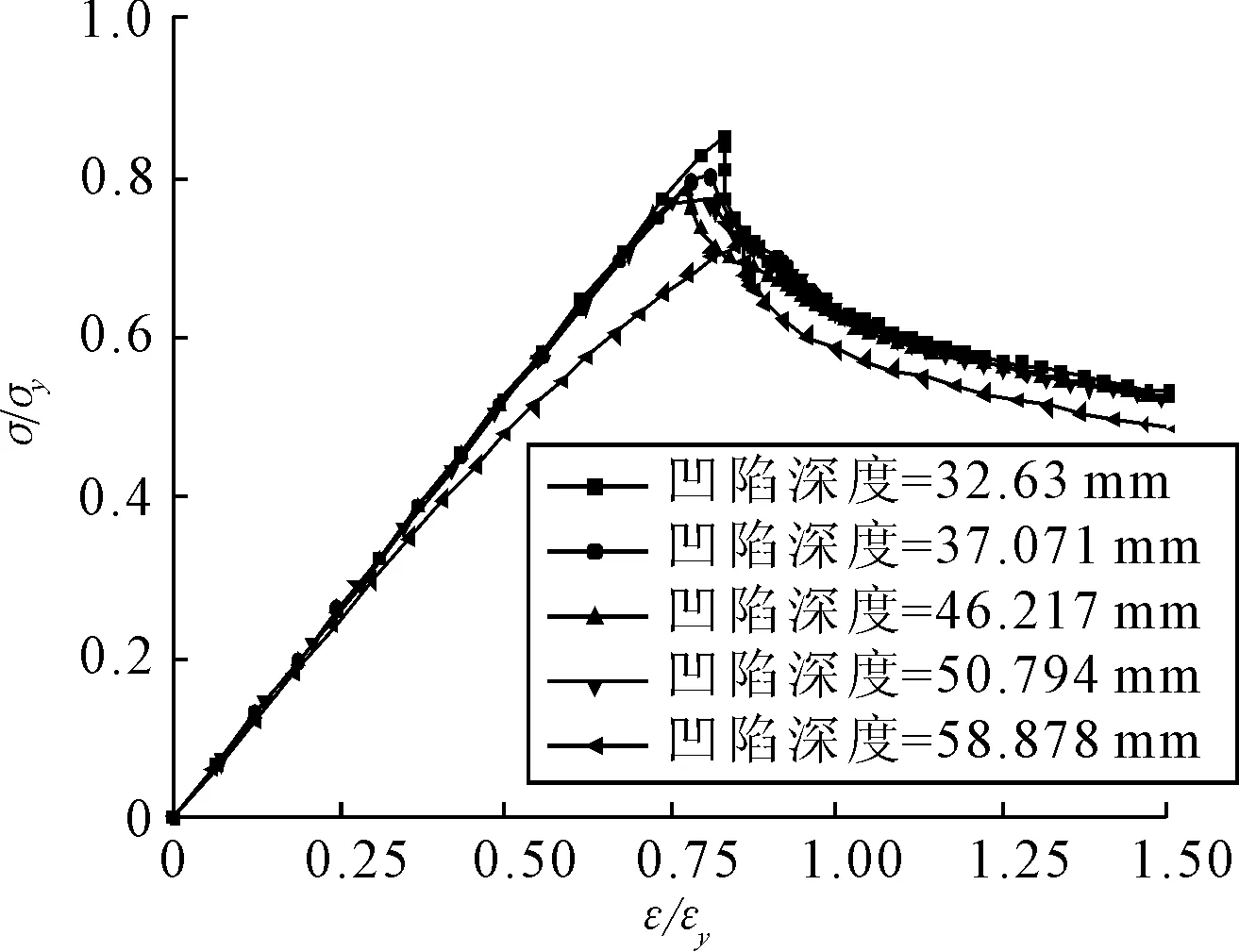
图4 ①处量纲一的量应力-应变曲线图

撞击位置依然在板格中间，保持球的重量不变(取球重量为514 kg)，分析不同碰撞速度引起的凹陷损伤及凹陷加筋板极限强度的变化趋势，见图5.由图5可见，加筋板发生弯曲变形的区域集中在两横梁中部，横梁两侧(包括横梁)几乎没有变化.与图3情况类似，2条加筋在轴向压力的作用下，发生明显的侧弯，凹陷所在的板格中部区域也发生显著的屈曲变形，这与撞击的区域基本吻合.当速度增大到12 m/s时，2加强筋的变形模式发生了明显的改变.

图5 ①处凹陷在板格中间的加筋板变形-应力云图(不同碰撞速度)

表3为不同凹陷深度的极限强度.由表3可知，同一重量的球，随着速度增大，其凹陷深度在加深，对应的极限强度值逐渐减小，但数值减小的趋势不大.这表明，在凹陷面积不变时，凹陷深度越大，加筋板的极限强度下降趋缓.这一规律在图6中也可以得到，4条应力-应变曲线在线性阶段的斜率变化不大，几乎一致，但随着凹陷深度的加深，其最大应力值在减小.

3.2 凹陷在位置②处

在撞击过程中，球以10 m/s的速度撞击加筋板翼板中间位置，其凹陷深度随着球重量的增大而加深.凹陷形状见图2b).被撞击的加强筋在轴向压缩载荷下发生明显的侧弯，见图7.这表明，相比于完整的加强筋，凹陷的存在改变了其失效模式，在轴向压缩载荷的逐步作用下，凹陷损伤加筋发生了侧倾破坏，降低了整体的极限强度.随着重量的增加，凹陷深度随之增加，极限强度值随之减小，其差值也越来越大,见表4.这说明单根加强筋的凹陷对整个加筋板的极限强度有较大的影响，其变化趋势是随着凹陷深度的增加而明显减小.

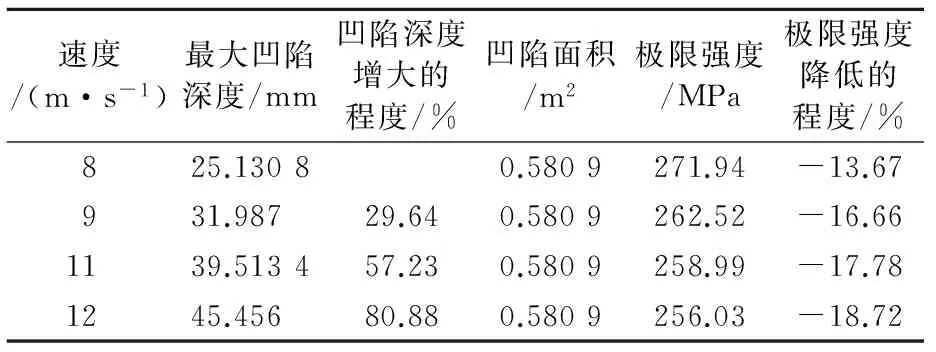
表3 ①处不同凹陷深度的极限强度(不同撞击速度)

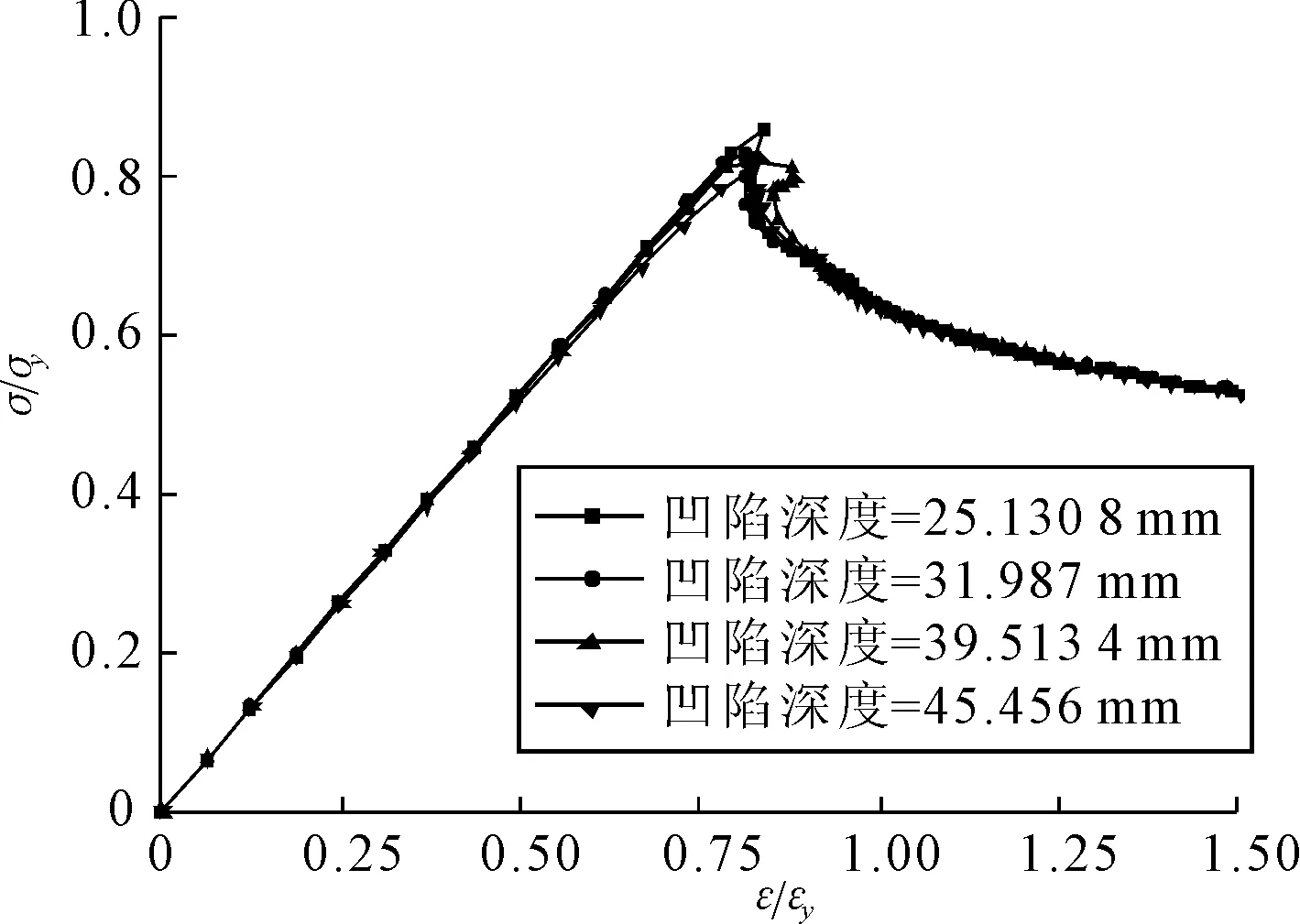
图6 ②处量纲一的量应力-应变曲线图

图7 ②处凹陷在翼板中间的加筋板变形-应力云图(不同撞击重量)

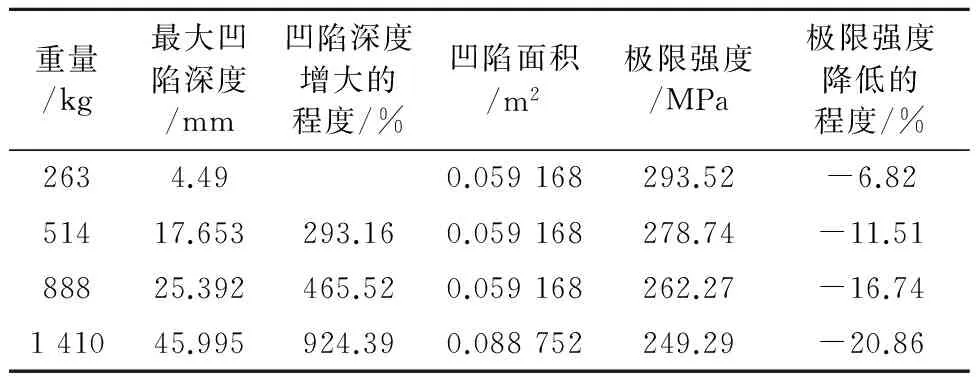
重量/kg最大凹陷深度/mm凹陷深度增大的程度/%凹陷面积/m2极限强度/MPa极限强度降低的程度/%2634.490.059168293.52-6.8251417.653293.160.059168278.74-11.5188825.392465.520.059168262.27-16.74141045.995924.390.088752249.29-20.86

同一重量的球(球重量为514 kg)，随着速度增大，形成的凹陷深度也越来越深，对应的极限强度值越来越小，见表5.被撞击的加筋，在轴向压力的作用下，发生侧倾变形，整块加筋板除了横梁外都进入塑性状态，见图8.在加筋板纵向受压过程中，横向构件对其有一定的支撑作用；凹陷的存在将削弱加筋板的极限强度，而且极限强度是随着凹陷深度的加深而减小.

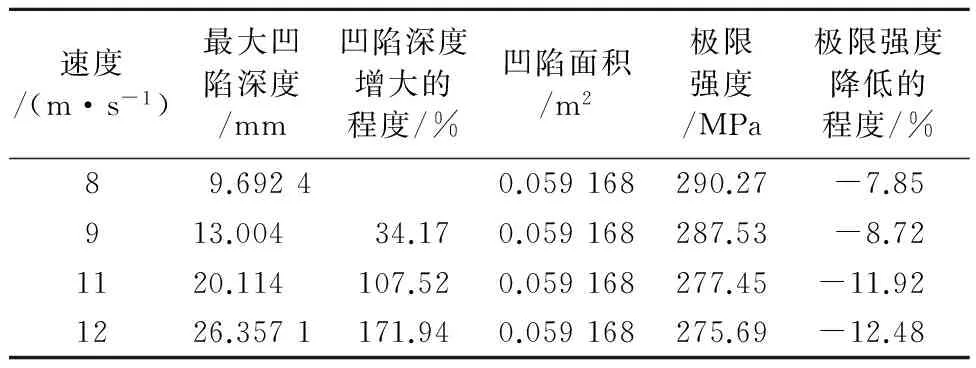
表5 ②处不同凹陷深度的极限强度(不同撞击速度)

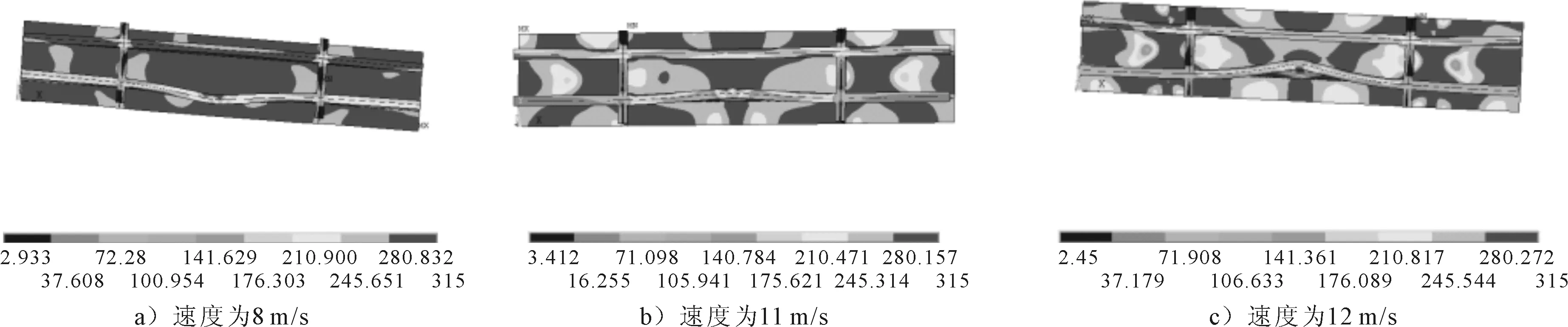
图8 ②处凹陷在翼板中间的加筋板变形-应力云图(不同撞击速度)

3.3 凹陷在位置③处

图9为凹陷在板格与加强筋相交处的变形-应力云图.当碰撞发生于板格与加强筋的连接处时，板格和加强筋同时发生凹陷损伤.

球重量成倍数的增加，凹陷深度由浅入深越来越大，变化趋势也由缓变陡，对应的加筋板极限强度值越来越小，见表6.当凹陷面积一样时，虽然凹陷深度在增加，但极限强度减小缓慢；当凹陷面积和凹陷深度成倍增大时，加筋板的极限强度值急剧减小.重量为263 kg和888 kg的应力-应变曲线在塑性变形前呈线性状态，其斜率吻合，应力-应变的拐点值为0.92和0.90，见图10.

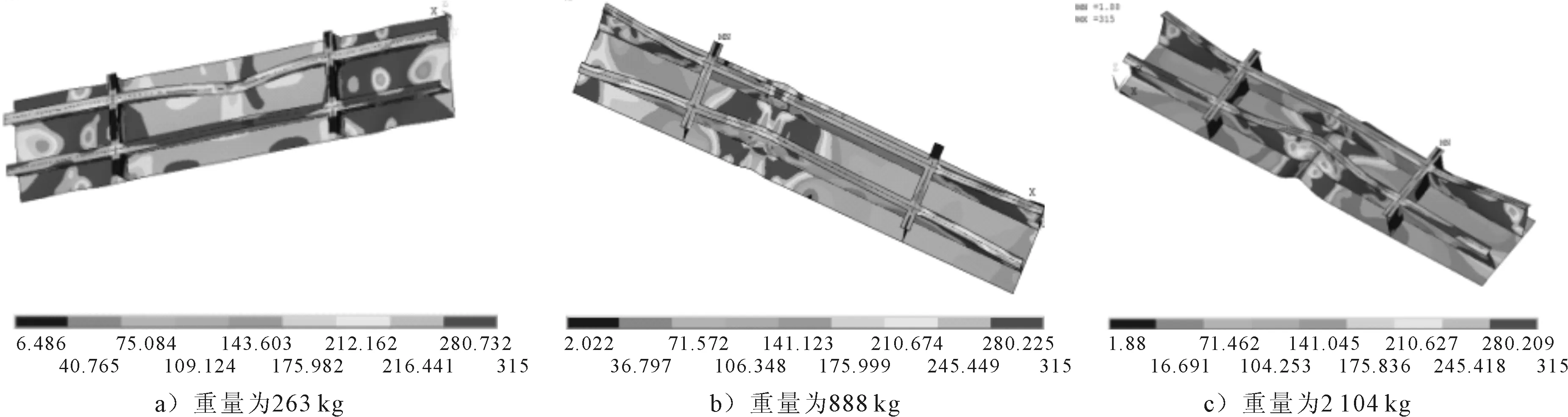
图9 ③处凹陷在板格与加强筋相交处的应力云图(不同撞击重量)

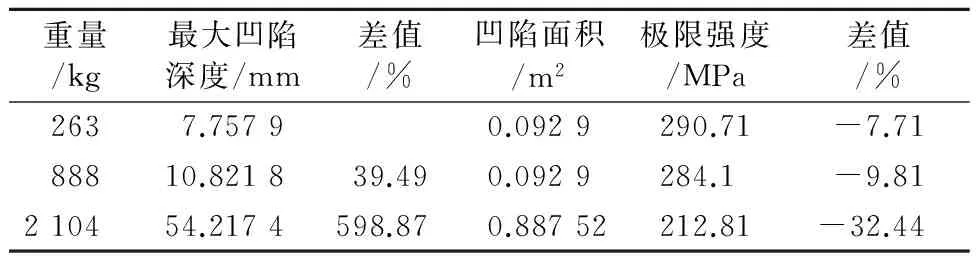
重量/kg最大凹陷深度/mm差值/%凹陷面积/m2极限强度/MPa差值/%2637.75790.0929290.71-7.7188810.821839.490.0929284.1-9.81210454.2174598.870.88752212.81-32.44

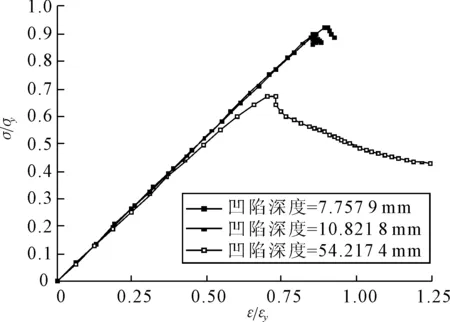
图10 ③处量纲一的量应力-应变曲线图(不同撞击重量)

当刚性球的重量提升到2 104 kg时，其应力-应变曲线在线性阶段斜率减小，加筋板的整体刚度降低，对应的最大应力值也显著减小，为0.67.这表明，凹陷在位置③处将会影响加筋板的极限强度，对比完整加筋板结构，含凹陷加筋板极限强度下降明显，而且随着凹陷深度的增加，极限强度值随之减小.然而在同一凹陷面积状态下，虽然凹陷深度在增加，但极限强度值减小缓慢，变化趋势不明显.只有凹陷面积和深度增大时，极限强度值才会显著减小.

在速度增加的同时，撞击形成的凹陷深度也在增加，但它们的凹陷面积相同，对应的极限强度值虽在减小却减小缓慢，见表7.从应力-应变曲线图11中可知，4种速度情况的应力-应变曲线在塑性变形前呈线性状态的斜率相同，最大应力值也很接近.因此可以验证，其一凹陷对加筋板极

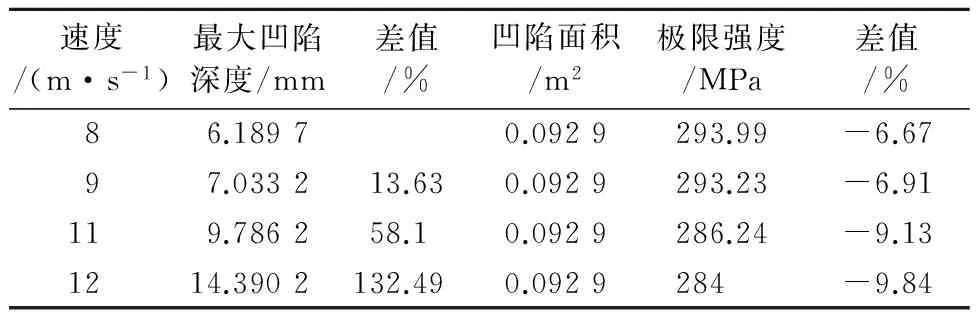
表7 ③处不同凹陷深度的极限强度(不同撞击速度)

限强度有削弱作用；其二相比于凹陷深度，凹陷面积对于结构的极限强度影响较大.

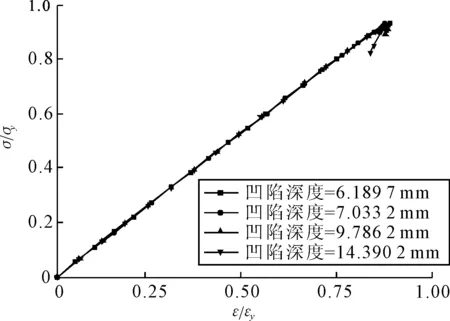
图11 ③处量纲一的量应力-应变曲线图(不同撞击速度)

4 碰撞凹陷下加筋板的崩溃分析

4.1 失效模式分析

碰撞凹陷损伤分别发生在板格(或是板格处与加强筋相连接)以及加筋处，将会引起加筋板结构在轴向压缩载荷下发生不同的失效模式：

1) 板格的屈曲失效而引起整体结构的崩溃 从板格处凹陷损伤的加筋板的极限承载能力曲线(见图4)可看出，板格的凹陷损伤引起板格的局部屈曲失效而导致加筋板极限强度的降低，其降低程度约为20%，见表2.从应力云图(图3)可见，其屈曲失效基本发生在凹陷的截面处，由于该截面处的局部变形导致结构的变形过大而失效.

2) 加强筋的侧倾失效而导致整体结构的崩溃 凹陷损伤发生于加强筋时，加筋板极限强度降低主要原因是加强筋发生了侧倾屈曲.由图7和图8可知，发生凹陷损伤的加强筋侧向变形很大，此时该加强筋发生侧倾失效，该局部屈曲进而引起整个加筋板的失效.

3) 板格、加强筋的联合屈曲而引起的结构失效 当碰撞发生于板格与加强筋的连接处时，板格和加强筋同时发生凹陷损伤，板格的屈曲和加强筋的侧倾屈曲可能同时发生，见图9.

4.2 凹陷深度的影响

对于凹陷损伤的加筋板格，其极限强度的计算具有高度的非线性，很难用解析方法精确求解.由上文的分析结果可知，凹陷深度是影响凹陷加筋板极限强度的主要因素之一.图12～14给出了3种碰撞位置下凹陷深度与相对极限强度的关系曲线，表明凹陷深度的增加与相对极限强度基本呈线性关系.图中，dmax为凹陷深度的最大值；σu/σu0为相对极限强度；σu为凹陷损伤加筋板的极限强度；σu0为无凹陷损伤加筋板的极限强度.

比较这3中情况的凹陷损伤，碰撞发生于板格中心时，凹陷损伤较大；由于加强筋的刚度较大，相同重量、相同深度的碰撞引起的凹陷损伤小于板格，因此，其极限强度的降低程度也小于板格处发生凹陷损伤的情况，碰撞发生于板格与加强筋的连接处的情况，凹陷损伤和极限强度的降低程度介于这两者之间.

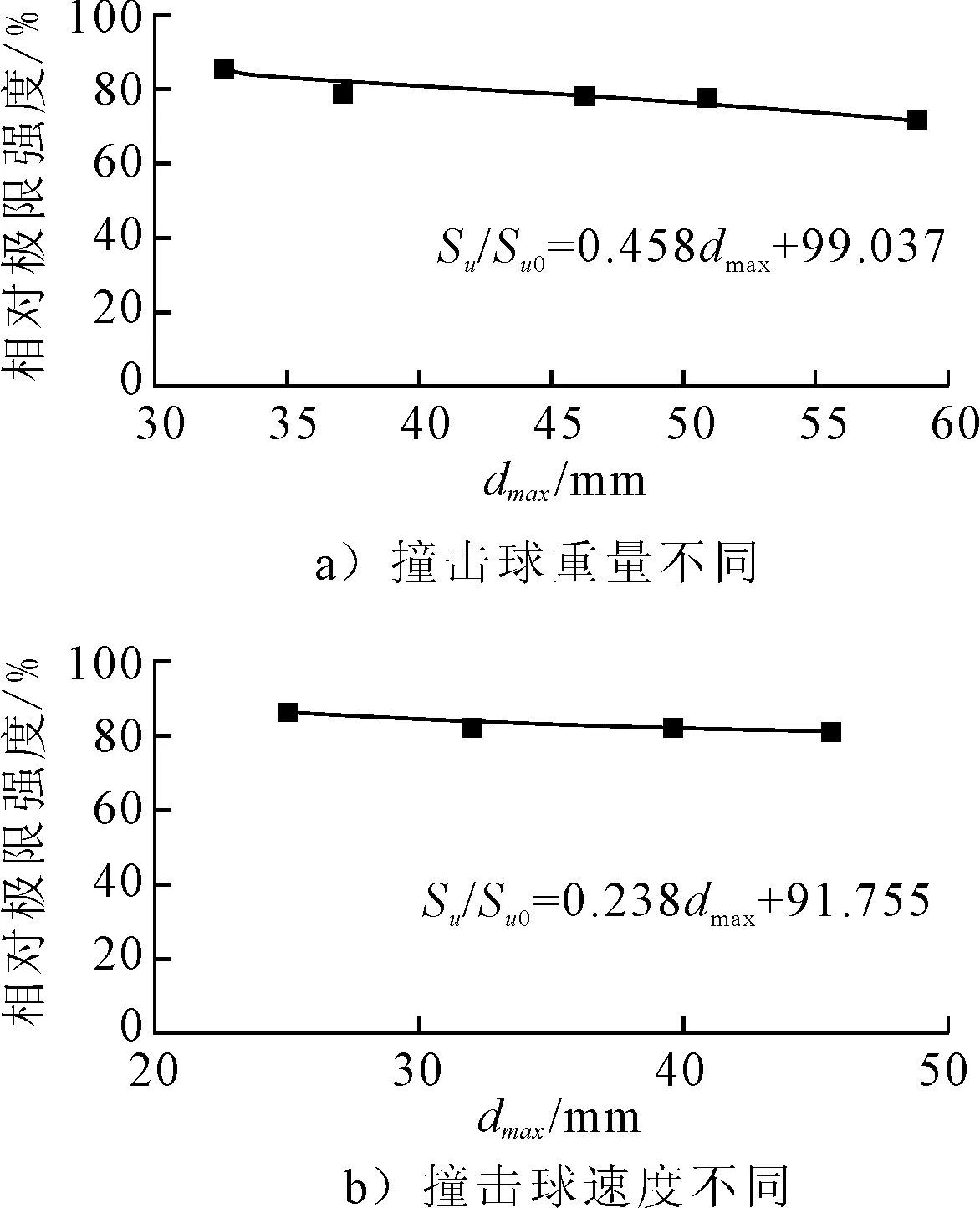
图12 凹陷在加筋板板格中间的相对极限强度

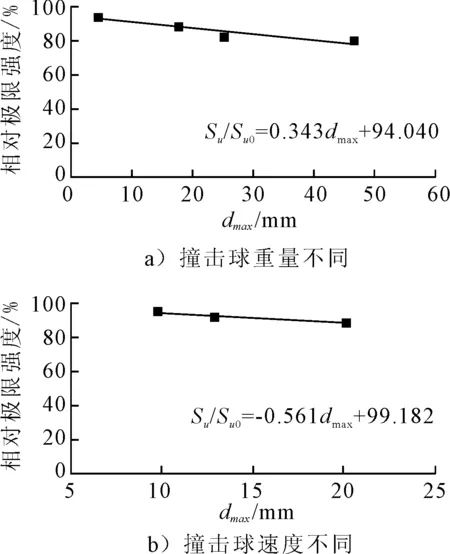
图13 凹陷在加强筋翼板中间的相对极限强度

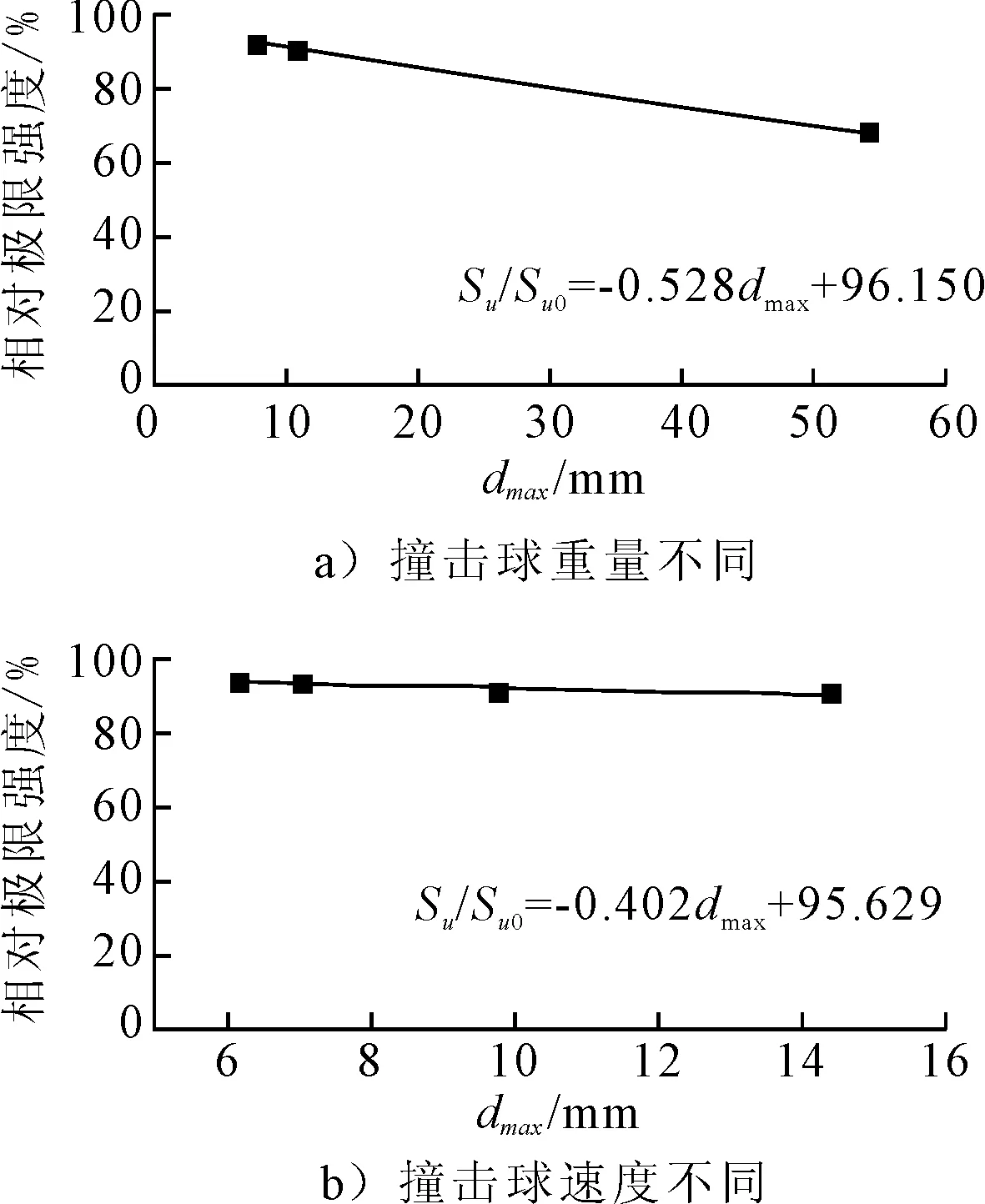
图14 凹陷在板格处于加强筋中间的相对极限强度

当凹陷深度达到一定程度时，将会降低加筋板的整体横向刚度.由图4可知，凹陷深度达到58.878 mm时，无量纲应力应变曲线的斜率明显变小，表明其轴向刚度的降低.当碰撞发生于加强筋时，凹陷损伤对于轴向刚度的影响较大，由图7～8可知，凹陷深度为25 mm时，出现刚度的降低，这主要是由于碰撞发生于加强筋时，主要的凹陷损伤发生于翼板，但是腹板也会发生局部的变形，从而引起刚度的降低.

5 结 论

1) 含凹陷加筋板在单轴压缩载荷作用下会发生屈曲变形，极限强度值比完整加筋板小.这表明凹陷损伤(凹陷深度和凹陷面积)对加筋板极限强度有削弱作用；

2) 由于加强筋的刚度较大，相同重量、相同深度的碰撞引起的凹陷损伤小于板格.当同一重量、同一速度的球在撞击加筋板板格中间、翼板中间和板格所在加筋处中间3处位置时，在板格中间形成的凹陷深度最大，其对应的极限强度值也最小.这表明，3种凹陷位置，凹陷在板格中间时将会引起结构的板格屈曲，而凹陷位于翼板会引起结构的加筋侧倾屈曲，当凹陷位于板格和加筋连接处将会引起上述两种失效模式同时发生；

3) 碰撞凹陷损伤分别发生在板格(或是板格处与加强筋相连接)以及加筋处时，加筋板结构在轴向压缩载荷下将出现不同的失效模式.当凹陷深度达到一定程度时，将会降低加筋板的抗弯模量，使结构更容易发生屈曲.

[1]DOW R S, SMITH C S. Effects of localized imperfections on compressive strength of long rectangular plates[J]. Journal of Constructional Steel Research,1984,4(1):51-76.

[2]PAIK J K, LEE J M, LEE D H. Ultimate strength of dented steel plates under axial compressive loads[J]. International Journal of Mechanical Sciences,2003,45(3):433-448.

[3]PAIK J K. Ultimate strength of perforated steel plates under edge shearing loading[J]. Thin-Walled Structures,2005，43:1475-1492.

[4]LUIS R M, GUEDES SOARES C. Ultimate strength of plate assemblies with localized imperfection subjected to compressive loads[C].Proc 3rd European Conference on Computational Mechanics, Solids, Structures and Coupled Problems in Engineering, Lisbon, Portugal,2006.

[5]AN H, AN W G, ZHAO W T. Reliability analysis of ship structure system with multi-defects[J]. Sci China Physics, Mechanics & Astronomy,2010,53(11):2113-2124.

[6]RAVIPRAKASH A V, PRABU B, ALAGUMURTHI N. Ultimate strength of a square plate with a longitudinal transverse dent under axial compression[J]. Journal of Mechanical Science and Technology,2011,25(9):2377-2384.

[7]RAVIPRAKASH A V, PRABU B, ALAGUMURTHI N. Residual ultimate compressive strength of dented square plates[J]. Thin-Walled Structures,2012，58:32-39.

[8]RAVIPRAKASH A V, PRABU B, ALAGUMURTHI N. Effect of size and orientation of a centrally located dent on the ultimate strength of a thin square steel plate under axial compression[J]. International Journal of Steel Structures,2012,12(1):47-58.

[9]王智祥，王红梅.船与FRP浮箱非线性动力学碰撞过程的数值仿真[J].船舶力学，2013,17(5)：539-546.

[10]张婧,施兴华,顾学康.具有初始缺陷的船体加筋板结构在复杂受力状态下的极限强度研究[J].中国造船,2013(1):60-70.

[11]张婧,江小龙,石晓彦,等.具有初始缺陷的裂纹加筋板剩余极限强度分析[J].哈尔滨工程大学学报,2016,37(7):1-9.

Collapse Study of Stiffened Panel with Dent Induced by Impact

SHI Xinghua BAO Jun QIAN Peng BIAN Xuanyi

(SchoolofNavalArchitectureandOceanEngineering,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China)

In this paper, the dent is assumed to be formed by a ball impacting on the stiffened plate. Three typical dent positions are selected including the middle of plate, the middle of flange and the plate strengthened by stiffener. The deformation state of stiffened plate after impact is kept, and subsequently the stiffened plate is compressed gradually. The collapse process of the dented stiffened is studied. Finally, the ultimate strength is obtained. The influence of speed and weight of the impactor on the ultimate strength of stiffened panels is analyzed. The failure mode of stiffened plate and influence of dent depth on ultimate strength of stiffened plate are discussed. The results indicate that the dent would reduce the ultimate strength of stiffened panels, and the ultimate strength decreases with the increase the area and depth of depression. Compared with the dent in the middle of flange and the middle of stiffener, the influence to the ultimate strength of dented stiffened panel in the middle of the plate is the greatest. Different failure modes are investigated in dent stiffened plate under different impact positions subjected to compressive load.

stiffened panel; dent; ultimate strength; impact

2016-09-09

*国家自然科学基金项目(51509113)、江苏省高校自然基金项目(13KJA570001,14KJB580005)、江苏省重点实验室开放基金项目(CJ1403)资助

U661.1 doi:10.3963/j.issn.2095-3844.2016.05.005

施兴华(1981- )：男，博士，副教授，主要研究领域为船舶与海洋结构物的极限强度