多重四边形环索-张弦梁屋盖拉索张拉施工过程监测及数值模拟分析*

张 超 余 立 刘 涛

(福州大学土木工程学院 福州 350108)



多重四边形环索-张弦梁屋盖拉索张拉施工过程监测及数值模拟分析*

张 超 余 立 刘 涛

(福州大学土木工程学院 福州 350108)

为了研究四边环索-张弦梁屋盖在索力张拉时的变化规律，以福州奥体中心体育馆屋盖为工程背景，实时监测索力张拉过程中拉索索力、构件应变及屋盖变形等关键响应. 监测结果表明，张拉各重四边形环索可以使屋盖的挠度显著减小；然而，张拉张弦索，会产生一定的“卸载”作用，使得屋盖挠度略有增加，预应力张拉完成后，整个屋盖结竖向刚度显著增大，屋盖挠度减小124 mm.各阶段索力张拉过程中，索力及杆件应力均在安全许可范围内. 同时，建立空间有限元分析模型，定义非线性阶段施工工况，采用短链杆的温降收缩模拟实际各级索力张拉过程. 数值模拟结果与实测结果吻合较好，说明文中建立的数值模型可以较准确地模拟多重环索-张弦穹支屋盖在索力张拉过程中的响应.

多重四边环索；张弦梁；穹顶结构；索力张拉；施工监测

0 引 言

四边形环索弦支结构是一种新型结构体系，由网格梁、下撑钢管、斜索及四边形环索构成，通过斜索的预应力张拉，使下撑钢管承受压力，改善网格梁结构的受力和变形性能. 四边形环索弦支结构具有线条简单，用钢节约，传力明确的特点.已成功应用于在深圳北站雨棚的屋盖设计中[1].当结构跨度较大时，可以设置多重四边形环索，还可以再增设张弦索，以进一步提高屋盖的竖向刚度，即形成了复杂的多重四边形环索-张弦梁屋盖.此屋盖已被首次应用于福州奥体中心体育馆椭圆形屋盖的设计中.

由于预应力拉索数量众多，且位置各异，需要进行复杂的分批、分步、分级的索力张拉过程. 整个索力张拉过程屋盖体系受力变化十分复杂[2]. 然而，目前对于索力张拉的研究成果多集中于张弦梁和穹支结构[3].而对四边环索弦支结构在索力张拉中的变化规律研究较少，且仅局限数值模拟分析. 傅学怡等[4]基于数值模拟方法分析了深圳北站站台雨棚(单重四边环索结构)的索力张拉过程中屋盖结构的受力变化.至今为止，还未见到多重四边环索弦支屋盖在索力张拉时的数值分析和实测结果的研究.

为了研究多重四边形环索-张弦梁屋盖在索力张拉过程中的变化规律，文中以福州奥体中心体育馆屋盖为研究背景，分别开展索力张拉的施工过程监测及数值有限元模拟的研究工作，探讨索力张拉过程中多重四边形环索-张弦屋盖的受力变化规律.

1 工程背景

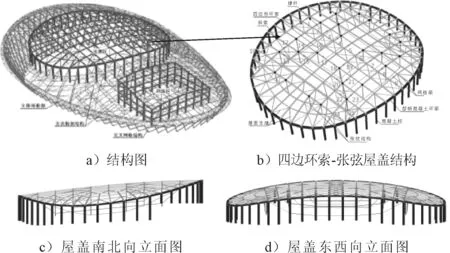
图1 福州奥体中心体育馆

福州奥体中心体育馆的侧立面图见图1a).该体育馆的屋盖根据跨度不同，分别采用三重环索-张弦梁结构和平面主次桁架结构. 其中综合比赛馆上空屋盖为椭圆形，为国内首次采用四边形环索弦支-张弦组合结构体系. 其跨度约97 m×116 m，周圈混凝土柱作为屋盖结构的内支座.

综合比赛馆上空四边形环索弦支-张弦组合结构体系结构三维视图见图1b)，南北向及东西向侧立面图分别见图1c)和图1d).此屋盖最高点标高39.7 m，张弦梁最大跨度75.9 m，环索弦支结构跨度106.5 m.整个屋盖系统主要由三重四边形环索、张弦结构和网格梁组成. 三重四边形环索的剖面见图2a).由于屋盖四边负荷面积较大，在东西两侧设置独立张弦结构(撑杆高度8.5，11.0 m)，增加结构竖向刚度，见图2b).拉索采用直径5 mm或直径7 mm高强钢丝组成的PE成品索，高强钢丝抗拔强度不小于1 670 MPa，弹性模量不小于195 GPa.拉索其他参数见表1.

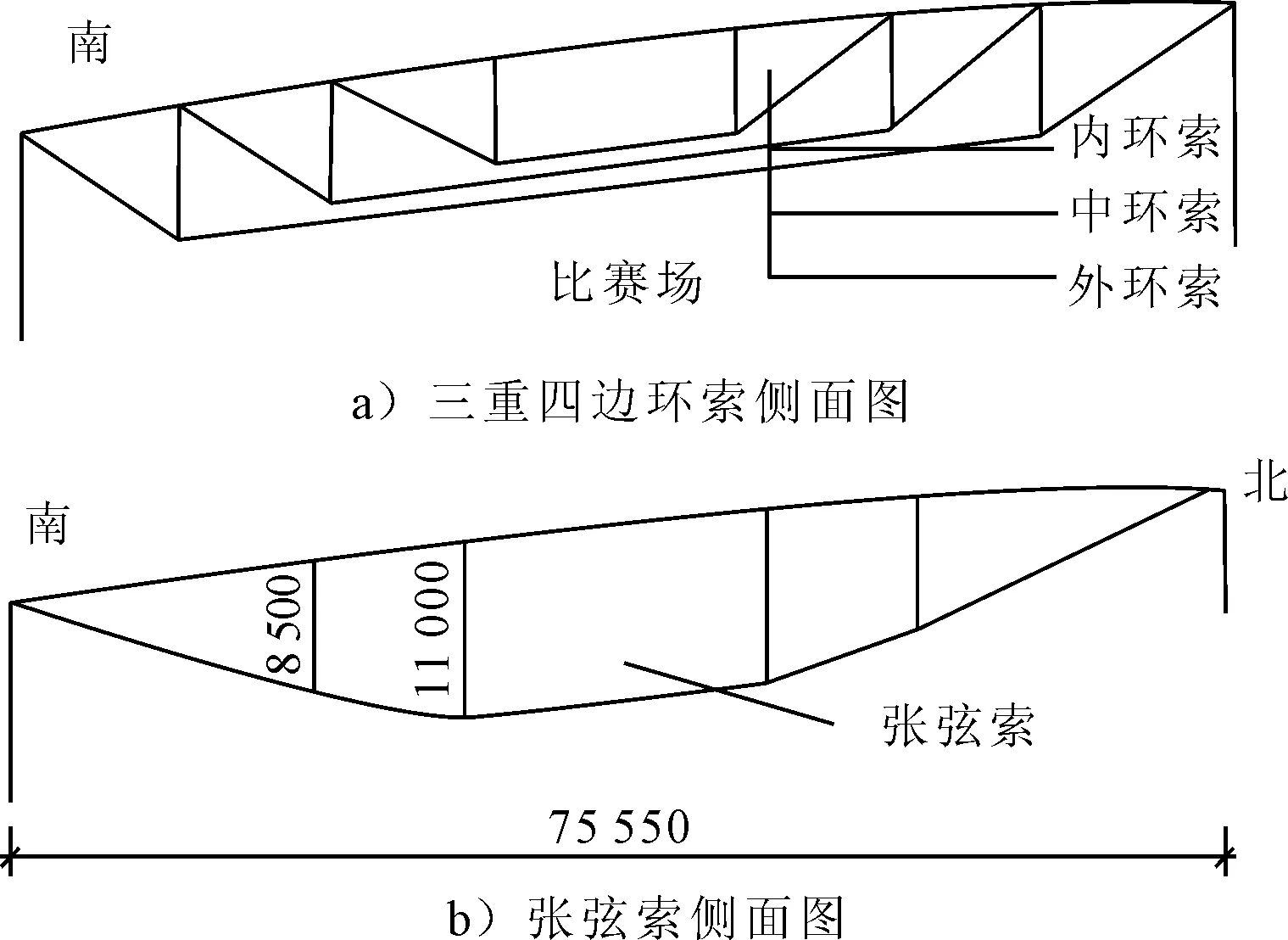
图2 拉索立面图

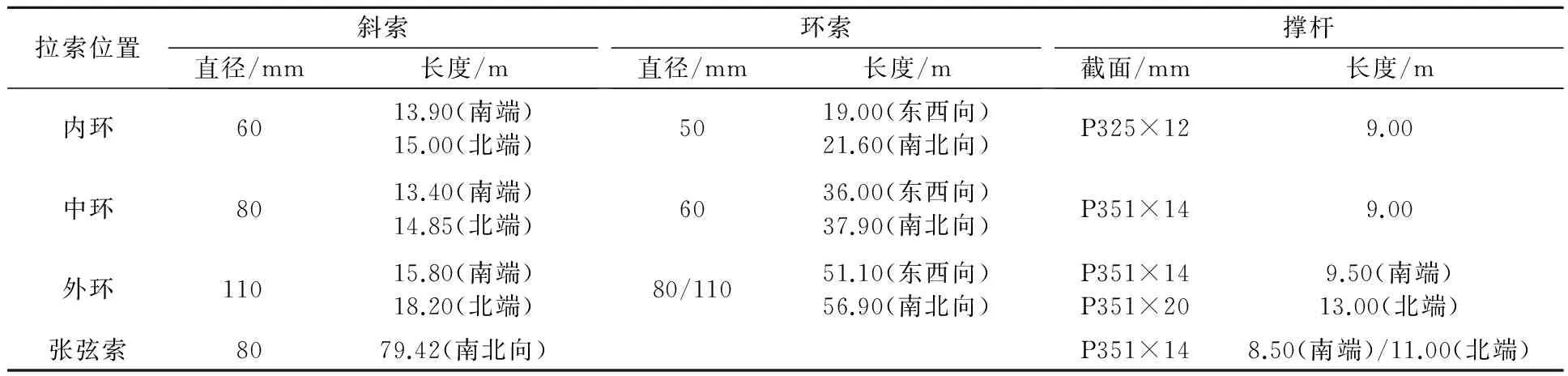
拉索位置斜索直径/mm长度/m环索直径/mm长度/m撑杆截面/mm长度/m内环6013.90(南端)15.00(北端)5019.00(东西向)21.60(南北向)P325×129.00中环8013.40(南端)14.85(北端)6036.00(东西向)37.90(南北向)P351×149.00外环11015.80(南端)18.20(北端)80/11051.10(东西向)56.90(南北向)P351×14P351×209.50(南端)13.00(北端)张弦索8079.42(南北向)P351×148.50(南端)/11.00(北端)

2 拉索张拉方案

本工程采用径向索张拉法，具体张拉方法为：对于四边环索，4根斜索同时张拉[5](见图4)；对于张弦梁索，采用一端张拉. 在背景工程中，每重环索的斜拉索及张弦索采用对称张拉. 由于各重环索及张弦索的不同张拉顺序会影响张拉过程中屋盖内力的变化[6].本工程中，基于张拉顺序优化分析结果：先张拉多重环索的斜索，再张拉张弦索，即采用“外环斜索—中环斜索—内环斜索—张弦梁拉索”的张拉顺序，见图3.

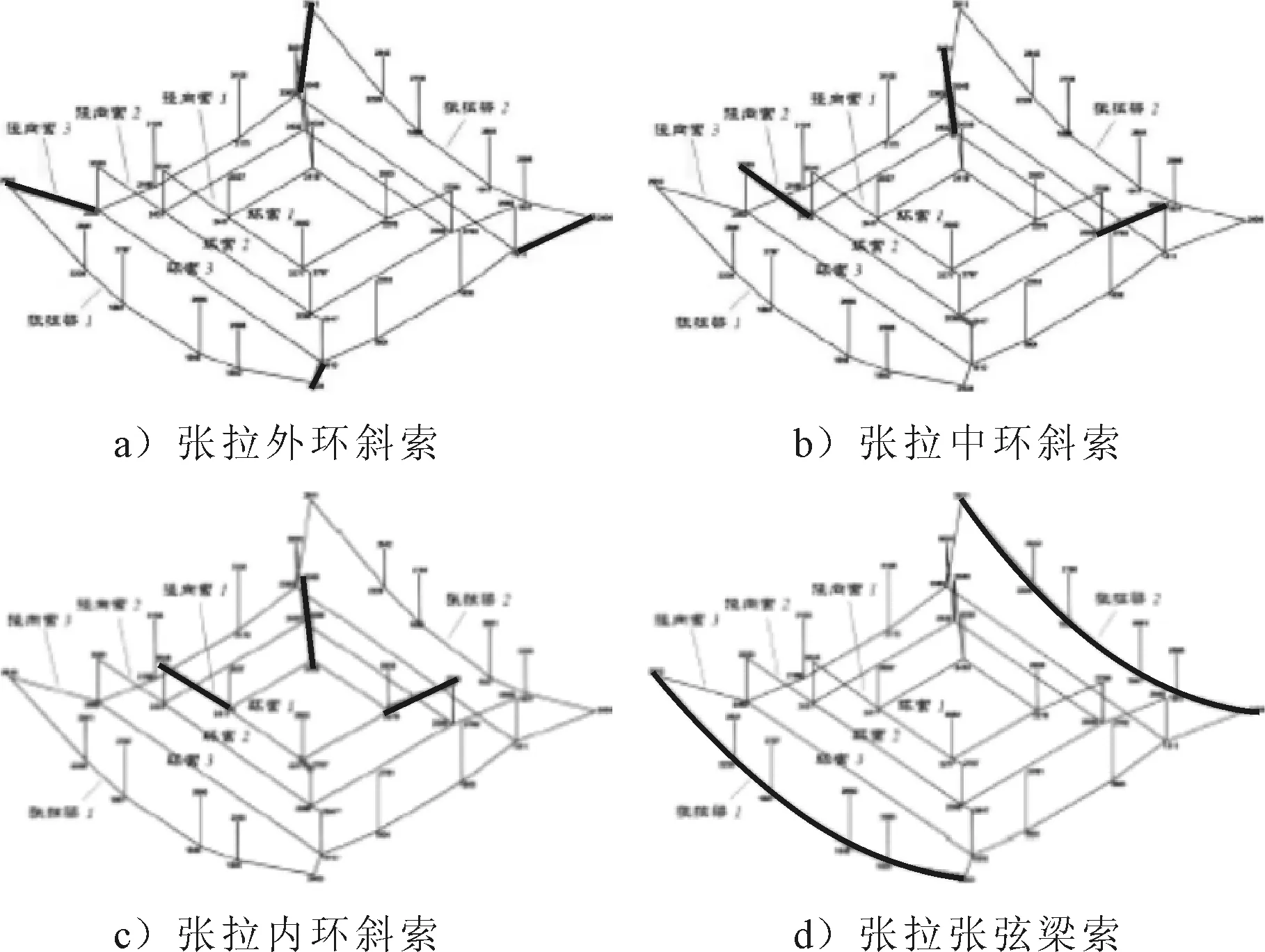
图3 张拉顺序示意图

为避免张拉过程中过大的超张拉，同时使索力增长梯度更为缓和，文中张拉施工总体分两级张拉，第一级为50%，第二级为100%.因此，共分为8个张拉步骤进行索力张拉.每个张拉步的张拉索力由倒拆法分析得到，具体数值见表2.在同级内又分3小步张拉，每步分别为50%，90%和100%.

但是，在实际张拉的过程中，第5步(张拉外环斜索)的预应力未能施加到位，仅张拉到设计索力值的80%左右.因此，在原计划的第7步和第8步之间进行外环斜索补充张拉，此张拉步骤号定义为第5(s1)步.因此，实际索力张拉施工共分为9个步骤进行.后文的数值模拟分析即按实际张拉步骤进行模拟.

根据设计的2级张拉步骤进行数值模拟，计算结果表明，最大张拉力为外环斜索，索力值为3 533 kN.因此选用2台2 500 kN千斤顶对其张拉，同步张拉4点，共计8台2 500 kN千斤顶.

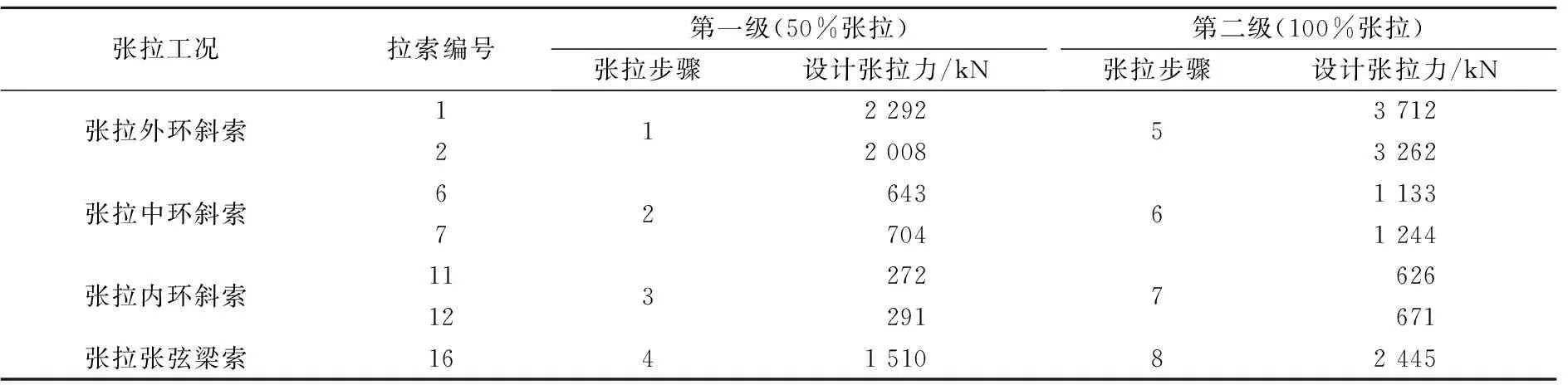
表2 设计索力张拉方案

3 索力张拉过程监测

根据该屋盖结构的特点，采用的索力、变形及应力监测方案如下.

1) 索力监测 由于此屋盖结构为沿南北中轴线的对称结构，张拉过程中对其中一侧的16根索进行监测，索力测点的布置见图4a).拉索索力监测采用频率法.

2) 变形监测 屋盖上共布置9个监测点. 自北向南标记为1～9号测点见图4b).

3) 应力监测 文中选取撑杆及与斜索相连的网格梁为关键杆件，选取的关键截面位置见图4d).测点布置在相应杆件的中间截面.采用振弦式应变计监测应变数据见图4c).

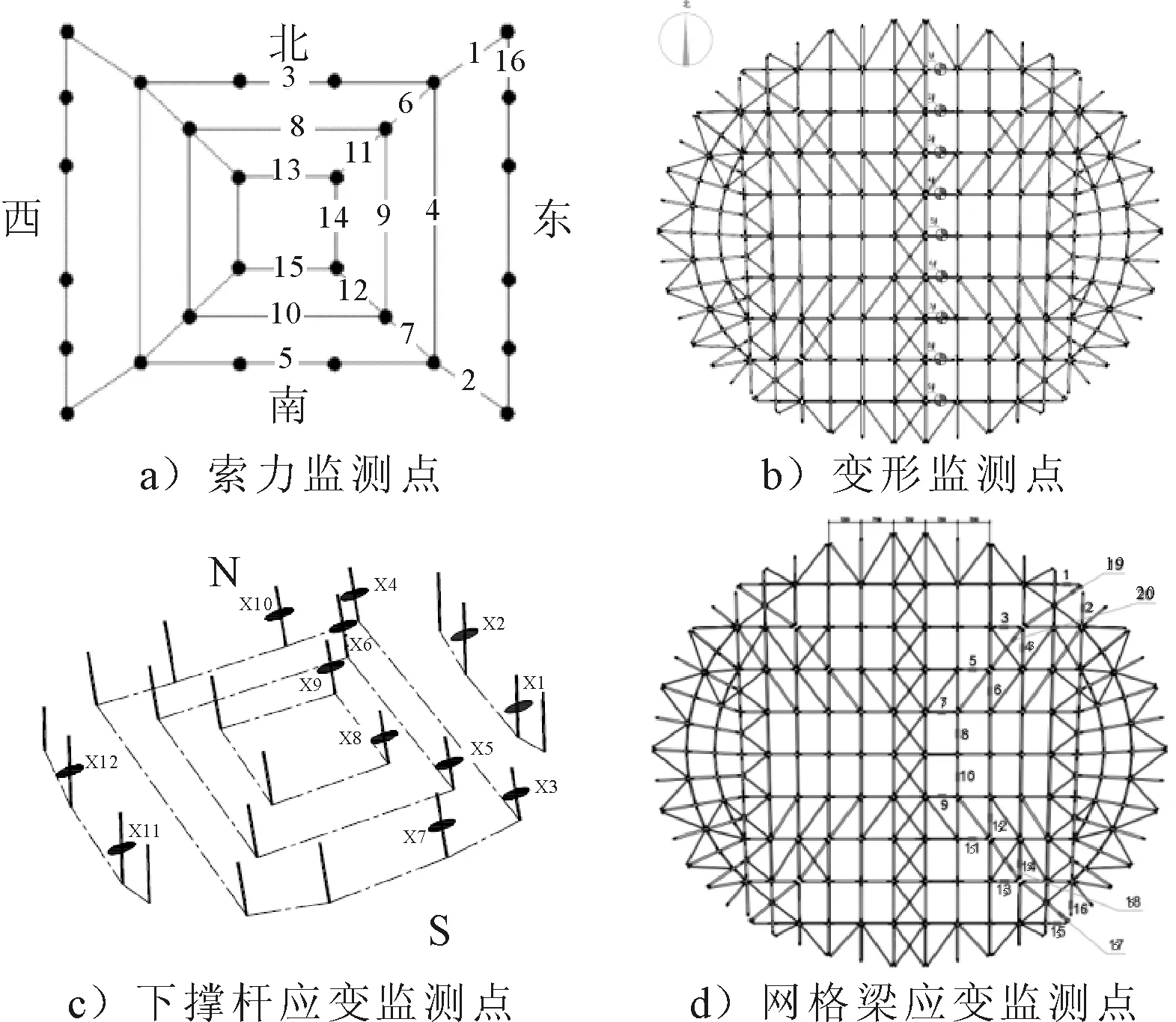
图4 监测测点布置图

4 拉索张拉的数值模拟

采用通用有限元软件SAP2000建立整体钢结构屋盖的三维有限元计算模型，见图5～图6.在数值模型中，四边环索-张弦梁屋盖结构中，网架梁为箱型截面，采用Frame单元模拟，钢弹性模量E=206 GPa，体密度取7.85×103kg/m3；预应力拉索采用Cable单元进行模拟，拉索弹性模量E=195 GPa，抗拉强度取1 670 MPa；撑杆采用Link单元模拟，从而保证在张拉过程中，撑杆上下两端可以自由转动；马道为该网架结构中的附属结构，在模型中仅考虑马道的自重(1.5 kN/m)，以分布质量形式施加于相应杆件上.网格梁最外层的环梁与劲性钢管柱耦合6个方向自由度，以模拟实际工程中固接连接.

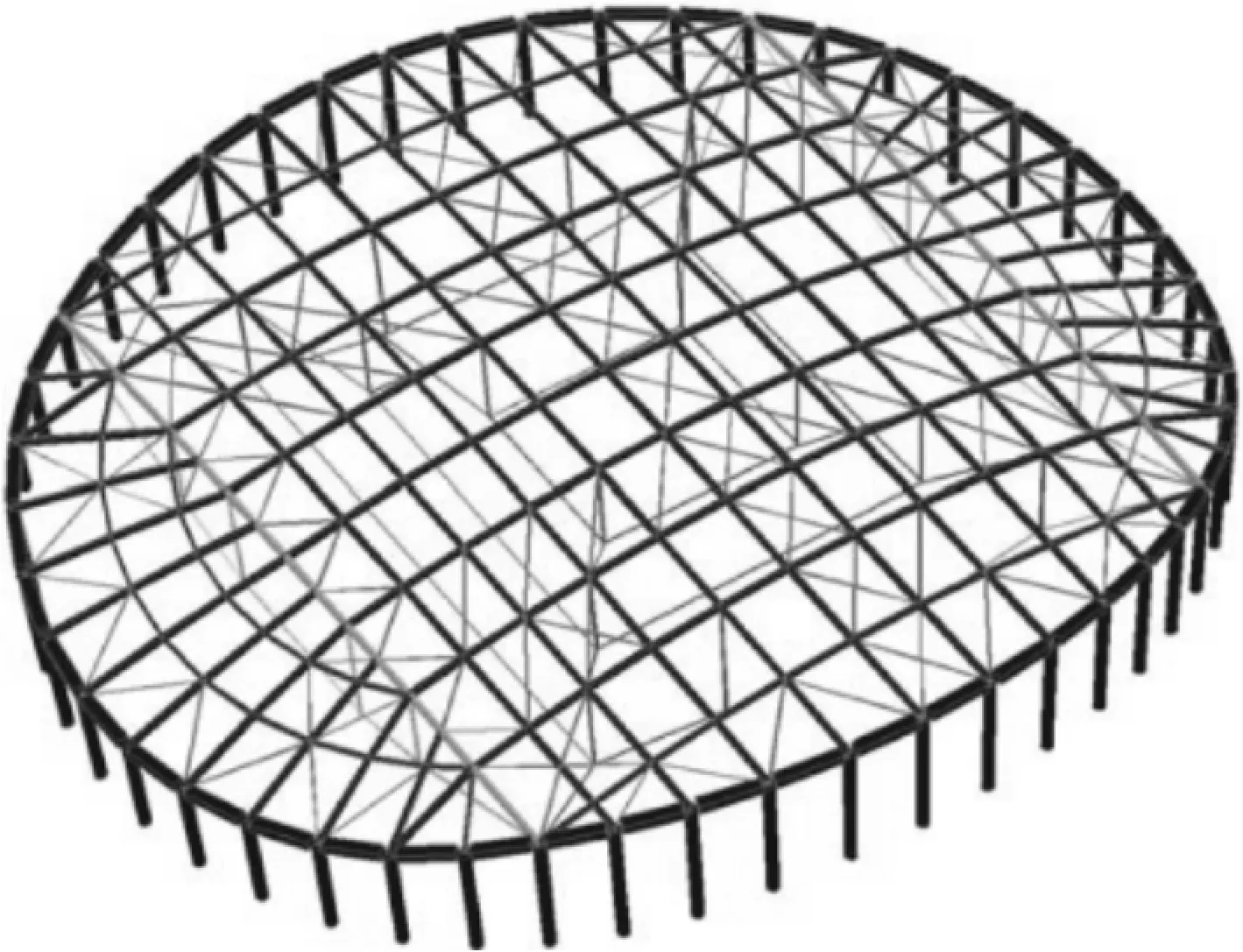
图5 三维有限元模型

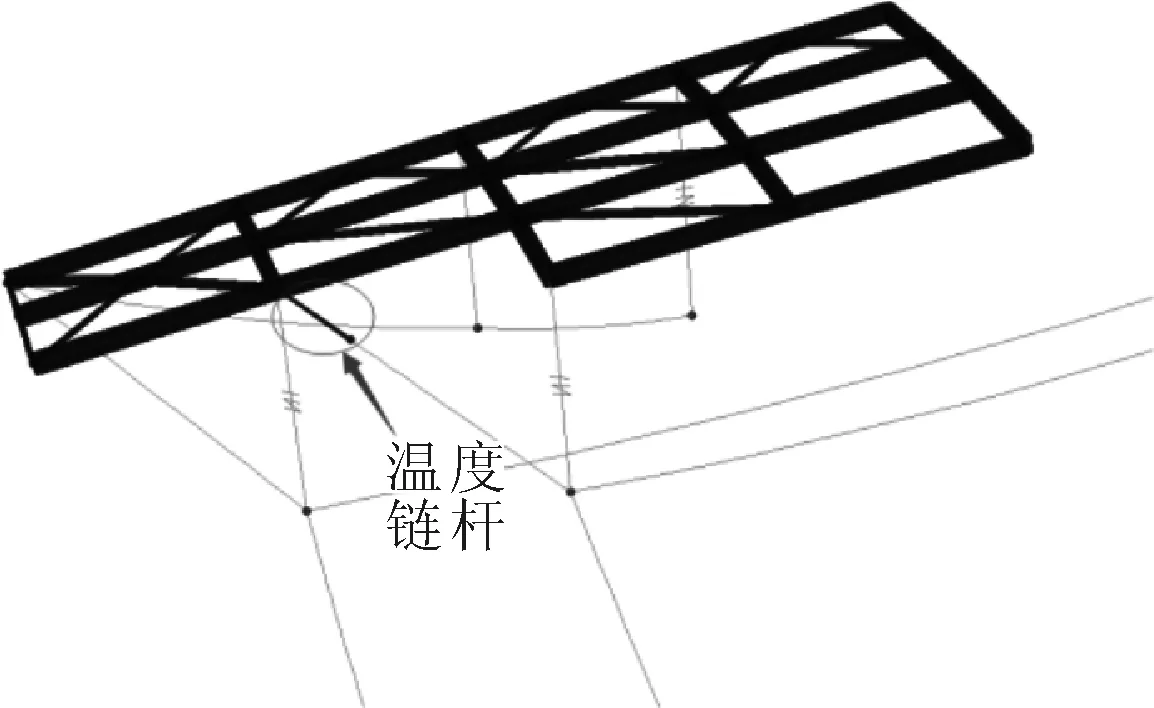
图6 拉索张拉模拟单元

索力张拉过程采用SAP2000中“非线性阶段施工”进行模拟.根据实际索力张拉顺序，把每一步索力张拉施工定义为一个施工阶段.文中在张拉索索端节点与锚固节点间设置一根具有一定温变系数的短链杆，通过该短链杆的温降收缩模拟千斤顶的张拉过程，见图7.各施工阶段的温降荷载以实际施工中油压表实测张拉力计算得到.

5 实测数据及数值结果分析

5.1 拉索索力变化

拉索是此空间张弦结构的重要组成部分，因此施工过程中拉索的反应也尤为重要，以下列出第二级(100%张拉)张拉施工影响较大的拉索索力值，见表3.表3中，实际张拉值为拉索张拉装置(千斤顶)的油压表读数换算值；实测索力值则为基于拉索实测频率，采用文献[7-8]中考虑抗弯刚度影响的实用公式的计算值；数值计算值为上文所建立的数值计算模型分析得到的索力值.

比较张拉斜索的实际张拉值和实测索力值可以发现，对于外环、中环斜索及张弦索，文中基于频率法的实测索力值与油压表测量的索力值吻合较好. 但是，对于内环斜索(11，12号斜索)，两者误差较大，约为10%，其主要原因可能是内环斜索长度较短，且拉索应力值较低，使得采用文献[9-10]中公式的计算索力存在一定的误差. 文中还对受张拉斜索影响较大的环索索力进行监测，如第6步张拉后，8号环索索力仅为591 kN，拉索应力程度较小.整个张拉过程中，索力最接近破断荷载的为16号张弦梁拉索，其施工过程中索力最大值仅为破断荷载的17%. 索力监测结果表明在拉索张拉施工全过程各索力均远小于相应的破断荷载，此屋盖中拉索受力是安全的.

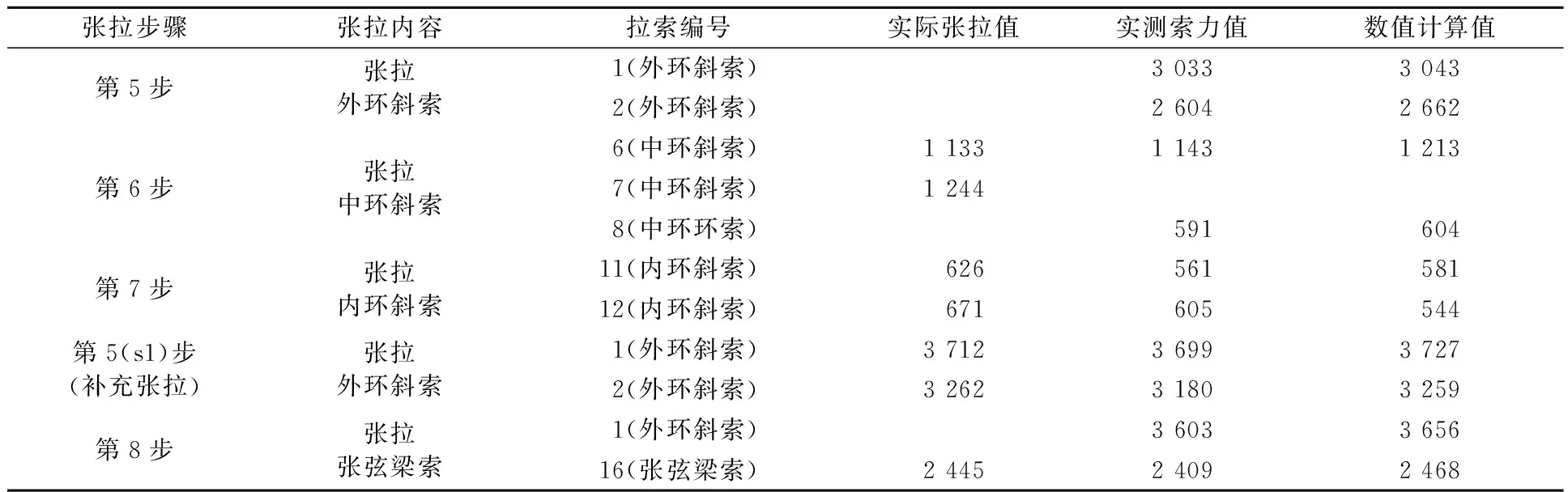
表3 各级张拉施工下拉索索力值 kN

表3还比较了数值模拟计算得到的各拉索索力值. 计算索力值与实测索力值较为接近，最大误差也是出现在第7步张拉时的12号索，误差值-10%.其它索力误差均在6%以内.

5.2 屋盖竖向变形

图7列出位移较大的2#,3#,4#,5#节点在张拉全过程中竖向变形图.以张拉前的屋盖位置为变形零点. 由图7可知，随着各级索力张拉，屋盖结构各关键节点位移向上增大，整个屋盖结构起拱变化趋势，表明在在预应力作用下屋盖结构竖向变形整体提升. 各级张拉结束后，累积向上变形测量值分别为99，124，121，101 mm，最大变形为3#测点. 然而，监测结果表明，在各级张拉过程中，屋盖竖向变形并非线性提升.在各重环索张拉时(第1～3级，第5～7级张拉)，屋盖各关键节点竖向位移随着张拉施工持续上升；但是当张拉两侧张弦索时(如第4级，第8级张拉)，屋盖各节点位移不提升反而下降.此位移变化规律对于更靠近中央的节点(如4#,5#)，更为明显. 就5#节点的实测值而言，第1～3级张拉后，该节点向上变形65 mm；第4级张拉后，该节点向下变形12 mm.这是因为该屋盖中，张弦梁分布在三重环索的外围，距离屋盖中心较远. 张拉张弦索的张拉施工后，会导致张弦梁撑杆间网格梁的整体向上变形(起拱)，从而引起其中间各环索应力的松弛，产生部分预应力损失. 越靠近中央的屋盖节点，预应力损失的越显著. 在内环间的屋盖节点(如5#节点)，则会受到三重环索预应力损失的影响，因此，张弦梁张拉对引起的位移损失最明显，如第8级加载下，其向下位移21 mm.

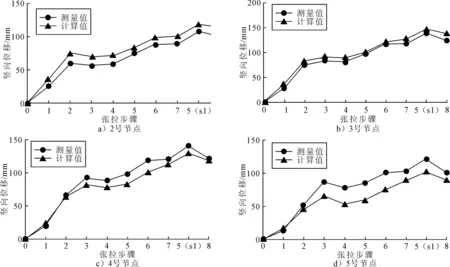
图7 屋盖结构关键节点竖向位移变化图

实测各节点竖向变形规律也得到数值分析结果的验证.总体来看，测量值与计算值的变化趋势吻合良好，数值相差也较小，每一步的竖向位移变化均较为接近，竖向位移最大差值为5号节点，最大位移差出现在第3级张拉时，约为12 mm.可能是因为实际预应力张拉过程中存在温度变化等影响因素，而数值模型中则未考虑.

5.3 网格梁应力变化

由于网格梁中杆件众多，鉴于篇幅的原因，文中仅列出其中关键杆件的响应结果，见图8. 其中1#测点位于与外环斜索相连的网格梁中间截面，3#测点位于与中环斜索相连的网格梁中间截面.由图可以看出，当外环斜索张拉时，1号测点所在杆件截面轴压力增大，因此1#测点的应变值显著减小，如第1级，第5级，第5(s1)级张拉，而其他的拉索张拉则对1#测点的应变影响不大. 同理，当中环斜索张拉时(第2级，第6级)，中环斜索张拉导致该3#测点所在杆件的轴压力明显增大，3#测点的应变值也显著降低.

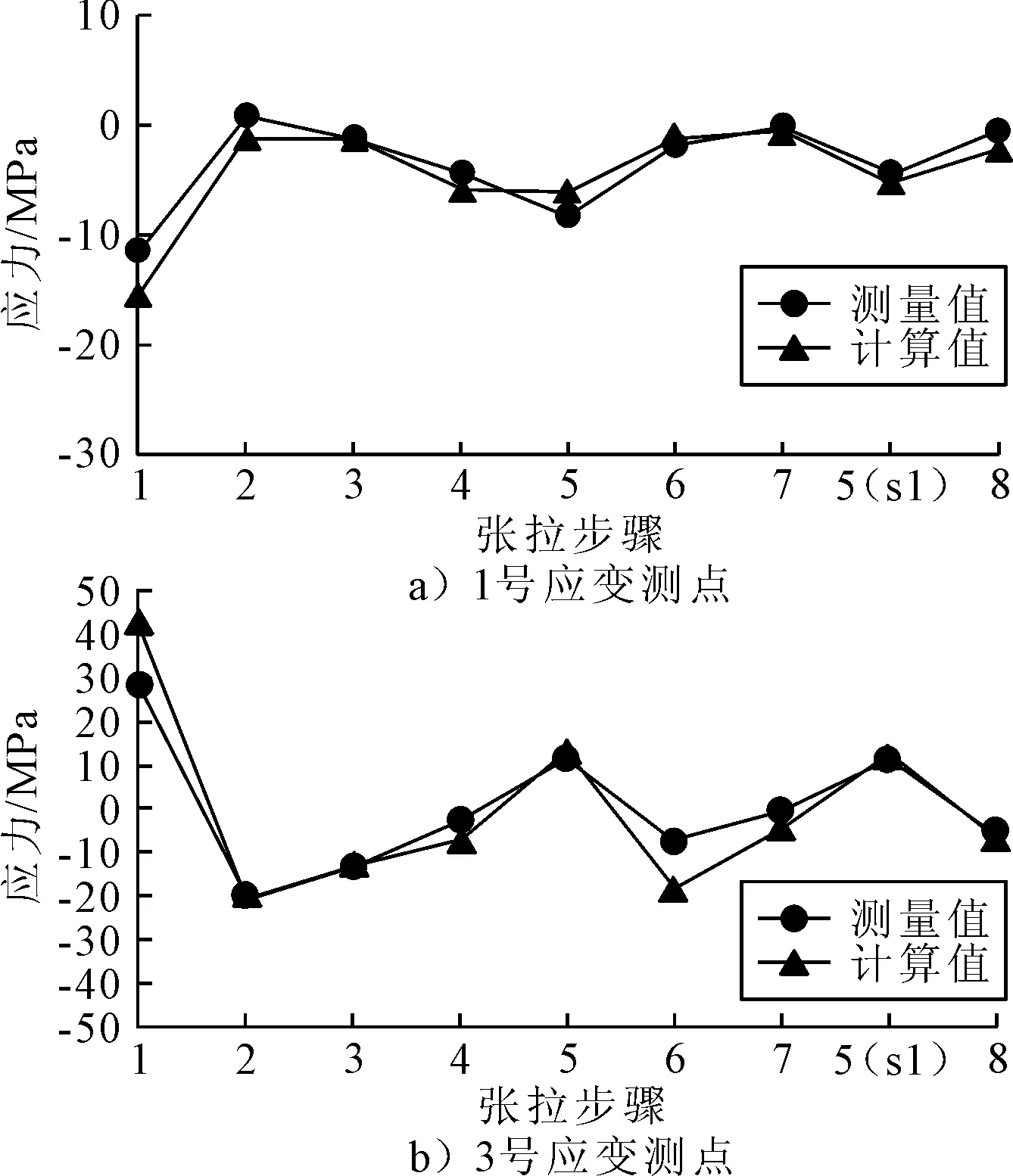
图8 网格梁截面应力变化图

由测量结果与计算值对比可以看出：施工张拉过程中，网格梁应力的测量值与有限元计算值存在一定的误差，但变化趋势基本一致，均远小于杆件应力设计值，杆件处于较低的应力水平，因此，整个施工过程中网格梁结构始终处于安全的受力状态.

6 结 论

1) 通过对各级拉索张拉过程的屋盖结构关键截面的受力及变形进行监测. 监测结果表明，按照设计的“先环索，后张弦索”的张拉方案，屋盖变形及关键构件受力均变化均匀，最大值均未超过规范要求，且具有一定的安全储备，满足施工安全的要求.

2) 不同张拉阶段的监测数据表明：各级环索的预应力张拉可以显著增加屋盖结构竖向刚度，使屋盖挠度显著减小；然而，张弦索的张拉则会产生一定的“卸载”作用，使得屋盖挠度增加.但是，全部拉索预应力张拉后，整个屋盖结竖向刚度显著增大，屋盖竖向挠度提升124 mm.

3) 数值模拟值与实测数据吻合较好，说明文中采用降温法可以较精确地模拟拉索预应力张拉全过程，文中建立的数值模模型可以较准确地模拟多重环索-张弦穹支屋盖结构的受力.因此，文中数值模型可以为后续结构健康监测、抗震及抗风研究提供基准数值分析模型.

[1]陆赐麟，尹思明，刘锡良.现代预应力钢结构[M].北京：人民交通出版社，2003.

[2]陈志华，弦支穹顶结构体系及其结构特性分析[J].建筑结构，2004,34(5)：38-41.

[3]季晗，熊世树，黄丽婷，等.弦支穹顶拉索张拉过程现场监测与数值模拟[J].武汉理工大学学报，2008，30(9)：93-97.

[4]傅学怡，孙璨，吴兵，等.深圳北站站台雨棚新型弦支结构体系设计[J].建筑结构，2015,45(1):47-52.

[5]刘红波，陈志华，牛犇.弦支穹顶结构施工过程数值模拟及施工监测[J].建筑结构学报，2012,33(12)：79-84.

[6]孙璨，傅学怡，吴兵，等.深圳北站站台雨棚新型弦支屋盖张拉模拟及试验研究[J].建筑结构，2015,45(1)：52-57.

[7]王化杰，范峰，钱宏亮，等.巨型网格弦支穹顶预应力施工模拟分析与断索研究[J].建筑结构学报，2010，42(1):247-253.

[8]石开荣，郭正兴，罗斌.环形辐射状预应力张弦梁钢屋盖张拉优化[J].东南大学学报(自然科学版)，2015,35(1):55-60.

[9]任伟新，陈刚.由基频计算拉索拉力的实用公式[J].土木工程学报，2005，38(11)：26-31.

Construction Monitoring and Numerical Simulation of Multiple Square Loops-string Dome

ZHANG Chao YU Li LIU Tao

(CollegeofCivilEngineering,FuzhouUniversity,Fuzhou350108,China)

In order to study the mechanical characteristic of Multiple Square Loops-String Dome (MSLSD), Fuzhou Olympics Gymnasium is taken as the research background in this paper, which is the first MSLSD project in China. Tension force, sections stress and displacement of the MSLSD under each construction process are monitored. The measured data indicate that tensioning cables of Square Loops can reduce the deflection significantly and improve vertical stiffness of roof. However, the tensioning cables of beam strings increase the roof deflection slightly, which acts as unloading effect. In the end, the vertical stiffness of MSLSD roof increases significantly, and vertical deflection is enhanced by 124 mm after all prestress constructions. For each prestress construction stage, the construction monitored values of cables tension forces and sections stresses are within the safety range. Meanwhile, the 3D finite-element model of MSLSD is established. In the model, the prestress constructions are simulated by temperature shrinkage of special link elements. The numerical results match well with monitor data, which validates the numerical model.

multiple square loops (MSL); beam string; dome; prestress construction; construction monitoring

2016-08-01

*国家自然科学基金项目(E51508102)、教育部博士点基金项目(2013351420006)、福建省教育厅科技基金项目( JK2014005)资助

TU356 doi:10.3963/j.issn.2095-3844.2016.05.008

张超(1985- )：男，博士，副教授，主要研究领域为大跨度结构及抗震性能