基于投资者情绪的均值-方差投资组合选择研究

罗 琰 刘晓星

( 1.南京审计大学 金融数学系，江苏 南京 211815；2.东南大学 经济与管理学院，江苏 南京 211189)



基于投资者情绪的均值-方差投资组合选择研究

罗 琰1,2刘晓星2

( 1.南京审计大学 金融数学系，江苏 南京 211815；2.东南大学 经济与管理学院，江苏 南京 211189)

将投资者情绪引入投资组合选择问题研究，构建了投资者情绪调节的均值-方差投资组合模型，通过拉格朗日乘数法，得到了最优投资组合策略及有效前沿的解析解，结果表明：最小情绪调节方差在达到最小值点前随投资者情绪的增加而递减，之后随投资者情绪的增加而递增，呈现出一种U型的抛物线关系；在方差-均值坐标中有效前沿与经典的均值-方差模型的有效前沿形状是一致的，但投资者情绪函数越大，有效前沿越向方差-均值坐标的右上端移动。

投资者情绪；均值-方差；投资组合；有效前沿

一、理论综述

传统金融学认为市场是有效的、信息是充分的，与资产相关的所有信息都能充分反应在价格中，主张投资者具有完全理性，会以效用最大化作为决策的依据，能对市场做出正确的无偏估计。然而，金融市场异象对占据金融学统治地位的有效市场假说(EMH)提出了严重的挑战。在金融市场上，存在大量非理性投资行为，投资者并非完全根据信息，而可能根据噪声(noise)进行交易，投资者情绪也是影响投资者行为的重要因素。De Long et al. (1990)[1]构建的噪声交易DSSW模型是研究投资者情绪和噪声交易对金融市场资产定价和投资决策影响的最具有代表性的理论模型，文章指出在有限套利的市场中, 如果投资者情绪相互影响，套利者将无法消除非理性行为导致的资产误定价，投资者情绪成为影响股票均衡价格的系统因子。

自De Long et al. (1990)研究工作后，国内外学者分别从多个视角研究了投资者情绪在金融市场的作用：其一，研究投资者情绪与股票收益之间的关系。如Brown and Cliff (2004)[2]实证研究了投资者情绪与短期股票收益率之间的互动关系，发现情绪和近期市场收益都是相关的，股票市场近期历史收益率和投资者情绪水平本身是情绪的重要解释变量，但情绪对市场短期未来收益预测能力很弱。Baker and Wurgler (2006)[3]认为投资者情绪对不同股票具有显著的横截面效应(Cross-section Effects)，股票的估值具有很强的主观性，而且难以套利。Zhong et al. (2015)[4]利用面板分位数回归模型研究了投资者情绪对中国A股上市公司股票市场收益率的非线性效用。王美今和孙建军(2004)[5]揭示投资者情绪是影响股票均衡价格的系统性因子，检验了投资者情绪与收益及收益波动的关系，发现投资者情绪变化不仅显著地影响沪深两市收益,而且显著地反向修正两市收益波动性，并通过风险奖励影响收益。蒋玉梅和王明照(2010)[6]以1997-2008年在深沪两市上市的一般上市公司A股为样本,探讨了投资者情绪对股票收益的总体效应(Aggregate Effects)与横截面效应，其结果表明，就总体效应而言，情绪与短期市场收益正相关，与长期市场收益负相关，说明投资者情绪对于股票收益产生系统性影响，但是就横截面效应而言，不同企业特征的股票收益对于情绪的敏感度存在差异。其二，实证研究投资者情绪与企业投资决策的关系。投资者的情绪可能会通过理性迎合渠道，股权融资渠道以及管理者乐观主义中介效应渠道影响企业的投资行为。如花贵如等(2011)[7]提出并证实了投资者情绪影响企业投资行为的管理者乐观主义中介效应渠道。崔晓蕾等(2014)[8]从过度投资的视角研究了投资者情绪对企业资源配置效率的影响，其结果表明在中国市场上投资者情绪对公司过度投资有显著的正向影响。张前程和杨德才(2015)[9]考察了投资者情绪对企业投资行为的影响，以及货币政策对投资者情绪与企业投资行为关系的影响，发现投资者情绪对企业投资规模具有正向影响，货币政策宽松度提高能够强化投资者情绪对企业投资规模的影响。其三，研究投资者情绪对资产定价的影响。如Yang et al. (2012)[10]构建了静态情绪资产定价模型，其结论表明投资者情绪对风险资产定价有系统性的重要影响，投资者情绪是资产定价的一个非线性系统因子，乐观的投资者具有较高的认知价格，而悲观的投资者具有较低的认知价格。Yang and Zhang (2013)[11]构建了异质投资者情绪的动态资产定价模型，异质情绪减少了财富分布的波动性和股票回报的均值回复性，但增加了股票回报的波动性。王博(2014)[12]构建了基于投资者情绪的资产定价理论模型，指出投资者情绪风险因子是资本资产定价模型的风险因子，需要对受投资者情绪影响的股票补偿额外情绪风险溢价。

然而，直接研究投资者情绪对最优均值-方差投资组合影响文献非常少。投资组合是金融学术研究的一个重要主题。经典均值-方差投资组合选择问题来源于Markowtiz (1952)[13]的起源性工作。Markowtiz模型的主要思想是,在可获得的金融资产中构造一个最优的财富配置策略，以使得在均值所刻画的期望收益和方差所刻画的风险之间达到最优平衡。罗琰等(2015)[14]研究了跳-扩散市场下的均值-方差投资组合问题。Fu et al. (2015)[15]提供了一个检验投资者情绪对均值-方差权衡的影响的理论框架。不过他们没有分析投资者情绪对最优投资组合决策及有效前沿的作用机制。陈其安等(2012)[16]以投资者效用最大化为决策目标，建立基于投资者情绪的投资组合模型，从理论上研究投资者情绪对投资组合结构及其收益-风险关系的影响。谢军等(2012)[17]基于投资者情绪构建了含有无风险资产的投资组合模型，并给出了模型的解析解及有效边界方程。但是上述文献都是直接给出投资者情绪影响均值或者方差，没有将均值和方差放在一个统一的均值-方差模型框架。实际上，投资者情绪的存在会直接影响投资者对风险资产将来平均回报率的判断，进而影响到投资者组合的方差。谢军和杨春鹏(2012)[18]构建了基于情绪认知的最优行为投资组合模型，在卖空约束条件下，得到了基于情绪的投资组合分析范式，但未能得到最优策略的解析解。

综合来看，多数文献只是从实证角度研究了投资者情绪与股票市场收益之间的关系，没有从理论上分析投资者情绪对投资组合结构以及收益与风险关系的作用机制。从理论上构建模型，分析投资者情绪对金融资产收益及波动特征的影响以及对最优投资决策影响的学术研究还非常欠缺。基于此，笔者将投资者情绪引入投资组合问题研究，在投资者情绪调节的均值—方差统一的框架下，研究投资者情绪对最优投资决策的影响，分析投资者情绪对情绪调节均值-方差有效前沿的作用。

二、模型建立及结论

1、模型的建立

(1)

称为投资组合的情绪调节平均期望收益率。

记σij=cov(Ri,Rj),i,j=1,2,…,n，称n阶矩阵∑=(σij)n×n为收益率-协方差阵。因此，情绪投资组合w=(w1,w2,…,wn)′的情绪调节收益率方差为：

(2)

实际上，还可以假设投资者对不同的风险资产具有不同的情绪参数s。此时，情绪函数为f(si),i=1,2,…,n。从行为金融学的观点来看，比如投资者具有证券投资本地化偏差，投资者持续显著地表现出购买本地证券的情绪偏好。但这不会影响笔者的主要结论，故笔者假设投资者对任何风险资产的情绪都是一致的。

假设投资者的目标是找到一个可行投资组合策略w*，使得情绪调节平均期望收益满足E(Rw)=μ，这里μ是一个给定的常数。同时，最小化投资组合的情绪调节方差(风险)，即情绪调节均值-方差投资组合选择问题。于是，上述最小方差投资组合可表述为如下最优化模型：

(3)

s.t.I′w=1

(4)

E(Rw)=w′f(s)E(R)=μ

(5)

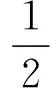
2、模型的结论

不妨记A=I′∑-1E(R),B=E(R)′∑-1E(R),C=I′∑-1I,D=BC-A2

(6)

通过拉格朗日乘数法，最优化模型(3)-(5)容易得到求解,可得到如下结论：

定理1 当投资者的预期平均期望收益率为E(Rw)=μ时，基于投资者情绪的最优投资组合策略为：

(7)

最小情绪调节方差为：

(8)

由式(7)可以看到，最优投资策略受到投资者情绪的作用，若投资者情绪函数f(s)=1时，则式(7)就可以化为经典无投资者情绪时Markowitz均值-方差模型的最优投资策略[19]。由式(8)可以看到，在方差-均值空间中，最小情绪调节均值-方差前沿仍然是具有二次形式的抛物线，若投资者情绪函数f(s)=1时，也可化为经典Markowitz均值-方差模型的有效前沿曲线方程。下一节，笔者将通过数值算例和作图进一步分析定理1的结论，给出其直观经济学解释。由式(8)变形可得

(9)

(10)

(11)

式(11)被称为全局最小情绪调节方差投资者组合策略。结合式(7)和式(11),可以得到如下的情绪调节两基金分离定理。

定理2 (两基金分离定理)当投资者情绪调节平均期望收益率E(Rw)=μ时，任意最小情绪方差投资组合wμ都可以唯一地表示为全局最小情绪调节方差投资组合ws和一个可分散化资产组合wd的组合，即有：

wμ=αsws+αdwd

(12)

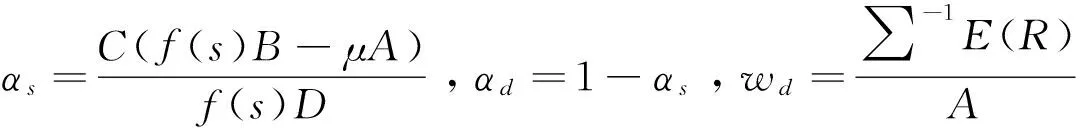
(13)

通常称ws和wd为共同基金。因此，由式(12)知，对于期望收益率μ，可以通过持有ws和wd的组合实现。

三、数值算例及经济学解释

1、数值算例

本节给出一个数值例子阐述第二节的结论，给出结论的经济学解释。笔者所有的计算都是利用软件Matlab R2013a完成。不妨设金融市场存在三种风险资产[19]，无投资者情绪时，各资产的期望收益率为E(R)=(0.1,0.15,0.2)′，协方差矩阵分别为：

表1给出了四种不同投资者情绪函数f(s)值和情绪调节平均期望收益率μ值情形下的最优投资组合策略以及相应的最小方差，也给出了对应的全局最小方差点(顶点)。

表1 投资者不同情绪和平均期望回报的最优投资策略及方差

2、结论的经济学解释

利用Matlab软件，做有关情绪调节方差与投资者情绪图，以及情绪调节方差-均值有效前沿图，可以更直观的展示模型隐含的规律，而且给出规律的经济学解释。各基本参数与上文相同。

图1 方差-投资者情绪曲线

图2 情绪调节均值-方差有效前沿

由图1可知：投资者情绪与最小情绪调节方差是一条U型的抛物线。当情绪调节平均期望收益率μ一定时，最小情绪调节方差最初随着投资者情绪函数f(s)的增加而递减，达到最小值后，则随着投资者情绪函数f(s)的增加而递增。当投资者情绪函数f(s)较小时，金融市场往往处于人气不足的相对理性时期，市场随着人气的增加而使流动性增加，进而减少金融市场萎缩带来的金融资产价格下跌的风险。当投资者情绪函数f(s)较大时，金融市场往往处于人气高涨上升时期，市场也会随着人气的增加而使流动性增加，但随着市场的进一步亢奋，资产的价格会不断上涨，脱离其基本价值，不可避免形成金融资产泡沫，从而使投资者面临更大的风险。从另外一个角度来看，在投资者情绪函数f(s)确定且较小时(如图小于0.8时)，金融市场处于人气不足时期，投资者情绪调节平均期望收益率小，则情绪调节方差也小，即收益和风险是对等的(μ小，则σ小)。但是，当投资者情绪函数f(s)确定且较大时(如图大于1.2时)，金融市场处于人气旺盛时期，投资者常常会高估投资收益，低估投资风险，因而呈现出低风险-高收益的特征(μ小，而σ大)。

四、结语

笔者在现有相关文献研究基础上，假设投资者情绪函数为情绪的非负递增函数，同时作用于投资组合的平均期望收益率以及方差，建立了情绪调节均值-方差投资组合模型。通过拉格朗日乘数法，得到了情绪调节的最优投资组合决策以及最小方差的显示解，而且还给出了情绪调节的两基金分离定理。若投资者情绪函数f(s)=1，则笔者的结论就是经典的Markowitz均值-方差投资组合模型。笔者的结论表明，最小情绪调节方差随投资者情绪的变大先递减后递增，呈现出一条U型的抛物线。最小情绪调节方差-均值坐标中有效前沿图形是一条向右开口的抛物线，但投资者情绪函数f(s)越大，模型的有效前沿越靠方差-均值坐标的右上端，即投资者情绪会同时放大期望收益率与方差；反之，则越靠近左下端，同时缩小期望收益率与方差。

[1]De Long J. B., Shleifer, A., Summers, L., Waldmann, R. J. Noise trader risk in financial markets [J]. Journal of Political Economy, 1990, (4): 703-738.

[2]Brown G. W., M. T. Cliff. Investor Sentiment and the Near-term Stock Market[J]. Journal of Empirical Finance, 2004, (1): 1-27.

[3]Baker M., J. Wurgler. Investor Sentiment and the Cross-section of Stock Returns[J]. The Journal of Finance, 2006, (61): 1645-1680.

[4]Zhong X., Wang D., Xue W. Investor sentiment and its nonlinear effect on stock returns—New evidence from the Chinese stock market based on panel quantile regression model [J]. Economic Modelling, 2015,(50):266-274.

[5]王美今, 孙建军. 中国股市收益、收益波动与投资者情绪[J].经济研究,2004,(10):75-83.

[6]蒋玉梅, 王明照. 投资者情绪与股票收益：总体效应与横截面效应的实证研究[J].南开管理评论,2010,(3):150-160.

[7]花贵如, 刘志远, 许 骞. 投资者情绪、管理者乐观主义与企业投资行为[J]. 金融研究,2011,(9):178-191.

[8]崔晓蕾, 何 婧, 俆龙炳. 投资者情绪对企业资源配置效率的影响——基于过度投资视角[J].上海财经大学学报, 2014,(3):86-94.

[9]张前程, 杨德才. 货币政策、投资者情绪与企业投资行为[J].上海财经大学学报, 2015,(12):57-68.

[10]Yang C., Xie J., Yan W. Sentiment capital asset pricing model [J]. International Journal of Digital Content Technology and its Applications, 2012, (3): 254-261.

[11]Yang C., Zhang R. Dynamic asset pricing model with heterogeneous sentiments [J]. Economic Modeling, 2013, (33):248-253.

[12]王 博. 基于投资者情绪的资产定价理论及实证研究[J].北京工商大学学报, 2014,(3):89-97.

[13]Markowitz, H. M. Portfolio selection [J]. Journal of Finance, 1952, (1): 77-91.

[14]罗 琰,杨招军,张 维. 跳扩散市场投资组合研究[J].经济数学,2013,(3):107-110.

[15]Fu C., Jacoby G., Wang Y. Investor sentiment and portfolio selection [J]. Finance Research Letters, 2015, (15): 266-273.

[16]陈其安, 朱 敏, 赖琴云. 基于投资者情绪的投资组合模型研究[J].中国管理科学, 2012,(3): 47-56.

[17]谢 军, 杨春鹏, 闫 伟. 含有无风险资产的情绪最优投资组合[J].系统管理学报, 2012, (4): 540-545.

[18]谢 军, 杨春鹏.风险分散不足与投资者情绪——基于情绪认知的行为投资组合研究[J].软科学, 2012, (8): 131-135.

[19]郭多祚, 佟孟华. 数理金融——资产定价的原理与模型(第2版) [M].北京：清华大学出版社, 2012.61-63.

(编辑：周亮；校对：余华)

Study on Mean-variance Portfolio Selection Based on Investor Sentiment

LUO Yan1,2LIU Xiao-xing2

( 1．DepartmentofFinancialandMathematics,NanjingUniversityofAudit,NanjingJiangsu211815；2．SchoolofEconomicandManagement,SouthEastUniversity,NanjingJiangsu211189)

In this paper,investor sentiment is introduced to the study of portfolio selection. We build a model of sentiment-adjusted portfolio of mean-variance. The optimal invest strategies and the efficient frontier are obtained by Lagrange multiplier method. The results show that the minimum sentiment-adjusted variance decrease with the investor sentiment before the attaining the minimum and then increase with the investor sentiment, which indicates a U-shape relationship. The efficient frontier is consistent with the classic model, but moves up right as the investor sentiment increase. Moreover, we also gain the sentiment-adjusted two fund separation theorem.

investor sentiment;mean-variance; portfolio; efficient frontier

2016-07-03

国家自然科学基金资助项目“资产价格波动与实体经济：影响机制及其动态均衡研究”(项目编号：71473036)、江苏高校哲学社会科学项目“流动性风险与中小企业投融资、定价及风险管理研究”(项目编号：2014SJB97)、江苏省金融工程重点实验室课题“流动性风险与公司动态投资决策研究”(项目编号：NSK2015-11)、中国博士后科学基金项目“连续时间公司最优投资决策研究”(项目编号：2013M541576)

罗 琰(1979- )，男，湖南郴州人，南京审计大学金融数学系副教授，博士，研究方向：金融数学；刘晓星( 1970- ) ，男，湖南隆回人，东南大学经济与管理学院教授，博士生导师，研究方向：金融理论与风险管理

10.16546/j.cnki.cn43-1510/f.2016.05.002

F224；F830.59

A

2095-1361(2016)05-0014-07