Cicada（Tibicen linnei）steers by force vectoring

Samane Zeyghami，Nidhin Babu，Haibo Dong∗

Department of Mechanical and Aerospace Engineering，University of Virginia，Charlottesville，VA，22904，United States

Cicada（Tibicen linnei）steers by force vectoring

Samane Zeyghami，Nidhin Babu，Haibo Dong∗

Department of Mechanical and Aerospace Engineering，University of Virginia，Charlottesville，VA，22904，United States

H i G H L i G H T s

•Several free flights of cicada（Tibicen linnei）are studied（total of 42 wingbeats）.

•Coordination between the aerodynamic force generation and change in flight path is investigated.

•Measurements and calculations show that the aerodynamic force is fixed to the body frame.

•Findings reveal that a simple force vectoring technique is used for steering all these flights.

•A similar strategy can be applied to the design of Micro Air Vehicles.

A R T i C L Ei N F O

Article history:

Accepted 25 December 2015

Available online 4 February 2016

Cicada

Free flight

Force vectoring

Aerial maneuver

Force control

To change flight direction，flying animals modulate aerodynamic force either relative to their bodies to generate torque about the center of mass，or relative to the flight path to produce centripetal force that curvesthetrajectory.Inemployingthelatter，thedirectionofaerodynamicforceremainsfixedinthebody frame and rotations of the body redirect the force.While both aforementioned techniques are essential for flight，it is critical to investigate how an animal balances the two to achieve aerial locomotion.Here，we measured wing and body kinematics of cicada（Tibicen linnei）in free flight，including flight periods of both little and substantial body reorientations.It is found that cicadas employ a common force vectoring techniquetoexecutealltheseflights.Weshowthatthedirectionofthehalf-strokeaveragedaerodynamic force relative to the body is independent of the body orientation，varying in a range of merely 20 deg. Despite directional limitation of the aerodynamic force，pitch and roll torque are generated by altering wing angle of attack and its mean position relative to the center of mass.This results in body rotations which redirect the wing force in the global frame and consequently change the flight trajectory.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

Thecapacitytochangetheflighttrajectoryisessentialforaerial locomotion and survival of flying animals.To adjust the flight course，flying animals modulate the magnitude and orientation of aerodynamic force by altering their wing kinematics.Highly maneuverable insects such as dragonflies［1，2］，damselflies［3］and fruit flies［4］are capable of adjusting the wing stroke plane angle as well as the orientation of the wing in this plane to achieve exceptional control over the aerodynamic force.The ability to change the force direction relative to the body allows these insects to generate aerodynamic torque about the center of mass for body reorientation.While this enhances the maneuverability of a flying animal，it imposes complexity to the wing biomechanics as well as the control system of the flight［5］.Alternatively，measurements have shown that during banked turns flying insects and birds change the flight trajectory while maintaining the direction of aerodynamic force relative to their bodies.In these maneuvers，animals rely on whole-body rotations to redirect the force in the global frame.This strategy is referred to as force vectoring［5］and wasobservedinbankedturnsofinsects［6］，bats［7］andbirds［5，8］. It was argued that force vectoring allows minimal modulations of the wing motion relative to the body［5］.While this is beneficial forsimplifyingthewingbiomechanics，somedegreeofcontrolover theaerodynamic forcedirection relativetothebody isessential for stability and maneuverability［9］.

Understanding the coordination between the aerodynamic force production and the flight reorientation is fundamental to comprehending the aerial locomotion of the insects and birds. Previous measurements and investigations mostly focused on a single flight mode and therefore their conclusions cannot be generalizedtootherflightswithoutfurtherinvestigations.Herewe asked to what extend a flying animal alters the force orientation relativetoitsbodyinordertosteer.Topursuethisgoal，westudied a variety of flights of cicada（Tibicen linnei），including periods of little as well as substantial body reorientations，to examine theextent to which the aerodynamic force is modulated for achieving this range of flights.

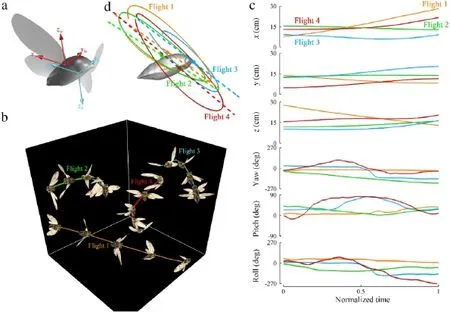
Fig.1.（a）Wing and body coordinate systems of cicada.（b）A selected sequence of images from the reconstructed wing and body motion of different flights.（c）Body kinematics of the cicada in different flights.（d）A sample wing tip trajectory of each flight.The dashed straight line shows the average stroke plane.

Several cicadas（Tibicen linnei）were captured in Dayton，Ohio. A network of marker points were drawn on the wings which were later used to track the motion of the wings.Natural features of the body such the eyes were used to track the body motion. The recording area is equipped with three orthogonally placed Photron Fastcam SA3 60k high speed cameras synchronized to record at 1000 frames per second.After recording several flights of each individual，the wing and body length（（35±2）mm and（30±1）mm for wing and body，respectively）as well as the body mass（（1050±100）mg）were measured.All statistical results are presented as（mean±standard deviation（SD））.A manual 3D surface reconstruction technique was applied to the output from the cameras［10］.The motion of the wings and the body were tracked at each frame（every millisecond）using all three orthogonal images.The reconstructed 3D surfaces of the wings and the body were then meshed using triangular grids［11］.The location of mesh nodes were used to define the wing and the body kinematics.Kinematics of the body can be easily extracted by identifying the location of three points on the body that define a surface（not along a single line）.We used the tail，head and the top-thorax points.To obtain rigid wing kinematics，the root mean squared plane of the wing was defined based on the position of the marker points on the wing at each frame.Since the fore and hind wing move together during flight，they were treated as one wing platform.The orientation of the rigid wing relative to the body was thenexpressedbythreeEulerangles；flapping，deviationandpitch. Theflappinganglerepresentstheforward-backwardmotionofthe wing.Deviation is up and downs motion of the wing with respect to its joint and pitch is the wing rotation about its hinge axis to the body（Fig.1a）.

Over 50 free flights of cicada were recorded during summers of 2011 and 2012.Different flight modes including forward flight，vertical takeoff，banked turn and Immelmann turns were captured among these flights.While the majority of these flights involve significant change in flight heading，we never observed a yaw turn as was reported in other insects and birds such as fruit flies［12］，dragonflies［1］，damselflies［3］and hummingbird［13］.The flight heading change was executed via banked turns or Immelmann turns.To advance with our investigation on understanding the aerodynamics and flight mechanics of cicada free flight，we selected four representative flights composing total of 42 full wingbeats.A selected sequence of images of all these flights are shown in Fig.1b with the quantitative measurements of the body displacement and orientation being presented in Fig.1c.Flight 1，consists of two phases of moving on a straight line with a small body pitch angle and an average forward velocity of 1.88 m·s-1followed by a pitch up and deceleration of the forward velocity. Flight 2 is a banked-turn during which the flight heading changed by 150 deg.The body rolled to the left within the first two flapping stokes，reaching a 90 deg bank angle.The bank angle is very extreme compared to what was observed in turn flights of other insectssuchasfruitflies［4］andblowflies［14］.Themaximumbody roll velocity approached 4000 deg·s-1in this phase.The turn is followed by a slow roll back and flying forward while maintaining the body orientation.Flight 3 resembles an Immelmann（or rolloff-the-top）turnwhichconsistsofanascendinghalf-loopfollowed by a fast roll.After takeoff and a short phase of forward flight，the cicada pitched up in a vertical loop，with mean radius of 0.9 body length，until it attained an upside down orientation with respect to the ground.The maximum pitch velocity exceeded 3000 deg·s-1and was reached at the early stages of pitching up phase.Subsequently，the cicada rolled to reposition the body in straight flight orientation.In flight 4，the cicada body pitched up from 0 to 90 deg within two wingbeats and continued to ascend while maintaining its orientation（body axis normal to the ground）for the next five wingbeats.The vertical velocity of the center of mass was 0.36 m·s-1during this phase.The initial phase was followed by a fast spinning which altered the body’s bank angle more than 180 deg.Rotations faster than 700 deg·s-1occurred about an axis which lies in the body’s frontal plane with the angle between rotation axis and the body normal being（92±22）deg.Several performance parameters of these flights are summarized in Table 1.

Table 1 Performance parameters of different cicada flights.BL and WB stand for body length and wing beat，respectively.

Fig.2.（a）Validation of the quasi-steady model with high fidelity simulations of cicada in forward flight［15］.The orientations of FDS（b）and FUS（c）with respect to the normal to the body are colored differently for each flight.The angle between the force vector and the normal to the body is measured clockwise and the length of the arrow represents the magnitude of the normalized force.The clustering of the arrows in downstroke and upstroke shows that the orientation of the aerodynamic force relative to the body is independent of the body orientation.（d）The orientation of the aerodynamic force relative to the body normal vector is limited to the surface of a cone with the axis of the cone coinciding with the body normal and the angle of the cone of 17 and 135 deg for downstroke（green cone）and upstroke（blue cone），respectively.（For interpretation of the references to colour in this figure legend，the reader is referred to the web version of this article.）

Despite the large body reorientation，the motion of the wings relative to the body was stereotypical among all the flights，with small flapping amplitude and fast rotations at the stroke reversal. The wing tip trajectories were oval shaped with the ratio of the minor to major axis lengths being 0.28±0.09（Fig.1d）.The wing stroke plane angle is inclined with respect to the body with wings moving forward and downward in downstroke and backward and upward in upstroke.Despite the substantial changes in the body orientation，the variations in the stroke plane angle with respect to the body were small which implies these insects have little control over this angle.The average stroke planes angles with respect to the body remains relatively invariant；（47±12）deg（n=84）.Besides slight variations in the wing stroke plane angle，theflappingamplitudeofthewinginthestrokeplaneaswellasthe mean flapping angle（the average location of the wing with respect to the center of mass）was modulated from one stroke to another. Flapping frequency varied slightly among the individuals as well as during the maneuver；（50.5±8.8）Hz（n=42）.In addition，cicadas were able to adjust the ratio of the downstroke to upstroke duration between 0.6 and 1.4.Orientation of the wing surface with respect to the stroke plane was adjusted via modulating the wing pitch angle.The pitch angle of the wing is shallow in downstrokes but varies largely；（-7.1± 11.5）deg，whereas it is higher in upstrokes；（31.6±20.1）deg.

To probe the dynamics of these flight，we calculated the aerodynamic force generated by the wings，using a quasi-steady model［16，17］.The accuracy of the method was examined by comparing our prediction with the aerodynamic lift calculated fromhighfidelityCFDsimulationsofacicadainforwardflight［15］，shown in Fig.2a.Aerodynamic force was generated in both downstroke and upstroke.When flying forward（i.e.flight 1），the downstroke force carries out the entire weight supporting role whileupstrokeforceprovidesthepropulsion.Yet，theseroleswere found to be interchangeable when body reorients during the aerial maneuvers.For instance in both turning flights reported in this work，thedownstrokeforceprovidedthecentrifugalforcerequired for bending the flight path while the weight supporting role was mostlycarriedoutbyupstrokeforceduetotherotationofthewing strokeplanemovingwiththebody（Fig.3a）.Tofurthervalidateour theory，weestimatedtheaveragecentripetalaccelerationinflights 2-4 using the average travel velocity and the radius of turn.The calculated values were below 9.2 m·s-2（＜g）for all these flights，guaranteeing that the lift force is able to provide this acceleration.

To quantify the variation of the aerodynamic force direction during flight，we calculated the angle between the averagedaerodynamic force in downstroke，FDS，and upstroke，FUS，and the normal vector to the body for all 42 wingbeats.All forces were normalized by the body weight.The results are plotted in Fig.2b andc.Visualinspectionofthisfigureillustratesthattheorientation of the aerodynamic force in both downstroke and upstroke is restricted relative to the body，regardless of the body orientation. In particular，FDSmaintains a uniform orientation with respect to the body’s normal vector，with the angle between the two vectors being（17±7）deg.The angle between FUSand the body normal is（135±10）deg.These results show that cicada can only change the direction of the aerodynamic force vector in a restricted range in its body frame.In fact，the orientation of the aerodynamic force relative to the body normal is restricted to the surface of a cone with its axis coinciding with the body normal（Fig.2d）.While a similar phenomenon was observed in banked turn of smaller insectssuchasfruitflies［4，6，18］，houseflies［19］andblowflies［20］，our results for the first time show that a wide range of flight modes can be achieved by force vectoring.This technique eliminates the need for altering the orientation of the force relative to the body and thus simplifies the design of the wing joint biomechanics.

Fig.3.（a）The orientation of the average aerodynamic force（FDSand FUS），body normal vector（n）and the cicada body are shown within a consecutive downstroke and upstroke of flight 3.The flight path is shown with dashed lines and inside the curvature of the flight path is shaded.It is evident that due to the body orientation in the global frame，the downstroke force is relatively normal to the flight path，providing the centripetal force for curving the trajectory.On the other hand，the upstroke force has a large upward component that resists gravitational force.（b）Pitch-torque-producing wing tip trajectories of flight 4 are colored by the stroke averaged pitch torque generated by the wing.The cicada shifts the wing’s average position（shown by a closed circle with the same color as the tip trajectory）relative to the center of mass（black and white circle）to generate pitch torque.（For interpretation of the references to colour in this figure legend，the reader is referred to the web version of this article.）

To change the movement trajectory，the orientation of the force relative to the flight path has to change.To investigate the mechanism by which cicadas redirect the force in the global frame，we examined the relative orientation of the rotation axis（for rotations faster than 700 deg·s-1）and the half-stroke-averaged force.Body rotations that occur about the force vector preserve the orientation of the force in the global frame and do not result in flight trajectory changes.On the contrary，rotations about an axis that deviates from aerodynamic force，redirects the force and thus alters the flight trajectory.Our results show that body rotations occur about an axis which predominantly redirects the aerodynamic force；the angles between the rotation axis and FDSand FUSwere（75±12）deg and（56±21）deg，respectively.

Despite the directional limitation of the aerodynamic force in the body frame，cicadas can generate rotations about the body roll and pitch axes.Roll torque was produced by asymmetrically varying the angle of attack of the bilateral wings.The magnitude of the roll torque was strongly correlated with the wing angle of attack（R2=0.6，n=84）.Pitch torque was exerted by shifting the mean position of the wing to offset the force relative to the center of mass（Fig.3b），similar to the technique employed by fruit flies［21］.Themagnitudeofthepitchtorquewasdirectlycorrelated with the average wing deviation angle（R2=0.63）.Since，the downstroke force is normal to the cicada body，no significant yaw torque can be generated during this half of the flapping cycle. However，in upstroke，asymmetric bilateral wing kinematics can result in yaw torque generation.Our measurements show that the magnitude of the yaw velocity is smaller than that of pitch or roll velocity and oscillates within wingbeats，increasing in upstroke and decreasing in downstroke.

We conclude that all the free flights studied here are governed by a unified force control strategy，despite the fact that they share little in common with regard to the body orientation and motion.Therestrictedvariationsintheorientationoftheaerodynamic forcerelativetothebodynecessitatesthebodytoreorientforredirecting the force and changing the flight path.Directional limitation of the aerodynamic force in the body frame also simplifies the mechanicsofthewinghinge，asitreducestheneedforimplementing complex alternations in the wing motion.The importance of these results is twofold；they clarify the aerodynamics and mechanics of cicada free flight，and they prove that force vectoring can be successfully implemented for designing large payload and yet maneuverable flapping wing micro air vehicles（MAVs）.

Acknowledgments

This research is funded by the National Natural Science Foundation of China（1313217）and Air Force Office of Scientific Research（FA9550-12-1-007）monitored by Dr.Douglas Smith.

［1］D.E.Alexander，Wind tunnel studies of turns by flying dragonflies，J.Exp.Biol. 122（1986）81-98.

［2］C.Koehler，T.Wischgou，H.Dong，et al.，Vortex visualization in ultra low reynolds number insect flight，IEEE Trans.Vis.Comput.Graphics 17（2011）2071-2079.

［3］S.Zeyghami，H.Dong，Coupling of the wings and the body dynamics enhances damselfly maneuverability，2015 arXiv:1502.06835，arXiv preprint.

［4］S.N.Fry，R.Sayaman，M.H.Dickinson，The aerodynamics of free-flight maneuvers in drosophila，Science 300（2003）495-498.

［5］I.G.Ros，L.C.Bassman，M.A.Badger，et al.，Pigeons steer like helicopters and generate down-and upstroke lift during low speed turns，Proc.Natl.Acad.Sci. 108（2011）19990-19995.

［6］F.T.Muijres，M.J.Elzinga，J.M.Melis，et al.，Flies evade looming targets by executing rapid visually directed banked turns，Science 344（2014）172-177.

［7］J.Iriarte-Díaz，S.M.Swartz，Kinematics of slow turn maneuvering in the fruit bat cynopterus brachyotis，J.Exp.Biol.211（2008）3478-3489.

［8］T.Hedrick，A.Biewener，Low speed maneuvering flight of the rose-breasted cockatoo（Eolophus roseicapillus）.I.Kinematic and neuromuscular control of turning，J.Exp.Biol.210（2007）1897-1911.

［9］K.Y.Ma，P.Chirarattananon，S.B.Fuller，et al.，Controlled flight of a biologically inspired，insect-scale robot，Science 340（2013）603-607.

［10］C.Koehler，Z.X.Liang，Z.Gaston，et al.，3D reconstruction and analysis of wing deformation in free-flying dragonflies，J.Exp.Biol.215（2012）3018-3027.

［11］G.Liu，Y.Ren，J.Z.Zhu，et al.，Thrust producing mechanisms in ray-inspired underwater vehicle propulsion，Theor.Appl.Mech.Lett.5（2015）54-57.

［12］A.J.Bergou，L.Ristroph，J.Guckenheimer，et al.，Fruit flies modulate passive wing pitching to generate in-flight turns，Phys.Rev.Lett.104（2010）148101.

［13］T.L.Hedrick，B.Cheng，X.Deng，Wingbeat time and the scaling of passive rotational damping in flapping flight，Science 324（2009）252-255.

［14］C.Schilstra，J.H.Hateren，Blowfly flight and optic flow.I.Thorax kinematics and flight dynamics，J.Exp.Biol.202（1999）1481-1490.

［15］H.Wan，H.Dong，K.Gai，Computational investigation of cicada aerodynamics in forward flight，J.R.Soc.Interface 12（2015）20141116.

［16］G.J.Berman，Z.J.Wang，Energy-minimizing kinematics in hovering insect flight，J.Fluid Mech.582（2007）153-168.

［17］M.Ghommem，D.Garcia，V.M.Calo，Enclosure enhancement of flight performance，Theor.Appl.Mech.Lett.4（2014）062003.

［18］K.G.Götz，C.Wehrhahn，Optomotor control of the force of flight in drosophila and musca，Biol.Cybernet.51（1984）129-134.

［19］H.Wagner，Flight performance and visual control of flight of the free-flying housefly（MuscadomesticaL.）I.Organizationoftheflightmotor，Philos.Trans. R.Soc.B 312（1986）527-551.

［20］C.Schilstra，J.Hateren，Blowfly flight and optic flow.I.Thorax kinematics and flight dynamics，J.Exp.Biol.202（1999）1481-1490.

［21］J.Zanker，On the mechanism of speed and altitude control in drosophila melanogaster，Physiol.Entomol.13（1988）351-361.

17 November 2015

.

E-mail address:haibo.dong@virginia.edu（H.Dong）.

http://dx.doi.org/10.1016/j.taml.2015.12.006

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Biomechanics and Interdiscipline