Stability analysis of liquid filled spacecraft system with flexible attachment by using the energy-Casimir method

Yulong Yan，Baozeng Yue

School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China

Stability analysis of liquid filled spacecraft system with flexible attachment by using the energy-Casimir method

Yulong Yan，Baozeng Yue∗

School of Aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China

H i G H L i G H T s

•The mechanical model of the coupled spacecraft system is constructed.

•The nonlinear stability conditions are obtained by using the energy-Casimir method.

•The stability region of the coupled system is obtained in the parameter space.

A R T i C L Ei N F O

Article history:

3 March 2016

Accepted 4 March 2016

Available online 24 March 2016

Energy-Casimir method

Liquid sloshing

Nonlinear stability

Flexible appendage

The stability of partly liquid filled spacecraft with flexible attachment was investigated in this paper. Liquidsloshingdynamics wassimplifiedas thespring-massmodel，and flexibleattachmentwasmodeled as the linear shearing beam.The dynamic equations and Hamiltonian of the coupled spacecraft system were given by analyzing the rigid body，liquid fuel，and flexible appendage.Nonlinear stability conditions of the coupled spacecraft system were derived by computing the variation of Casimir function which was added to the Hamiltonian.The stable region of the parameter space was given and validated by numerical computation.Related results suggest that the change of inertia matrix，the length of flexible attachment，spacecraft spinning rate，and filled ratio of liquid fuel tank have strong influence on the stability of the spacecraft system.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

The rapid development of aerospace industry requires modern spacecrafttocarrylargeamountsofliquidfuel，andthesizeofflexible attachments such as the solar panel，antennae，manipulator，is much bigger than before.The motion of the rigid body，liquid fuel，and flexible attachments constituted the complex dynamic system of spacecraft.Take the Cassini-Huygens as an example，which is an unmanned spacecraft sent to the planet Saturn［1］.The spacecraftatlaunchweighed5712kg，whichincluded3132kgofpropellants.The flexible appendages of the spacecraft contained an 11-meter boom which was used to mount the magnetometer instrument and three other 10-meter rod-like booms which acted as the antennas for the radio plasma wave subsystem.The influence of liquid fuel and flexible attachments should be considered in modeling and analyzing of spacecraft dynamic system，while the weak nonlinear analysis based on perturbation theory was not appropriate for this situation.Related researches［2，3］show that complex nonlineardynamicbehaviorssuchasstatic，periodicmotion，quasiperiodic motion and chaos will be shown in the coupled spacecraft system，and the types of stable motion in-plane modes and outplane modes are different when the parameters of the external excitation varied.

Energy-Casimir method can be viewed as a generalization of the classical Lagrange-Dirichlet method and was first proposed by Arnold［4］in studying the stability of stationary flows of perfect liquid.This method was widely used in stability analysis such as the rigid body with flexible appendage［5，6］，liquid and plasmas［7］.Casimir function［8］should be used when the energy-Casimir method was adopted in stability analysis. In this way，the conserved quantity can be captured by the Casimir function.In order to overcome the difficulty of constructing the Casimir function，energy-moment method was used to research the stability problems.Energy-moment method is a simplified method because the energy function and the moment map were employed in stability analysis.Simo［9］showed the stability of relative equilibria by the reduced energy-momentum method，and analyzed the nonlinear stability of three dimensional elasticity［10］，coupled rigid bodies and geometricallyexact rods［11］.This method has been extended into stability analysis of the rigid body with a spring-mass particle in the perfect liquid［12］，underwater vehicle［13，14］，nonholonomic system［15］，and plasmas［16］.

The stability of the rigid body with flexible attachments can be analyzed by using energy-Casimir method.The dynamic equations of the rigid-flexible coupled system were derived by using Hamiltonian and Poisson bracket，and the stability of the coupled dynamic system was analyzed［6］.The detailed derivations of the nonlinear stability of the rigid body with a linear shearing beam，and the stability conditions of the trivial and untrivial solutions were obtained［5］.The rotation and translation motion of the rigid body with a cantilever beam was discussed by Kane［17］，and centrifugal stiffening effect was first proposed.Coupled system which wasconstitutedbyaplanarrigidbodyandflexibleattachmentwas studied by Bloch［18］，and the nonlinear stability of the equilibria of the equations was discussed.There are also some papers about attitude stability of liquid filled spacecraft.Nonlinear stability of asymmetrical rigid body with full liquid filled satellite was researched by using energy-Casimir method［19］，while the self-spinning stability of full liquid filled satellite with flexible appendage was also studied by the same method［20］.The attitude stability of partly liquid filled spacecraft was researched by using energy-Casimir methods，and the liquid sloshing dynamics was simplified as equivalent mass-spring mechanical model［21］and pendulum model［22］to analogue the liquid sloshing dynamics，the stability conditions，and stable region were also given.

In order to meet the precision requirement for modern liquid filled spacecraft with flexible appendages，the impact of rigid-flexible-liquid coupled effect on the spacecraft dynamics and control should be more carefully considered in detail.The equivalent mechanics models and computational fluid dynamics were often used to estimate the dynamic influence of propellant sloshing and attachment vibration on spacecraft［23］.Hybridcoordinate and spring-mass equivalent model［24］，smoothed particle hydrodynamics and absolute nodal coordinate formulation［25］can be utilized to model the spacecraft consisting of a liquid-filled rigid platform and some flexible appendages.There are also some control strategies，such as the variable structure controller［26］，robust input shapers［27］for sloshing suppression of the coupled spacecraft system.The attitude maneuver of liquid-filled spacecraft with a cantilever appendage was studied by Yang［28］and the stability criteria of attitude maneuver were derived，while the sloshing liquid was modeled as a viscous pendulum.Relatedresearchesmentionedabovemainlyfocusedondynamical modeling and control scheme of the rigid-liquid-flexible coupledspacecraftsystem.However，itisfarawaytobecompletely solvedfortherigid-liquid-flexiblecoupleddynamicsproblem.For example，as we known，little attention has been devoted to the analytic solution of the stability of partly liquid filled spacecraft system with flexible attachment which plays an important role in the spacecraft dynamics analysis.Energy-Casimir method is an effective method to deal with the stability problem of spacecraft system，and the general stability conditions of the coupled spacecraft system can be obtained.

This paper is concentrated on the stability of the rigid-liquidflexible coupled spacecraft dynamical system by the energy-Casimir method.The liquid fuel is modeled as a mass-spring mechanical model in order to consider lateral moving in one direction.For linear planar lateral liquid motion，this model is effective to describe linear dynamics of liquid motion and can be used to formulate the dynamic system behavior properly. The flexible attachment is simplified as a linear shearing beam. The framework of this article is this:The mechanical model of the coupled system is given，and dynamic equations and Hamilton function are deduced.Stability conditions were derivedby computing the variation of Casimir and energy function.The spin-rotation stability conditions of the coupled spacecraft system were given and the effectiveness of the theoretical derivation was verified by numerical simulation.Related results suggest that the change of inertia moment of rigid spacecraft，the length of beam，and filled ratio of the tank have strong influence on the stability of the coupled system.Conclusions were presented.

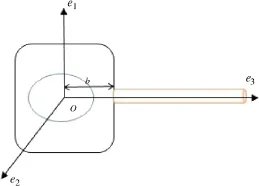
Fig.1.Dynamic model of liquid filled spacecraft with flexible attachment.

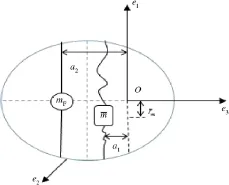
Fig.2.Equivalent mass-spring mechanical model of liquid fuel in spacecraft.

The mechanical model of the spacecraft system with flexible attachment and ellipsoid tank is illustrated in Fig.1.In order to research the attitude stability of the coupled system，the body frame is centered at mass center O of the rigid spacecraft.The reference axes（e1，e2，e3）of the body frame are principal axes of rigid spacecraft and JH=diag（j11，j22，j33）denotes the inertia matrix of rigid spacecraft respect to the body frame.

The equivalent mechanical model which was modeled as the mass-spring mechanical model is shown in Fig.2.Mass of sloshing liquid is represented by¯m，which is attached to the linear spring. The general position of¯m is r¯m=（rm，0，a1）T，while the static position of¯m is r′¯m=（0，0，a1）T.Rest of the fuel mass mFis regarded as stationary，and its position is denoted by rF=（0，0，a2）T.

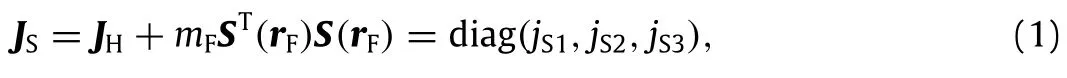
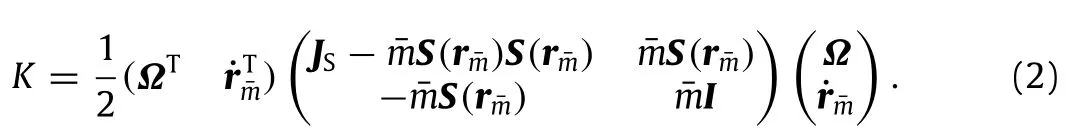
The equivalent elastic force applied to moving mass can be denoted by fint=-k（r¯m-r′¯m）=-∂P/∂（r¯m-r′¯m），and k is the equivalent stiffness of the spring.Thus，the energy function of rigid-liquidcoupledsystemisthesumofkineticenergyandelastic potential energy of the spring.

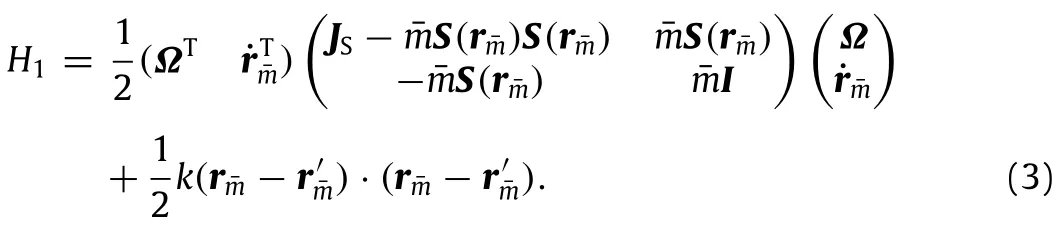
Next，the model of flexible attachment is considered in the subsequentparts.Theflexibleattachmentissimplifiedasthelinear shearing beam，and the beam is along the direction of e3-axis. The connection position between flexible attachment and rigid body can be represented by b=（0，0，b）T.The length of the beam is L and the uniform mass per unit length of the beam isρ0. The convected displacement and momentum density of the beam at point s are expressed as rb（s）andσ（s），respectively.K is the diagonal matrix of elastic coefficients of the shearing beam.The energy function of the beam can be represented by

The boundary conditions of the beam are rb（0）=b=Hamiltonian of the coupled system can be given by Eqs.（3）and（4）.

The total angular momentum of the rigid and liquid parts of the spacecraft system can be defined asΠ =JSΩ- ¯mr¯m×（r¯m×Ω）+ ¯mr¯m×˙r¯m，and the linear momentum of sloshing mass is set as P¯m=-¯mr¯m×Ω+ ¯m˙r¯m.Thus，the dynamic equations of the coupled spacecraft system can be given.

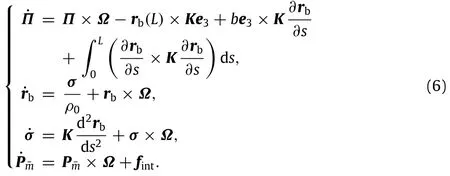
The energy and angular momentum of the coupled spacecraft system will be the conserved quantities if the coupled system without external forces or torques.Nonlinear stability of the coupled system will be researched by computing variations of the sum of Hamiltonian and Casimir function.The total angular momentum of the coupled spacecraft system can be expressed asSuppose thatC=‖α‖2，andCasimirfunctioncanbetakenasψ=ψC（C）/2. The first and second variation of Casimir function can be defined asThe expression of the sum of Hamiltonian and Casimir function is

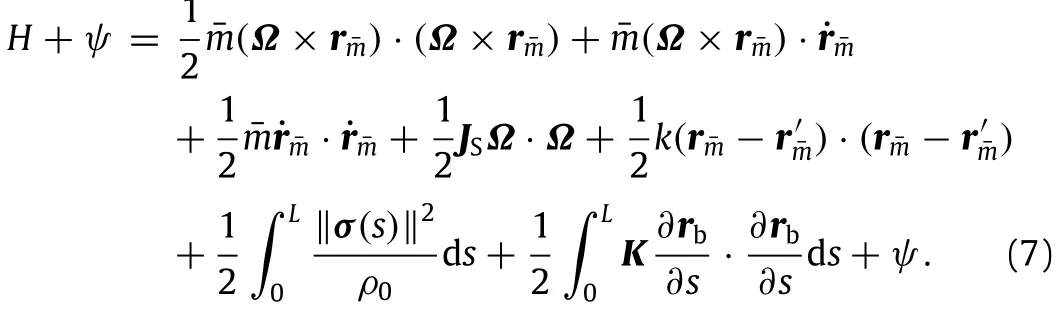
Firstly，the definitions will be given as follows:

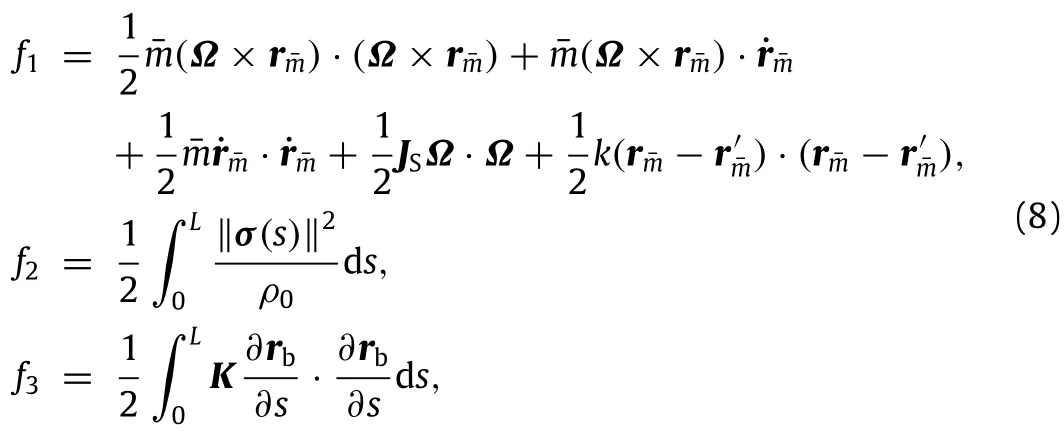
where f1is the energy function of rigid-liquid coupled system，and f2，f3are the kinetic energy and potential energy of the beam，respectively.The first variations of f1，f2，f3can be given by

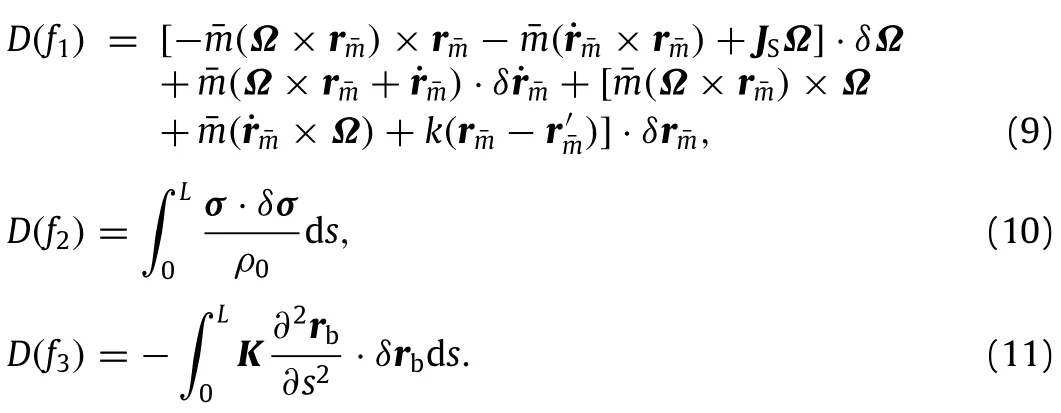
The first variation of Casimir function can be represented by

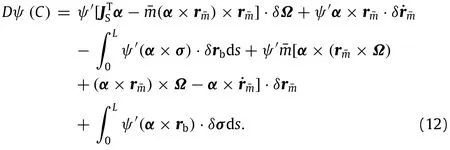
The first variation of H+ψcan be derived from Eqs.（9）-（12）

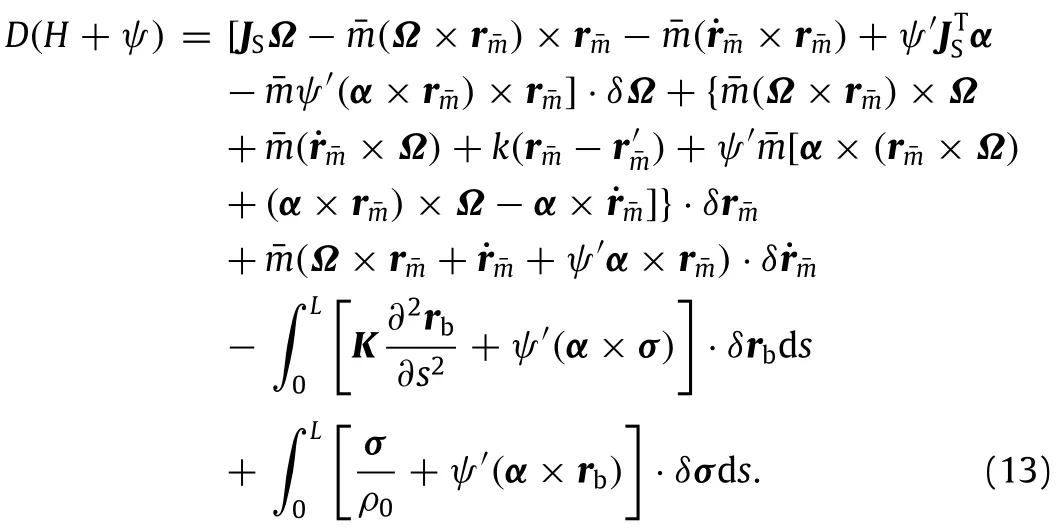
Next，the second variation of H+ψwill be computed.The second variation of f1can be obtained from Eq.（9）.

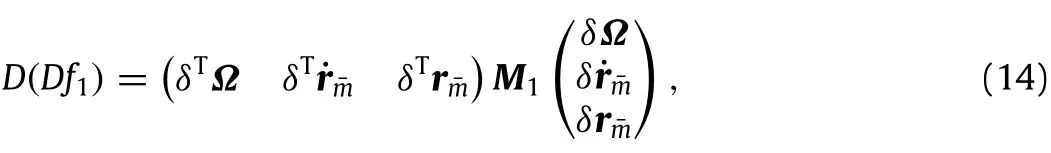
where（see Box I）.

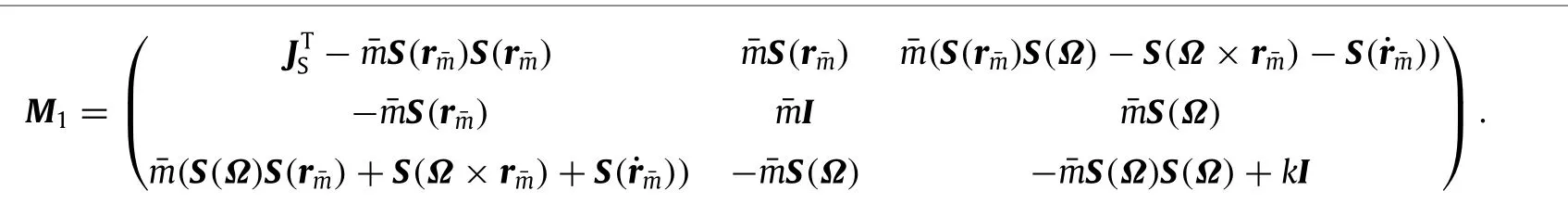
Box I.

Similarly，the second variations of f2，f3can be given from Eqs.（10）and（11）.Suppose K is a diagonal matrix.The estimate of the upper bound can be derived by using Poincare-type inequality.

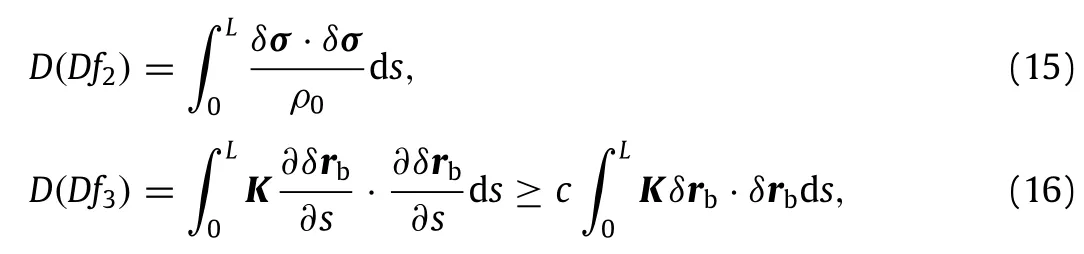
where c=π2/4L2.Then，the second variation of Casimir function can be computed by Eq.（12）.

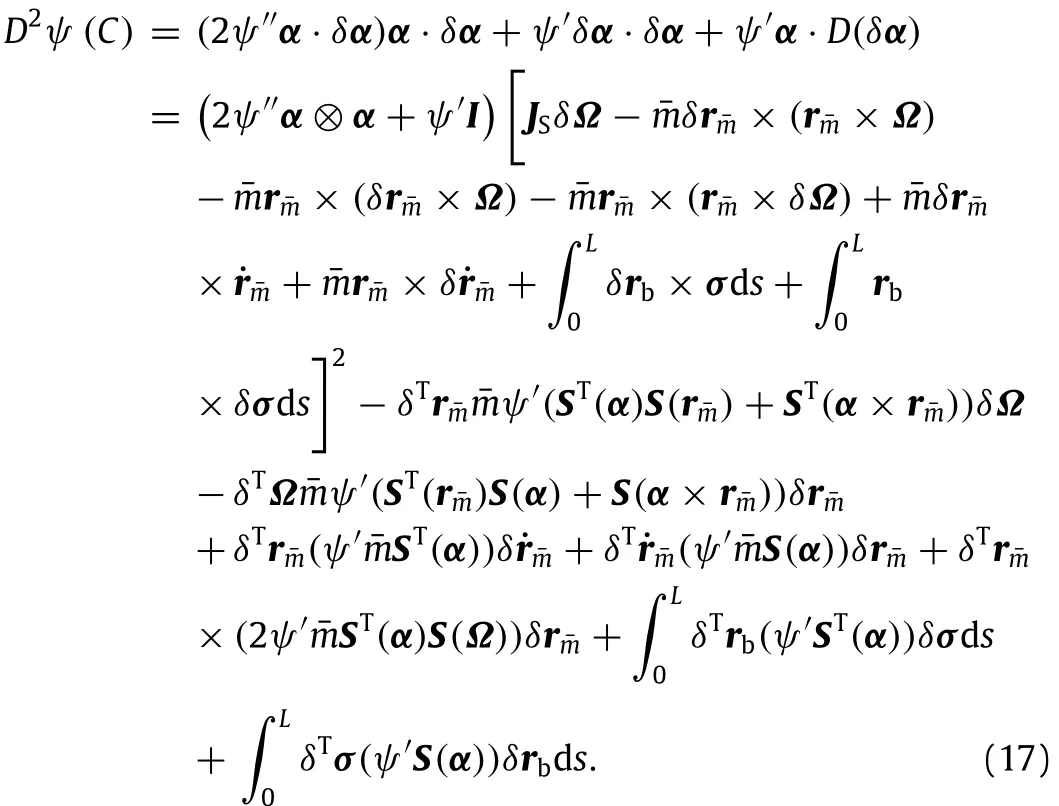
From Eqs.（14）-（17），the second variation of H+ψis

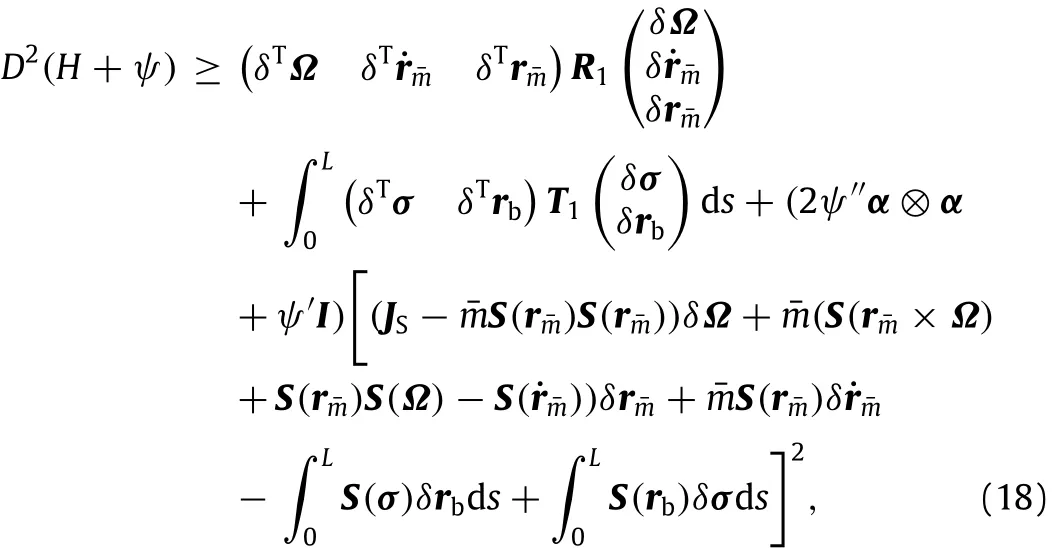
where

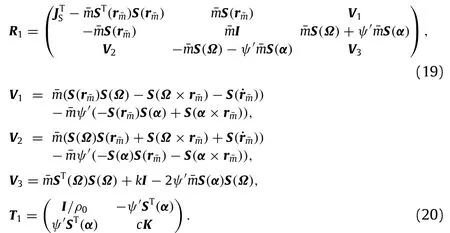
Let P=2ψ′α⊗α+ψ′I，and the last term of Eq.（18）can be expanded as

where

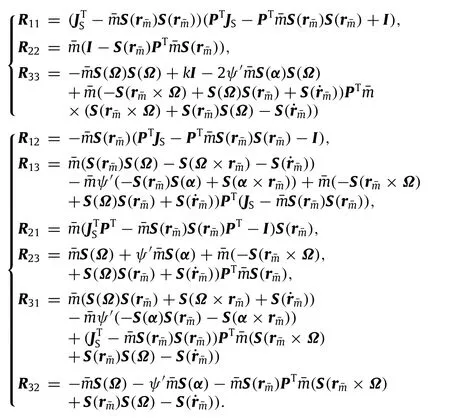
The following expression can be calculated by expanding the last term of Eq.（21）.

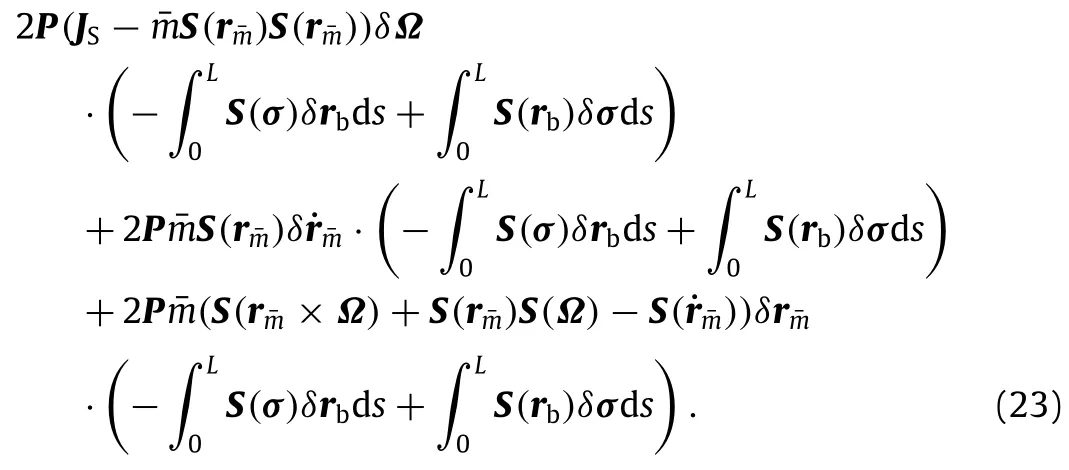
Now the quadratic term ofδΩin Eq.（18）and the first term in Eq.（23）will be collected，then

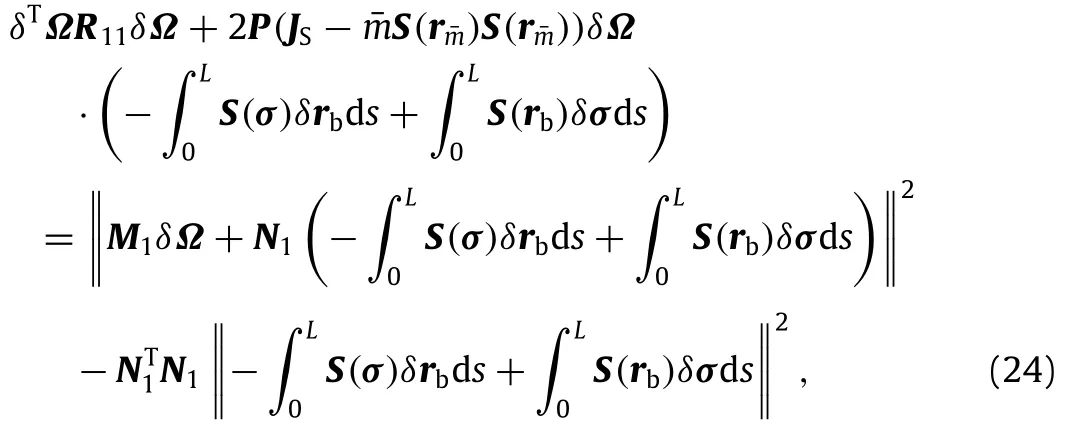
where

Similarly，the second and third terms of Eq.（23）can be analyzed by the following definitions:

Then

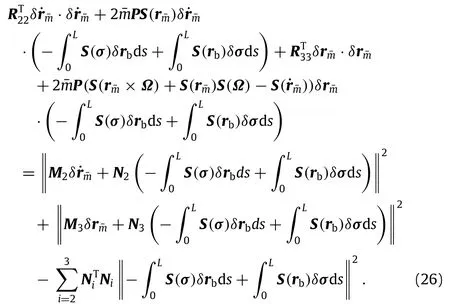
Collect the second term of Eqs.（18）and（24）-（26），then

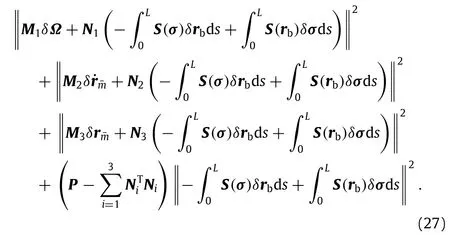
The first three terms of Eq.（27）is positive obviously，and the last term of Eq.（27）will be examined.

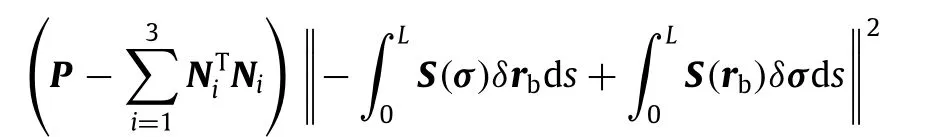
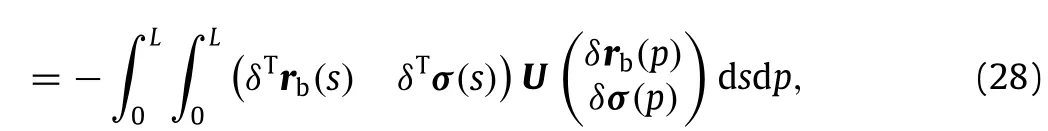
where（see Box II）.

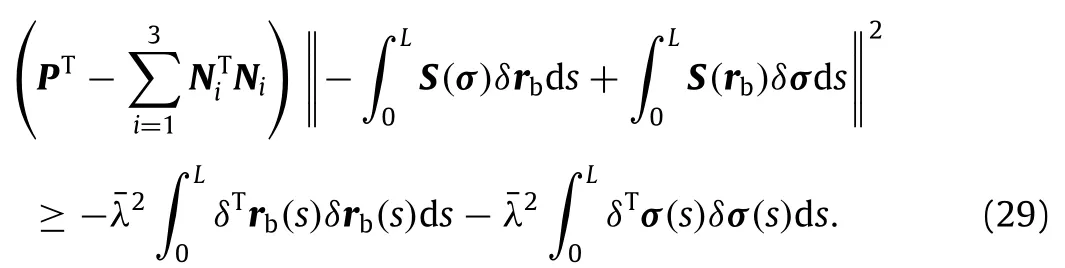
Thus，the expression can be obtained from Eq.（29）.

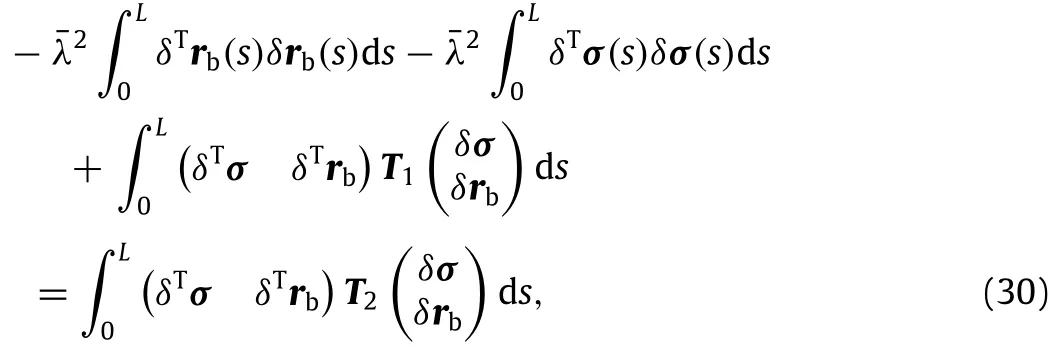
where

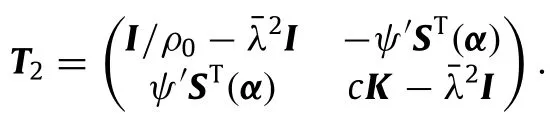
Summarizing above derivations，Eq.（18）can be represented by

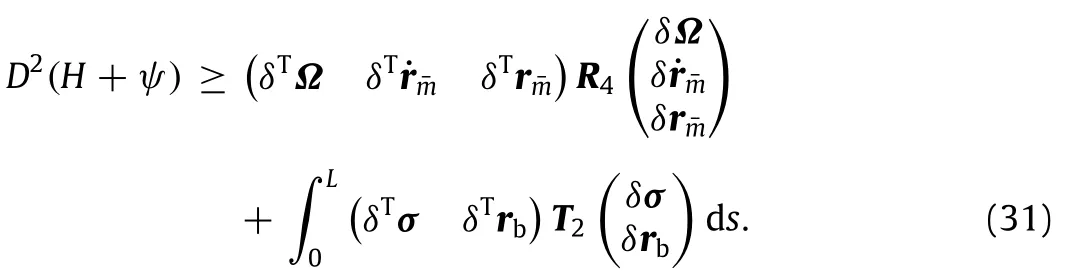
Suppose that Re4，Te2are the matrixes of R4，T2at the equilibrium，respectively.According to Eq.（31），the nonlinear stability theorem of the coupled spacecraft system can be expressed as:if the matrixes Re4，Te2are positive definite，then the coupled spacecraft system is nonlinear stability.

ThestabilityofsolutionofEq.（6）willbediscussed.Agrawal［29］showed that if a steady-state solution exists，it can only be a rotation of the complete spacecraft，rigid body and propellant，like a rigid body，and for a body with flexible elements，the only stable spin axis is the axis of maximum moment of inertia. The equilibrium of the coupled spacecraft system is expressed as（Ωe，˙re¯m，re¯m，σe，reb），and the angular velocity isΩe= ωe3e3.If the beamdoesnotstretch，thenreb（s）=（b+s）e3，σe（s）=0，0≤s≤l. Equilibrium of sloshing mass satisfied that rm=0，˙rm=0，i.e.the position of the sloshing mass¯m is at rest position，and the velocity is zero.The angular momentum at the equilibrium isαe=j33ωe3e3，and the value ofψ′，ψ′at the equilibrium can be represented by

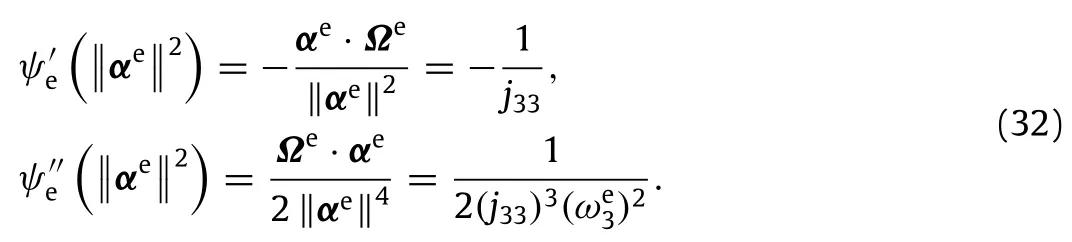
In order to assure that Te2is positive definite，the following inequalities should be satisfied.

Box II.

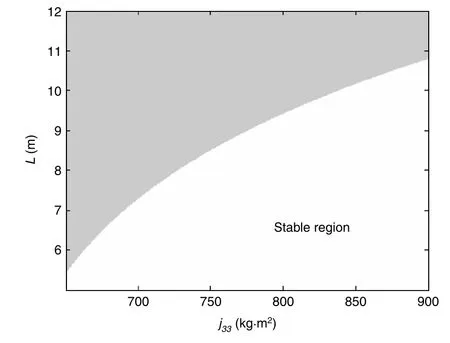
Fig.3.Distribution of stable region in parameter space（j33，L），and the unshaded area represents the stable region.

where

By substituting the equilibrium into the matrix R4，we can get that matrix Re4is the semi-positive.The coupled spacecraft system is nonlinear stability if Eq.（33）are satisfied.Now the physical meaning of these conditions will be explained.The first two inequalities are conditions about the admissible rotation rates of the configuration，i.e.the angular frequency of the system should not exceed the modified characteristic transverse beam frequencies.The last two conditions are similar to the classical stable conditions on the stable axes of rotation for the rigid body，and the inertia should be modified due to liquid fuel and flexible attachments.If liquid fuel is ignored，the stability conditions will be consistent with related conclusions［5］.

The computational results will be given in the following parts. The corresponding parameters are given in Table 1.The unshaded area in Fig.3 represents the stable region in the parameter space（j33，L）.It is illustrated in Fig.3 that the increase of the inertia of spacecraft will strengthen the stability of the coupled spacecraft system，while the increase of the length of the beam will weaken the stability of the coupled system.

The effect of angular velocity to stability of the coupled spacecraft system was given in Fig.4，and the unshaded area in Fig.4 denotes the stable region.It is shown in Fig.4 that the increaseofangularvelocitywillweakenthestabilityofthecoupled system.

The effect of the filled ratio of tank will be considered.The corresponding parameters are also given in Table 1.Suppose the maximum mass of the liquid fuel in the tank is mliquid=300 kg，and the mass of total liquid denotes as mtotal=mslosh+mrest，wheremslosh，mrestrepresentthemassofsloshingfuelandrestfuel，respectively.Setη=mtotal/mliquidas filled ratio of the fuel tank，and 0≤η≤1.According to the conclusions of sloshing liquid in the spherical tank by Bauer［30］and Dodge［31］，the parameters of mslosh/mtotal，mrest/mtotal，a1，a2，and sloshing frequency as the filled ratio of the fuel tank varied can be given.

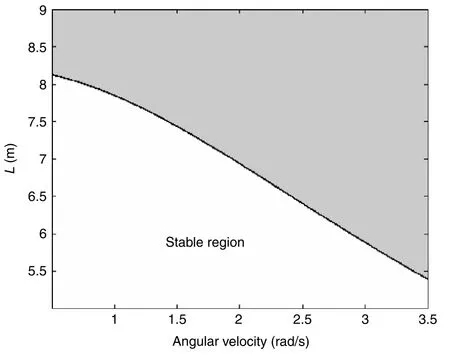
Fig.4.Distribution of stable region in parameter space（ωe3，L），and the unshaded area represents the stable region.

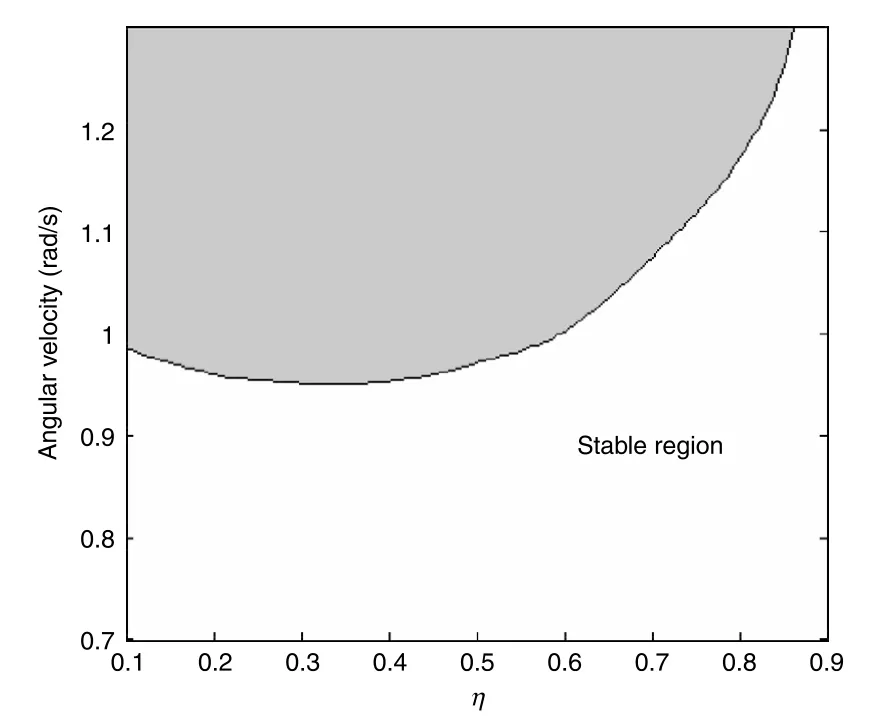
Fig.5.Distribution of stable region asηvaried，and the unshaded area represents the stable region.

The stable region is shown as unshaded area in Fig.5，while the parameters of rigid spacecraft and flexible attachment are fixed. Stability of the coupled system will be weakened asηless than 0.3. This is related to the rapid increase of mslosh，and mslosh＞ mrest. The increase rate of mslosh，and mrestwill be almost same as 0.3≤η≤ 0.4，and the boundary of the stable and unstable region has no significant change in parameterη.The increase rate of mrestis rapid than mslosh，as 0.4≤η≤0.62，and the stability of the coupled spacecraft system will be gradually increased.The mass of rest liquid will be larger than that of the sloshing liquid when ηis bigger than 0.62，and the corresponding stable region will be growing rapidly.The results demonstrate that the increase ofmslosh，will reduce the stability of liquid-filled spacecraft，while the increaseofmrestwillstrengthenthestabilityofthecoupledsystem. This result is in agreement with the conclusions by Yue［21］（2013）that increase of mslosh，will decrease the stability of liquid filled spacecraft.

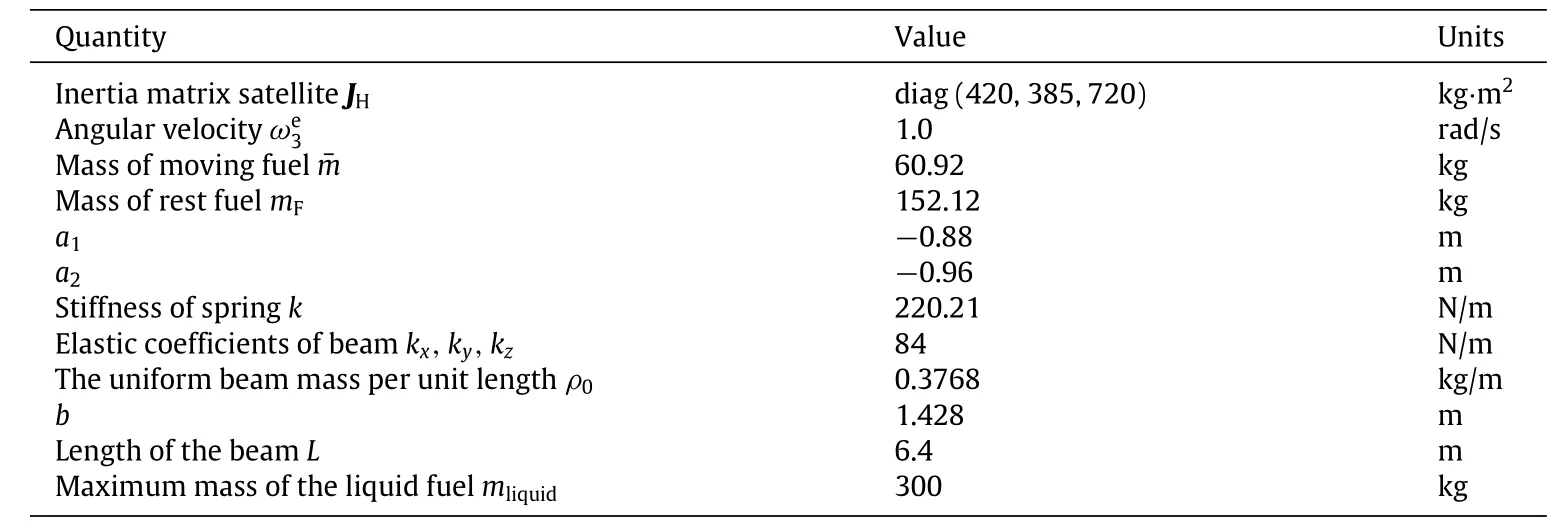
Table 1 Physical parameters for rigid-liquid-flexible coupled spacecraft system.

This paper mainly concerns about the stability of the liquid filled spacecraft with flexible attachment.First，the model of the rigid-liquid-flexible coupled system was built，the total energy function and Casimir function were constructed by analyzing the Hamiltonian of each subsystem.Then，the equilibrium conditions for the coupled spacecraft system were obtained and nonlinear stability conditions were captured by using the energy-Casimir method.Finally，the numerical computations were conducted to verify the validity of the result presented.The computational results shown that the increase of inertia matrix will strengthen the stability of coupled system，and the increase of the length of beam and the spacecraft spinning rate will weaken the stability of coupled system，while the change of the filled ratio of liquid fuel tankhavecomplexinfluenceonthestabilityofcoupledliquidfilled flexible spacecraft system.

Acknowledgments

This work was supported by the National Natural Science Foundation of China（11472041，11532002），the Innovation Fund DesignatedforGraduateStudentsofBeijingInstituteofTechnology（2015CX10003），and the Research Fund for the Doctoral Program of Higher Education of China（20131101110002）.

［1］D.L.Matson，L.J.Spilker，J.Lebreton，The Cassini/Huygens mission to the Saturnian system，Space Sci.Rev.104（2002）1-58. http://dx.doi.org/10.1023/A:1023609211620.

［2］B.Z.Yue，Nonlinear coupled dynamics of liquid-filled spherical container in microgravity，Appl.Math.Mech.Engl.29（2008）1085-1092. http://dx.doi.org/10.1007/s10483-008-0812-y.

［3］M.Utsumi，A mechanical model for low-gravity sloshing in an axisymmetric tank，Trans.ASME，J.Appl.Mech.71（2004）724-730. http://dx.doi.org/10.1115/1.1794700.

［4］V.I.Arnold，An a priori estimate in the theory of hydrodynamic stability，Izv. Vyssh.Uchebn.Zaved.Mat.5（1966）3-5.

［5］T.A.Posbergh，P.S.Krishnaprasad，J.E.Marsden，Stability analysis of a rigid body with a flexible attachment using the energy-Casimir method，Commun. Contemp.Math.68（1987）253-273.

［6］P.S.Krishnaprasad，J.E.Marsden，Hamiltonian structures and stability for rigid bodies with flexible attachments，Arch.Ration.Mech.Anal.98（1987）71-93.

［7］D.D.Holm，J.E.Marsden，T.Ratiu，et al.，Nonlinear stability of fluid and plasma equilibria，Phys.Rep.115（1991）15-59. http://dx.doi.org/10.1007/BF01881678.

［8］A.M.Bloch，J.Baillieul，P.Crouch，et al.，Nonholonomic Mechanics and Control，Springer，New York，2003.

［9］J.C.Simo，D.Lewis，J.E.Marsden，Stability of relative equilibria.Part I:The reduced energy-momentum method，Arch.Ration.Mech.Anal.115（1991）15-59.http://dx.doi.org/10.1007/BF01881678.

［10］J.C.Simo，T.A.Posbergh，J.E.Marsden，Stability of relative equilibria II: Three dimensional elasticity，Arch.Ration.Mech.Anal.115（1991）61-100. http://dx.doi.org/10.1007/BF01881679.

［11］J.C.Simo，T.A.Posbergh，J.E.Marsden，Stability of coupled rigid body and geometrically exact rods:Block diagonalization and the energy-momentum method，Phys.Rep.193（1990）279-360.http://dx.doi.org/10.1016/0370-1573（90）90125-L.

［12］C.A.Woolsey，Reduced Hamiltonian dynamics for a rigid body/mass particle system，J.Guid.Control Dyn.28（2005）131-138. http://dx.doi.org/10.2514/1.5409.

［13］N.E.Leonard，J.E.Marsden，Stability and drift of underwater vehicle dynamics: Mechanical systems with rigid motion symmetry，Physica D 105（1997）130-162.http://dx.doi.org/10.1016/S0167-2789（97）83390-8.

［14］N.E.Leonard，Stability of a bottom-heavy underwater vehicle，Automatica 33（1997）331-346.http://dx.doi.org/10.1016/S0005-1098（96）00176-8.

［15］D.V.Zenkov，A.M.Bloch，J.E.Marsden，The energy-momentum method for the stability of non-holonomic systems，Dyn.Stab.Syst.13（1998）123-165. http://dx.doi.org/10.1080/02681119808806257.

［16］G.Rein，J.Vukadinovic，P.Braasch，Nonlinear stability of stationary plasmas—an extension of the energy-Casimir method，Siam J.Appl.Math.59（1998）831-844.

［17］T.R.Kane，R.Ryan，A.K.Banerjee，Dynamics of a cantilever beam attached to a moving base，J.Guid.Control Dyn.10（1987）139-151. http://dx.doi.org/10.2514/3.20195.

［18］A.M.Bloch，Stability analysis of a rotating flexible system，Acta Appl.Math.15（1989）211-234.http://dx.doi.org/10.1007/BF00047531.

［19］G.Cheng，Y.Z.Liu，Attitude stability of liquid-filled satellite with flexible appendage in gravitational field，Chin.J.Space Sci.17（1997）367-371.（in Chinese）.

［20］J.L.Kuang，K.L.Huang，The nonlinear stability of the liquid-filled satellite with four-flexible-attachments using the energy-Casimir method，Acta Aeronaut. Astronaut.Sin.15（1994）433-439（in Chinese）.

［21］B.Z.Yue，A.Salman，X.J.Song，Casimir method for attitude stability analysis of liquid-filled spacecraft，Sci.Sinica.Ser.A.43（2013）401-406. http://dx.doi.org/10.1360/132012-689.in Chinese.

［22］A.Salman，B.Z.Yue，Bifurcation and stability analysis of the Hamiltonian casimir model of liquid sloshing，Chin.Phys.Lett.29（2012）060501. http://dx.doi.org/10.1088/0256-307X/29/6/060501.

［23］K.Dong，N.M.Qi，X.L.Wang，et al.，Dynamic influence of propellant sloshing estimation using hybrid:Mechanical analogy and CFD，Trans.Japan Soc. Aeronaut.Space.Sci.52（2009）144-151.

［24］Y.H.Jia，S.J.Xu，R.Nie，Modeling and dynamics analysis of liquid-filled flexible spacecraft，J.Beijing Univ.Aeronaut.Astronaut.29（2003）35-38.（in Chinese）.

［25］W.Hu，Q.Tian，H.Y.Hu，Dynamic simulation of liquid-filled flexible multibody systems via absolute nodal coordinate formulation and SPH method，Nonlinear Dyn.75（2014）653-671.http://dx.doi.org/10.1007/s11071-013-1093-3.

［26］D.L.Peng，Dynamic model and variable structure control for flexible fuel-filled spacecraft，IEEE Pap.（2006）2067-2071. http://dx.doi.org/10.1109/TENCON.2005.301029.

［27］B.Pridgen，K.Bai，W.Singhose，Shaping container motion for multimode and robust slosh suppression，J.Spacecr.Rockets 50（2013）440-448. http://dx.doi.org/10.2514/1.A32137.

［28］D.D.Yang，B.Z.Yue，W.J.Wu，etal.，Attitudemaneuverofliquid-filledspacecraft with a flexible appendage by momentum wheel，Acta Mech.Sin.28（2012）543-550.http://dx.doi.org/10.1007/s10409-012-0060-4.

［29］B.N.Agrawal，Stability of spinning spacecraft with partially liquid-filled tanks，J.Guid Control.Dyn.5（1982）344-350.http://dx.doi.org/10.2514/3.56181.

［30］H.F.Bauer，W.Eidel，Liquid oscillations in a prolate spheroidal container，in:Nasa Sti/Recon Technical Report N，1988.

［31］F.T.Dodge，Thenewdynamicbehaviorofliquidsinmovingcontainers，in:Nasa Sti/Recon Technical Report N，2000.

5 January 2016

.

E-mail address:bzyue@bit.edu.cn（B.Yue）.

http://dx.doi.org/10.1016/j.taml.2016.03.001

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

in revised form

*This article belongs to the Dynamics and Control