Elastic properties of chiral，anti-chiral，and hierarchical honeycombs: A simple energy-based approach

Dvood Mousnezhd，Bk Hghpnh，Rnjy Ghosh，Adel Mgid Hmoud，Hmid Nye-Hshemi，Ashkn Vziri，∗

aDepartment of Mechanical and Industrial Engineering，Northeastern University，Boston，MA 02115，USA

bMechanical and Industrial Engineering Department，Qatar University，Doha，Qatar

Elastic properties of chiral，anti-chiral，and hierarchical honeycombs: A simple energy-based approach

Davood Mousanezhada，Babak Haghpanaha，Ranajay Ghosha，Abdel Magid Hamoudab，Hamid Nayeb-Hashemia，Ashkan Vaziria，∗

aDepartment of Mechanical and Industrial Engineering，Northeastern University，Boston，MA 02115，USA

bMechanical and Industrial Engineering Department，Qatar University，Doha，Qatar

H i G H L i G H T s

•Effects of chirality and hierarchy on elastic response of honeycombs are studied.

•Closed-form relations are derived for elastic moduli and validated using finite element method（FEM）.

•Chirality always decreases the stiffness and Poisson’s ratio.

•Hierarchical refinement increases the stiffness in hexagon based honeycombs.

•Anti-tetra-chiral structure shows anisotropy，auxeticity，and low shear stiffness.

A R T i C L Ei N F O

Article history:

26 February 2016

Accepted 29 February 2016

Available online 11 March 2016

Chiral

Hierarchical

Honeycomb

Metamaterial

Auxetic

The effects of two geometric refinement strategies widespread in natural structures，chirality and self-similar hierarchy，on the in-plane elastic response of two-dimensional honeycombs were studied systematically.Simple closed-form expressions were derived for the elastic moduli of several chiral，antichiral，and hierarchical honeycombs with hexagon and square based networks.Finite element analysis was employed to validate the analytical estimates of the elastic moduli.The results were also compared with the numerical and experimental data available in the literature.We found that introducing a hierarchical refinement increases the Young’s modulus of hexagon based honeycombs while decreases their shear modulus.For square based honeycombs，hierarchy increases the shear modulus while decreasing their Young’s modulus.Introducing chirality was shown to always decrease the Young’s modulus and Poisson’s ratio of the structure.However，chirality remains the only route to auxeticity.In particular，we found that anti-tetra-chiral structures were capable of simultaneously exhibiting anisotropy，auxeticity，and remarkably low shear modulus as the magnitude of the chirality of the unit cell increases.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

Among the most readily observed topological features in naturalstructuresarechirality［1-5］，hierarchy［6-13］，andhierarchyof chirality［14，15］.Their abundance in nature can be contrasted with traditional man-made constructions，which often rely on multiple materials selection but relatively simpler micro-geometrical constitution.In recent years，following these topological cues，synthetic metamaterials with non-traditional properties such as negative stiffness［16-18］，auxeticity［19-22］，and negative thermal expansion［23-25］have been proposed.These characteristics make mechanical metamaterials suitable for applications such as novel prostheses［26］，fasteners［27］，piezo-composites with optimal performance［28］，dome-shaped panels［29，30］，and high structural integrity foams［31］.

Among this general class of metamaterials，periodic chiral lattices such as the ones shown in Fig.1 have been shown to possess relatively compliant behavior because of their bending dominated response，while exhibiting considerable multiaxial expansion/contraction under uniaxial loads due to auxeticity［32，33］.These features make them optimal candidates for flexible design applications such as micro-electro-mechanical-systems（MEMS）［19，34，35］，aircraft morphing structures［36-43］，and as analogues of spokes in non-pneumatic tires［44，45］.In addition，chiral honeycombs have been experimentally and numerically shown to possess Poisson’s ratios in the range of-1＜ν＜0.For instance，Alderson et al.［46］studied the in-plane elasticconstants of chiral and anti-chiral honeycombs using finite element（FE）analysis and experiments.Continuing further，Alderson et al.［47］investigated the in-plane linear elastic response and out-of-plane bending of tri-and anti-tri-chiral honeycombs and their re-entrant counterparts using FE analysis and experiments.Nonetheless，closed-form expressions of elastic moduli for most of these structures are still unavailable.Among several twodimensional（2D）chiral lattices proposed in the literature，only the elastic properties of hexa-and tetra-chiral lattices have been investigated analytically，using micro-polar and second-gradient continuum theories［32，48-51］.These approaches are far more complex than the simple yet robust method used here for analytical study of chiral unit cells，which often require special boundary conditions at the unit cell level due to underlying rotational symmetry of the structure.

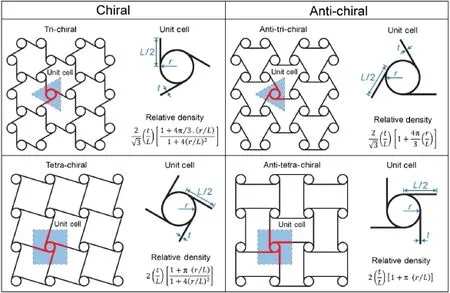
Fig.1.Schematic of the structure and the unit cell，and the expression of relative density for the chiral and anti-chiral honeycombs studied.

Another class of bio-inspired materials used increasingly to broaden the achievable range of mechanical response is the hierarchically structured material systems.Extreme values of material propertiessuchasspecificstiffness［11，52-54］，toughness［55-58］，strength［11，53，59，60］，bucklingstrength［61］，negativeorcomplex Poisson’sratio［62-65］，andphononicbandgaps［66］havebeenreported in hierarchical architectures across multiple length scales. Through a series of studies on the strength of different fractallike structures under various loads，Farr and co-workers［59，67-70］suggested that the volume of the material used for a stable structure can be reduced by an order of 3-4 under mild loads using hierarchical designs of third and fourth generation.However，the advantage of hierarchical design in these structures diminishes as the magnitude of applied loading increases.Ajdari et al.［52］showed that a type of self-similar hierarchical honeycomb is capable of attaining specific Young’s modulus as much as 2 and 3.5 times that of a regular hexagonal lattice through first and second orders of hierarchy，respectively.In a more inclusive study thatconsideredenhancementsinmultipleparameters，Haghpanah et al.［71］showed that a wide range of specific stiffness and strength can be tailored by introducing higher orders of hierarchy in a hexagonal lattice.However，none of these earlier studies specifically focused on investigating the geometry of hierarchy as a controlling variable of mechanical properties of honeycombs. Moreover，there is no systematic comparison between hierarchy and chirality in the literature，which can be useful in design and selection of structures for different loading conditions.

In light of this discussion，it becomes clear that further investigations on the behavior of these classes of metamaterials are well justified.Particularly，obtainingclosed-formanalyticalexpressions for the elastic constantsin terms of geometric and material parameters would constitute an important step towards evaluating and designing these materials.Furthermore，it would also foster a better understanding of the role of chirality and hierarchy in influencing the mechanical response of these materials.To this end，in the current paper，we carry out a systematic theoretical and computational study of the effects of these two natural geometrical organizations—chirality and hierarchy—on the in-plane elastic response of 2D honeycombs.In order to directly compare the effects of chirality versus hierarchy，we limit the results to first order of hierarchy for the hierarchical structures presented here. An energy-based method is used to obtain the unit cell deformation by satisfying both the periodic boundary conditions and symmetry requirements for the unit cell.Two specific types of regular tessellation with square and hexagonal cells are altered to endow them with chirality and hierarchy.For achieving chirality，the square based unit cell is altered to yield two different types of chiral architectures—tetra-chiral and anti-tetra-chiral—whereas the hexagonal unit cell alteration results in tri-chiral and anti-tri-chiral structures（illustrated in Fig.1）.In contrast to chiral microstructures，hierarchy is achieved by both conserving the rotational and reflective symmetries of the lattice.This is done by replacing the nodes in a periodic network of cells with the original cells albeit of smaller size as shown in Fig.2.Thus，the introduction of hierarchy into the square unit cell results in hierarchical square and hierarchical diamond honeycombs（illustrated in Fig.2）.In order to proceed with our calculations，the representative volume element（RVE）is used as the fundamental unit of analysis.In a periodic lattice material，the RVE（i.e.，unit cell）is identified as the smallest volume which with associated tractions anddisplacements，tessellatesthespacetorepresentthewholelattice structure under loading［60］.We choose the shaded triangular and square areas bounded by dashed lines in Figs.1 and 2 asthe structural unit cells of the structures under study.This implies that under any in-plane loading，we can tile the 2D space，solely by translating，and/or reflecting，and/or rotating（by 180°）the unit cells and their corresponding tractions and displacements，to represent the infinitely extended 2D structures.

Fig.2.Schematic of the structure and the unit cell，and the expression of relative density for the hierarchical honeycombs studied.

Wefirstdescribeandderivetheelasticmoduli（i.e.，Young’sand shear moduli，and Poisson’s ratio）of chiral and anti-chiral structures.This is followed by a section devoted to deriving the elastic constants for the hierarchical structures.The results are then compared in a unified template to highlight the effects brought about by these geometrical variants.The paper ends with conclusions.

Chiral and anti-chiral structures studied in this paper have an array of cylinders（nodes）connected by tangential ligaments（ribs）as shown in Fig.1.Depending on the number of ligaments tangential to each cylinder，two types of chiral lattices are introduced:tri-and tetra-chiral structures which are respectively composed of 3 and 4 tangential ligaments for each cylinder. Similarly，anti-chiral lattices are generated if any two adjacent cylinders share the same side of the common tangential ligament. Thus，in addition，two anti-chiral lattices are introduced which are called anti-tri-and anti-tetra-chiral structures（see Fig.1）.

The structural organization of the chiral and anti-chiral honeycombs can be defined by the ratio，r/L，where r is the radius of the cylinders and L is the length of the ligaments as described in Fig.1.Thisfigurealsorepresentsthedimensionlessrelativedensity（i.e.，area fraction）of the structures in terms of r/L and t/L，where t is the thickness of the cell walls.For the special case，where r= 0，the normalized relative density of the hexagon（tri-chiral and anti-tri-chiral）andsquare（tetra-chiralandanti-tetra-chiral）based chiral and anti-chiral honeycombs respectively reduce to that of regular hexagonaland square（2t/L）honeycombs.

Here，we derive closed-form expressions for elastic properties of chiral and anti-chiral honeycombs made of an isotropic linear elastic material with Young’s modulus，Es.In contrast to the previous studies［32，33，48-51］，we employ a simple energy-based procedure（Castigliano’s second theorem［72］）to obtain analytical estimates for elastic properties of the structures under study. A three-fold symmetry seen within the tri-and anti-tri-chiral lattices（see Fig.1）assures the macroscopic isotropy of their in-plane elasticproperties［73］.Thus，forcompletecharacterizationofthese structures，they each need only two elastic constants to be determined（i.e.，Young’s modulus and Poisson’s ratio）（shear modulus is obtained as a function of the other two elastic constants，analogous to isotropic materials）.In principle，these elastic constants canbedeterminedbyanykindofin-planeloading.However，inthis study，without loss of generality we chose uniaxial loading to obtain the Young’s modulus and Poisson’s ratio.In contrast，the fourfold symmetry of tetra-and anti-tetra-chiral honeycombs causes the structures to exhibit macroscopic anisotropy in their in-plane elasticbehavior.Therefore，allthecomponentsoftheirstiffness（or compliance）tensor have to be determined in order to fully identify their elastic behavior.For tetra-and anti-tetra-chiral lattices，we first chose a coordinate system such that the x and y axes were aligned to the lines connecting the center of adjacent cylinders together.This symmetry requires one Young’s modulus，one Poisson’s ratio，one shear modulus，and possibly two more coefficients called‘the coefficients of mutual influence of the first kind’［74］（they characterize the normal strains caused by shear stresses）.

To this end，for each of the anisotropic honeycombs（tetra-and anti-tetra-chiral structures），we first impose a uniaxial loading in the x-direction（i.e.，horizontal direction in Fig.1）to obtain the structure’s Young’s modulus，Ex，and Poisson’s ratio，νxy.Note that the sub-index x，is used to emphasize that the elastic constants are obtained as a result of a loading in the x-direction and they are not valid for any other directions（except for y-direction（i.e.，vertical direction in Fig.1），due to symmetry）of in-plane loading since the structuresdonothaveanisotropicin-planebehavior.Furthermoredue to this anisotropy，in order to obtain the shear modulus，Gxy，and the coefficients of mutual influence of the first kind，we apply a separate shearing load to these structures.It is noteworthy that since these structures are stretching dominated in both the x-and y-directions，we must include the stretching terms in addition to bending terms in computing the strain energy of the unit cells. In contrast，for bending dominated structures，we only include the bending terms of strain energy.In our theoretical calculations，the central cylinders appearing in the unit cells are regarded as perfectly rigid elements.Also the rotation of ligaments and cylinders is neglected due to small deformation assumption.These assumptions significantly reduce the complexity of the problem yielding closed-form expressions for elastic moduli while staying reasonably accurate for most of the geometries considered in this study.

Fig.3.（a）Schematic of a tetra-chiral honeycomb under x-direction uniaxial loading.（b）Free body diagram of the structural unit cell under uniaxial loading.（c）Schematic of a tetra-chiral honeycomb under x-y shearing load.（d）Free body diagram of the structural unit cell under shearing load.

In the next paragraphs，we will derive closed-form expressions for the elastic moduli of tetra-chiral structures as a demonstration of our proposed method.The detailed derivations for other chiral and anti-chiral structures are presented in Appendices.

A schematic of a tetra-chiral structure，which is based on an underlying square network，undergoing a uniaxial far-field stress in the x-direction，σxis shown in Fig.3（a）.The free body diagram（FBD）of the corresponding unit cell is shown in Fig.3（b）.The unit cell contains a cylinder（node）which is assumed to be rigid and four half ligaments.Due to the 180°rotational symmetry of the structure and the components of the microscopic stresses，all four external cut points of the unit cell（i.e.，points 1 through 4 in Fig.3（b））must be moment-free under an arbitrary macroscopic stress state.Also，since the only far-field stress acting on the structure is along the x-direction，all the external cut points must be force-less except points 1 and 2 which carry a pair of forces with opposite directions along the x-direction due toσx.Therefore，unknown forces and moments acting on the unit cell’s external cut points can be summarized as shown in Fig.3（b），where F can be determined as a function of applying stress as，F=σxR，where R is the center to center distance between any two adjacent cylinders. Moreover，to be able to determine the structure’s Poisson’s ratio，a pair of virtual forces，P is also added on points 2 and 4 of the unit cell.The strain energy of the unit cell is given as:

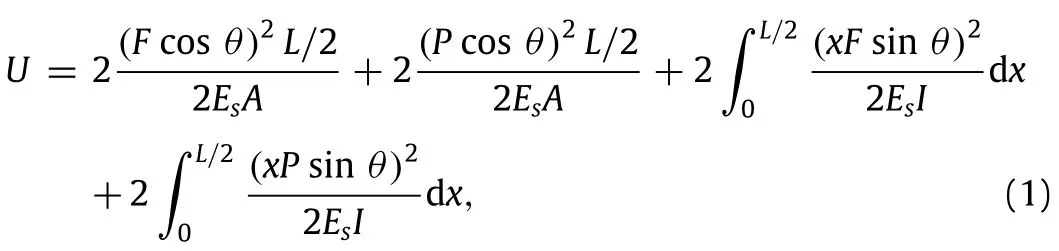
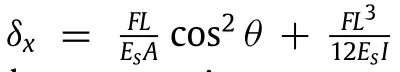
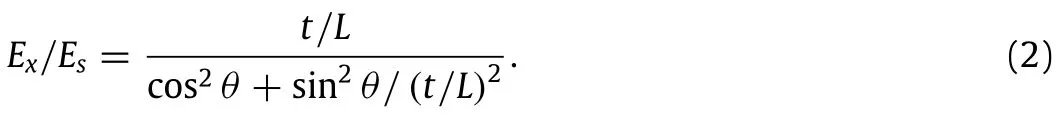
On the other hand，∂U/∂P|P=0gives the total displacement of points2and4inthedirectionofvirtualforcesasδy=0.Therefore，ϵy=δy/R=0 and this will result inνxy=0.

In the next step，we seek to determine the structure’s shear modulus with respect to the x-y coordinate system.To this end，we consider a tetra-chiral structure undergoing a uniform far-field shear stress，τxy，as shown in Fig.3（c）.FBD of a representative unit cell is also shown in Fig.3（d）.The 180°rotational symmetry of the structure implies unit cell’s all four external cut points（i.e.，points 1 through 4 in Fig.3（d））to be moment free.Furthermore，each of these external cut points must be free of any normal forces（in the direction passing through the cut point and center of the cylinder），because there is no macroscopic normal stress acting on the structure in those directions.Thus，there are only four equal shearing forces acting on the unit cell’s external cut points，F，which can be obtained as a function of applying stress as，F=τxyR. We also apply two pairs of virtual forces，Px，and Pyto the unit cell to be able to find the average strains in the x-and y-directions due to the applying shear stress.Therefore，based on the loadings on the unit cell shown in Fig.3（d），the strain energy is given as the following:

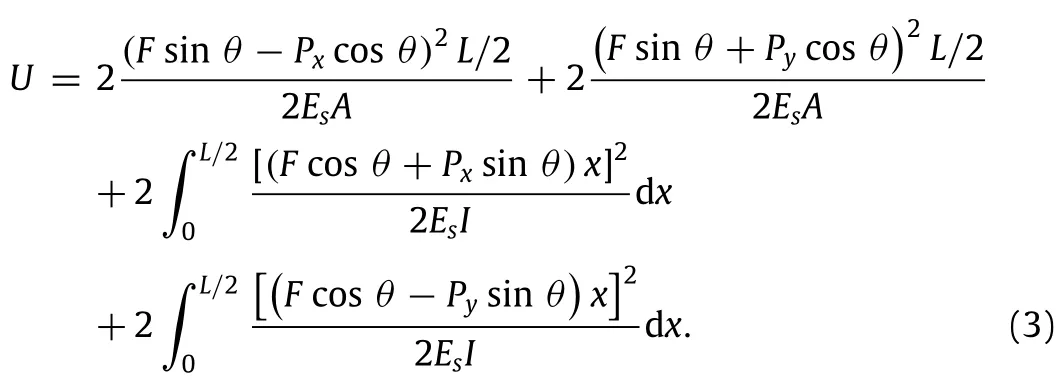
Next，（∂U/∂F|Px=Py=0）/R gives the total change of angle between two straight lines initially parallel to the x-and y-axes which is the direct measure of the shear strain，γxy.Then，the shear modulus of the structure normalized with respect to the Young’s modulus of cellwallmaterial，isdefinedastheratiooftheaverageshearstress，τxyto the average shear strain，γxyand given as the following:

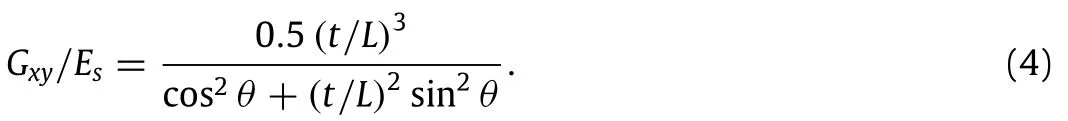
Note that asθgoes to zero，the structure transforms into a regular square honeycomb.Upon substitutingθ=0 into the closed-form expressions for Exand Gxy，we obtain Ex/Es=t/L，and Gxy/Es= 0.5（t/L）3，which are the Young’s and shear moduli of a regular square honeycomb，respectively［75］.For all values ofθ，Poisson’s ratio is equal to that of square honeycomb，νxy=0.

From the above calculations，the structure’s 2D compliance tensor can be formed as the following:

where S11=S22=1/Ex，S12=-νxy/Ex，and S33=1/Gxy. Then，to completely determine all components of 2D compliance tensor of this structure，we still need to obtain S13and S23，which can respectively be given by calculating the average normal strains of the structure in the x-and y-directions due to the shearing load.give the average normal strains in the x-and y-directions（ϵxandϵy），respectively.Then，S13and S23are respectively defined as the ratio of the resulting normal strains in the x-and y-directions to the applying shear stress and given as the following:

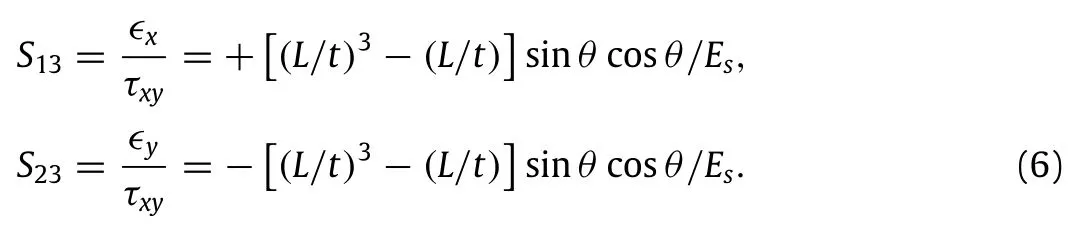
Next，inordertofindtheorientationofprincipalcoordinatesystem（i.e.，directions in which S13and S23are both equal to zero which implies that no normal strains can be produced under shear stress） we rotate the x-y-z coordinate system with respect to the z-axis by an angleα（positive when counter-clockwise）.The compliance tensor in the new system，¯S is determined using the compliance transformation rule［74］，¯S=TSTT，where T is the rotation tensor defined as:

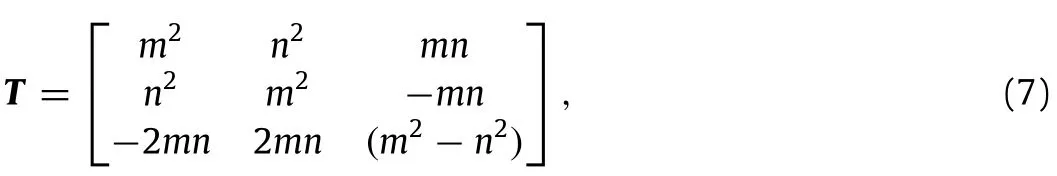
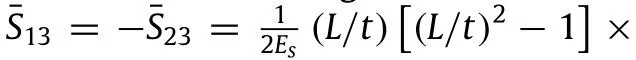
Similar procedure has been performed to obtain closed-form expressions of elastic moduli for tri-，anti-tri-，and anti-tetra-chiral structures and the details have been presented in Appendices.

In this section，we investigate the linear elastic properties of hierarchical structures.To this end，we select two representative samples，hierarchical square and hierarchical diamond，which are respectivelygeneratedbyreplacingtheverticesofaregularsquare honeycomb by smaller squares and diamonds（see Fig.2）.The wall thickness of the structures is simultaneously reduced to maintain the overall density equal to that of regular square honeycomb.

Similar to chiral and anti-chiral honeycombs，the structural organization of hierarchical structures can be defined by the ratio，r/L，where r and L are defined for each structure in Fig.2. This figure also represents the dimensionless relative density（i.e.，area fraction）of the structures in terms of r/L and t/L.For the special case，where r=0，the normalized relative density of the hexagon（hierarchical hexagonal honeycomb），and square（hierarchical square and hierarchical diamond）based hierarchical structures respectively reduce to that of regular hexagonal（t/L）］，and square（2t/L）honeycombs.

Note that among these three hierarchical structures shown in Fig.2，Ajdari et al.［52］studied the in-plane elastic properties of hierarchical hexagonal honeycombs.Thus，in the current paper we focus on the other two structures and just report the results published by the authors for the sake of completeness.

Similar to the previous section，Castigliano’s second theorem is used to derive closed-form relations for elastic properties of hierarchical structures made of an isotropic linear elastic material with Young’s modulus，Es.It should be noted that hierarchical square and diamond structures exhibit macroscopic anisotropy. Thus，in order to completely characterize their elastic behavior we need to obtain the Young’s modulus，Poisson’s ratio，and shear modulus along the principal directions.To this end，first a uniaxial loading in the x-direction is applied to each structure to determine the structure’s Young’s modulus，Exand Poisson’s ratio，νxyand then a shearing load is imposed to obtain the shear modulus，Gxy. Finally the orientation of principal coordinate systems is given for each structure.In contrast to chiral and anti-chiral lattices where we assumed the cylinders to be rigid，here we assume the entire structure including smaller squares and diamonds to have a linear elastic material property.

Wewillobtainclosed-formexpressionsoftheelasticmodulifor hierarchical square structures as a demonstration of our proposed method.The details of the procedure for hierarchical diamond structures are presented in Appendices.

A schematic of a hierarchical square honeycomb under a uniaxial far-field stress in the x-direction，σxis shown in Fig.4（a）.A detailed FBD of the structural unit cell of this structure is shown in Fig.4（b）.It contains a smaller square and four half ligaments connecting the smaller squares together.Due to 180°rotational symmetry of the structure and components of microscopic stress，all external cut points of the unit cell（i.e.，points 1 through 4 inFig.4（b））mustbemomentfree.Furthermore，byusingacutline∆1，we can see that since there is no macroscopic stress on the structureinthey-direction，theunitcellmustbefreeofanyforcesinthe y-direction at point 4.Similar arguments also hold true for point 2. Alsonotethatthestructureissymmetricwithrespecttoallfourcut lines shown in Fig.4（a）.This implies that the component of forces parallel to these cut lines at corresponding external cut point must be equal to zero.Thus，under the uniaxial stress on the structure，σx，each unit cell experiences the loading shown in Fig.4（b），where F can be obtained as a function of applied stress as，F=σxL.

Fig.4.（a）Schematic of a hierarchical square honeycomb under x-direction uniaxial loading.（b）and（c）Free body diagram of the structural unit cell under uniaxial loading，where P is a virtual force used for Poisson’s ratio calculations.（d）Schematic of a hierarchical square honeycomb under x-y shearing load.（e）Free body diagram of the structural unit cell under shearing load.

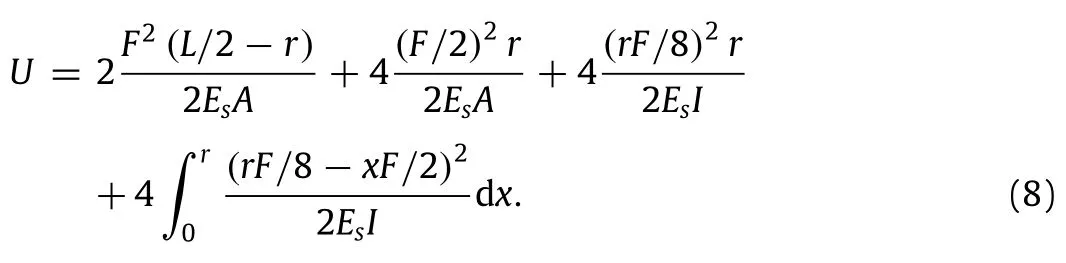
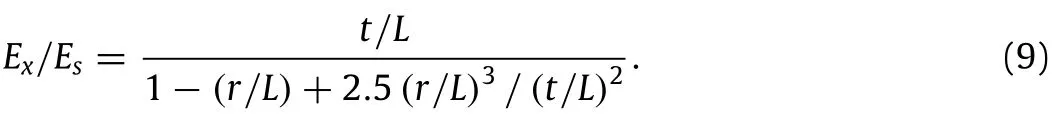
Next，in order to calculate the Poisson’s ratio，let us consider a pair of virtual forces acting on the unit cell in the lateral direction，as shown in Fig.4（c）.One fourth of the smaller square of this unit cell is also shown in Fig.4（c）.Similar procedure as employed earlier is used to determine the unknown moments，M1and M2，acting on points 6 and 7 as M1=rF/8-3rP/8 and M2=rP/8-3rF/8. Thus，the strain energy of the unit cell is given as:

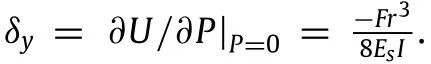
Finally，to determine the shear modulus，as shown in Fig.4（d），we apply a uniform far-field shear stress，τxyto the structure.A FBD of the unit cell of the structure is also shown in Fig.4（e）.The 180°rotational symmetry of the structure implies unit cell’s all four external cut points（i.e.，points 1 through 4 in Fig.4（e））to be moment free.Furthermore，each of these external cut points must be free of any normal forces（in the direction of the ligament），because there is no macroscopic normal stress acting on the structure in those directions.Thus，there are only four equal shearing forces acting on the unit cell’s external cut points，F，which can be obtained as a function of applying stress as，F=τxyL.Next，consider one fourth of the smaller square as shown in Fig.7（e）.Using the equilibrium equations，components of unknown forces and momentactingontheexternalcutpointsofthisportionoftheunitcell can be determined as functions of F，as shown in Fig.4（e），where M=（F/2）·（L/2-r）.Hence，the strain energy of the unit cell can be written as:

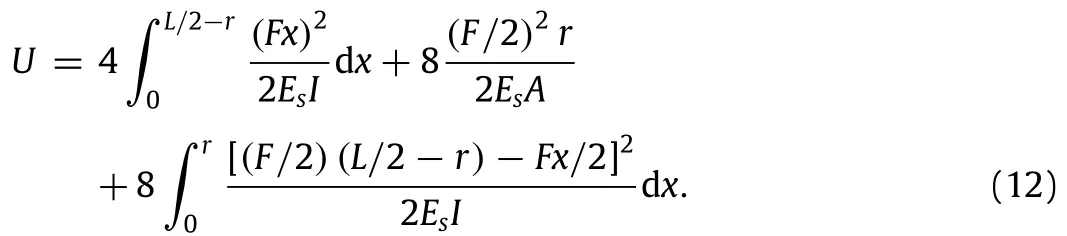
Then，（∂U/∂F）/L gives the total change of angle between two straight lines initially parallel to the x-and y-axes（i.e.，the shear strain，γxy）.Finally，shear modulus of the structure（Gxy，normalized with respect to the Young’s modulus of cell walls material）is defined as the ratio of the average shear stress，τxyto the average shear strain，γxyand obtained as the following:

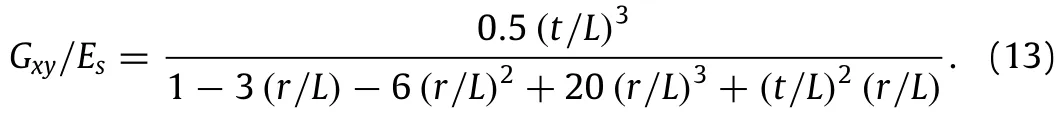
Note that as r goes to zero，the structure transforms into a regular square honeycomb.Upon substituting r=0 into Eqs.（9），（11）and（13），we obtain Ex/Es=t/L，νxy=0，and Gxy/Es=0.5（t/L）3，whicharetheYoung’smodulus，Poisson’sratio，andshearmodulus of a regular square honeycomb，respectively.The principal directions for the 2D compliance tensor（S13and S23are both equal to zero for the current x-y-z coordinate system）of this structure can be calculated as，α=kπ/4，where k is an integer.

Similar procedure has been performed to obtain closed-form expressions of elastic moduli for hierarchical diamond structures and demonstrated in detail in Appendices.

In order to validate the theoretical expressions of elastic moduli，FE-based numerical models were developed to conduct simulations on the structures.We carry out FE analysis at the structural level instead of the unit cell level with 2D models of the structures constructed using the FE software ABAQUS 6.11-2（SIMULIA，Providence，RI）.The relative characteristic length of the samples with respect to the unit cells was sufficiently large enough to mitigate boundary effects on the inner unit cells.The models were meshed using in-plane 2-node linear beam elements allowingforsheardeformation（i.e.，B21beamelementinABAQUS）and a mesh sensitivity analysis was carried out to guarantee that the results were not mesh-dependent.Static-general solver of ABAQUS was used to simulate the response of these structures under uniaxial compression and shearing loads.Cell walls were assumed to have a rectangular cross section with unit lengthnormal to the loading plane（i.e.，normal to the x-y plane）.R was taken to be equal to unity and the thickness（t）was adjusted to be consistentwiththevalueoftherelativedensitypresentedinFigs.1 and 2.Linear elastic properties of aluminum were assumed for the cell wall material with Es=70 GPa andνs=0.3.

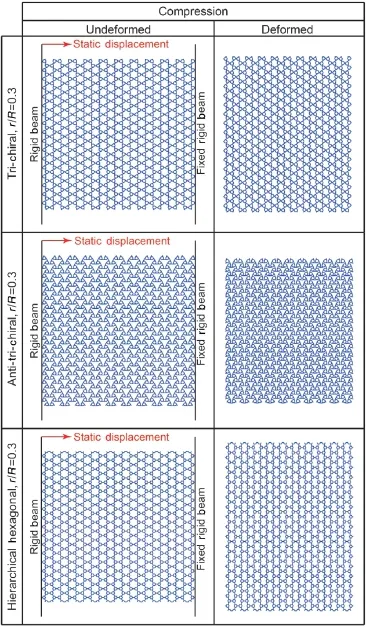
Fig.5.Schematic diagrams of the FE models constructed in ABAQUS for simulating static uniaxial loads，as well as their corresponding exaggerated deformed configurations，for the structures with hexagon based grids with r/R=0.3.

Figures 5 and 6 show the schematic diagrams of the FE models constructed in ABAQUS for simulating static uniaxial and shearing loads，as well as their corresponding exaggerated deformed configurations，for the structures with underlying hexagon and square based grids，respectively.In order to simulate the uniaxial loading，constant static displacement was assigned to the left nodes（see Figs.5 and 6），while the horizontal displacement of the right nodes was constrained（i.e.，set to zero）.Then，to eliminate any boundary effects，periodic boundary conditions were imposed on the structures on the top-and bottom-side nodes［76］.Also note that the vertical displacement of an arbitrary node was constrained（i.e.，set to zero）in order to prevent rigid body motion of the structure in that direction.To simulate the square based honeycombsundershearingloads，shearforceswereappliedtothe boundarynodes，whilethehorizontalandverticaldisplacementsof an arbitrary node were constrained（i.e.，set to zero）to avoid rigid body motion，Fig.6.

Fig.6.Schematic diagrams of the FE models constructed in ABAQUS for simulating static uniaxial and shearing loads，as well as their corresponding exaggerated deformed configurations，for the structures with square based grids with r/R=0.3.

The analytical expressions of effective Young’s modulus（Young’s modulus of the structure normalized by cell wall material’s Young’s modulus），Poisson’s ratio，and effective shear modulus（shear modulus of the structure normalized by cell wall material’s Young’s modulus）for the meta-lattices studied are tabulated in Tables 1 and 2.In Table 1，the structures are characterized into two categories—hexagon and square based honeycombs. The structural unit cell，effective Young’s modulus，and Poisson’s ratio for each structure are reported in the next columns.For anisotropic structures（i.e.，square based honeycombs），the effective shear modulus and material principal directions are reported in Table 2.

In Fig.7，we plot the normalized Young’s modulus（effective Young’s modulus of the structure normalized by the effective Young’s modulus of a regular hexagonal honeycomb with same relative density）（Fig.7（a））and the Poisson’s ratio（Fig.7（b））of hexagon based chiral and hierarchical honeycombs varied via the r/R ratio which is a de-facto measure of the magnitude of alteration to the underlying structure.The solid lines represent the results from the analytical estimates of elastic moduli in Table 1 and markers denote the FE results.Note that Fig.7（a）is a log-log plot. Clearly as r/R→ 0，the chiral and hierarchical structures reduce trivially to the regular hexagonal honeycomb.A good agreement is observed between the theoretical and FE results except for trichiralstructurewherethetheorypredictshigherstiffnessandnegative Poisson’s ratio when r/R＞0.2.This discrepancy is resulted from the assumed rigid behavior for the cylindrical components in the chiral structures.When r/R→ 0.5 in the tri-chiral structure，the cylindrical components become the only source of compliance for the structure as straight beams vanish，and therefore the theoretical results diverge from the FE results.Among the hexagon based structures，hierarchical hexagonal honeycomb shows higher stiffness with respect to the other structures and the normalized Young’s modulus achieves the maximum value of¯E～=2 at r/R～= 0.32［52］.Theplot ofPoisson’s ratioshown inFig.7（b）also shows a good agreement with the theoretical derivations presented earlier. Unlike the hierarchical structure，the chiral and anti-chiral structures are capable of showing auxetic behavior（i.e.，negative Poisson’sratio）athigherr/Rvalues.Theanti-tri-chiralstructurewhichis also the most compliant among the three exhibits auxeticity as Poisson’s ratio becomes negative for r/R greater than～=0.2.

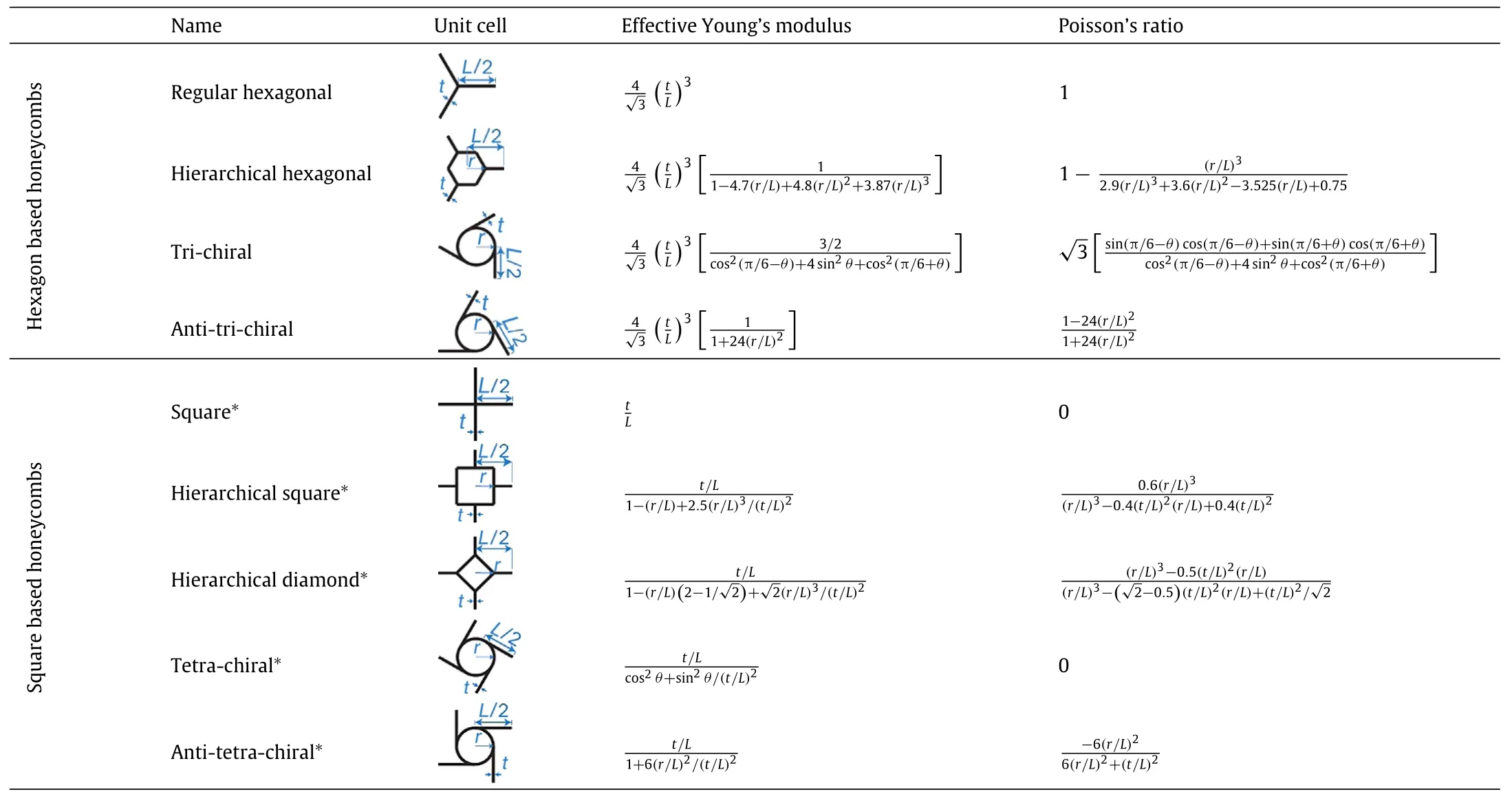
Table 1 Summary of the analytical relations for the effective Young’s modulus and Poisson ratio of cellular lattices studied in this article.Asterisks（*）highlight anisotropic lattices. For these anisotropic lattices the analytical expressions for the effective shear modulus and material principal directions are given in Table 2.

Table 2 Summaryoftheanalyticalexpressionsfortheeffectiveshearmodulusandmaterialprincipaldirectionsfortheanisotropiclatticesstudied.

Figure 8 illustrates the behavior of square based structures which are anisotropic.Since the results for stretching dominated honeycombs depend on the relative density of the structures，we reportedtheresultsofsquarebasedhoneycombsonlyataconstant relative density of 6%.The solid lines in these figures represent the results from the closed-form estimates of elastic moduli from Tables 1 and 2，and markers denote the FE results.Similar to hexagon based honeycombs，there exist discrepancies between the theoretical and numerical results of square based structures in the case of chiral and anti-chiral lattices，which become more pronounced for tetra-chiral structure as r/R goes to 0.5.Again，these discrepancies stem from the assumed rigid behavior for the cylindrical components in the chiral and anti-chiral structures.We plot the normalized Young’s modulus of the structure（effective Young’s modulus of the structure normalized by the effective Young’s modulus of a square honeycomb with same relative density）in Fig.8（a）and notice a good agreement with FE results. Clearly，increasing r/R results in a sharp decrease in the inplane stiffness of these structures which is especially pronounced in tetra-and anti-tetra-chiral lattices.Of all the square based structures studied，only anti-tetra-chiral honeycombs exhibit auxeticity for all values of r/R.In this structure，the Poisson’s ratio starts to change quite appreciably with even small changes in r/R，then accelerates towards lesser values of r/R and finally reaches a plateau.On the other hand，although the tetra-chiral structure，along with the hierarchical structures show little initial sensitivity to the variations in r/R，at around r/R～=0.03，their behaviors begin to sharply diverge.The hierarchical structures show a rapid change followed by plateaus whereas the tetra-chiral structure starts with a slower variation which accelerates sharply as r/R→0.5 due to the effect of compliance of the cylinders as mentioned above.Finally Fig.8（c）plots the variation of normalized shearmodulus（effective shear modulus of the structure normalized by the effective shear modulus of a square honeycomb with same relative density）of these anisotropic structures.The normalized shear moduli of the two chiral and two hierarchical structures show little initial sensitivity to variation of r/R.However，soon at about r/R ～=0.01，these two groups diverge completely in opposite directions unlike previous elastic constants.The chiral structures show increasingly low normalized shear modulus as r/R is increased whereas an increase in r/R positively affects the normalizedshearmodulusofthehierarchicalstructures.Thetrendfor tetra-chiral structure changes course at an r/R of about 0.25 as the structure becomes increasingly stiff in shear，causing a rapid increase as r/R→0.5.

Fig.7.（a）Normalized Young’s modulus，and（b）Poisson ratio as a function of geometrical parameter，r/R，for three different hexagon based hierarchical and chiral lattices. The effective Young’s modulus of the structure is normalized by the effective Young’s modulus of a regular hexagonal honeycomb（r/R=0）with same relative density.The solid lines represent the results from the theoretical estimates（i.e.relations reported in Table 1），and circles show the FE results.

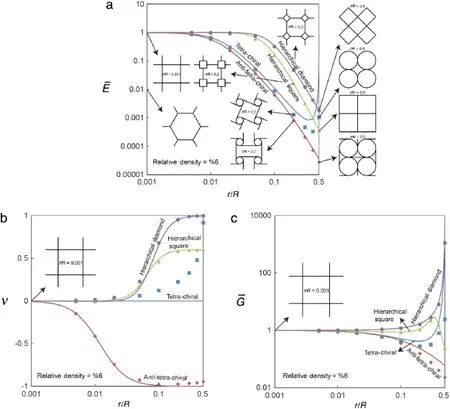
Fig.8.（a）Normalized Young’s modulus，（b）Poisson ratio，and（c）Normalized shear modulus as a function of geometrical parameter，r/R，for four different anisotropic square based hierarchical and chiral lattices.The effective Young’s and shear moduli of the structure are normalized by those of a square honeycomb（r/R=0）with same relative density.The solid lines represent the results from the theoretical estimates（i.e.relations reported in Tables 1 and 2），and circles show the FE results.

Table 3 Our theoretical and numerical results vs.numerical and experimental data available in Ref.［46］.

Next，we compare our results with numerical and experimental data available in the literature.We choose the reported data from Ref.［46］who carried out numerical and experimental analysis on the in-plane elastic properties of chiral and anti-chiral honeycombs subjected to uniaxial loading for small deformations.They employed selective laser sintering rapid-prototyping technique to fabricate the experimental samples out of nylon powder with geometrical parameters r=5 mm，L=25 mm，t=1.5 mm，and out-of-plane depth d=25 mm.Table 3 compares our results with their numerical and experimental data.From this table we find favorable comparisons of our elastic constants（Young’s modulus and Poisson’s ratio）for almost all chirality except the tetrachiral case.Note that some discrepancy is natural both due to the difference in the materials between the two cases and also from the different boundary conditions employed between the two FE models.Specifically，in contrast to our periodic boundary conditions imposed on the FE models at structural level，they employed slightly different non-periodic boundary conditions at the‘RVE level’which led to a stiffening effect on the RVEs.For instance，for tri-and anti-tri-chiral honeycombs，instead of applying appropriate forces and moments on the RVE’s edge nodes to simulate the uniaxial loading on a periodic structure，they used geometrical constraints（i.e.，couplinginteractionbetweenRVE’sedgenodes）to relate the displacements of particular edge nodes within the RVE. We believe that this difference may play an even greater role in the relatively large discrepancy between the results obtained for the case of tetra-chiral honeycombs.Interestingly，for this particular case，Alderson et al.［46］report auxeticity for this structure at small strains through both FE and experimental investigations（Table 3）whereas neither our theoretical prediction，nor FE simulations as seen in Fig.6 show any auxeticity for this case.

We studied the effects of chirality and hierarchy，generally a hallmark of natural materials，on the static in-plane properties of a selected set of 2D honeycombs.Analytical closed-form formulas for square and hexagon based networks have been obtained，and the results are verified numerically.Comprehensive design graphs，comparing elastic moduli（Young’s and shear moduli and Poisson’s ratio）are provided.We find that both chirality and hierarchy crucially affect the in-plane mechanical properties of these structures.Overall，hierarchical structures are stiffer and have higher Poisson’s ratio than their chiral counterparts for similar values of the r/R ratio which quantifies the amount of hierarchy or chirality.However，chirality remains the only route to auxeticity.This is due to the deformation mechanism observed in auxetic chiral and anti-chiral honeycombs.This mechanism is characterized by the rotation of cylindrical nodes and bending of the ligaments，which make the structures contract in the transversedirectionwhensubjectedtouniaxialcompressiveloads. The behavior of the elastic constants of anti-tetra-chiral structure shows a remarkable glimpse of an engineered material which can simultaneouslyexhibitanisotropy，auxeticity，andashearmodulus that is much lower than usual solids.

Acknowledgments

The authors thank Dr.Jim Papadopoulos for many fruitful discussions.Thisreport wasmadepossibleby aNPRP award（NPRP 7-882-2-326）from the Qatar National Research Fund（a member of the Qatar Foundation）.The statements herein are solely the responsibility of the authors.

Appendix A.Tri-chiral

A schematic of a tri-chiral honeycomb derived from a regular hexagonal architecture undergoing an in-plane uniaxial far-field（macroscopic）loading in the x-direction characterized by the normal stress，σxis shown in Fig.A.1（a）.A detailed FBD of the structural unit cell of this honeycomb is shown is Fig.A.1（b）.The unit cell contains a cylinder（node）which is assumed to be rigid and three half ligaments.Due to the 180°rotational symmetry of the structure and the components of the microscopic stresses，all three external cut points of the unit cell（i.e.，points 1 through 3 in Fig.A.1（b））must be moment-free under an arbitrary macroscopic stress state.Therefore，utilizing the equilibrium conditions of forces and moments，the horizontal force，F，can be related to the far-field stress as，，where R is the center to center distance of adjacent cylinders in the structure，as shown in Fig.A.1（b）.The vertical force，P is a virtual force which will be used later in this subsection to compute the Poisson’s ratio of the structure.Under the influence of this force system，neglecting the stretching and shearing terms，the strain energy stored in the unit cell of this bending dominated structure can be obtained as:

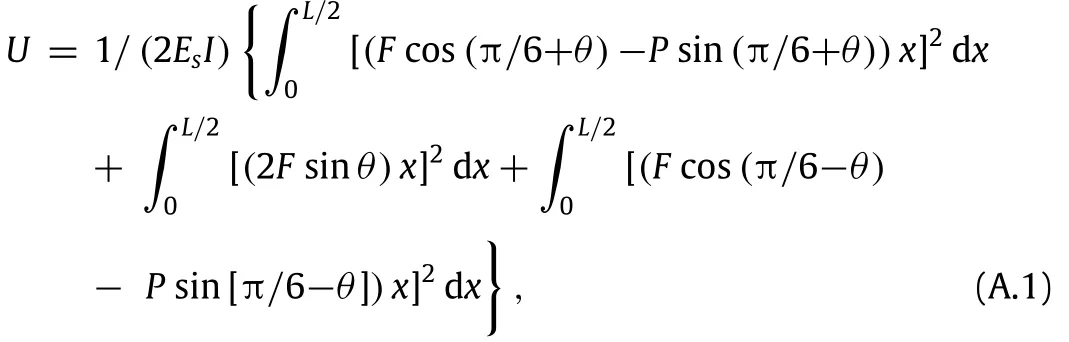
where Es（as mentioned earlier）is the Young’s modulus of the cell wall material，I is the second moment of area of the wall’s cross section（cell walls are assumed to have a rectangular cross section with uniform thickness，t，and unit depth，i.e.，I=t3/12），and θ=tan-1（2r/L）is the angle between each ligament and the line connecting the centers of two adjacent cylinders as shown in Fig.A.1（b）.Setting P=0 in Eq.（A.1）and using Castigliano’s second theorem［72］，∂U/∂F gives the total displacement（δx）of points 1 and 2（with respect to point 3）in the x-direction.Then the average strain of the structure in the x-direction is obtained by using the relation，ϵx=δx/（1.5R）.The effective Young’s modulus of the structure（normalized by material’s Young’s modulus，Es）is then defined as the ratio of the average stress，σx，and the average strain，ϵx，and obtained as:

Notethatasr goestozero，θalsoapproacheszeroandthestructure is reduced to a regular hexagonal honeycomb.Thus，lettingθ=0in Eq.（A.2）will result in，which is a familiar result for the effective Young’s modulus of a regular hexagonal honeycomb［75］.

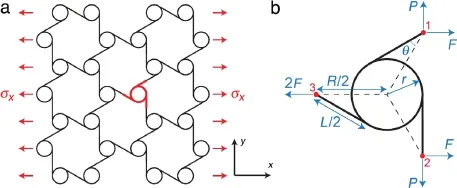
Fig.A.1.（a）Schematic of a tri-chiral honeycomb under x-direction uniaxial loading.（b）FBD of the structural unit cell.

Next，to completely characterize the elastic behavior of trichiral honeycomb，we also need to determine its Poisson’s ratio，ν.We again used Castigliano’s second theorem to obtain the displacement between points 1 and 2（δy）（see Fig.A.1（b））in the direction of the virtual forces as，Using this relation we obtainwhich gives the structure’s average strain in the y-direction due to the uniaxial loading，σxin the x-direction.The effective Poisson’s ratio，ν，of the structure is finally defined as the negative of the ratio of the average strain in the y-direction，ϵy，to the average strain in the x-direction，ϵx，and obtained as the following:

Again，note that as r goes to zero，Eq.（A.3）reduces toν = 1，which is the effective Poisson’s ratio of a regular hexagonal honeycomb［75］.

Appendix B.Anti-tri-chiral

A schematic of an anti-tri-chiral structure which is also derived from an underlying hexagonal unit cell architecture is shown in Fig.B.1（a）.An in-plane uniaxial far-field loading characterized by thenormalstress，σxisappliedtothestructureinthex-direction.A detailed FBD of the structural unit cell is also shown in Fig.B.1（b）. It contains a rigid cylinder（node）and three half ligaments.As shown in Fig.B.1（a），by using a cut line∆1，since there is no macroscopic stress to the structure in the y-direction，the unit cell must be free of any forces in the y-direction at point 1.Similar argument holds true for point 2（by using the cut line∆2in Fig.B.1（a））.Furthermore，due to the symmetry of the structure with respect to the cut line∆3（see Fig.B.1（a）），point 3 must also be free of any forces in the y-direction.Then，using the zigzag cut line∆4shown in Fig.B.1（a）and due to the symmetry of the structure mentioned above；points 1 and 2 must experience same forces in the x-direction and same moments with respect to the z-axis.Thus，the forces and moments acting on the external cut points of the unit cell are reduced as shown in Fig.B.1（b）（recall from previous section that the virtual force P has been applied to calculate the Poisson’s ratio and can be treated as zero in this part of the calculation）.Note that the x-component of the force applied to point 3（i.e.，2F）comes from the equilibrium of forces in the x-direction.Now，the equilibrium of moments in the z-direction gives 2M+M∗-3rF=0，where M and M∗are two yet unknown moments at external cut points of the unit cell as a result of the loading on the structure.Using this equation and neglecting the stretching and shearing terms，the strain energy stored in the unit cell is obtained as:

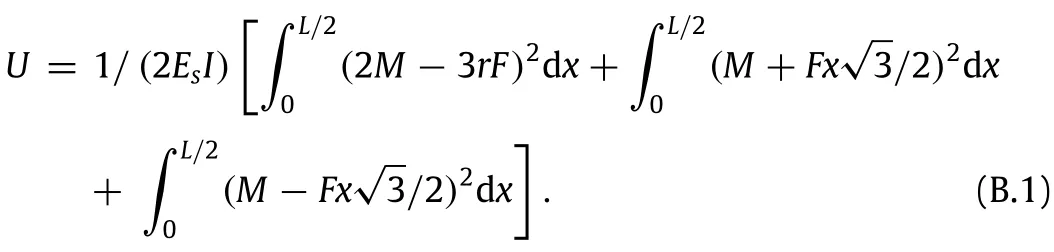
Now，for all horizontal lines of the structure to remain parallel in the deformed state，we can show that the following geometrical condition must hold:θ1=-θ2，whereθ1andθ2are respectively the total rotations of points 1 and 2 with respect to the z-axis.Using Castigliano’s theorem，this geometrical condition is equivalent to the relation，∂U/∂M=0.Now，substituting into this equation the strain energy given by Eq.（B.1），M is determined as a function ofF asM=rF.Alsousingequationofequilibriumforthemoments givenearlier，M∗isobtainedasM∗=rF.Next，substitutingthevalues obtained for unknown moments M and M∗into Eq.（B.1），the strain energy stored in the unit cell can be written as:

where F can be obtained as a function of the applying stress，σxas

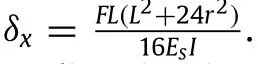
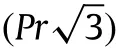
Fig.B.1.（a）Schematic of an anti-tri-chiral honeycomb under x-direction uniaxial loading.（b）FBD of the structural unit cell.

Next，we use Castigliano’s second theorem to obtain the total displacement of points 1 and 2（see Fig.B.1（b））in the direction of the virtual forces as，Using Eq.（B.4），δyis obtained as，Then，using this equation，ϵy=gives the structure’s average strain in the y-direction due to the uniaxial loading in the x-direction（σx）.The effective Poisson’s ratio，νof the structure is then defined as the negative of the ratio of the average strain in the y-direction，ϵyto the average strain in the x-direction，ϵxand given as follows:

Note that similar to the tri-chiral structure，here as r goes to zero，the structure transforms into a regular hexagonal honeycomb.Letting r=0 in Eqs.（B.3）and（B.5）will result inandν=1，which are the effective Young’s modulus and Poisson’s ratioofaregularhexagonalhoneycomb，respectively，asnotedearlier.

Appendix C.Anti-tetra-chiral

We now turn our attention to the next alteration of the square based unit cell which is an anti-tetra-chiral structure.Note that the Young’s modulus and Poisson’s ratio of the anti-tetra-chiral lattice with square and rectangle based networks have been analytically determined assuming the square based anti-tetrachirallattice（i.e.，whenallstraightbeamshavingidenticallengths）is macroscopically isotropic［33］.In contrast，in the current paper we will show that the square anti-tetra-chiral structure is macroscopically orthotropic（i.e.，having four-fold rotational symmetry and defined by three in-plane materials constants），and will derive analytical relations for the shear modulus and the material’s principal directions.

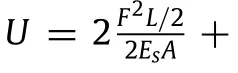
Fig.C.1.（a）Schematic of an anti-tetra-chiral honeycomb under x-direction uniaxial loading.（b）FBD of the structural unit cell under uniaxial loading.（c）Schematic of an anti-tetra-chiral honeycomb under x-y shearing load.（d）FBD of the structural unit cell under shearing load.

Note that as r goes to zero，the structure transforms into a regular square honeycomb.Upon substituting r=0 into Eqs.（C.1）-（C.3），we get Ex/Es=t/L，νxy=0，and Gxy/Es=0.5（t/L）3，whicharetheYoung’smodulus，Poisson’sratio，andshearmodulus of a regular square honeycomb，respectively.Employing the same procedure as outlined in the paper yields the principal directions for the two-dimensional compliance tensor of this honeycomb as kπ/4，where k is an integer.

Appendix D.Hierarchical diamond

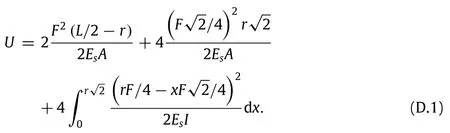
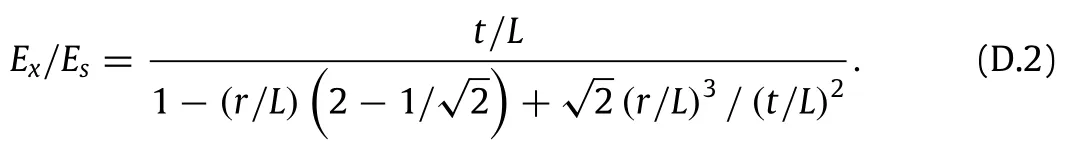
Next，inordertoobtainthePoisson’sratio，considerapairofvirtual forces acting on the unit cell in the lateral direction，as shown in Fig.D.1（c）.One fourth of the diamond is also shown in Fig.D.1（c）. Similar procedure is used to determine the unknown moments（M1and M2）acting on points 6 and 7.M1and M2are obtained as M1=-M2=rF/4-rP/4.Then，the strain energy of the unit cell is given as:

Fig.D.1.（a）Schematic of a hierarchical diamond honeycomb under x-direction uniaxial loading.（b）and（c）FBD of the structural unit cell under uniaxial loading，where P is a virtual force used for Poisson’s ratio calculations.（d）Schematic of a hierarchical diamond honeycomb under x-y shearing load.（e）FBD of the structural unit cell under shearing load.

Castigliano’s second theorem states that the total displacement of points 2 and 4 in the direction of virtual forces can be obtained using the relationSubstituting Eq.（D.3）into this equation gives.Then，using this equation， ϵy= δy/L gives the structure’s average strain in the y-direction due to the uniaxial loading，σx.The effective Poisson’s ratio of the structure is then defined as the negative of the ratio of the average strain in the y-direction，ϵyto the average strain in the x-direction，ϵxand obtained as the following:

Finally，todeterminetheshearmodulus，asshowninFig.D.1（d），we apply a uniform far-field shear stress，τxyto a typical hierarchical diamond honeycomb.FBD of the unit cell is also shown in Fig.D.1（e）.Likewise the previous section，there are only four equal shear forces acting on the unit cell’s external cut points，F，which can be obtained as a function of applying stress as，F=τxyL. Next，consider one fourth of the diamond as shown in Fig.D.1（e）. Components of unknown forces and moment acting on the externalcutpointsofthisportionoftheunitcellcanbedetermined asfunctionsofF，asshowninFig.D.1（e），whereM=F/2（L/2-r）. Hence，the strain energy of the unit cell is obtained as:

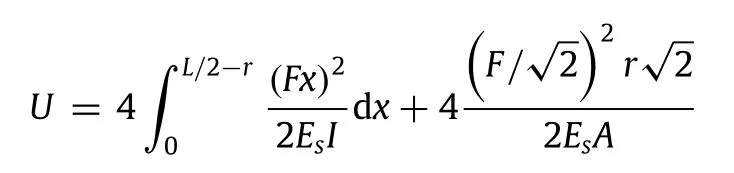
Then，（∂U/∂F）/L gives the total change of angle（i.e.，the shear strain，γxy）betweentwostraightlinesinitiallyparalleltothex-and y-axes.Finally，the effective shear modulus of the structure（Gxy，normalized with respect to the Young’s modulus of cell walls material）is defined as the ratio of the average shear stress，τxyto the average shear strain，γxyand obtained as the following:

Note that as r goes to zero，the structure transforms into a regular square honeycomb.Upon substituting r=0 into Eqs.（D.2），（D.4）and（D.6），we get Ex/Es=t/L，νxy=0，and Gxy/Es=0.5（t/L）3，whicharetheYoung’smodulus，Poisson’sratio，andshearmodulus of a regular square honeycomb，respectively.The principal directions for the two-dimensional compliance tensor of this structure areα=kπ/4，where k is an integer.

［1］S.Lubkin，Unidirectional waves on rings:Models for chiral preference of circumnutating plants，Bull.Math.Biol.56（1994）795-810.

［2］M.Oliverio，M.C.Digilio，P.Versacci，et al.，Shells and heart:Are human laterality and chirality of snails controlled by the same maternal genes？Am.J. Med.Genet.Part A 152A（2010）2419-2425.

［3］M.Schilthuizen，A.Davison，The convoluted evolution of snail chirality，Naturwissenschaften 92（2005）504-515.

［4］R.R.Sinden，DNA Structure and Function，Gulf Professional Publishing，1994.

［5］Z.L.Zhao，B.Li，X.Q.Feng，Hardedness-dependent hyperelasticity of biological soft fibers with multilayered helical structures，Int.J.Non-Linear Mech.81（2016）19-29.

［6］J.Aizenberg，J.C.Weaver，M.S.Thanawala，et al.，Skeleton of euplectella sp.: Structural hierarchy from the nanoscale to the macroscale，Science 309（2005）275-278.

［7］M.J.Buehler，Nature designs tough collagen:Explaining the nanostructure of collagen fibrils，Proc.Natl.Acad.Sci.103（2006）12285-12290.

［8］H.D.Espinosa，A.L.Juster，F.J.Latourte，et al.，Tablet-level origin of toughening in abalone shells and translation to synthetic composite materials，Nature Commun.2（2011）173.

［9］P.Fratzl，R.Weinkamer，Nature’s hierarchical materials，Prog.Mater.Sci.52（2007）1263-1334.

［10］L.J.Gibson，M.F.Ashby，B.A.Harley，Cellular Materials in Nature and Medicine，Cambridge University Press，2010.

［11］R.Lakes，Materials with structural hierarchy，Nature 361（1993）511-515.

［12］C.Ortiz，M.C.Boyce，Bioinspired structural materials，Science 319（2008）1053-1054.

［13］H.Qing，L.Mishnaevsky Jr.，3D hierarchical computational model of wood as a cellular material with fibril reinforced，heterogeneous multiple layers，Mech. Mater.41（2009）1034-1049.

［14］J.S.Wang，G.Wang，X.Q.Feng，et al.，Hierarchical chirality transfer in the growth of Towel Gourd tendrils，Sci.Rep.3（2013）03102.

［15］Z.L.Zhao，H.P.Zhao，J.S.Wang，etal.，Mechanicalpropertiesofcarbonnanotube ropes with hierarchical helical structures，J.Mech.Phys.Solids 71（2014）64-83.

［16］N.Fang，D.Xi，J.Xu，et al.，Ultrasonic metamaterials with negative modulus，Nat.Mater.5（2006）452-456.

［17］Z.Liu，X.Zhang，Y.Mao，et al.，Locally resonant sonic materials，Science 289（2000）1734-1736.

［18］R.Lakes，T.Lee，A.Bersie，et al.，Extreme damping in composite materials with negative-stiffness inclusions，Nature 410（2001）565-567.

［19］U.D.Larsen，O.Sigmund，S.Bouwstra，Design and fabrication of compliant micromechanisms and structures with negative Poisson’s ratio，in:Micro Electro Mechanical Systems，MEMS’96，Proceedings，An Investigation of Micro Structures，Sensors，Actuators，Machines and Systems，IEEE，The Ninth Annual International Workshop on，IEEE，1996，pp.365-371.

［20］R.Lakes，Foam structures with a negative Poisson’s ratio，Science 235（1987）1038-1040.

［21］E.Friis，R.Lakes，J.Park，Negative Poisson’s ratio polymeric and metallic foams，J.Mater.Sci.23（1988）4406-4414.

［22］C.Körner，Y.Liebold-Ribeiro，Asystematicapproachtoidentifycellularauxetic materials，Smart Mater.Struct.24（2015）025013.

［23］O.Sigmund，S.Torquato，Design of materials with extreme thermal expansion using a three-phase topology optimization method，J.Mech.Phys.Solids 45（1997）1037-1067.

［24］C.A.Steeves，S.L.Dos Santos E Lucato，M.He，et al.，Concepts for structurally robust materials that combine low thermal expansion with high stiffness，J. Mech.Phys.Solids 55（2007）1803-1822.

［25］O.Sigmund，S.Torquato，Composites with extremal thermal expansion coefficients，Appl.Phys.Lett.69（1996）3203-3205.

［26］F.Scarpa，Auxetic materials for bioprostheses［In the Spotlight］，IEEE Signal Process.Mag.25（2008）126-128.

［27］J.Choi，R.Lakes，Design of a fastener based on negative Poisson’s ratio foam，Cell.Polymers 10（1991）205-212.

［28］O.Sigmund，S.Torquato，I.A.Aksay，On the design of 1-3 piezocomposites using topology optimization，J.Mater.Res.13（1998）1038-1048.

［29］K.Evans，K.Alderson，Auxetic materials:the positive side of being negative，Eng.Sci.Educ.J 9（2000）148-154.

［30］F.Scarpa，G.Burriesci，F.Smith，et al.，Mechanical and electromagnetic behaviour of auxetic honeycomb structures，Aeronaut.J.107（2003）175.

［31］F.Scarpa，L.Ciffo，J.Yates，Dynamic properties of high structural integrity auxetic open cell foam，Smart Mater.Struct.13（2004）49.

［32］A.Spadoni，M.Ruzzene，Elasto-static micropolar behavior of a chiral auxetic lattice，J.Mech.Phys.Solids 60（2012）156-171.

［33］Y.Chen，F.Scarpa，Y.Liu，et al.，Elasticity of anti-tetrachiral anisotropic lattices，Int.J.Solids Struct.50（2013）996-1004.

［34］O.Levy，S.Krylov，I.Goldfarb，Design considerations for negative Poisson ratio structures under large deflection for MEMS applications，Smart Mater.Struct. 15（2006）1459.

［35］R.J.Jackman，S.T.Brittain，A.Adams，et al.，Design and fabrication of topologically complex，three-dimensional microstructures，Science 280（1998）2089-2091.

［36］G.Lesieutre，J.A.Browne，M.Frecker，Scaling of performance，weight，and actuation of a 2-D compliant cellular frame structure for a morphing wing，J.Intell.Mater.Syst.Struct.22（2011）979-986.

［37］K.R.Olympio，F.Gandhi，Flexible skins for morphing aircraft using cellular honeycomb cores，J.Intell.Mater.Syst.Struct.21（2010）1719-1735.

［38］E.A.Bubert，B.K.Woods，K.Lee，et al.，Design and fabrication of a passive 1D morphing aircraft skin，J.Intell.Mater.Syst.Struct.21（2010）1699-1717.

［39］A.Spadoni，M.Ruzzene，Static aeroelastic response of chiral-core airfoils，J.Intell.Mater.Syst.Struct.18（2007）1067-1075.

［40］H.Heo，J.Ju，D.-M.Kim，et al.，Passive morphing airfoil with honeycombs，in:Proceedings of the ASME International Mechanical Engineering Congress and Exposition，IMECE2011-64350，Denver，CO，2011.

［41］T.Johnson，M.Frecker，M.Abdalla，etal.，Nonlinearanalysisandoptimizationof diamond cell morphing wings，J.Intell.Mater.Syst.Struct.20（2009）815-824.

［42］D.Bornengo，F.Scarpa，C.Remillat，Evaluation of hexagonal chiral structure for morphing airfoil concept，Proc.Inst.Mech.Eng.G 219（2005）185-192.

［43］J.L.Reed Jr.，C.D.Hemmelgarn，B.M.Pelley，et al.，Adaptive wing structures，in: Proc.of SPIE Vol，2005，pp.133.

［44］J.Ju，D.-M.Kim，K.Kim，Flexible cellular solid spokes of a non-pneumatic tire，Compos.Struct.94（2012）2285-2295.

［45］J.Ju，B.Ananthasayanam，J.D.Summers，P.Joseph，Design of cellular shear bands of a non-pneumatic tire-investigation of contact pressure，SAE Int.J. Passenger Cars Mech.Syst.3（2010）598-606.

［46］A.Alderson，K.Alderson，D.Attard，et al.，Elastic constants of 3-，4-and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading，Compos.Sci.Technol.70（2010）1042-1048.

［47］A.Alderson，K.L.Alderson，G.Chirima，et al.，The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinderligament honeycombs，Compos.Sci.Technol.70（2010）1034-1041.

［48］D.Prall，R.Lakes，Properties of a chiral honeycomb with a Poisson’s ratio of—1，Int.J.Mech.Sci 39（1997）305-314.

［49］Y.Chen，X.Liu，G.Hu，etal.，Micropolarcontinuummodellingofbi-dimensional tetrachiral lattices，Proc.R.Soc.A 470（2014）20130734.

［50］Y.Chen，X.Liu，G.Hu，Micropolar modeling of planar orthotropic rectangular chiral lattices，Comptes Rendus Mécanique 342（2014）273-283.

［51］A.Bacigalupo，L.Gambarotta，Homogenizationofperiodichexa-andtetrachiral cellular solids，Compos.Struct.116（2014）461-476.

［52］A.Ajdari，B.H.Jahromi，J.Papadopoulos，et al.，Hierarchical honeycombs with tailorable properties，Int.J.Solids Struct.49（2012）1413-1419.

［53］R.Oftadeh，B.Haghpanah，J.Papadopoulos，et al.，Mechanics of anisotropic hierarchical honeycombs，Int.J.Mech.Sci.81（2014）126-136.

［54］R.Oftadeh，B.Haghpanah，D.Vella，et al.，Optimal fractal-like hierarchical honeycombs，Phys.Rev.Lett.113（2014）104301.

［55］F.Barthelat，H.Espinosa，An experimental investigation of deformation and fracture of nacre-mother of pearl，Exp.Mech.47（2007）311-324.

［56］N.M.Pugno，Mimicking nacre with super-nanotubes for producing optimized super-composites，Nanotechnology 17（2006）5480.

［57］Z.Zhang，Y.-W.Zhang，H.Gao，On optimal hierarchy of load-bearing biological materials，Proc.R.Soc.Lond.Biol.278（2011）519-525.

［58］D.Mousanezhad，H.Ebrahimi，B.Haghpanah，et al.，Spiderweb honeycombs，Int.J.Solids Struct.66（2015）218-227.

［59］D.Rayneau-Kirkhope，Y.Mao，R.Farr，Ultralight fractal structures from hollow tubes，Phys.Rev.Lett.109（2012）204301.

［60］B.Haghpanah，J.Papadopoulos，A.Vaziri，Plastic collapse of lattice structures under a general stress state，Mech.Mater.68（2014）267-274.

［61］B.Haghpanah，J.Papadopoulos，D.Mousanezhad，et al.，Buckling of regular，chiral and hierarchical honeycombs under a general macroscopic stress state，Proc.R.Soc.A 470（2014）20130856.

［62］Y.Sun，N.Pugno，Hierarchical fibers with a negative Poisson’s ratio for tougher composites，Materials 6（2013）699-712.

［63］F.Song，J.Zhou，X.Xu，et al.，Effect of a negative Poisson ratio in the tension of ceramics，Phys.Rev.Lett.100（2008）245502.

［64］R.Lakes，High damping composite materials:effect of structural hierarchy，J.Compos.Mater.36（2002）287-297.

［65］D.Mousanezhad，S.Babaee，H.Ebrahimi，et al.，Hierarchical honeycomb auxetic metamaterials，Sci.Rep.5（2015）18306.

［66］D.Mousanezhad，S.Babaee，R.Ghosh，etal.，Honeycombphononiccrystalswith self-similar hierarchy，Phys.Rev.B 92（2015）104304.

［67］R.S.Farr，Fractal design for an efficient shell strut under gentle compressive loading，Phys.Rev.E 76（2007）056608.

［68］R.S.Farr，Fractal design for efficient brittle plates under gentle pressure loading，Phys.Rev.E 76（2007）046601.

［69］D.Rayneau-Kirkhope，R.Farr，Y.Mao，Fractal-like dependence in the designs of efficient pressure-bearing structures，Europhys.Lett.93（2011）34002.

［70］D.Rayneau-Kirkhope，Y.Mao，R.Farr，et al.，Hierarchical space frames for high mechanical efficiency:Fabrication and mechanical testing，Mech.Res. Commun.46（2012）41-46.

［71］B.Haghpanah，R.Oftadeh，J.Papadopoulos，et al.，Self-similar hierarchical honeycombs，Proc.R.Soc.A 469（2013）20130022.

［72］A.P.Boresi，R.J.Schmidt，Advanced Mechanics of Materials，Wiley，2003.

［73］R.Christensen，Sufficient symmetry conditions for isotropy of the elastic moduli tensor，J.Appl.Mech.54（1987）772.

［74］L.J.Gibson，M.F.Ashby，Cellular Solids:Structure and Properties，Cambridge Univ.Pr.，1999.

［75］C.T.Herakovich，Mechanics of Fibrous Composites，first ed.，Wiley，1997.

［76］H.Harders，K.Hupfer，J.Rösler，Influence of cell wall shape and density on the mechanical behaviour of 2D foam structures，Acta Mater.53（2005）1335-1345.

12 January 2016

.

E-mail address:vaziri@coe.neu.edu（A.Vaziri）.

http://dx.doi.org/10.1016/j.taml.2016.02.004

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

in revised form

*This article belongs to the Solid Mechanics