Analytical design of effective thermal conductivity for fluid-saturated prismatic cellular metal honeycombs

Wenbin Wng，Xiohu Yng，b，Bin Hn，c，Qincheng Zhng，d，∗，Xingfei Wng，Tinjin Lu，d，∗

aMOE Key Laboratory for Multifunctional Materials and Structures，Xi’an Jiaotong University，Xi’an 710049，China

bDepartment of Building Environment and Energy Engineering，Xi’an Jiaotong University，Xi’an 710049，China

cSchool of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，China

dState Key Laboratory for Strength and Vibration of Mechanical Structures，Xi’an Jiaotong University，Xi’an 710049，China

Analytical design of effective thermal conductivity for fluid-saturated prismatic cellular metal honeycombs

Wenbin Wanga，Xiaohu Yanga，b，Bin Hana，c，Qiancheng Zhanga，d，∗，Xiangfei Wanga，Tianjian Lua，d，∗

aMOE Key Laboratory for Multifunctional Materials and Structures，Xi’an Jiaotong University，Xi’an 710049，China

bDepartment of Building Environment and Energy Engineering，Xi’an Jiaotong University，Xi’an 710049，China

cSchool of Mechanical Engineering，Xi’an Jiaotong University，Xi’an 710049，China

dState Key Laboratory for Strength and Vibration of Mechanical Structures，Xi’an Jiaotong University，Xi’an 710049，China

H i G H L i G H T s

•Modeled effective thermal conductivity（ETC）of prismatic cellular metal honeycombs（PCMHs）with a wider porosity range（0.7～0.98）.

•Proposed ligament thermal conduction efficiency（LTCE）to analyze the influence of ligament inclined angle.

•Utilized equivalent interaction angle（EIA）to assess the overall heat conduction ability of honeycombs.

•Optimized the design for either heat conduction or insulation applications.

A R T i C L Ei N F O

Article history:

14 January 2016

Accepted 19 January 2016

Available online 20 February 2016

Effective thermal conductivity

Prismatic cellular metal honeycomb

Ligament heat conduction efficiency

Analytical design

Equivalent interaction angle

A comparative optimal design of fluid-saturated prismatic cellular metal honeycombs（PCMHs）having different cell shapes is presented for thermal management applications.Based on the periodic topology of each PCMH，a unit cell（UC）for thermal transport analysis was selected to calculate its effective thermal conductivity.Without introducing any empirical coefficient，we modified and extended the analytical model of parallel-series thermal-electric network to a wider porosity range（0.7～0.98）by considering the effects of two-dimensional local heat conduction in solid ligaments inside each UC.Good agreement was achieved between analytical predictions and numerical simulations based on the method of finite volume.The concept of ligament heat conduction efficiency（LTCE）was proposed to physically explain the mechanisms underlying the effects of ligament configuration on effective thermal conductivity（ETC）. Based upon the proposed theory，a construct strategy was developed for designing the ETC by altering the equivalent interaction angle with the direction of heat flow:relatively small average interaction angle for thermal conduction and relatively large one for thermal insulation.

©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http:// creativecommons.org/licenses/by-nc-nd/4.0/）.

Prismatic cellular metal honeycombs（PCMHs），as one kind of multifunctional lattice frame materials（LFMs），are of considerable interest in practical applications for their excellent performance in load bearing，acoustic/vibration damping，and thermal management［1-3］.Generally，an interconnected network of solid struts and plates，as PCMH edges and faces，is integrated inside which a number of periodic prismatic voids arranged in one particular direction are formed.Through topological design of cell size and distributions，distinct cellular architectures as shown in Fig.1 may be constructed.Not only high specific stiffness/strength［4］，but also multifunctional designs can be achieved with such PCMHs. For instance，in situations where a structure needs to carry simultaneously mechanical and thermal loads［5-8］，PCMHs can be employed for active cooling applications such as multi-chip cooling（Fig.1（o））and jet blast deflecting［3］.Alternatively，when the forced convective flow is stagnant［9，10］，PCMHs may act as thermal insulation in thermal protection designs，e.g.，the skin layer of a re-entry vehicle.For these applications，it is essential to achieve distinctive target thermal function，either heat dissipation or insulation，via topological design.

For heat dissipation/insulation applications，the effective thermal conductivity（ETC）of PCMH is a key material property.To estimate the ETC of PCMH saturated with different kinds of fluids（e.g.，air，water，or refrigerant），it is unlikely to employ conventional analytical approaches based on idealized assumptions，such as random homogenization［11］and phase symmetrical distribution［12］，to obtain satisfactory predictions due to the complicated and heterogeneous topology of PCMH.Rather，resistance analysis of thermal-electrical networks shows flexible applicability，which has been recently applied to analyze thermal transport in a variety of porous materials，including open-or closed-cell foams［12-15］，sintered metal fiber networks［16］and honeycombs［10，17］.For example，based on the idealized non-twisted geometric model for wire-woven bulk Kagome（WBK）structures，Yang et al.［12］developed an analytical ETC model based on one-dimensional（1D）conduction for high porosity（＞0.9）air-saturated WBK sandwiches，and empirically correlated the anisotropic ETC behavior of WBK using numerical simulations.However，few studies have been conducted either on ETC prediction for a wide range of PCMHs or thermal design of PCMHs having different functionalities.Besides，as most LFMs（including the PCMHs considered here）exhibit anisotropic topologies and a wide range of porosity，existing ETC models for porous media need to be revisited.Further，there is insufficient physical insight into thermal transport in such materials as well as the mechanisms of pore-level heat transport.

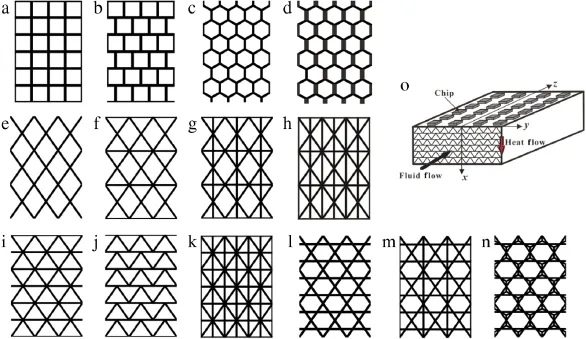
Fig.1.Cross-sectional view of PCHMs with different cell shapes:（a）square honeycomb-I；（b）square honeycomb-II；（c）uniform hexagonal honeycomb；（d）non-uniform hexagonal honeycomb；（e）diamond honeycomb-I；（f）diamond honeycomb-II；（g）diamond honeycomb-III；（h）diamond honeycomb-IV；（i）triangular honeycomb；（j）multilayered corrugations；（k）mixed triangular-square honeycomb；（l）Kagome-I；（m）Kagome-II；（n）Kagome-III；（o）schematic of multi-layered corrugated core heat exchanger for multi-chip cooling application.

This study aims to calculate the ETCs of fourteen different types of fluid-saturated PCMH using a combined approach of analytical modeling and numerical simulation.The PCMHs are divided into layers so that the parallel model can be applied to explore the detailed mechanisms of solid-fluid heat exchange in each layer.Subsequently，to capture local two-dimensional（2D）heat conduction，these layers are treated with the series model using a simplistic approximate method.Further，to physically explain the mechanisms underlying the effect of ligament configuration on ETC，the concept of ligament heat conduction efficiency is proposed.

With reference to Fig.2（a），consider a porous medium（e.g.，multi-layer corrugated panel）with periodical ligaments immergedinalowconductingfluidphase.Becauseofsymmetry，only one half of a whole corrugated cell is selected.The conventional series model of thermal-electric resistance model［18］takes theform of

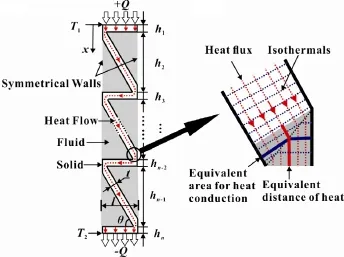
Fig.2.（a）Schematic of heat conduction process in multi-layer corrugated panel and（b）approximate model for 2D local heat conduction.θis inclination angle.

where kedenotes the ETC of PCMH，and ke，1，ke，2，...，ke，nare the ETC of each layer（hi）which can be calculated using the parallel model of thermal-electric resistance，as

Here，ksandkfarethethermalconductivitiesofsolidligamentsand saturating fluid，respectively；Vi，sand Viare the ligament-occupied volume and the volume of the total layer，respectively.

BeforetakingfurtheractiontodeveloptheanalyticalETCmodel for PCMHs，the principle task is to determine the thermo-physical mechanisms underlying heat flow in both fluid and solid media. In general，depending upon the ratio of solid conductivity to fluid conductivity，there mainly exist three different mechanisms:（a）when ks≫ kf，heat conduction in solid flows along the solidligaments，while it flows perpendicular to the heating and cooling surfaces in fluid；（b）when ksand kfare comparable，heat flow is homogenized in the PCMH；（c）when ks≪ kf，heat flow in fluid becomes dominant，flowing approximately perpendicular to solid ligaments.Therefore，for porous metallic materials such as PCMHs，the thermal conductivity of solid ligaments is significantly larger than that of the saturating fluid，e.g.，ks/kf＞ 8000 and ks/kf＞300 for air-and water-saturated aluminum PCMHs，respectively. As a result，heat flow in such PCMHs is mainly transported along the tortuous aluminum ligaments.Consequently，according to the Fourier law of heat conduction，a modified ETC for each layer of the PCMH is given by

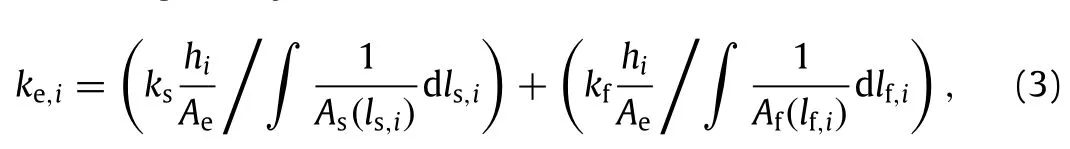
Based on the theory as outlined above，further analysis is needed to account for different cell distributions.As shown in Fig.2（a）for multi-layer corrugation，with the face sheet selected as layer 1，the direction of heat flow is perpendicular to it since constant temperature is imposed，and ke，1is equal to ksin this layer.In layer 2，heat mainly flows along the solid ligaments，but at the joint that connects different ligaments，local 2D conduction exists due to sudden change in heat conduction area.The effect of local2DconductionisnotsignificantforhighporosityPCMHs（ε＞0.9）.However，for lower porosity levels（0.7～0.9），the 2D effect on ETC is no longer negligible because the 2D effect increases with increasing joint section volume as the porosity is reduced.Because of the intrinsic complexity of calculating analytically the 2D effect，a numerical method can be utilized to decide the integration of heat conduction distance［19］.To this end，a series of numerical simulations are carried out to estimate the integral mean thermal path through the‘corner’（local 2D conduction area）.It is found that the equivalent heat conduction area and distance may be approximately determined by the middle line of the cross-section at the corner，e.g.，isothermals and heat flux of specific triangular case as illustrated in Fig.2（b）.Therefore，the ETC of layer 2 may be expressed as

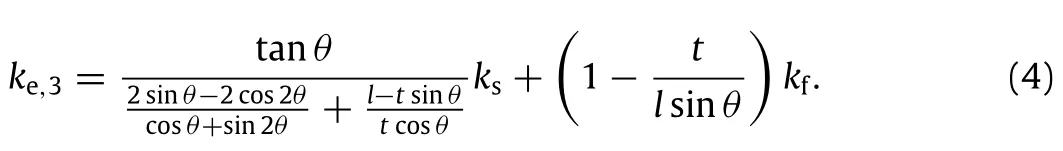
In the third layer，because of its unique topology and the big differenceofETCbetweensolidandfluid，heatflowsperpendicular to the x-direction.Based on such characteristics of heat flow，ETC in this layer may be determined as

Similarly，the rest of layers can all be treated.Substituting the ETCs of these layers into Eq.（1）gives the final prediction of ETC for a multi-layer corrugated panel.

Next，to determine an optimal topology with high/low thermal conductivity along the x-direction of Fig.1，fourteen PCMHs with different distributions of cell shape and cell size are analyzed. These PCMHs may be fabricated using a variety of methods，such as assembling slotted sheets，bonding corrugated plates，direct extrusion，and thermal chemical processing［20-22］.In the method of slotted sheets assembling，electro-discharge machining（EDM）is firstly applied to slot thin metal strips，which are thenglued or brazed together.Honeycombs with flat edges，such as square honeycomb and diamond structures，can be fabricated by this method.However，panels with bent edges like corrugated panels are typically processed by preparing corrugated plates first，followed by stacking these plates to form multi-layer structures. The extrusion and thermal chemical methods are usually utilized to process PCMHs in a single step.In Fig.1，the prismatic cellular materials all possess cell ligaments with uniform thickness except for the square honeycomb in Fig.1（d）that has two double thickness walls.Detailed expressions of ETC prediction for PCMHs are listed in Table 1.

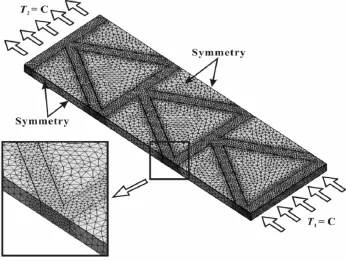
Fig.3.Boundary conditions and mesh details for multi-layer corrugated panel.

To validate the analytical model and to further explore the physical process of heat transport in prismatic cellular materials，numerical simulations are carried out using the finite volume method（FVM）embedded into the commercially available software ANSYS-Fluent 14.5.Solid geometries for different PCMHs generated with SolidWorks are first meshed in ANSYS-ICEM 14.5 and then exported to ANSYS-Fluent 14.5 for steady-state heat conduction analysis.For illustration，Fig.3 depicts the boundary conditions and mesh details for a multi-layer corrugated panel. Constant temperature boundary conditions are applied on the upper and lower faces，while the other four faces are taken as symmetrical.

Before proceeding further，a validation process is conducted. The ETCs of uniform hexagonal and triangular honeycombs are analytically modeled and numerically simulated，respectively.A comparison is made between the present predictions and the published numerical data［23］.It is established that the present numerical analysis can not only reproduce existing simulation results（with a maximum deviation within 3.0%）but also achieve good agreement with the analytical predictions.

Subsequently，analytical and numerical analyses are performed for the architectures shown in Fig.1 to explore the physical mechanismsofheatconductionindifferentPCMHs.Porosity，atthe first place，is considered to be a key factor in determining the ETC. Relatively high porosities in the range of 0.7～0.98 are considered，since the PCMHs within this porosity range have been extensively investigated for their high specific stiffness and strength.

For square-I，square-II，uniform and non-uniform hexagon honeycombs，once porosity is determined，cell distribution is correspondingly decided.However，for the remaining PCMH structures of Fig.1，porosity is related to inclination angle of ligaments and ligament aspect ratio（t/l）.To preclude the influence of inclination angle and to address specifically the effect of porosity，all the inclination angles are fixed at 60°.It can be observed from Fig.4 that，for all the structures considered，the ETC in either x-or y-direction increases with decreasing porosity.It needs to be pointed out thatthe ETCs are not linearly correlated with porosity.For sufficiently high porosities（ε＞0.9），previous investigations［10，17］showed that the ETC exhibits a linear relationship with porosity，for heat conduction in thin solid ligaments could be approximately treated as 1D conduction.As the porosity is reduced，however，2D conduction in solid ligaments becomes remarkable.For instance，when the porosity is reduced to～0.7，ignoring such 2D heat conduction brings～20%deviation in ETC prediction.The effect of 2D heat con-duction on ETC prediction has been accounted for by the present model.Dividing a PCMH structure into sub-layers enables accurate depiction of heat conduction in each layer and efficient consideration of thermal interaction between fluid and solid.Besides，the concept of equivalent heat conduction distance and area proposedinthepresentstudyaccountsforlocalthermalconductionin solid，hence achieving a more accurate prediction（less than 4.6%）in comparison with the conventional 1D model.

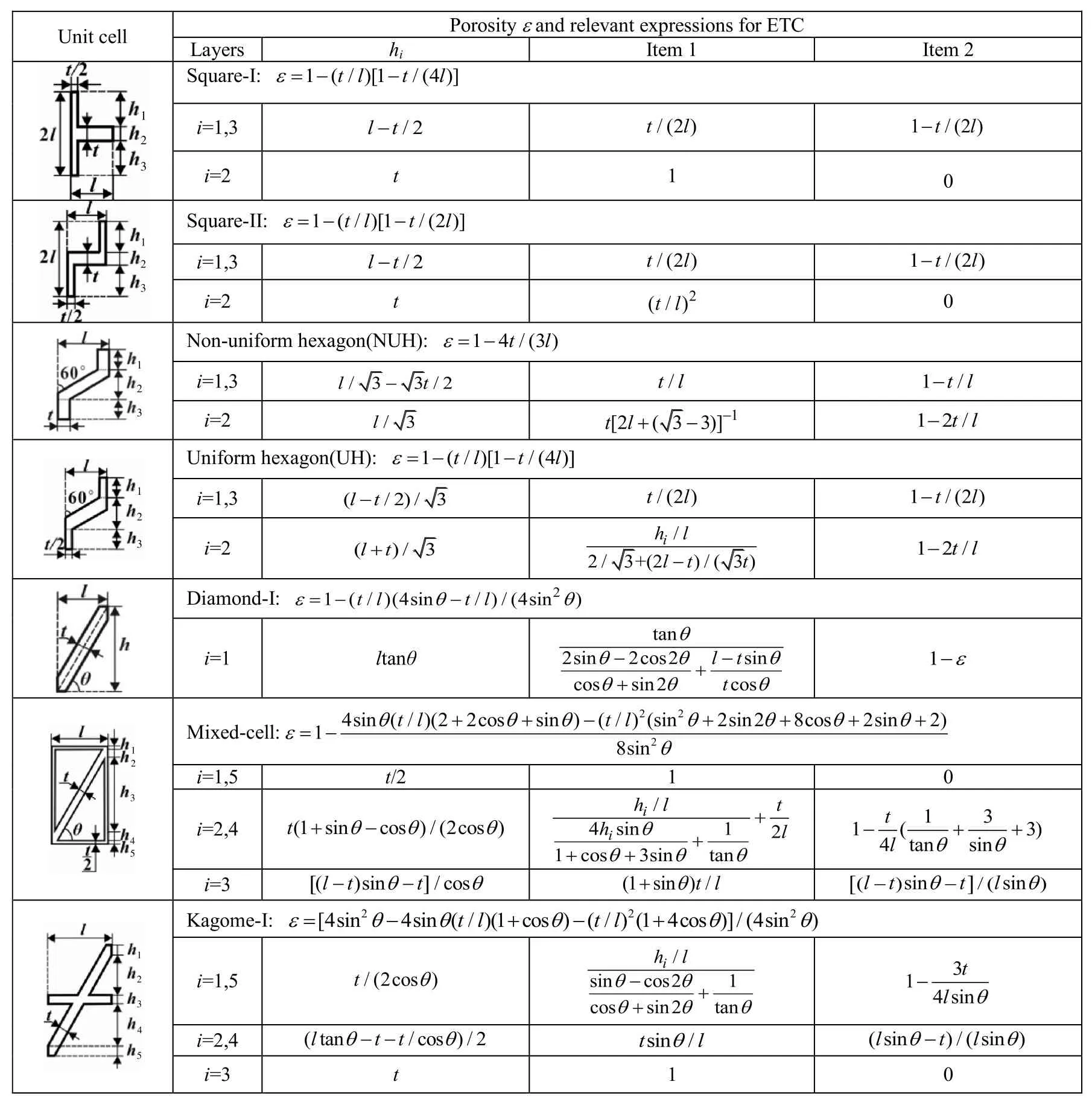
Table 1 Porosity（ε）and relevant items in Eqs.（1）and（3）for ETC along x-direction of selected PCMHs.

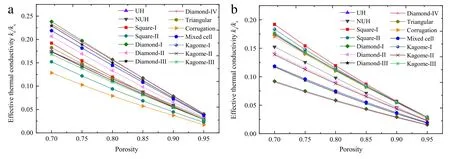
Fig.4.Analytical predictions of ETCs for selected honeycombs in:（a）x-direction；（b）y-direction.

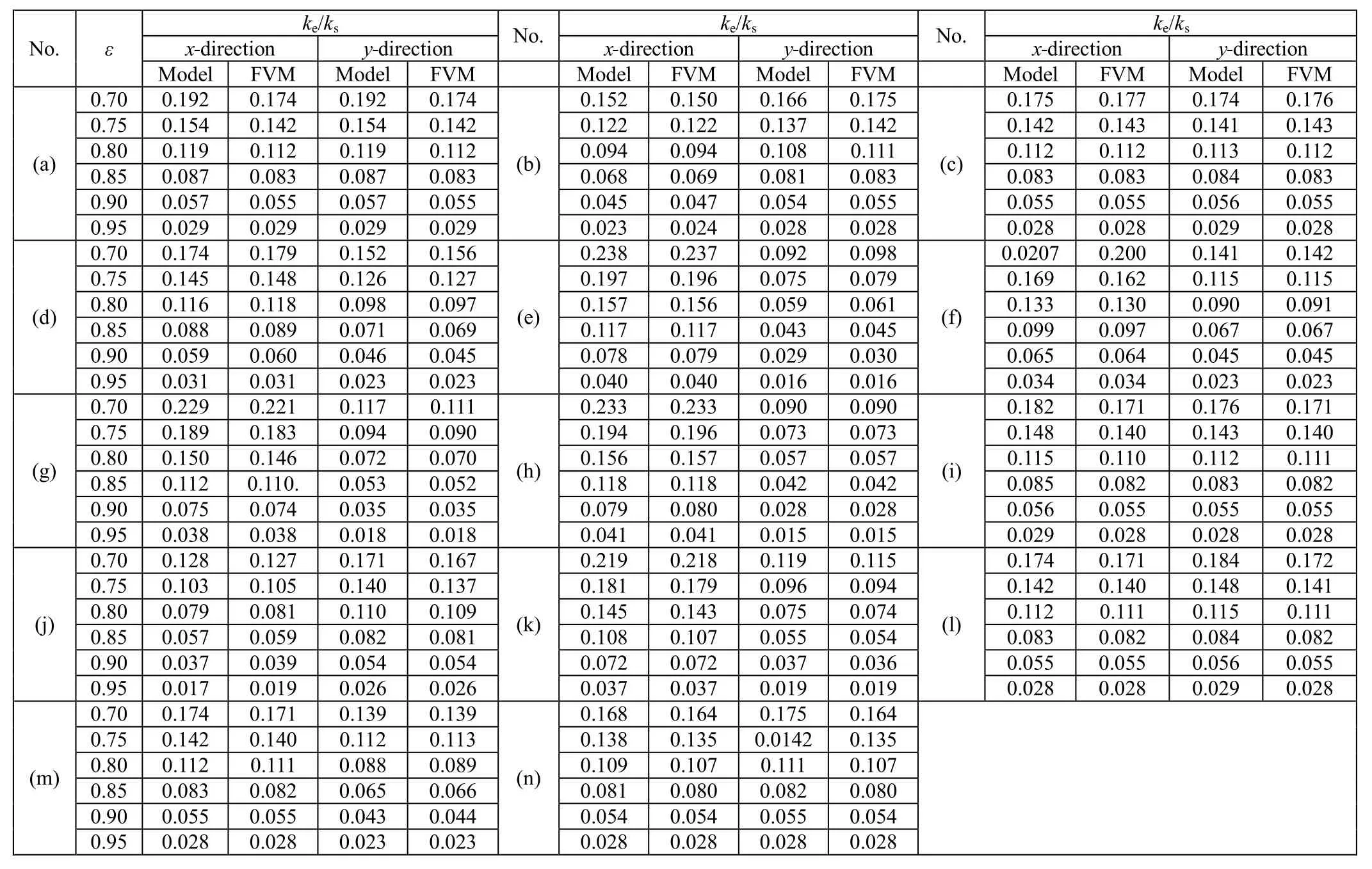
Table 2 Analytical and numerical predictions of ETC in x-and y-directions for PCMHs of Fig.1.

To design a porous material/structure for practical applications，the aspect ratio and inclination angle of ligaments as well as cell shape are the key morphological parameters to be considered. For thermal management with high ETC，the main principle is to put effective materials（metals）along the heat flux direction.In a lattice truss structure，the cell ligaments may be categorized into three maintypes:parallel，perpendicular，and inclinedto heat flow direction with an intersection angle of（90°-θ）.If the ligaments are placed perpendicular to heat flow direction，they compose a series system together with the surrounding fluid，of which the ETC may be expressed as 1/ke= εs/ks+εf/kf.In comparison，if the ligaments are parallel to heat flow，a parallel model may be utilized to predict the ETC，as ke=εsks+εfkf.The parallel system provides a heat path in solid with maximum heat conduction area and shortest heat transfer distance.With increasing rotation of the ligaments from the parallel system，the distance for heat conduction increases while the heat conduction area decreases，until a series system is formed.According to Fourier’s law，we may have two arguments for a certain metallic ligament saturated in fluid.The superior thermal path for a single ligament is parallel to heat flux（parallel model for highest ETC），which possesses the highestthermalconductionefficiency，yieldingtheupperboundof ETC.On the contrary，if the ligament is perpendicular to heat flow（seriesmodelforlowestETC），ithasthelowestthermal conduction efficiency，resulting in the lower bound of ETC.

From the results of Fig.4 and Table 2 it can be seen that，for a fixed inclination angle of 60°for all the PCMHs，the diamond-I of Fig.1（e）provides superior thermal conduction，while the multilayer corrugation of Fig.1（j）provides superior thermal insulation. For PCMHs having identical inclination angle，all the ligaments in diamond-I are configured with an intersection angle of 30° to heat flow:that is，no ligament is placed normal to heat flow. Consequently，diamond-IhasthehighestETCamongallthePCMHs investigated；see Fig.4（a）and Table 2.In diamond-II，some of its ligaments are placed normal to heat flow，leading to a reduced ETC along the x-direction compared with its parent structure，i.e.，diamond-I.In diamond-III and diamond-IV，as a few parallel ligaments are placed along the heat conduction direction，their ETCs are higher than that of diamond-II.

Based on the physical mechanism of heat conduction，it is worthy to understand the particularly low ETC of multilayer corrugation.Given the distinct difference between fluid and metal as well as the special design of the joint，heat in this structure is forced to conduct along not only the inclined ligaments but also the‘series’ligaments，increasing dramatically the heat conduction distance.Compared to triangular structures as well as other competing honeycombs，the significant increase of heat conduction distance in the multi-layer corrugation reduces considerably its ETC.

To further reveal the physical mechanisms，the concept of ligament thermal conduction efficiency（LTCE）is proposed to explain the reason why PCMHs with identical porosity exhibit different ETCs，as shown in Fig.4 and Table 2.Quantitatively，LTCE is defined here asη=sin2θe，θebeing the equivalent interaction angle（EIA）of a whole UC，which may be calculated by solving equation ke= （sin2θe）εsks+（1-εs）kfafter obtaining the ETC of a PCMH using the present analytical model.For diamond-I withθfixedat60°，thereexistsonlyonekindofligaments，i.e.，ligaments with an inclination angle of 60°.However，its EIA（θe）along the xdirection is calculated to be 59.2°.This is understandable because，at the joint，heat conduction area in the solid is reduced and hence the thermal conduction ability is decreased，which is reflected as a decrease in EIA.Thus，the presence of joints leads to reduced LTCE in PCMHs.

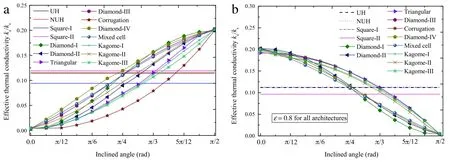
Fig.5.Influence of ligament inclination angle（θin Fig.2）on ETC of selected honeycombs:（a）x-direction；（b）y-direction.

Table 3 Influence of ligament inclination angle on EIA of triangular honeycomb with a porosity of 0.8.

Relative to diamond-I，other PCMHs have more complicated cellular topologies.In these PCMHs，a variety of ligaments with different inclination angles exist，forming a competing system that finally determines the ETC.Figure 5 presents the effect of ligament inclination angle upon ETC for PCMHs having identical porosity（0.8）.Except those PCMHs having fixed inclination angle（square-I，square-II，uniform hexagon and non-uniform hexagon honeycombs），the ETC along the x-direction increases withincreasinginclinationangle（θinFig.2）.Forafixedinclination angle（albeit less than 45°），square-II is the most favorable PCMH for heat conduction.Otherwise，diamond-I or diamond-IV is the preferable choice.

We have explained in previous sections the difference of ETC between different PCMHs.In this section，we demonstrate further that，as the inclination angle is increased，the ETC increases.The physical mechanism for this change is that there is more heat conduction material in a parallel system increases，whereas less metallic material is present in its counterpart series system.As previously discussed，placing more materials in a series system（i.e.，perpendicular to the heating surfaces）is beneficial for heat conduction，resulting in increased ETC.Based on the present theory for ligament heat conduction efficiency，the variation trend of ETC in the y-direction as a function of inclination angle（Fig.5（b））may be understood as well.Besides，Table 3 presents the EIA of triangular honeycomb for selected inclination angles. As the inclination angle is increased，the EIA increases along the x-direction but decreases along the y-direction.Therefore，for those PCMHs with angle flexibility，increasing the inclination angle enhances conductivity along the x-direction and reduces conductivity along the y-direction.

In summary，the effective thermal conductivities of fourteen different types of prismatic cellular metal honeycomb saturated with fluid are calculated，both numerically and analytically.A parallel-series thermal-electric network model based on unit cell topology is developed.The model is verified within a wide porosity range（0.7～0.98）by considering local 2D heat conduction and interactive effect between fluid and solid.The model is then utilized to analyze and design thermal conduction/insulation honeycomb structures.For thermal conduction，the fundamental principle is to place more metals along the heat flux direction. For thermal insulation，the multilayered corrugation is preferable because its unique structure enables elongated heat conduction distance.For a given cellular topology，the LTCE may serve as a quantitative parameter to identify competing mechanisms of heat conductionindifferenttypesofcellligament.WithlargeLTCEs，the overall competing effect of cell ligaments enhances the conduction ability of a honeycomb；otherwise，the structure is favorable for thermal insulation.

Acknowledgments

This work was supported by the National Natural Science Foundation of China（51506160，11472208，11472209），China Post-Doctoral Science Foundation Project（2015M580845），the FundamentalResearchFundsforXi’anJiaotongUniversity（xjj2015102），and the Beijing Key Lab of Heating，Gas Supply，Ventilating and Air Conditioning Engineering（NR2016K01）.

［1］Q.C.Zhang，X.H.Yang，P.Li，et al.，Bioinspired engineering of honeycomb structure—using nature to inspire human innovation，Prog.Mater.Sci.74（2015）332-400.

［2］A.G.Evans，J.W.Hutchinson，N.A.Fleck，et al.，The topological design of multifunctional cellular metals，Prog.Mater.Sci.46（2001）309-327.

［3］T.J.Lu，D.P.He，C.Q.Chen，et al.，The multi-functionality of ultra-light porous metals and their applications，Adv.Mech.36（2006）517-535（in Chinese）.

［4］L.J.Gibson，M.F.Ashby，Cellular Solids:Structure and Properties，Cambridge University Press，1997.

［5］C.C.Seepersad，B.Dempsey，J.K.Allen，et al.，Design of multifunctional honeycomb materials，AIAA J.42（2004）1025-1033.

［6］C.C.Seepersad，R.S.Kumar，J.K.Allen，et al.，Multifunctional design of prismatic cellular materials，J.Comput-Aided.Mater.11（2004）163-181.

［7］D.F.Wu，A.F.Zhou，L.M.Zheng，et al.，Study on the thermal protection performance of superalloy honeycomb panels in high-speed thermal shock environments，Theor.Appl.Mech.Lett.4（2014）021004.

［8］S.T.Liu，Y.C.Zhang，L.Peng，New analytical model for heat transfer efficiency of metallic honeycomb structures，Int.J.Heat Mass Transfer 51（2008）6254-6258.

［9］C.T.Hsu，P.Cheng，K.W.Wong，Modified Zehner-Schlunder models for stagnant thermal conductivity of porous media，Int.J.Heat Mass Transfer 37（1994）2751-2759.

［10］T.J.Lu，Heat transfer efficiency of metal honeycombs，Int.J.Heat Mass Transfer 42（1999）2031-2040.

［11］T.H.Bauer，A general analytical approach toward the thermal conductivity of porous media，Int.J.Heat Mass Transfer 36（1993）4181-4191.

［12］X.H.Yang，J.X.Bai，J.J.Kang，etal.，Effectivethermalconductivityofwire-woven bulk Kagome sandwich panels，Theor.Appl.Mech.Lett.4（2014）051010.

［13］X.H.Yang，J.J.Kuang，T.J.Lu，et al.，A simplistic analytical unit cell based model for the effective thermal conductivity of high porosity open-cell metal foams，J.Phys.D Appl.Phys.46（2013）255302-255307.

［14］X.H.Yang，T.J.Lu，T.Kim，Effective thermal conductivity modelling for closedcell porous media with analytical shape factors，Transp.Porous Media 100（2013）211-224.

［15］X.H.Yang，J.X.Bai，H.B.Yan，et al.，An analytical unit cell model for the effective thermal conductivity of high porosity open-cell metal foams，Transp.Porous Media 102（2014）403-426.

［16］Z.G.Qu，T.S.Wang，W.Q.Tao，et al.，A theoretical octet-truss lattice unit cell model for effective thermal conductivity of consolidated porous materials saturated with fluid，Heat Mass Transfer 48（2012）1385-1395.

［17］S.Gu，T.J.Lu，A.G.Evans，On the design of two-dimensional cellular metals for combined heat dissipation and structural load capacity，Int.J.Heat Mass Transfer 44（2001）2163-2175.

［18］J.C.Maxwell，ATreatiseonElectricityandMagnetism，ClarendonPress，Oxford，1881.

［19］X.H.Yang，T.J.Lu，T.Kim，Thermal stretching in two-phase porous media: Physical basis for Maxwell model，Theor.Appl.Mech.Lett.3（2013）57-61.

［20］H.N.Wadley，Multifunctional periodic cellular metals，Philos.T.R.Soc.A 364（2006）31-68.

［21］J.K.Cochran，K.J.Lee，D.L.McDowell，et al.Multifunctional metallic honeycombs by thermal chemical processing，in:Proceedings of Processing and Properties of Lightweight Cellular Metals and Structures，2002，pp.127-136.

［22］F.Côté，V.S.Deshpande，N.A.Fleck，et al.，The out-of-plane compressive behavior of metallic honeycombs，Mater.Sci.Eng.A 380（2004）272-280.

［23］S.Hyun，S.Torquato，Optimal and manufacturable two-dimensional，Kagomelike cellular solids，J.Mater.Res.17（2002）137-144.

29 September 2015

at:MOE Key Laboratory for Multifunctional Materials and Structures，Xi’an Jiaotong University，Xi’an 710049，China.

E-mail addresses:zqc111999@xjtu.edu.cn（Q.Zhang），tjlu@xjtu.edu.cn（T.Lu）.

http://dx.doi.org/10.1016/j.taml.2016.01.003

2095-0349/©2016 The Authors.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

in revised form

*This article belongs to the Solid Mechanics