基于网格单元和P权值的离群数据挖掘方法
2016-11-14冯婷婷张继福
冯婷婷,张继福
(太原科技大学 计算机科学与技术学院,太原 030024)
基于网格单元和P权值的离群数据挖掘方法
冯婷婷,张继福
(太原科技大学 计算机科学与技术学院,太原 030024)
基于单元的离群数据挖掘是一类典型的离群数据挖掘方法,尽管具有可以快速识别离群数据和修剪非离群数据等优点,但由于只从单元的角度修剪非离群数据,可能使一些单元无法准确的确定离群数据。给出了一种基于网格单元和P权值的离群数据挖掘算法。该算法首先将数据集的每维均分,划分网格单元,并在网格单元中,筛选出离群数据和正常数据网格单元;对既含有离群数据又有正常数据的网格单元,采用P权值的方法,来度量和确定离群数据,从而进一步提高了离群挖掘精度;最后,采用UCI数据集,实验验证了该算法的有效性和可行性。
数据挖掘;离群数据;网格单元;P权值;距离
离群数据挖掘是数据挖掘的一个重要分支,离群数据就是一个数据对象,显著不同于其他数据对象,好像是被不同的机制产生的一样[1],并已经应用在信用卡欺诈检测[2],网络入侵检测[3-4],环境检测[5],医疗科学[6],天文光谱数据分析[7-8]等许多领域。目前,离群挖掘方法主要包括:基于统计的方法(又称为基于模型的方法)[9],基于距离的方法[10],基于密度的方法[11],基于聚类的方法[12],基于网格单元的方法,基于角度的方法[13]等。基于网格单元的离群数据挖掘具有把以单个对象为单位的检测转换为以单元为单位的检测,能快速的修剪掉大部分非离群数据的特点,是一类典型的离群数据挖掘方法,具有重要的应用价值和应用前景。
基于网格单元的离群数据挖掘方法[14]大都是首先将数据集按属性维取值,均匀划分成网格单元;然后分析每个网格单元中所包含数据的分布,并修剪其正常数据的网格单元;对于含有正常和离群数据的网格单元,采用子网格单元划分、近似密度计算等方法,确定离群数据。典型研究工作主要有:Knorr等人首先提出了一种基于网格的离群数据挖掘方法,但该方法仅在小于4维数据下比较精确,并不适应于高维数据集。在文献[14]中,采用网格和密度结合的思想,提出了一种离群数据挖掘算法FOMAUC,有效提高了离群数据挖掘的效果和效率,但存在以下不足:
(1)在精选步骤2中,对各个数据对象的判别是独立的,未利用先前的判断信息,计算复杂性高,效率低;
(2)当维数较高时,稀疏网格单元的个数较多,造成精选过程时间复杂度高,因此不适用于高维数据。文献[15]为了解决文献[14]存在的计算复杂性高和效率低的问题,采用了微单元的概念。该算法通过增加微单元筛选过程,并采用改进的微单元树结构,避免对非空单元的操作和进行高效的邻居查找,但存在如下不足:
(1)采用微单元致使计算单元网格的密度次数增多,而且在高维空间中,微单元增加了时间开销;
(2)采用微单元,对于处理单元过程中保留的密集单元及密集微单元,直接认为是正常数据网格单元,直接删除;对于稀疏的微单元及其邻域微单元点数之和如果大于密度阈值,也判断为正常网格单元,这样容易遗漏离群数据。而且文献[15]只是在基于单元的基础上增加了微单元,在高维数据中,单元格密度较稀疏,造成几乎所有数据对象都为离群数据,因此该方法不适用于高维数据。张净等人提出了一种基于网格和密度的海量数据增量式离群点挖掘算法,该算法采用网格的七元组信息先对数据降维;然后利用增量更新减少内存需求,并过滤掉部分非离群数据;最后采用近似密度计算的方法减少计算量,从而确定出离群数据。 文献[16]给出一种基于P权值的离群数据挖掘算法,该算法首先采用三角不等式的剪枝技术修剪数据集,对剩余候选离群数据集用P权值的方法计算该数据对象与其k近邻的距离和,和越大,离群的可能性越大,但在距离和相等的情况下无法判断哪些数据对象更可能是离群数据。本论文的P权值方法是计算候选离群单元中数据对象与其k近邻的平均距离,由于候选离群单元中对象数不同,其邻域单元对象数也可能不同,因而每个对象的近邻数k可能也不同,因此求平均距离,平均距离越大,离群可能性越高。
综上所述,本文给出了一种基于网格单元和P权值的离群数据挖掘算法。该算法首先将数据集按维均匀划分为网格单元,并根据其包含的数据对象密度,筛选出非离群和离群网格单元;对于剩余网格单元,采用P权值的方法,来度量和确定离群数据。该方法有效地避免了离群数据遗漏和误检现象,进一步提高了挖掘精度。
1 单元网格、距离和离群数据
利用单元网格,可以快速识别离群数据和修剪正常数据,是一类典型的离群数据挖掘方法。参照文献[1,15,16],相关概念定义如下:
定义1 单元U.对于给定的m维数据集,将其构成m维空间S中的每一维均分,第i维被划分成Si段,那么,该空间就被划分为S1×S2×S3…×Sm个区域,这样的区域称为单元,记为U=(u1,u2,…um),1≤Ui≤Si.
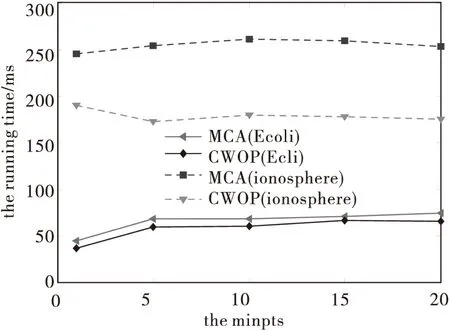
定义2 单元密度D.在m维空间S中有数据对象d=(d1,d2,…,dm),若点d属于单元U=(p1,p2,…,pm),当且仅当(pi-1)×L≤di 定义3 若一单元U中的密度D超过某一给定的阈值Minpts, 即D≥Minpts时, 则单元U称之为密集单元, 记为UD, 反之单元U称之为稀疏单元, 记为US. 定义4 邻居单元。若单元U1=(p11,p12,…,p1m)和U2=(p21,p22,…,p2m)满足下式: 其中i=1,2,…m,则称U1,U2互为邻居单元。 对于密集单元,若其邻居单元也都为密集单元,则将该单元中的点全部标记为正常数据,否则将其标记为候选离群单元。对于稀疏单元,若其邻居单元也都为稀疏单元,则将该单元中的数据对象标记为离群数据,否则将其标记为候选离群单元。 定义5 距离 令i=(xi1,xi2,...,xip)和j=(xj1,xj2,...,xjp)是两个p维数据对象。对象i和j之间的欧几里得距离定义为: 欧几里得距离有效地度量和刻画了两个数据对象之间的相似性,距离d(i,j)越大,二者越相异,越小越相似。 利用P权值可以有效地度量数据对象的稀疏程度,权值越大,对象p距离其邻域对象越远,也表明对象p的邻居对象越稀疏。 2.1 基本思想 在基于网格单元的离群数据检测方法中,对于候选离群单元中的数据,很难判别是否为离群数据,容易遗漏,而且在高维数据集中,网格单元密度较稀疏,无法有效地度量离群数据。P权值是一种度量数据对象稀疏程度的有效方法,采用P权值来度量候选离群单元中的数据对象,可以有效地区分和识别出每个数据对象的稀疏程度,从而有效地度量其网格单元中,所包含的离群数据。基本思想如下: (1)对于任意m维数据集DB,根据定义1,将其构成m维空间数据S中的每一维均分,即将m维数据空间划分为多个网格单元U.(2)根据定义2,统计每个单元的密度D.(3)根据定义3,4划分密集单元和稀疏单元,若该单元为密集单元,且其邻居单元也都为密集单元时,可以确定该单元中所有的数据都为正常数据,否则将其标记为候选离群单元。若该单元为稀疏单元,若其周围邻居单元都为稀疏单元,则可判定该单元所有数据都为离群数据,否则将其标记为候选离群单元。(4)对标记为候选离群单元中的数据对象,根据定义5,6计算其P权值,确定前TOP-N个P权值最大的数据对象即为最需要的离群数据。(5)综上,标记为离群数据单元的对象和前TOP-N个P权值最大的数据对象即为最终查找的离群数据。 2.2 算法描述 算法:CWOP(Cell-basedandPweightoutlierdetection) 输入:数据集GDB,密度阈值Minpts,近邻数k 输出:离群数据集合O 1.double[][]data=GDB; 2.doublelen; 2.createNetGrid(double[][]data,doublelen);//根据数据集和单元格边长创建网格 3.showPointsSum(ArrayListresult,Stringname);//统计每个单元格的对象数 4.statisticNeighourCellUnit(ArrayListresult);//统计邻域单元的对象数 5.foreachnon-emptyCkinD//对于每个非空单元 6.ifCountk>MinptsandCountk邻域>Minpts 7.Ckisnormaldata,skiptoanotherCk.//标记此Ck为正常单元,跳转到下一个单元 8.elseifCountk 9.Ckisoutlierdata,addCktooutlierCell,skiptoanotherCk. 10.endif 11.foreachnon-emptyCkinG//对于剩余网格单元 ,计算每个对象的P权值 12.foreachOiinCk 14.fori=1tom 15.ArrayListgetAllOutPoints(ArrayListcolorcells,ArrayListobletepoints,intm),addtooutlierCell. 16.returnoutlierCell.//输出离群数据集合中的点 2.3 单元格边长L的确定 单元格边长对离群数据的判定有一定的影响,而一个特定的网格单元边长L无法适合于所有数据集D.单元格边长越小,网格单元的数目越多,统计单元格内的对象数执行时间就越长;单元格边长越大,虽然统计单元格内对象数时间缩短,但也降低了修剪概率。因此需要多次试验找出一个合适的单元格边长。 在上述CWOP算法中,首先使用基于网格的方法将数据划分网格单元,再利用网格的密度特征,有效地确定数据集中一部分非离群单元和离群单元。对于候选单元中的点用P权值的方法可以确定对象分布的稀疏程度,权值越大,该对象周围越稀疏,说明该对象距离其邻域对象越远,即越可能是离群数据,从而检测出这些网格单元中的离群数据。对于检测高维数据中稀疏网格单元,确定前n个权值最大的数据为离群数据,也不会造成所有数据都检测为离群数据这一现象。假设已统计好数据集中数据量为N,稀疏单元的个数为s,稀疏单元邻居个数为k,密集单元内数据对象的个数为c,扫描剩余候选集,判断该数据对象是否为离群数据,需要调用m次,因此算法总的时间复杂度为T=O(N+2*s*k+(N-c)*m). 通过实验对本文CWOP算法和改进的微单元(MCA)算法[15]的检测精度、执行效率和冗余度进行对比。 精确度=(挖掘出的离群个数/实际离群个数)*100% 冗余度=(已挖掘的离群点数-正确挖掘的离群点数)/已挖掘的离群点数 实验环境:Intel(R)Core(TM)i5-4570,3.20GHzCPU,2GB内存,操作系统为Windows7,用junoeclipse作为开发平台,并用java语言实现了MCA算法[15]和本文CWOP算法。 测试数据集如下: 表1 试验测试数据集 对于低维数据,图1表明算法的精度随着L的增大呈现先降低后升高的状态,在边长为0.3至0.5和1.3时达到最佳为77.8%,随着边长L的增大,划分的单元格数量减少,每个单元格内的对象数增多,选定合适的密度阈值,删除的非离群点数增多,因此精度提高。说明单元格边长对该算法挖掘精度影响很大。特殊情况,当边长L=1时,所有对象都在一个单元格内,此时CWOP算法判定所有对象为候选离群点,以做进一步判断,而MCA算法判定该单元为密集单元,这样造成所有对象都为非离群数据的极端情况,相当于没有检测到离群数据对象,即造成离群数据判断不精确。 对于高维数据,从图1直观来看,二者的挖掘精度都达到100%,但二者的冗余度却不同,具体看下面的实验对比。 图1 挖掘精度比较(Minpts=15) 图2 挖掘精度比较(L= 0.5) 图2为在L固定的时候,改变密度阈值来比较两个算法的挖掘精度,随着密度阈值的增加,MCA算法和CWOP算法精度都呈现升高的趋势。在Minpts=5和25的时候达到最高峰。在找到合适的边长之后,调整Minpts的大小,在Minpts=1至5时,CWOP算法挖掘精度稍高于MCA算法,在Minpts=10至25时,二者都达到最高精度77.8%.总体来说,在数据集维数比较低时,CWOP算法挖掘精度比MCA算法略高。 对于高维数据,从图1和图2可以看出两种算法的精度都达到100%,但是从图3可以看出CWOP算法的冗余度为0,而MCA算法的冗余度为97%.MCA算法在检测过程中虽然删除了一部分非离群点,但是仍旧把很大一部分当成离群点,而真正的离群点数是少数的,这就造成离群点检测的冗余度较高,这是离群点的误检,说明MCA算法不适合检测高维数据。而CWOP算法采用P权值有效地度量数据对象的稀疏程度,可以正确的检测出离群点并且冗余度为0. 图4和图5表明随着L的增大或Minpts的增大,删除的非离群点数越来越多,主要原因是,随着单元格边长的增大,划分单元格的数目减少,在Minpts固定时,边长大的单元格中对象数较多,删除的非离群点数较多,因此执行时间减少,效率提高。在L固定时,随着Minpts的增大,单元格中大于Minpts的单元数减少,删除的单元格数减少,因此执行时间减少,效率提高。从图4和图5可以看出,在低维情况下,CWOP算法的效率略高于MCA算法,而在高维情况下,CWOP算法的效率明显高于MCA算法。而且在高维和海量数据情况下,MCA算法的冗余度达到100%,说明MCA算法不适合检测高维数据。 图3 冗余度比较 图5 效率比较(L=0.5) 图6 不同数据集大小下用的时间比较 图6为在选定合适的Minpts和边长的情况下,在不同数据集大小下所用时间的比较,CWOP算法由于数据量的增加,计算每个对象的P 权值所用时间增加,因此效率降低。而MCA算法随着数据量的增加,划分微单元并统计微单元内的对象数增加了计算量,效率也随之降低。可以看出CWOP算法和MCA算法都随着数据集数目的增多所用时间增大,而且都成指数增长,而CWOP算法所用时间略低于MCA算法,说明CWOP算法的效率略高。将该算法与OMAW算法[17]进行比较,该算法在数据集达到3 000时明显优于OMAW 算法,说明数据量增大时,本文算法的效率相对较高。 采用基于网格单元的离群数据挖掘方法修剪网格单元,对剩余的网格单元用P权值的方法确定离群数据,即计算候选点O的k近邻的平均距离,并按P权值大小排序,确定前TOP-N个P权值最大的点即为离群点,具有既可以检测出既有正常数据又有离群数据网格单元中的离群数据的优点,也可以避免在高维数据中把所有稀疏单元都检测为离群数据这一极端现象。利用UCI数据集,实验验证了该算法的可行性和有效性。 [1] JIAWEI H,MICHELINE K. FAN M. Data mining concepts and techniques[M].Beijing:China Machine Press,2012.7 [2] KNORR E M, Ng R T. Algorithms for Mining Distance-Based Outliers in Large Datasets[C]// Proceedings of the 24rd International Conference on Very Large Data BasesMorgan Kaufmann Publishers Inc., 1998:392-403. [3] SEQUEIRA K, ZAKI M. ADMIT: anomaly-based data mining for intrusions[C]//Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2002: 386-395. [4] LAZAREVIC A, ERTOZ L, KUMAR V, et al. A Comparative Study Of Anomaly Detection Schemes In Network Intrusion Detection[C]// In Proceedings of the Third SIAM International Conference on Data Mining2003. [5] LIU H, SHAH S, JIANG W. On-line outlier detection and data cleaning[J]. Computers & Chemical Engineering, 2004, 28(9):1635-1647. [6] KNORR E M, NG R T, TUCAKOV V. Distance-based outliers: algorithms and applications[J]. The VLDB Journal—The International Journal on Very Large Data Bases, 2000, 8(3-4): 237-253. [7] 张继福, 蒋义勇, 胡立华,等. 基于概念格的天体光谱离群数据识别方法[J]. 自动化学报, 2008(9):1060-1066. [8] 张继福, 李永红, 秦啸,等. 基于MapReduce与相关子空间的局部离群数据挖掘算法[J]. 软件学报, 2015 (5):131-135. [9] FREEMAN J. Outliers in Statistical Data (3rd edition)[J]. Journal of the Operational Research Society, 1995, 46(8):68-71. [10] 石岩,刘爱琴,张继福.一种基于基尼指标的高维数据离群挖掘算法[J].太原科技大学学报, 2013, 34(3):161-165. [11] BREUNIG M M, KRIEGEL H P, Ng R T, et al. LOF: Identifying Density-Based Local Outliers.[J]. Acm Sigmod Record, 2000,29(2):93-104. [12] LIANG B M. A Hierarchical Clustering Based Global Outlier Detection Method[C]// Bio-Inspired Computing: Theories and Applications (BIC-TA), 2010 IEEE Fifth International Conference2010:1213 - 1215. [13] KRIEGEL H P, S HUBERT M, ZIMEK A. Angle-Based Outlier Detection in High-dimensional Data[J]. Dbs.ifi.lmu.de, 2008(6):444-452. [14] 崔贯勋,李梁,王勇,等. 快速的基于单元格的离群数据挖掘算法[J]. 计算机应用, 2009, 29(12): 3300-3302. [15] 唐成龙, 邢长征. 基于数据分区和网格的离群点挖掘算法[J]. 计算机应用, 2012, 32(8): 2193-2197. [16] 张净, 孙志挥, 杨明, 等. 基于网格和密度的海量数据增量式离群点挖掘算法[J]. 计算机研究与发展, 2011, 48(5): 823-830. [17] LOU S J, ZHANG J F, LIU A Q. A Outlier Mining Algorithm Based on P Weights[J]. Journal of Chinese Computer Systems, 2014,12(6):63-68. AnOutlier Data Mining Method of Grid Cell-Based and P weights FENG Ting-ting,ZHANG Ji-fu (School of Computer Science and Technology, Taiyuan University of Science and Technology, Taiyuan 030024, China) Cell-based outlier data mining is a kind of typical outlier data mining method, although it has the advantage of quick identification of outlier data and trimming the data from the group, only from the unit part perspective of pruning the non-outlier data is likely to make some cells not be determined accurately. This paper presents a cell-based and P weight of outlier data mining algorithm. The algorithm firstly divides each dimension of the data set and divides the grid cell, then in the grid cell, screens out the outlier data and the normal data grid cell; both contain outlier and the normal data of grid cell by using the method of p weights to measure and determine the outlier data from the group, so as to further improve the accuracy of outlier data mining; finally, the experiment proves the algorithm of the feasibility and effectiveness by using the UCI data sets. data mining, outlier data, grid cell, P weight, distance 2015-11-05 冯婷婷(1988-)女,硕士研究生,研究方向为数据挖掘。 1673-2057(2016)05-0359-06 TP39 A 10.3969/j.issn.1673-2057.2016.04.005
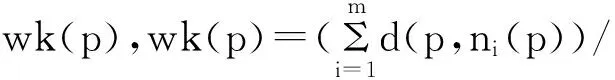
2 基于单元和P权值的离群数据挖掘算法

3 算法分析
4 实验结果与分析





5 结 论
