轧辊随机磨损模型及其最优更换策略研究
2016-11-14张晓红曾建潮
张 炯,张晓红,曾建潮,赵 静
(太原科技大学工业与系统工程研究所,太原 030024)
轧辊随机磨损模型及其最优更换策略研究
张 炯,张晓红,曾建潮,赵 静
(太原科技大学工业与系统工程研究所,太原 030024)
轧辊是轧机上使得轧件产生塑性变形的主要功能部件以及轧制过程中的主要消耗零部件,其磨损程度直接影响着轧制产品的产量与合格率。由于现有轧辊的定期更换周期来源于轧辊厂商的实验或轧钢厂的长期运行经验,容易导致轧辊的过早或过晚维修。针对这一问题,以某厂1780 mm热连轧轧辊为对象,从概率论和可靠性理论的角度出发,利用轧辊每次更换和检测所得的大量修磨数据,研究并建立轧辊磨损的随机可靠度模型,并在此基础上建立以平均最小更换成本为目标的最优更换模型。通过实例计算得到了符合实际生产状况的轧辊最优更换周期,检验了所建模型的可行性和有效性。
轧辊表面磨损;随机磨损建模;可靠度;更换策略优化
轧辊是轧机上使轧件发生塑性变形的重要部件以及轧制过程中主要的耗材。轧辊的表面磨损和失效是影响轧材产量和合格率的主要因素[1-2]。因此,深入探究轧辊的磨损机制及其磨损计算模型,进而制定轧辊的合理更换与修磨策略,对确保轧制设备持续、有效运作和提高轧材的产量与合格率有着及其重要的意义。
由于轧辊的生产成本和购买价格很高,因此轧钢厂通常对轧辊进行周期性地更换与修磨之后再次使用。目前,轧钢厂多数采用轧辊厂商提供的实验更换周期或企业长期运行的经验更换周期对其进行更换与修磨。依此而制定的轧辊更换策略并没有考虑轧辊的实际运行状况,可能会导致轧辊的过早或者过晚维修问题。轧辊的表面磨损受到轧制循环应力、轧制材料、轧制环境(如温度、湿度)等各种随机生产因素的影响,其实际磨损是一个动态随机过程。从轧辊磨损的随机性出发,研究轧辊的更换与修磨周期才具有科学性和实际指导意义。
前期国内外关于轧辊的研究鲜有涉及轧辊更换周期方面,大多数都侧重于轧辊磨损原因及其修复技术、磨损机理特性和磨损预测模型等方面。陈兵等[3]针对酸轧机组工作辊磨损快、有效轧制寿命短的问题,借助大批轧辊磨损实验数据分析其磨损机理,进而建立轧辊的磨损量计算模型,最后采用遗传算法对相关的参数进行优化。滕洪宝[4]研究并建立了带钢热连轧轧辊磨损量计算模型,进而开发出在visual studio2008环境下的仿真软件对现场轧辊磨损进行监控。大多数研究给出了轧辊磨损的预测模型,但此类模型并不能反映不同运行条件下轧辊的随机磨损特性。由于轧辊实际磨损过程与裂纹随机扩展过程有很强的相似性和可借鉴性,因而可以参考裂纹扩展的随机模型研究方法来建立轧辊的随机磨损模型,进而在此基础上研究轧辊的最优更换策略。
本文参考裂纹随机扩展模型的建模过程,并从概率论和可靠性理论的角度出发,以轧辊磨损机理和可获得的轧辊修磨数据为基础,首先研究并建立了轧辊磨损的随机可靠度模型,在此基础上建立以平均更换成本最小为目标的最优更换模型,最终通过实例验证了本文提出的轧辊最优更换策略研究方法的可行性。
1 轧辊磨损研究
1.1 轧辊磨损特性及机理
轧辊磨损和普通的金属磨损在形成机制上是大体一致的,从摩擦学理论分析,其磨损表现为轧辊直径不断地磨损变小。在几何特性和物理条件上又与普通的金属磨损有着很大的区别,如在轧制过程中轧辊受到周期性负荷的作用和环境温度的变化,同时和环境中的各种介质互相影响,置于氧化环境之中;轧辊辊面与轧件因周期性的接触而产生的复杂的滑动摩擦、滚动摩擦等。轧辊磨损机理极其复杂,形式多样,其中疲劳磨损是轧辊磨损主要的表现方式。轧辊疲劳磨损的影响因素众多,其中关键的因素为轧制力、轧制里程(长度)、带钢宽度厚度规格、轧件材质、轧辊材质和润滑状况等。在轧制过程中,各种因素共同作用、彼此影响,加之这些因素多呈现时变性的特点,从而加剧了轧辊磨损现象的复杂性。
1.2 轧辊磨损模型
从轧辊磨损机理出发,研究轧辊磨损量预测模型的工作极其困难,当前国内外学者对轧辊磨损数学模型的研究大多数是从考虑轧辊磨损过程中的主要影响因素,现场搜集数据,采取回归解析的方法,得到经验与理论相结合的确定性模型。目前极具代表性的轧辊磨损计算模型便属于这种回归模型[5],文献[5]中轧辊磨损模型具体形式如下:
(1)
其中:△w为磨损增量;a为磨损换算待定系数;b为磨损换算系数常数部分;Dw为轧辊直径;f为前滑值;Hin为轧件入口厚度;Hout为轧件出口厚度;ld为接触弧长;α为轧制力影响指数;β为磨损距离影响指数;Bw为轧件宽度;HR为工作辊硬度;π为圆周率;△l为带钢轧制长度;i为辊身计算位置标记。
在实际的轧制过程中,轧制力沿轧件横向的分布是变化的,由此导致轧辊表面磨损沿轧辊横向的分布也是不均匀的,因而引入轧制力P′的修正参数,其算法如下:
(2)
其中:dw为边部负载宽度;kw为边部负载倍率;△X为计算分割宽度。
由于轧辊材料微观构造的不匀称性、构成物质的不匀称性、缺陷分布的不匀称性,轧辊磨损沿其横向的分布不均匀,为保证轧制过程中轧辊的平衡性和轧材质量,轧件通常被置于轧辊中部轧制,因而轧辊通常中部磨损迅速和磨损程度大,边部磨损缓慢和磨损程度轻。因此研究轧辊中部磨损规律对轧辊的更换具有更切实际的指导意义。由式(1)得到轧辊中部磨损计算形式:
(3)
其中:△w为轧辊中部磨损增量。
为方便计算,式(3)可以简化为成下形式:
△w=(aDw+b)AαBβC
(4)
其中:A为轧制负荷影响项;B为变形区几何形状影响项;C是轧辊转动的圈数。
A、B、C具体表达形式如下:
(5)
分析模型中A、B、C的取值,可知其取值与轧辊直径Dw、轧件宽度Bw、轧件入口厚度Hin、轧件出口厚度Hout有关,在轧制条件确定的情况下,这些量通常是可确定的,A、B、C的取值也就确定了,进而式(1)、(3)、(4)所表示的轧辊磨损增量便确定了。由于在轧制生产过程中,这些因素协同作用、相互影响,而且多呈现随机特性,实际的轧辊疲劳磨损增长具有随机特性,即轧辊疲劳磨损增长并不是确定性过程,而是与轧制累积长度相关的随机过程。由此,本文以上述参考模型为基础,通过引入随机项来刻画轧辊磨损过程的动态、随机特性,即将确定性的轧辊疲劳磨损增长模型随机化。
2 轧辊疲劳磨损增长随机模型
轧辊疲劳磨损随机模型的建立以式(3)为基础,对模型中的关键参数——磨损量影响系数b和轧制力影响指数α作这样的处理[6]:将b和α都当作随机变量,非关键参数α和β作常数处理。对于参数α和β,以1 780 mm热连轧轧机轧辊[5]为例,取a=0,β=1并带入式(3),求得轧辊疲劳磨损率计算公式:
(6)
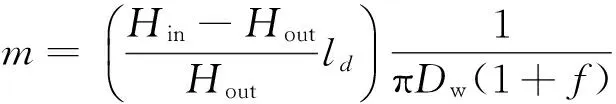
(7)
轧辊疲劳磨损增长与疲劳裂纹扩展在很多方面具有相似之处,如都承受变化的循环载荷的作用,二者的机理模型在形式、原理上具有相似性和可借鉴性,在本质上都是确定性数学模型,但实际的增长过程都具有动随机特性。目前最容易被接受、且具有简单表达形式的疲劳裂纹扩展模型[6-9]为:
da/dN=D△km
(8)
其中:D、m为材料参数;△k为应力强度因子幅度。
有关疲劳裂纹增长的文献大多采用概率理论的方法来研究其扩展原理,建立疲劳裂纹增长率的概率解析模型[6-11]。文献[6-7]中指出裂纹扩展速率da/dN=D△km的参数D和m是随机变量。对D和m的随机特性已有很多研究,文献[11]指出D和m分别服从对数正态分布和正态分布。
裂纹扩展率模型da/dN=D△km中的参数D和m与轧辊单位轧制磨损增量模型△w/△l=GAα中的参数G和α具有很强的相似性和借鉴性。与裂纹随机扩展模型相对应,将轧辊磨损率模型△w/△l=GAα中的参数G和α随机化处理,假设G和α相互独立且分别服从对数正态分布和正态分布,进而由G和α推导轧辊疲劳磨损率的随机分布情况。
式(7)两边取对数得:
In(△w/△l)=InG+αInA
(9)
由概率论[12]的知识可知:
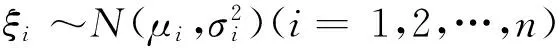
(2)若随机变量ξ~N(μ,σ2),则有exp(ξ)~InN(μ,σ2);
(3)若随机变量ξ~InN(μ,σ2),则有In(ξ)~N(μ,σ2).
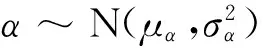
μσInA=μγ+μαInA
(10)
式(9)两边取方差:
D{In(△w/△l)}=D{InG+αInA}=D{InG}+
(11)
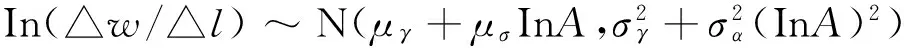
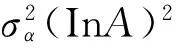

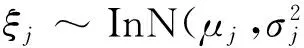
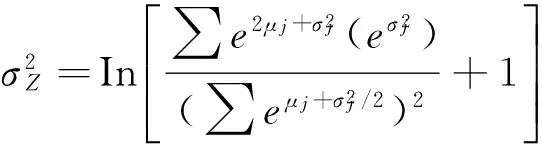
(12)
当所有的ξj具有相同的标准差,即σj=σ时,上式可以简化为:
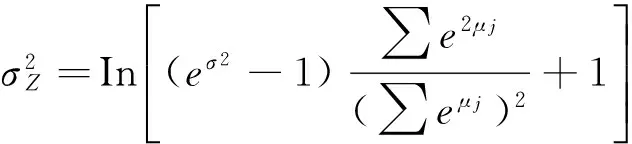
(13)
关于机械设备磨损的可靠性,工程上普遍采取的故障判别标准[16]为实际磨损程度超过极限磨损阈值,即当实际磨损程度不大于极限磨损阈值时运行正常,当实际磨损程度大于极限磨损阈值时失效。由此可得,当假设新轧辊或者修磨如新的轧辊在轧制n个单位长度轧件后的累积磨损量和轧辊容许的极限磨损量分别为w(n)、df时,计算轧辊磨损可靠度的极限状态方程为:
M=M(Df,w(n))=Df-w(n)=0
(14)
由概率论的知识[12]可知,若Y=In(X)服从正态分布,则有:
P(Y≤y)=P(eY≤ey)=P(X≤x)
(15)
由此可得,轧辊轧制n个单位长度轧件后对应的磨损失效概率pf(n)的表达式为:
pf(n)=P(Df-w(n)≤0)=1-P(w(n)<
Df)=1-P(Inw(n) (16) R(n)=1-Pf(n)= (17) 轧辊对应的磨损失效概率为: (18) 目前,在机械设备维修工作中主要采用故障后维修和预防性维修两种策略,预防性维修包括定期性维修与视情维修两种方式,其中,定期维修[17-18]为降低设备故障的发生几率与性能的退化,通常依据事先确定的维修周期或者指标来实施维修计划。由于轧辊磨损状态的在线监测难以实现,因此,在轧材实际生产过程中通常对轧辊采用定期维修策略。定期维修间隔期的长短直接关系到定期维修工作是否经济、有效,而基于可靠性理论的维修决策的主要研究工作就是优化定期维修策略的维修周期。 设轧辊的定期更换周期为n个单位轧制长度,对轧辊进行更换与修磨,更换的时间忽略不计,轧辊正常更换的成本为CP(包括人工费和轧辊修磨费用),轧辊故障后的平均更换费用为CU(包括人工费、轧辊成本、设备损失成本、轧材损失成本等),则轧辊在轧制n个单位长度轧件时的平均维修费用Cr(n)计算式为: (19) 其中:R(n)为轧辊累积轧制n个单位轧制长度轧件时的可靠度,Pf(n)为轧辊累积轧制n个单位轧制长度轧件时的失效概率。 针对某厂1 780 mm热连轧带钢生产,对优化问题(19)进行求解,研究其粗轧R1四辊轧机工作辊的随机磨损特性,确定其更换周期。该轧钢厂提供的有关其粗轧R1四辊轧机工作辊中部磨损量与对应的轧制带钢长度数据如表1所示: 表1 轧辊部分修磨数据表 表2 模型参数表 求解可得轧辊平均维修成本随轧制单位的变化如图1所示。 分析图1中的成本曲线可知:当n小于80,即轧制带钢卷数小于80卷时,因为轧辊的磨损失效率低,对轧辊进行更换会出现维修过度的现象,从而导致了轧辊的平均维修成本过高;当n大于80时,因轧辊出现磨损失效的概率过大,对轧辊进行更换会出现维修不足的现象,从而轧辊的平均维修成本高;当n等于80时,即每轧制80卷带钢换辊一次,此时轧辊的磨损失效概率适中,平均维修成本低。 图1 轧辊平均维修成本 (1)建立了轧辊磨损的随机可靠度模型,能够较合理的反应在实际轧制条件下轧辊磨损过程的动态性和随机性。 (2)算例验证了轧辊随机磨损建模和在此基上建立的轧辊最优更换策略的可行性。 (3)该钢厂生产部门的实际更换策略是当轧制带钢卷数处于(85,90)之间进行更换,而模型计算所得的轧辊更换周期小于此经验周期;以模型计算所得的更换周期对轧辊进行更换操作时,轧辊的磨损程度接近其磨损极限,更换成本低,能确保轧辊低故障停机概率的前提下,尽可能地提高轧辊的使用率,从而提高轧钢厂的经济效应。 (4)鉴于轧辊磨损机理与磨损过程的复杂性,文中只探究了影响轧辊磨损的关键因素的随机特性,而忽略了轧制速度、轧辊硬度等轧制工艺在一定范围内的随机波动,这方面有待进一步的深入研究。 [1]孟丽军,胡玲,董有宝,等.热轧轧辊失效分析及预防措施研究[J].科技与企业,2015(9):240. [2]PALIT P,JUGADE H R,JHA A K,et al.Failure analysis of work rolls of a thin hot strip mill[J].Case Studies in Engineering Failure Analysis,2015(3):39-45. [3]陈兵,林海海,吴迪平.酸轧机组拉矫机工作辊磨损预测模型研究[J].轧钢,2014(3):1-4. [4]滕洪宝.带钢热连轧轧辊磨损的研究[D].沈阳:东北大学,2012. [5]曹燕,钱春风,刘相华,等.1780mm热轧机组轧辊磨损模型参数的优化[J].轧钢,2010,27(2):24-27. [6]白鑫,谢里阳.平稳随机载荷历程下的疲劳裂纹扩展规律预测[J].航空学报,2014(9):2500-2505. [7]曹世豪.钢轨表面疲劳裂纹的扩展与预防研究[D].成都:西南交通大学,2014. [8]石凯凯,蔡力勋,包陈.预测疲劳裂纹扩展的多种理论模型研究[J].机械工程学报,2014,18:50-58. [9]于锋礼.飞机声疲劳裂纹扩展的分析方法研究[J].科学技术与工程,2014,12:146-149. [10]刘益华,王奇志,李丽远,等.基于损伤力学的疲劳裂纹扩展分析[C]∥中国航空学会第6届中国航空学会青年科技论坛文集,北京:航空工业出版社,2014:5. [11]张啸尘,谢里阳.概率疲劳裂纹扩展速率统计分析方法研究[C]∥中国机械工程学会可靠性工程分会、浙江理工大学机械与自动控制学院,2013年全国机械行业可靠性技术学术流会,北京:机械工业出版社,2013:5. [12]茆诗松,贺思辉.概率论与统计学[M].武汉:武汉大学出版社,2010. [13]SUNKLODAS J K.L 1 bounds for asymptotic normality of random sums of independent random variables[J].Lithuanian Mathematical Journal,2013,53(4):438-447. [14]LIFSHITS M A.Cyclic behavior of the maximum of sums of independent random variables[J].MAI,2013,412:207-214. [15]GAO,X.,H.XU,D.YE.Asymptotic Behavior of Tail Density for Sum of Correlated Lognormal Variables[J].International Journal of Mathematics and Mathematical Sciences,2013:211-229. [16]孙永全,刘剑,任和,等.基于累积磨损量分布的飞机刹车片可靠性分析[J].航空维修与工程,2015(1):85-88. [17]FOULADGAR,M.M.,A.YAZDANI-CHAMZINI,A.Lashgari et al.Maintenance strategy selection using AHP and COPRAS under fuzzy environment[J].International journal of strategic property management,2012,16(1):85-104. [18]SHAFIEE,S.DUFFUAA.Maintenance strategy selection problem:an MCDM overview[J].Journal of Quality in MaintenanceEngineering,2015,21(4):378-402. Research on Stochastic Wear Model of Roller and Its Optimal Replacement Policy ZHANG Jiong,ZHANG Xiao-hong,ZENG Jian-chao,ZHAO Jing (Division of Industrial and System Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China) Roller is an important tool for rolling plastic deformation and is the mill's main consumption part,its wear degree directly influences the production and the qualified rate of rolled products.The existing regular replacement cycle of roller that easily leads to maintenance too early or too late is got from roll manufacturers′ experiments or rolling mill′s long-term running experiences.The optimal replacement model of the minimum average replacement cost is established based on the random reliability model of roll wear which takes the factory 1780mm hot strip rolling roll as an object and uses the roller grinding data from each replacement and test data of roll grinding from the perspective of probability theory and reliability theory.The feasibility and effectiveness of the model are verified by an example to calculate the optimal replacement cycle of roll that conforms to actual production situation. roll surface wear,stochastic wear modeling,reliability,replacement strategy optimization 2015-11-24 国家自然科学基金(61573250);山西省自然科学基金资助项目(2014011019-2) 张炯(1989-),男,硕士研究生,主要研究方向为系统的故障预测与健康管理。 1673-2057(2016)05-0379-06 TG331 A 10.3969/j.issn.1673-2057.2016.04.009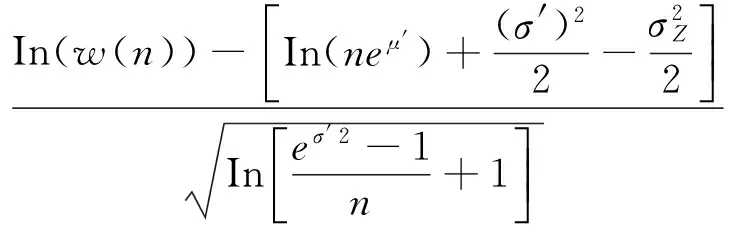
3 轧辊更换策略的确定与优化
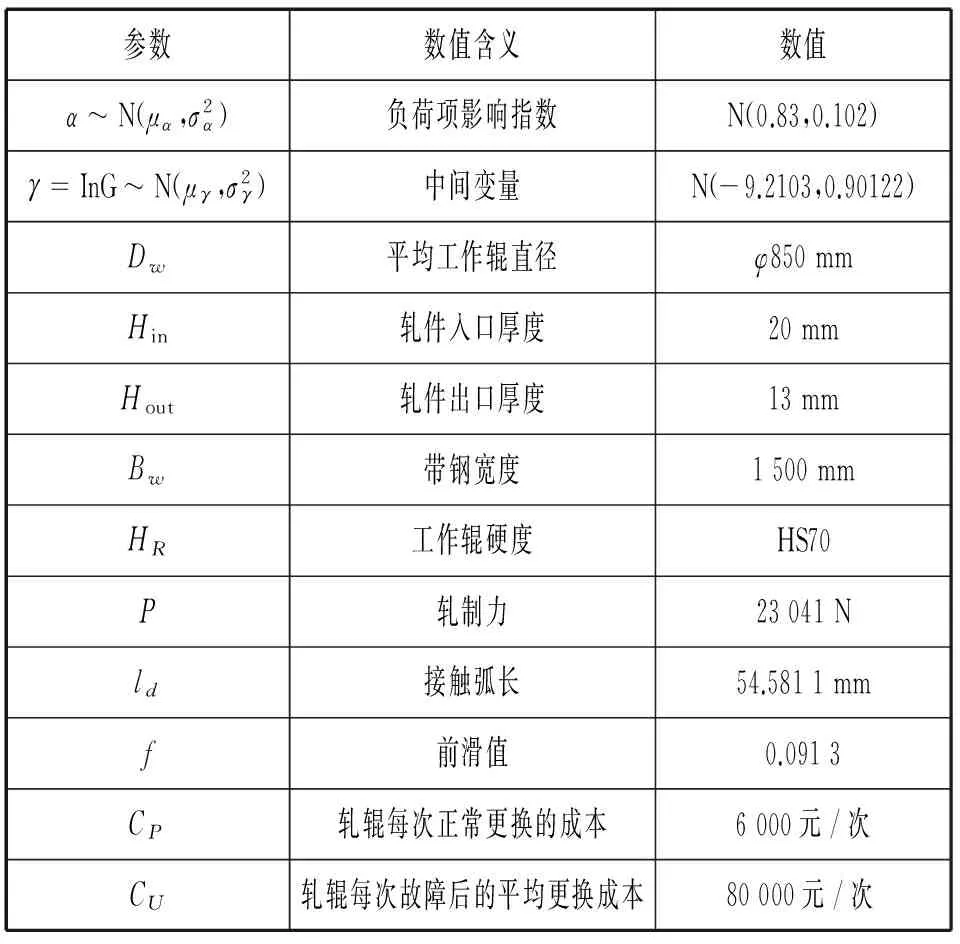
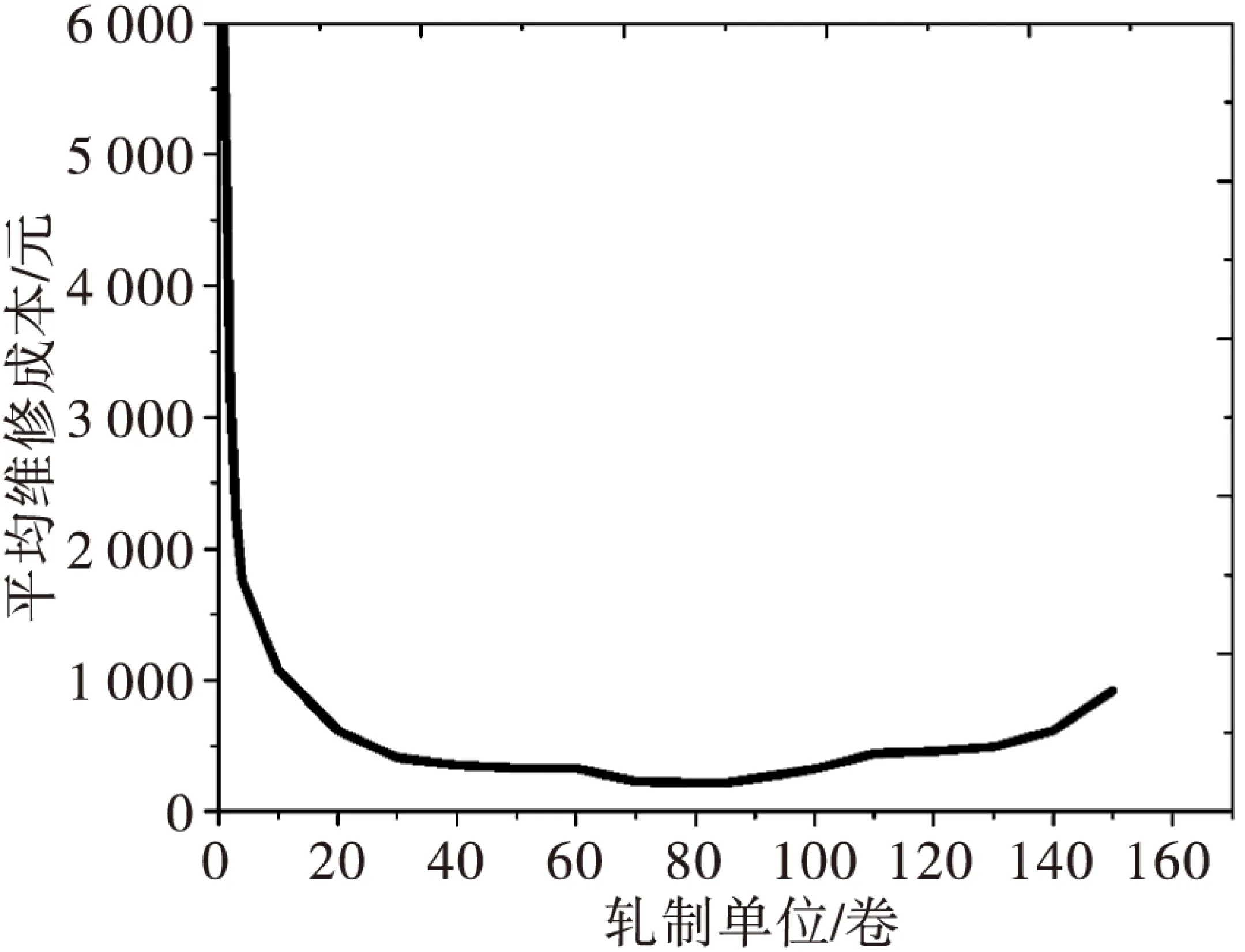
4 实例研究

5 结论
