动导数数值预测中的相关问题
2016-11-14袁先旭陈琦谢昱飞陈坚强
袁先旭, 陈琦, 谢昱飞, 陈坚强
中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
动导数数值预测中的相关问题
袁先旭, 陈琦, 谢昱飞*, 陈坚强
中国空气动力研究与发展中心 计算空气动力研究所, 绵阳621000
动导数是飞行器动态稳定性分析、弹道设计和控制系统设计的重要参数,其预测方法主要有工程近似方法、数值模拟和风洞试验。基于动导数、交叉导数的概念,介绍了强迫振荡法、自由振荡法等预测动导数的数值模拟方法,重点就超声速、高超声速动导数数值预测中存在的问题开展讨论,包括时间步长、子迭代步数的选取;振荡频率对辨识结果的影响;强迫振荡法和自由振荡法辨识动导数可能存在差异的原因分析;交叉导数和交叉耦合导数的辨识问题以及飞行器构型对动导数预测的影响等。并结合算例进行了具体分析,在总结现有研究经验的同时,针对当前研究中存在的困惑和难题,提出了相应的改进建议。
动导数; 交叉导数; 强迫振荡; 自由振荡; 振荡频率
动导数是飞行器控制系统设计中的重要参数之一,对飞行器的动态稳定性和飞行品质有重要影响。随着现代先进飞行器对机动性和敏捷性的要求越来越高,特别是大迎角机动飞行时,传统上视为小量而被忽略的交叉导数和交叉耦合导数也逐渐引起人们的重视。总体来看,随着飞行器机动性能的提升,动导数的重要性也日益凸显。
在20世纪90年代以前,动导数的预测方法主要是经验和半经验方法,典型的有修正牛顿理论、内伏牛顿流理论、牛顿-玻尔兹曼理论以及修正激波-膨胀波理论等[1]。90年代之后,随着计算流体力学(CFD)技术和计算机硬件水平的迅速发展,数值求解Euler/Navier-Stokes方程获取动导数的方法迅速普及。通过数值模拟强迫振荡过程或自由振荡过程获取动导数的方法,国内外都开展了广泛的研究工作,国外如Weinacht[2]和Qin等[3];国内如刘伟[4-6],袁先旭[7-9]等较早开展了动导数的数值模拟预测研究工作。
2010年左右,采用数值模拟方法预测动导数的文献在国内开始大量涌现,研究外形也不再是单一的钝头体,开始向各种复杂外形发展,研究内容也不断丰富,促进了数值预测动导数方法的发展。但时至今日,动导数数值预测中仍然存在很多困难和疑问,需要深入开展相关的研究工作。本文以讨论的形式,在总结现有工作的同时,对当前数值预测动导数中存在的问题进行剖析。期望通过对存在问题的讨论和研究,达到共同促进数值预测动导数技术发展的目的。
1 动导数概念
动导数的概念来自工程设计,长期以来,对动导数的确切含义仍存在不同看法和争议,导致在非定常气动力建模方面也不尽一致。
一般认为,最早的数学模型由Bryan和Williams[10]首先提出,Bryan将气动力、力矩视为扰动速度、控制角度和其速率的瞬时值的函数,以俯仰为例,即
(1)
式中:Cm为俯仰力矩系数;α和β分别为迎角和侧滑角;p、q和r分别为偏航、俯仰和滚转角速度。Tobak和Schiff[11]采用指示函数作为气动力的泛函,建立了非线性指示泛函理论。仍以俯仰为例,其非定常动态俯仰力矩的依赖关系为一微分-积分系统:
Cm(t)=Cm(t0)+
(2)
式中:L和V∞分别为参考长度和来流速度;Cm α和Cm q分别为俯仰力矩系数对迎角和俯仰角速度的导数;ξ∈[t0,t]。虽然式(2)在数学上是完备的,但非线性指示函数的确定非常困难,不可能直接求解这一微分-积分系统,必须对其进行简化处理。
Etkin和Reid[12]认为,非定常气动力、力矩是状态变量的泛函。在任何给定的时刻决定气动力的流场实际上不仅取决于瞬时的姿态,严格来说还和它的整个过去的历史有关,这个泛函关系式为
L(t)=L(α(τ))∞≤τ≤t
(3)
任玉新和刘秋生[13]利用Tobak和Schiff的非线性指示函数的方法,发展了改进的Etkin模型,在基准状态参数中包含了时间变量,扩展了动导数的应用范围。
这里根据Etkin模型,给出动导数的概念。对式(3),当α(τ)可在t附近展开为收敛的泰勒级数时,有
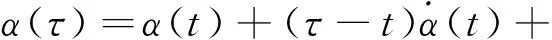
(4)


(5)
(6)
据此,以俯仰运动为例,可给出动态俯仰力矩系数的表达式:
(7)
取α0为平衡迎角,θ为俯仰角,定义为θ=α-α0。将式(7)在平衡迎角α0处进行泰勒展开,可得到
(8)

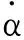
2 动导数数值预测方法
数值预测动导数,目前常用的方法主要有强迫振荡法和自由振荡法两种。以俯仰方向为例,强迫振荡法一般是给定一个如下形式的简谐振荡:
α=α1+θ=α1+αmsin(2πft)
(9)
式中:α1为振荡起始迎角;αm为振荡幅值;f为振荡频率。通过数值求解飞行器作强迫俯仰振荡的时间历程,即可给出动态俯仰力矩系数Cm的时间历程曲线和Cm-α迟滞圈。根据动态气动力模型式(8),略去二阶项和高阶项,对上述迟滞圈在一个周期内进行积分,即可辨识得到迎角α1处的动导数,即
(10)
式中:Cm0为起始迎角处的俯仰力矩系数;T为振荡周期。自由振荡法则是放开飞行器的转动自由度,飞行器在自身气动力矩的作用下自由振荡。仍以俯仰为例,单自由度无机械阻尼俯仰自由振荡方程可写为
(11)
式中:I为无量纲化的转动惯量,通过数值计算得到自由俯仰振荡的时间历程曲线θ=θ(t)和Cm=Cm(t)后,可确定自由振荡的频率f=1/T,并选取同一个周期的两个峰值解θ1、θ2,可进而得到平衡迎角处的动导数:
(12)
上述方法只能辨识出平衡迎角处的动导数,应用受到一定的限制。袁先旭[14]提出了一种新型振荡法,可辨识出自由振荡经过的任一迎角处的动导数,拓宽了该方法的应用范围。
最近几年,求解周期性非定常流场的谐波法等方法得到了快速发展,并被应用于动导数的预测[15-17]。由于不需要求解一个完整的振荡周期,计算效率有大幅提高,但其本质仍可归类为强迫振荡法,这里不再展开叙述。
上述方法均以俯仰为例,给出俯仰动导数的辨识过程,偏航和滚转的动导数可类似给出。另外,上述方法得到的是组合导数,要将组合项分离开,则需加入平动运动的模拟,具体方法可参阅文献[18]。综合以上方法不难看出,数值模拟预测动导数的方法,其过程中存在一些共同的问题:首先,需要求解非定常Navier-Stokes方程,一般采用双时间步方法,时间步长的选取、子迭代步数以及子迭代收敛判据等都会影响辨识结果;其次,如果是自由振荡,则需要给定飞行器的转动惯量,而如果是强迫振荡,则需要给定飞行器的振荡频率,不同的振荡频率和振荡幅值也会影响动导数的辨识结果;最后,复杂构型飞行器存在流动干扰,也会影响动导数的预测精准度,而交叉导数和交叉耦合导数的辨识方法目前还存在争议。对以上这些问题,本文将结合算例进行具体分析。
3 动导数预测中存在的问题与分析
3.1时间步长、子迭代步数的选取
对飞行力学方程和Navier-Stokes方程之间的耦合求解问题,通常有松耦合和紧耦合之分。松耦合方法将飞行力学方程和Navier-Stokes方程分别独立求解,在时间域上交错推进,从而获得耦合系统的响应。已经证明,该方法在时间推进上只有一阶精度,过大的时间步长将显著降低非定常流场求解精度,进而降低动导数的预测精度。紧耦合方法[19]在亚迭代中实现两套系统之间的信息交换,耦合推进的时间精度能达到二阶,因而对时间步长的选取可比松耦合方法稍大。
以松耦合方法为例,分析时间步长、子迭代步数对动导数预测结果的影响。选取的计算模型为钝度比为0.3的钝锥,其外形和网格如图1所示。来流马赫数Ma∞=6.85,以底部直径为参考长度的雷诺数Re=1.45×106,强迫振荡的振幅为1°。

图1 钝锥外形和计算网格Fig.1 Geometry and computational grid of blunt cone
表1给出了模拟结果,无量纲时间步长分别取为0.10,0.05,0.20;子迭代步数分别取为6,15,25。时间步长和子迭代步数的选取对静导数影响较小,但对动导数的影响很大。同样的时间步长,随着子迭代步数的增加,动导数预测结果有向试验数据逼近的趋势;同样的子迭代步数,随着时间步长的降低,动导数预测结果同样有向试验数据逼近的趋势。
表1的计算结果似乎表明,时间步长越小越好、子迭代步数越多越好;而当时间步长、子迭代步数满足了一定的收敛性要求后,动导数的预测结果与两者的选取是无关的。因此,认为要保证动导数的预测精准度,时间步长和子迭代步数必须满足亚迭代收敛性的要求,以降低数值误差。建议在计算过程中,检验并给出亚迭代收敛曲线。
表1时间步长、子迭代步数等对预测结果的影响
Table 1Effect of time step, step number of sub-iteration, etc. on prediction result

TimestepSubiterationstepnumberStaticderivativesDynamicderivatives0.106-0.058454-0.48250215-0.057769-0.27530325-0.057594-0.2009810.056-0.057845-0.30687815-0.057663-0.14117525-0.057607-0.1322060.026-0.057630-0.12471115-0.057576-0.11344825-0.057566-0.107140Experiment[18]-0.1056±0.0158
3.2振荡频率的影响
飞行器在实际飞行时,燃料的持续消耗将会导致飞行器的转动惯量发生改变;飞行高度的变化则会改变来流密度;在阵风等扰动的持续作用下,飞行器的受迫振荡等,这些因素都会导致实际飞行时飞行器的振荡频率不断地变化,因而需要考察动导数随频率的变化关系。
针对超声速带翼导弹标模外形,研究了动导数预测结果随频率的变化问题。计算模型和网格如图2所示。

图2 带翼导弹标模外形和网格Fig.2 Basic finner geometry and grid
采用谐波平衡法和双时间步方法预测了飞行器的动导数,计算结果如图3所示。其中“DTS”为双时间步方法的计算结果,“Exp”为试验结果[20],“1 Harmonic”表示谐波数取1时,谐波平衡点的动导数预测结果。图3的计算结果表明,一般情况下,两种方法的预测结果均与试验值吻合良好。
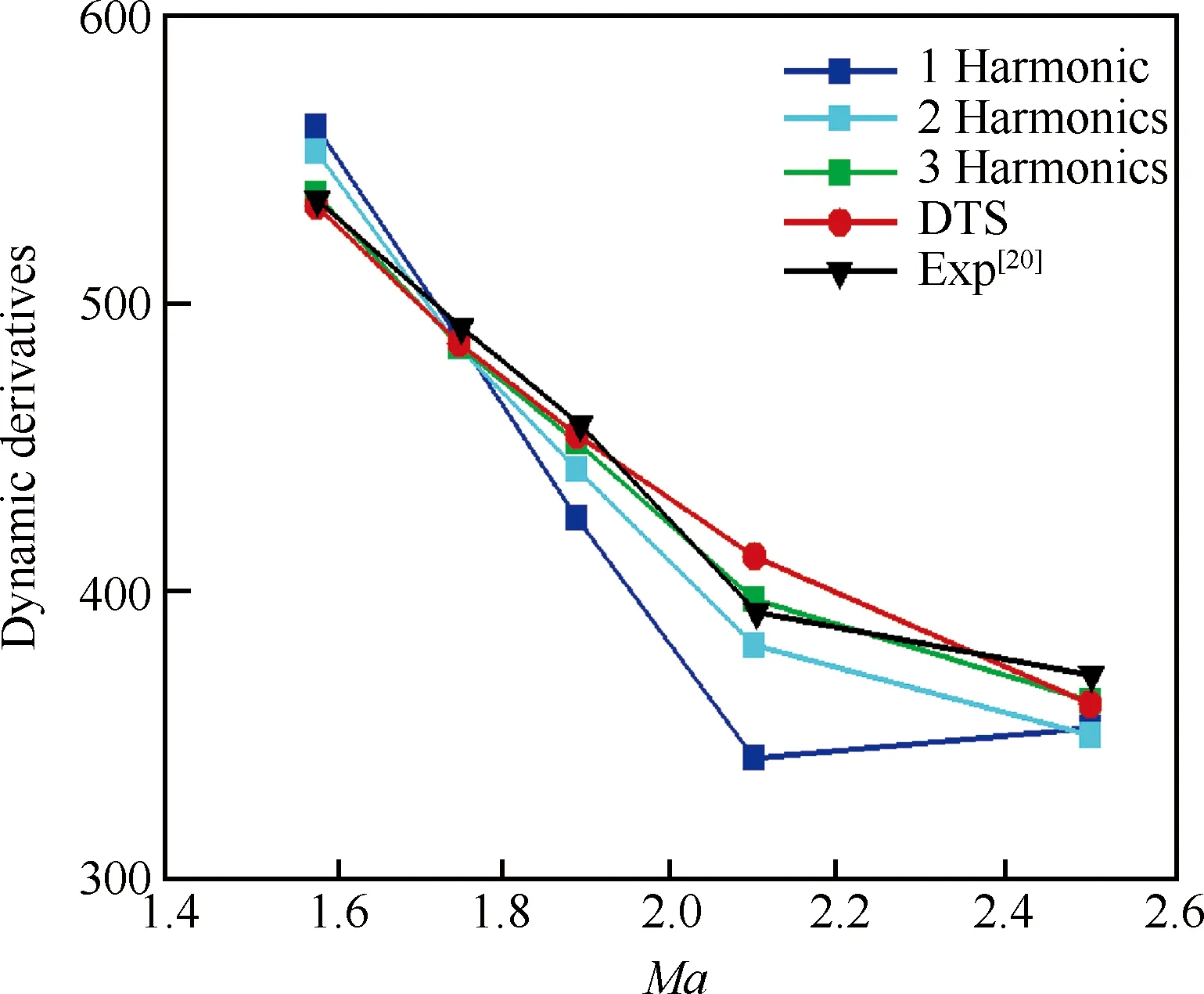
图3 动导数预测结果与试验值比较Fig.3 Comparison between dynamic derivative prediction results and experimental data
图4则是不同频率时的动导数预测结果,图中k为无量纲减缩频率。从预测结果来看,对超声速飞行器,在频率较大时,动导数对频率的变化不敏感,这符合以往的经验认识。在实际应用时,也常常选取较大的振荡频率,以提高动导数的预测效率。但在低频时,动导数随振荡频率的降低迅速发生改变。若飞行器的固有振荡频率较低,而计算时选取的频率较高,则预测结果可能会背离真实情况。

图4 频率对动导数预测结果的影响 Fig.4 Effect of frequency on dynamic derivativeprediction results
孙涛等[21]针对相同的外形,研究了振荡频率f的影响,也给出了相似的研究结论(见图5)。
而对类航天飞机外形的飞行器,在研究其俯仰动导数时发现(见图6):在低空低马赫数时,不同频率的预测结果差别不大;但高空高马赫数时,不同频率的结果差别明显。

图5 频率对动导数预测结果的影响[21]Fig.5 Effect of frequency on dynamic derivativeprediction results[21]
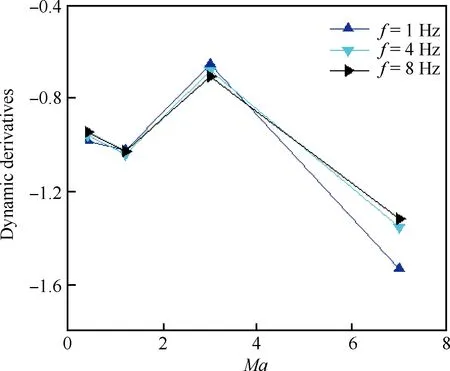
图6 不同频率时动导数预测结果随马赫数的变化Fig.6 Dynamic derivative prediction results versusMach number at different frequencies
在以往的研究任务中,基于“动导数随频率变化不大”的经验认识,或者在不清楚飞行器振荡频率时,通常会选取较大的振荡频率,一般给定f=2~10 Hz,以提高非定常计算效率。但理论分析[14]和实践表明,振荡频率不能随意给定。建议结合飞行器的典型飞行状态、质量特性和静导数,估算给出典型振荡频率。
3.3自由振荡与强迫振荡的预测结果差异
通常情况下,自由振荡方法和强迫振荡方法的动导数预测结果互为补充,可以相互验证。以构型较为简单平头双锥带翼飞行器外形(见图7)为例,采用强迫振荡法获取了不同马赫数时的动导数,如图8所示。

图7 平头双锥外形示意图 Fig.7 Schematic diagram of flat-nose wingeddouble-cone body

图8 平头双锥外形不同马赫数时的动导数Fig.8 Dynamic derivatives at different Mach numbers for flat-nose winged double-cone body
从模拟结果来看,随着马赫数的增加,俯仰动导数的量值逐渐减小,表明飞行器受到的气动阻尼不断降低;最后在Ma=7.0时,动导数的符号也发生了变化(α=0°),此时空气对飞行器做正功,飞行器的自由振荡将可能发散。
图9则通过模拟自由振荡的过程,得到了不同马赫数时俯仰角的时间历程曲线,起始迎角α1分别为1° 和4°。可以看到,低马赫数时,俯仰角是收敛的,但随着马赫数增大,气动阻尼降低,俯仰角收敛的速度越来越慢;在Ma=7.0时,动导数为正值,此时俯仰角的振荡幅值不断增加。自由振荡结果验证了图8的强迫振荡动导数预测结果。

图9 自由振荡模拟得到的俯仰角时间历程曲线Fig.9 Time history curves of pitch angle from free oscillation simulation
但是对复杂构型的升力体外形(见图10),图11 给出了两种方法预测的动导数结果比较。同样的振荡频率下,两种方法得到的结果差别较大,在迎角大于10° 以后,两种方法给出的动导数符号都不一致。在另外一些飞行器的计算中,也发现相似的问题。
POD数据后处理应用程序包由数据输入模块、POD数据处理核心模块和数据输出模块等3个功能模块组成(见图1)。
从我们的计算经验来看,自由振荡法预测动导数时,由于需要人工选取同一个周期的两个峰值解θ1、θ2,选取的周期不同,特别是当θ1、θ2与平衡迎角距离较远时,不完全满足动导数邻域的概念,对动导数的辨识结果有较大影响。因此,建议尽量采用小振幅强迫振荡法预测动导数,以典型状态的自激振荡结果作为验证。

图10 升力体外形Fig.10 Geometry of lifting body

图11 升力体外形强迫振荡和自由振荡方法辨识的动导数的比较Fig.11 Comparison of dynamic derivatives for lifting body using forced and free oscillation methods
3.4交叉导数和交叉耦合导数的预测
以往,交叉导数和交叉耦合导数常常被认为是小量而被忽略,没有得到足够的重视。近年来,随着飞行器对机动性和敏捷性的要求越来越高,特别是在大迎角机动飞行时,交叉导数和交叉耦合导数的重要性日益凸显。

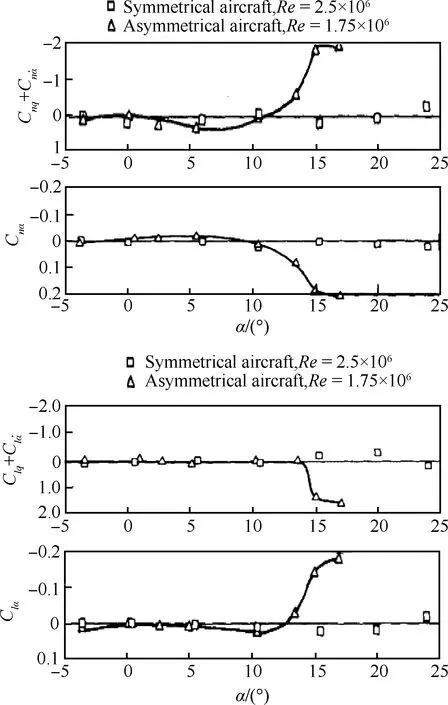
图12 交叉耦合导数随迎角的变化情况[22]Fig.12 Variation of cross coupling derivatives with angle of attack[22]

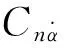
目前,交叉导数和交叉耦合导数仍沿用单自由度强迫振荡法,可能不能反应飞行器运动之间的耦合效应。建议结合控制系统设计要求设计典型耦合运动形式,并基于该运动形式的气动力矩时间历程曲线辨识交叉导数和交叉耦合导数。
不同外形特征的飞行器,其动态特性相差较大,特别是对内外流一体化飞行器外形,由于振荡时存在内外流干扰,其动态特性比常规飞行器更为复杂。此外,为确保进气道的正常启动,内外流一体化飞行器对姿态控制的精度要求更高,故其操纵性稳定性分析评估也更加重要,需要准确预测动导数。
对研究的某环形进气道外形的飞行器(图13是进气道入口附近的网格),在研究其俯仰动导数时发现:对常规纯外流飞行器通常在计算启动后一个振荡周期内即可进入迟滞圈,迟滞圈重复性较好;而内外流一体化飞行器的相轨线一般经过剧烈振荡才能形成迟滞圈,且迟滞圈重复性较差,如图14所示。
对另一型内外流一体化飞行器,考虑湍流模型和不考虑湍流模型的计算,两种动导数的预测结果甚至出现了反号(见图15)。这些现象都表明,内外流一体化飞行器振荡时,由于内外流相互作用和相互干扰,导致其动态特性也更为复杂,需要更深入地开展相关的研究工作。

图13 进气道入口附近形状和网格Fig.13 Geometry and grid near inlet

图14 内外流一体化飞行器迟滞圈Fig.14 Hysteresis loop for integrated internal-externalflow vehicle

图15 考虑和不考虑湍流模型时计算的动导数Fig.15 Comparison of dynamic derivatives with/without turbulence model
建议对于此类问题,应采用多种模型、多种方法进行对比分析,以保证动导数预测的精准度。
4 结 论
针对动导数数值预测中存在的问题、困难开展讨论,并结合具体算例进行分析。总体来看,出现问题的原因可大致归为两类:
1) 方法问题。包括数值计算方法和动导数辨识方法等。非定常计算的子迭代收敛判据、时间步长的选取、计算模型与计算方法的选取和计算网格设计等,都会对动导数预测结果产生影响。
2) 物理机制。包括动导数、交叉导数的概念和适用范围等。动导数的概念本质上属于线化小扰动理论范畴,在气动力非定常、非线性效应很强的时候,动导数的概念是否适用以及如何使用等问题仍是未解的难题。
3) 针对数值预测动导数中存在的各种问题,结合我们自己的研究经验,提出了一些意见和建议,供参考。
[1]刘绪. 高超声速内外流一体化飞行器动态特性研究[D]. 长沙: 国防科学技术大学, 2011: 1-3.
LIU X. Investigation of dynamic characteristics of hypersonic airframe/propulsion integrative vehicle[D]. Changsha: National University of Defense Technology, 2011: 1-3 (in Chinese).
[2]WEINACHT P. Navier-Stokes predictions of pitch damping for a family of flared projectiles: AIAA-1991-3339[R]. Reston: AIAA, 1991.
[3]QIN N, LUDLOW D K, SHAW S T, et al. Calculation of pitch damping coefficients for projectiles: AIAA-1997-0405[R]. Reston: AIAA, 1997.
[4]刘伟, 张鲁民. 钝体俯仰阻尼导数数值计算[J]. 空气动力学学报, 1997, 15(4): 427-435.
LIU W, ZHANG L M. Numerical calculation of damping in pitch derivatives of blunt cone[J]. Acta Aerodynamics Sinica, 1997, 15(4): 427-435 (in Chinese).
[5]刘伟, 牟斌. 高超声速滚转阻尼导数数值模拟[J]. 飞行力学, 2000, 18(2): 27-29.
LIU W, MOU B. Numerical simulation of damping-in-roll derivatives of blunt cone for hypersonic flow[J]. Flight Dynamics, 2000, 18(2): 27-29 (in Chinese).
[6]刘伟, 刘君, 柳军. 平衡气体效应对飞行器动态特性的影响研究[J]. 飞行力学, 2004, 22(4): 65-68.
LIU W, LIU J, LIU J. Investigation of equilibrium gas effect on dynamic characteristic of aerocraft[J]. Flight Dynamics, 2004, 22(4): 65-68 (in Chinese).
[7]袁先旭, 张涵信, 谢昱飞. 基于CFD 方法的俯仰静、动导数数值计算[J]. 空气动力学学报, 2005, 23(4): 458-463.
YUAN X X, ZHANG H X, XIE Y F. The pitching static/dynamic derivatives computation based on CFD methods[J]. Acta Aerodynamics Sinica, 2005, 23(4): 458-463 (in Chinese).
[8]袁先旭, 陈坚强, 王文正. 平头增阻再入体俯仰动态特性计算与流动机理分析[J]. 空气动力学学报, 2007, 25(3): 300-305.
YUAN X X, CHEN J Q, WANG W Z. Pitching dynamic stability computation for plane nose reentry vehicle and flow mechanism analysis[J]. Acta Aerodynamics Sinica, 2007, 25(3): 300-305 (in Chinese).
[9]袁先旭, 张涵信, 谢昱飞. 飞船返回舱再入俯仰动稳定吸引子数值仿真[J]. 空气动力学学报, 2007, 25(4): 431-436.
YUAN X X, ZHANG H X, XIE Y F. Numerical simulation for dynamic stability in pitching of unfinned reentry capsule and bifurcation with mach number prediction[J]. Acta Aerodynamics Sinica, 2007, 25(4): 431-436 (in Chinese).
[10]BRYAN G, WILLIAMS W. The longitudinal stability of aerial gliders[J]. Proceedings of the Royal Society of London, 1904, 73(488-496): 100-116.
[11]TOBAK M, SCHIFF L B. On the formulation of the aerodynamic characteristics in aircraft dynamics: NASA technical report, N76-15082/OSL[R]. Washington, D.C.: NASA, 1976.
[12]ETKIN B, TEICHMANN T. Dynamics of flight: Stability and control[J]. Journal of Guidance Control & Dynamics, 2009, 20(4): 839-840.
[13]任玉新, 刘秋生. 飞行器动态稳定性参数的数值计算方法[J]. 空气动力学学报, 1996, 14(2): 117-126.
REN Y X, LIU Q S. A numerical method for evaluating aerodynamic stability parameters of vehicles[J]. Acta Aerodynamica Sinica, 1996, 14(2): 117-126 (in Chinese).
[14]袁先旭. 非定常流动数值模拟及飞行器动态特性分析研究[D]. 绵阳: 中国空气动力研究与发展中心, 2002: 111-115.
YUAN X X. Numerical simulation for unsteady flows and research on dynamic characteristics of vehicle[D]. Mianyang: China Aerodynamics Research and Development Center, 2002: 111-115 (in Chinese).
[15]陈坚强, 陈琦, 袁先旭, 等. 舵面操纵动态响应的数值模拟研究[J]. 力学学报, 2013, 45(2): 302-306.
CHEN J Q, CHEN Q, YUAN X X, et al. Numerical simulation study on dynamics response under rudder control[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 302-306 (in Chinese).
[16]陈琦, 陈坚强, 袁先旭, 等. 谐波平衡法在动导数快速预测中的应用研究[J]. 力学学报, 2014, 46(2): 183-190.
CHEN Q, CHEN J Q, YUAN X X, et al. Application of a harmonic balance method in rapid predictions of dynamic stability derivatives[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 183-190 (in Chinese).
[17]杨小权, 程苏堃, 杨爱明, 等. 基于时间谱方法的振荡翼型和机翼非定常黏性绕流数值模拟[J]. 航空学报, 2013, 34(4): 787-797.
YANG X Q, CHENG S K, YANG A M, et al. Time spectral method for numerical simulation of unsteady viscous flow over oscillating airfoil and wing[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4): 787-797 (in Chinese).
[18]刘伟, 杨小亮, 赵云飞. 高超声速飞行器加速度导数数值模拟[J]. 空气动力学学报, 2010, 28(4): 426-429.
LIU W, YANG X L, ZHAO Y F. Numerical simulation of acceleration derivative of hypersonic aircraft[J]. Acta Aerodynamics Sinica, 2010, 28(4): 426-429 (in Chinese).
[19]杨云军, 崔尔杰, 周伟江. 细长三角翼滚转/侧滑耦合运动的数值研究[J]. 航空学报, 2007, 28(1): 14-19.
YANG Y J, CUI E J, ZHOU W J. Numerical research on roll and sideslip coupling motions about a slender delta-wing[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 14-19 (in Chinese).
[20]EAST R A, HUTT G R. Comparison of predictions and experimental data for hypersonic pitching motion stability[J]. Journal of Spacecraft and Rockets, 1988, 25(3): 225-233.
[21]孙涛, 高正红, 黄江涛. 基于CFD的动导数计算与减缩频率影响分析[J]. 飞行力学, 2011, 29(4): 15-18.
SUN T, GAO Z H, HUANG J T. Identify of aircraft dynamic derivatives based on CFD technology and analysis of reduce frequency[J]. Flight Dynamics, 2011, 29(4):15-18 (in Chinese).
[22]COULTER S M, MARQUART E J. Cross and cross-coupling derivative measurements on the standard dynamics model at AEDC: AIAA-1982-0596[R]. Reston: AIAA, 1982.
[23]BUTLER R W. Aircraft motion sensitivity to cross and cross-coupling damping derivatives: NASA technical report, AD-A032 654/6SL[R]. Washington, D.C.: NASA, 1977.
[24]BUTLER R W, LANGHAM T F. Sensitivity of aircraft spinning motion to dynamic cross-coupling and acceleration derivatives: NASA technical report, AD-A060 516/2SL[R]. Washington, D.C.: NASA, 1979.
[25]LANGHAM T F. Aircraft motion sensitivity to dynamic stability derivatives: AIAA-1979-1621[R]. Reston: AIAA, 1979.
[26]何植岱. 飞机大迎角稳定性对于交叉导数和加速度导数的灵敏度分析[J]. 空气动力学学报, 1987, 5(4): 334-344.
HE Z D. Sensitivity of aircraft stability to cross-coupling derivatives and angular acceleration derivatives at high angles of attack[J]. Acta Aerodynamics Sinica, 1987, 5(4): 334-344 (in Chinese).
袁先旭男, 博士, 研究员。主要研究方向: 非定常流动数值模拟、 飞行器动态特性分析、 复杂流动数值计算方法等。
Tel: 0816-2463168
E-mail: yuanxianxu@cardc.cn
陈琦男, 博士, 助理研究员。主要研究方向: 非定常流动数值模拟、 飞行动态特性分析、 计算软件开发等。
Tel: 0816-2463304
E-mail: chenqi@mail.ustc.edu.cn
谢昱飞男, 博士, 副研究员。主要研究方向: 非定常流动数值模拟、 飞行动态特性分析等。
Tel: 0816-2463090
E-mail: xyf_5843@qq.com
Problems in numerical prediction of dynamic stability derivatives
YUAN Xianxu, CHEN Qi, XIE Yufei*, CHEN Jianqiang
Computational Aerodynamics Institute, China Aerodynamics Research and Development Center,Mianyang621000, China
Dynamic stability derivative is one of the important parameters in the design of control system, the design of flight orbit, and the analysis of dynamic stability of vehicles. The prediction methods of the dynamic stability derivatives mainly include the engineering approximations, numerical simulations and wind tunnel tests. The concepts of dynamic stability derivative and cross derivative are reviewed, and the forced oscillation and free oscillation methods for numerically predicting the dynamic stability derivatives are introduced. The problems existing in the numerical prediction are specially discussed, including the choice of time-marching step and step number of sub-iteration, the effects of the oscillating frequency on the identification results, the analysis of the probable reasons which lead to the difference between the forced oscillation and free oscillation methods in dynamic derivative identification, the identification of the cross and cross coupling derivatives, and the identification of dynamic stability derivatives of the integrated internal-external flow vehicles. The discussions are made with computational cases and detailed analysis, in which both experiences and puzzles exist, and the corresponding suggestions for improvement are presented.
dynamic derivative; cross derivative; forced oscillation; free oscillation; oscillating frequency
2016-04-21; Revised: 2016-04-29; Accepted: 2016-06-04; Published online: 2016-06-1209:01
s: National Natural Science Foundation of China (11172315, 11372341, 11532016)
. Tel.: 0816-2463090E-mail: xyf_5843@qq.com
2016-04-21; 退修日期: 2016-04-29; 录用日期: 2016-06-04;
时间: 2016-06-1209:01
www.cnki.net/kcms/detail/11.1929.V.20160612.0901.002.html
国家自然科学基金 (11172315, 11372341, 11532016)
.Tel.: 0816-2463090E-mail: xyf_5843@qq.com
10.7527/S1000-6893.2016.0180
V211.3
A
1000-6893(2016)08-2385-10
引用格式: 袁先旭, 陈琦, 谢昱飞, 等. 动导数数值预测中的相关问题[J]. 航空学报, 2016, 37(8): 2385-2394. YUAN X X, CHEN Q, XIE Y F, et al. Problems in numerical prediction of dynamic stability derivatives[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2385-2394.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
URL: www.cnki.net/kcms/detail/11.1929.V.20160612.0901.002.html
