桥面栏杆对主梁气动力和涡脱特性的影响研究

祝志文

(1.湖南大学 土木工程学院,湖南 长沙 410082;2.湖南大学 风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082)



桥面栏杆对主梁气动力和涡脱特性的影响研究

祝志文1,2

(1.湖南大学 土木工程学院,湖南 长沙 410082;2.湖南大学 风工程与桥梁工程湖南省重点实验室,湖南 长沙 410082)

为研究桥面栏杆对桥梁主梁气动特性的影响，分别开展大带东桥主桥加劲梁施工和成桥阶段的CFD模拟，获得不同来流攻角下加劲梁的气动力系数、表面平均压力系数分布和漩涡脱落Strouhal(St)数，并与文献结果进行比较。研究结果表明：栏杆钝化了加劲梁气动特性，局部改变了加劲梁迎风侧压力分布，并使成桥阶段加劲梁阻力系数明显大于施工阶段，0o攻角增大38%。施工和成桥阶段加劲梁均呈现多阶涡脱特征，施工阶段高阶涡脱峰值占优且不受时间步细化的影响；成桥阶段当时间步足够小后可给出峰值占优的低阶涡脱。研究认为，传统CFD模拟忽略桥面附属设施研究成桥气动特性的做法需要改变，必须重视桥面栏杆的抗风设计，重视施工和成桥阶段主梁不同的多阶涡脱特性。

大跨度桥梁；气动力；漩涡脱落；桥面栏杆；湍流模型

大跨度桥梁结构模态频率和阻尼比低，容易产生因漩涡脱落而导致的涡激振动。国内外已报道了多座大跨度桥梁多阶模态涡激共振现象[1,2]。通常认为多阶涡激的主要影响因素有桥梁主梁St数、结构模态频率和阻尼，以及桥址风场特性等。一般认为，成桥主梁对应单一St数[3]，其值在0.08～0.15之间，且不受结构模态频率的影响[4]。然而，从实际三维桥梁主梁和流体漩涡的三维特性，以及漩涡运动的非定常与沿展向产生、脱落和漂移的不同步[5]来看，桥梁主梁涡脱可能表现出多阶涡脱和多St数特征。且因施工和成桥阶段主梁气动外形不同，也可能存在不同的多阶涡脱特征。考虑到栏杆的挡风面积可能远小于桥梁主梁，传统CFD模拟获取成桥阶段主梁气动特性和颤振特性，往往忽略桥面附属设施，将成桥阶段主梁简化成没有桥面附属设置，如栏杆、防撞栏、检修道等的裸梁，这实际对应为桥梁主梁施工阶段[6-8]。由于主梁气动特性可能受气动外形细微改变的影响，可能导致主梁静气动力系数和动气动参数的明显变化，从而可能影响桥梁抗风性能的评价，甚至可能带来不安全的因素。这种简化处理需要改变，然而系统地开展桥面附属设施对主梁气动特性，特别是多阶涡脱的影响，未见相关研究报道。基于上述考虑，本文以丹麦大带东桥加劲梁为研究对象，开展不同来流攻角下施工和成桥阶段加劲梁CFD模拟，获得桥面栏杆和裸梁的气动力系数，以及主梁表面平均压力分布和涡脱St数。本文试图基于CFD模拟，探讨栏杆对主梁气动特性和多阶涡脱的影响。

1　流动控制方程

桥梁风工程绕流属于不可压粘性流动，其雷诺时均Navier-Stokes方程可表示为：

(1)

(2)

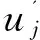
(3)

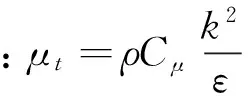
(4)

(5)

其中：Cε1和Cε2为模型常数；σk和σε分别是k和ε的湍流Prandtl数。

标准k-ε模型是一种高雷诺数湍流模型，适合于充分发展的湍流求解。对风工程中钝体的复杂流动问题，该模型往往高估流动的湍动能，并在逆压梯度区通常给出明显偏大的湍流积分尺度，因而目前很少单独采用标准k-ε模型研究风工程问题。如果定义μt=k/ω为湍流黏性；ω=ε/k为湍流耗散率和湍动能的比，适应于低雷诺数流动的k-ω湍流模型方程表示为：

(6)

(7)

对低Re流动，该模型需要通过提供足够的网格分辨率直接求解。结合标准k-ε模型和k-ω湍流模型各自的优缺点，Menter提出了一种SST (Shear Stress Transport) k-ω模型[9]。该模型将SST k-ω模型方程和标准k-ε模型方程分别乘以混合函数Fl和(1-Fl)，设定近壁区内Fl取值1，使得近壁区的流动采用SST k-ω模型模拟，而在近壁区以外Fl为0，从而过度到标准k-ε模型。如此处理，SST k-ω湍流模型能获得优于标准k-ε模型和SST k-ω模型的模拟结果。

2　研究对象和数值实现

在1999年6月24日召开的第10届国际风工程会议上成立了桥梁空气动力学执行委员会和CFD工作组，将丹麦大带东桥确定为CFD模拟的基准模型 (http://www.iawe.org)，用于检验所用CFD方法的有效性。多年来，丹麦大带东桥主桥加劲梁常作为桥梁抗风和CFD模拟的算例模型。该桥为主跨1 624 m的三跨连续钢箱梁悬索桥。加劲梁横断面全宽31 m，桥轴线处梁高4.4 m，断面宽高比为7.045，布置如图1所示。该桥在设计阶段开展了1∶80的节段模型风洞试验[10-11]。为与相关文献结果对比，本文CFD模拟采用与风洞实验一致的模型缩尺比和来流风速，对应流动Re=3.18×105。CFD计算分包含和不包含桥面两侧栏杆和中央防撞栏，即分别对应加劲梁的成桥和施工状态，不考虑主缆和吊杆对加劲梁气动力和涡脱特性的影响。

单位:m图1　加劲梁横断面和气动力定义Fig.1 Stiffening girder cross section and definition of aerodynamic forces

2.1计算域网格及流动条件

CFD模拟的计算域如图2所示。为减小边界的反射效应，计算域入口、上侧和下侧边界到加劲梁断面剪切中心(Shear center, S.C.)的距离均为13B，对应的模型堵塞度为0.5%，满足风工程模拟对模型堵塞度的要求。为减小下游边界对计算域流动的影响，下游出口到S.C.的距离为26B。采用计算域分区划分网格以控制网格的正交性和网格缩放比。加劲梁断面外的计算域Z1为椭圆形，网格的布置主要考虑流动变量在其上的分布变化，以及相邻域间网格尺寸的协调处理。Z2外为椭圆边界；Z3和Z4区域外边界均为圆；Z5，Z6和Z7区域的网格布置主要用于网格尺度和质量的控制，以保持尾流区网格较高分辨率。

计算域边界条件为：计算域入口边界定义为水平均匀速度边界，湍流度为0；下游出口施加流动出口边界条件；加劲梁表面使用无滑移壁面条件；计算域上、下边界采用对称边界条件。初始场采用入口速度初始化。数值计算采用SST k-ω湍流模型和非定常二阶隐式格式，采用速度-压力解耦的SIMPLE算法，二阶格式离散压力方程，动量、湍动能和湍流耗散率方程均采用二阶迎风格式。通过监视气动力时程，当加劲梁上作用的气动力收敛后开始采集气动力数据，所有数值模拟均基于CFD专用程序Fluent 6.3.26开展。

2.2时间步无关和网格无关检查

分别定义模型断面气动升力、阻力和扭矩系数为：

(8)其中：U0为计算域入口风速；FL，FD和M分别为作用在加劲梁或全部栏杆上的阻力、升力和扭矩(正方向定义见图1)；B和H分别为加劲梁模型宽度和高度。

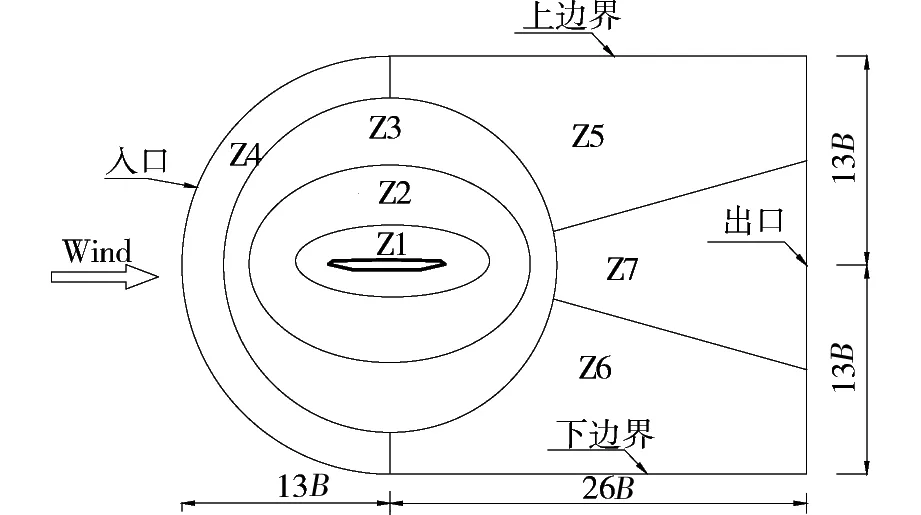
图2　计算域网格划分分区Fig.2 Schematic plot of computational domain partition around girder

图3　施工阶段加劲梁周围网格Fig.3 Mesh around girder in construction stage

定义漩涡脱落St数：

St=fsH/U0

(9)

式中：fs为漩涡脱落频率，Hz。

本文先以加劲梁无桥面栏杆的施工状态，采用如表1所示的具有不同物面第1层网格高度的3套网格，其中网格2如图3所示。以EquiAngle Skew值度量网格质量，3套网格在优良(excellent)以上(0～0.25)的网格数量占总数量的97%，而100%网格质量为好(Good，0.25～0.5)。

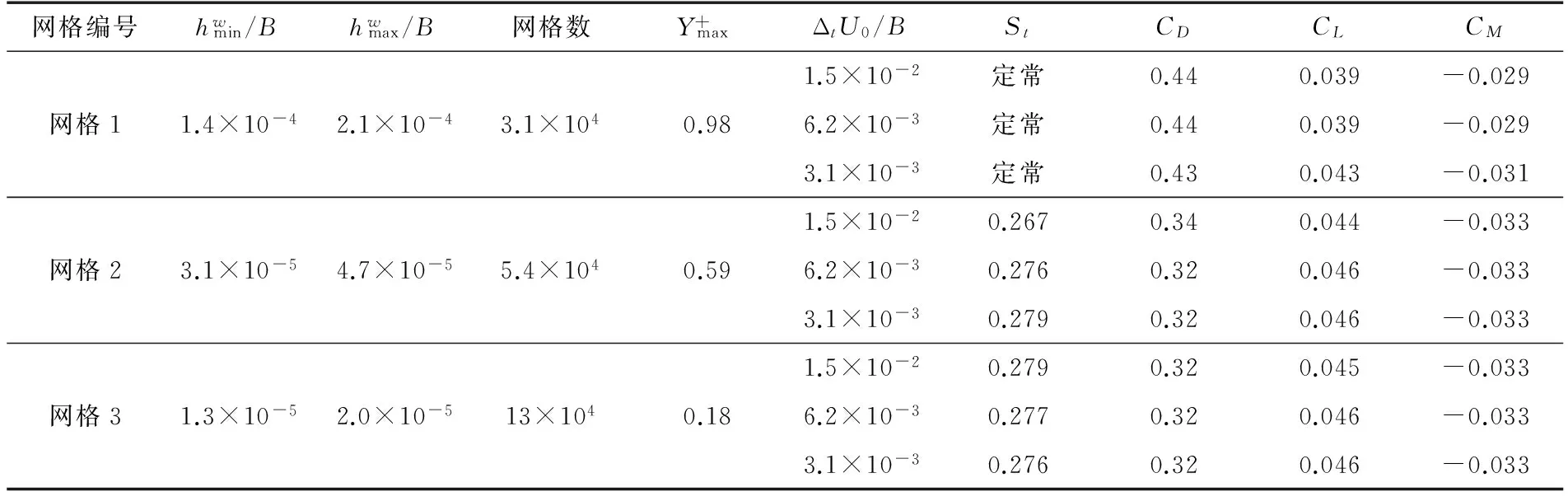
表1　不同网格系统的计算结果Table 1 Flow results on different grid system

表1为不同网格系统在3个时间步长上的计算结果。可见，网格1的力系数值均与网格2和网格3有较大的偏差。虽然网格3物面法向网格分辨率明显提高，但气动力系数平均值，在3个时间步上结果均与网格2差别小。因而可认为网格2已获得了与网格无关的CFD结果，故确定网格2为施工阶段CFD计算网格。对网格2，在无量纲时间步长6.2×10-3和3.1×10-3上三分力系数和St数差别极小，可认为，当时间步长为6.2×10-3时，已获得与时间步无关的计算结果。

3　施工和成桥阶段静气动力系数

为获得成桥阶段加劲梁气动特性，在施工阶段主梁上添加两侧和中央防撞栏。基本维持施工阶段网格2布置，特别是相同的物面及法向单元尺度；同时在栏杆表面和法向采用较高的网格分辨率，通过网格生长率控制使得栏杆周围网格向周围特别是桥面的平顺过渡。图4为成桥阶段绕主梁的网格布置以及栏杆区网格放大。图5是0°攻角下施工和成桥阶段加劲梁表面Y+分布，可见加劲梁表面网格分辨率满足SSTk-ω模型对网格的要求。

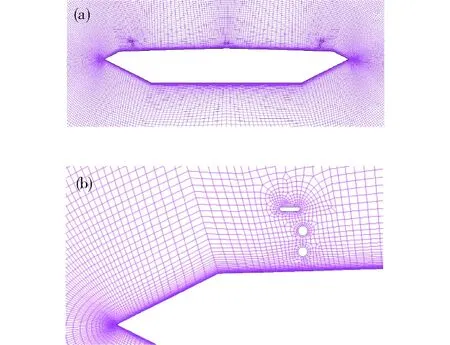
(a) 加劲梁周围；(b) 前缘和栏杆周围网格图4　加劲梁周围网格布置Fig.4 Grids arrangement around stiffening girder

为评价小尺度栏杆构件引入后时间步大小对成桥气动特性计算的影响，0°攻角进行了7个不同时间步上的CFD计算，如图6所示。可见栏杆和梁体的平均气动力系数基本没有变化，也即采用较大的时间步长就能获得成桥加劲梁的静气动力系数。

(a) 施工;(b) 成桥图5　加劲梁表面Y+分布Fig.5 Wall Y+ value on girder surface

图6　成桥阶段栏杆和梁体气动力系数Fig.6 Aerodynamic coefficients of deck rails and bare girder in in-service stage

图7～8分别是0°和无量纲时间步长为6.2×10-3时，施工阶段加劲梁与成桥阶段栏杆和裸梁的气动力系数时程。可见气动力已经收敛，且成桥裸梁和施工阶段加劲梁的力系数差别很小。图9是2阶段阻力系数随来流攻角的变化，并与节段模型风洞试验结果[11]进行了对比。因成桥阶段加劲梁模型与风洞试验外形一致，本文得到的0o攻角阻力系数为0.54，风洞试验值为0.57[11]，相对误差为5%。随着来流攻角绝对值的增大，阻力系数也不断增大，阻力系数曲线趋势呈内凹形，这也与一般桥梁主梁阻力系数的变化趋势相同。

图9中将成桥加劲梁的阻力系数分解成2个部分，一部分来自桥面防撞栏(即成桥栏杆，阻力系数同样采用式(5)无量纲化)，另一部分来自扣除防撞栏的主梁(即成桥裸梁)。可见成桥裸梁的阻力系数曲线与施工阶段基本一致，说明桥面栏杆的出现并没有明显改变加劲梁梁体的阻力系数。需要指出，栏杆的阻力系数在0.2左右，且没有表现出随攻角的明显变化。这样，可将成桥阶段加劲梁阻力系数曲线理解成是施工阶段阻力系数曲线向上平移栏杆阻力系数值。图10是在不同攻角下，成桥栏杆和裸梁的阻力贡献率。可见0o攻角时，栏杆阻力对整个加劲梁阻力的贡献达到38%，而随着攻角绝对值的增大，栏杆对阻力的贡献虽逐渐减小，但在最小贡献的±10°风攻角，其贡献率也达到22%。实际上，从栏杆的挡风面积来看，0o风攻角时仅占到成桥加劲梁挡风面积的9.5%，可见桥面栏杆显著钝化了此类扁平箱型的气动外形，因而需要重视栏杆的气动外形设计。

图11为施工和成桥阶段绕加劲梁的流线。可见桥面栏杆的出现强烈干扰了顶板上部流动。与施工阶段相比，顶板上部流动偏离桥面，造成了较宽的尾迹，由于高Re数流动的阻力以压差为主，必然导致成桥加劲梁阻力大于施工阶段。

图12～13分别为升力和扭矩系数随来流攻角的变化，0°攻角风洞试验分别为-0.05和-0.028[11]，可见成桥结果与风洞试验吻合较好。栏杆

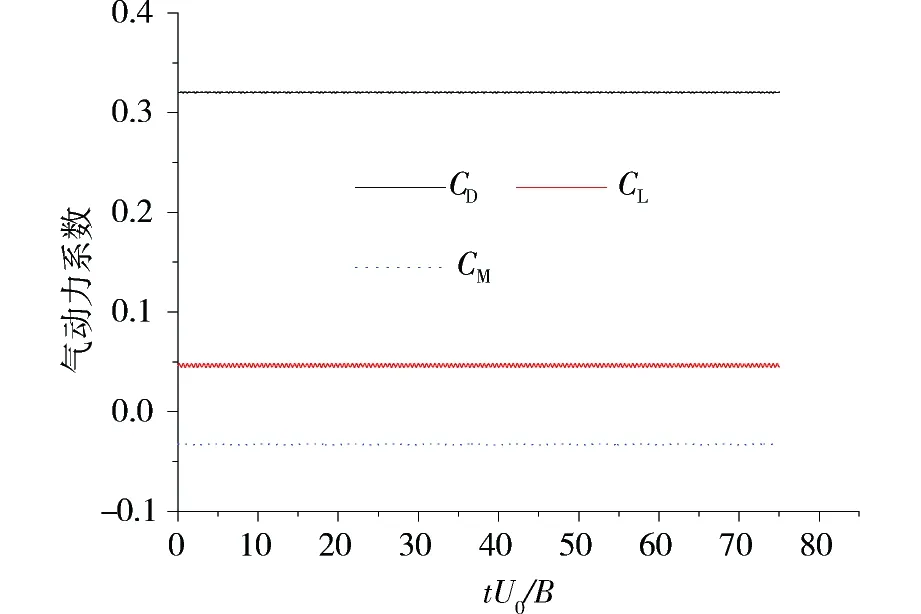
图7　施工阶段加劲梁气动力系数时程Fig.7 Force coefficient records of girder in construction stage

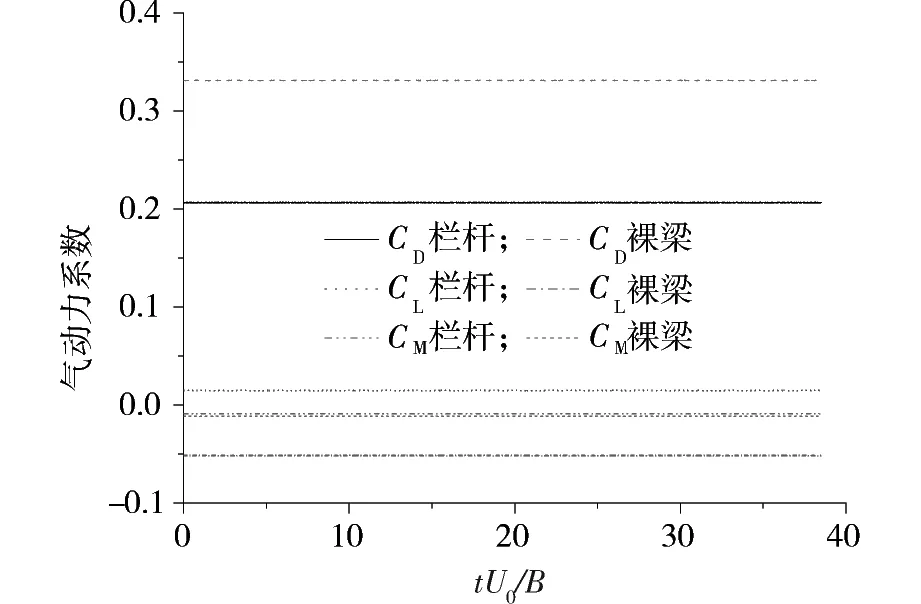
图8　成桥阶段裸梁和栏杆气动力系数时程Fig.8 Force coefficient records of bare girder and deck rails in in-service stage

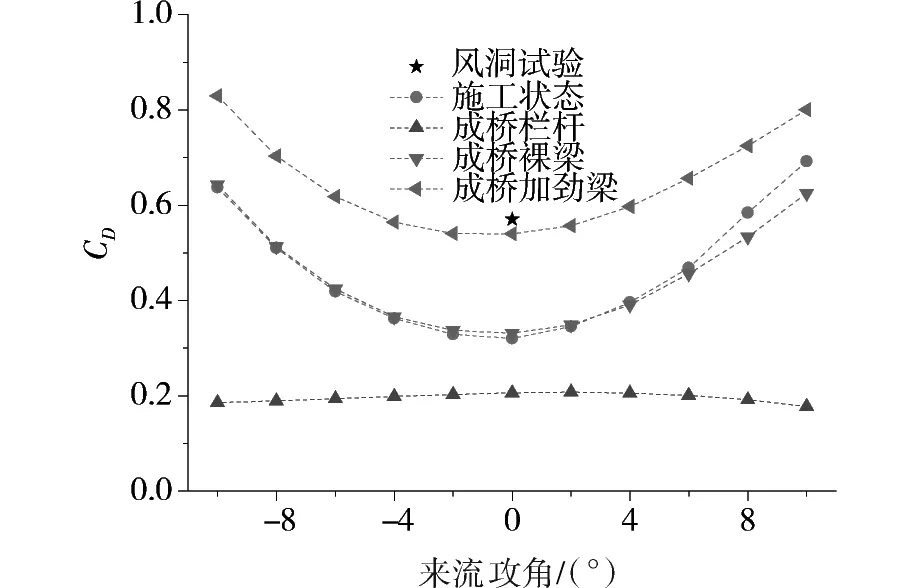
图9　阻力系数随来流攻角的变化Fig.9 Drag coefficients against wind angles of attack

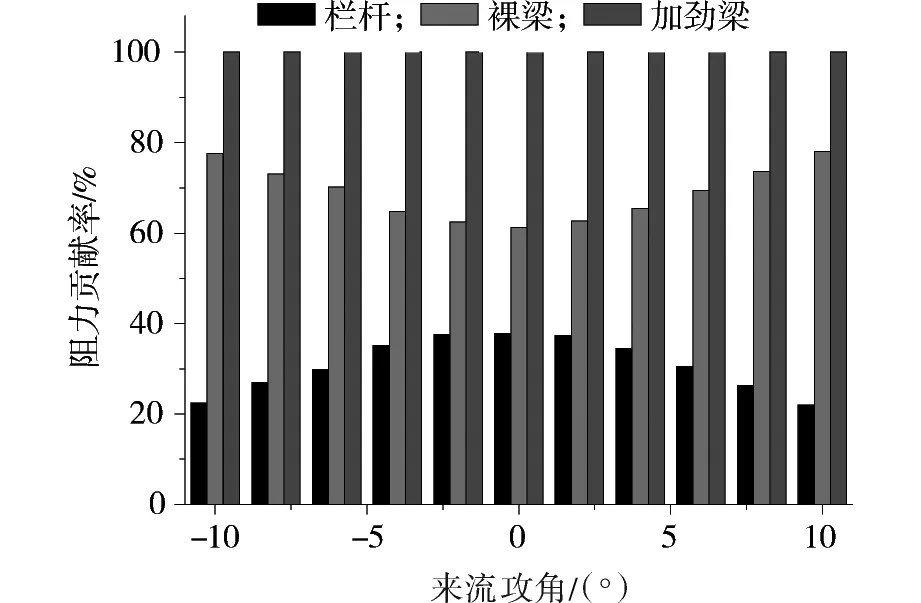
图10　栏杆和裸梁的阻力贡献率Fig.10 Drag contribution of deck rails and bare girder

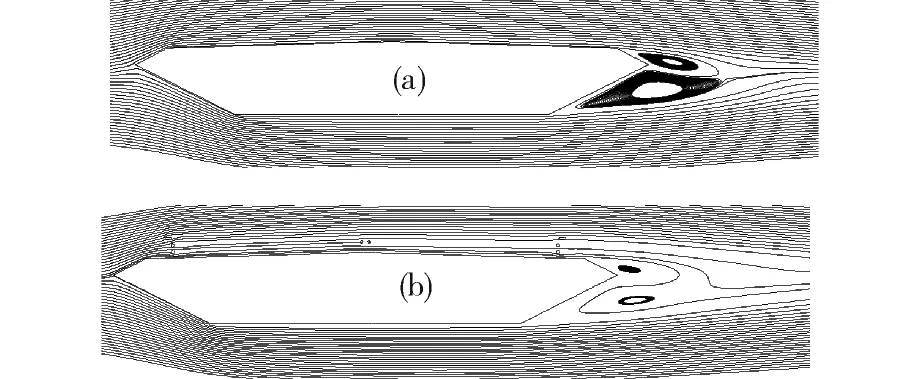
(a) 施工阶段;(b) 成桥阶段图11　绕主梁流线Fig.11 Streamlines around bridge girder

的出现也并没有明显改变梁体的升力特性，但由于栏杆本身升力的出现，使得成桥加劲梁升力与施工阶段出现了较小的差别，这个差别随着来流攻角的增大而增大，这可能是由于两侧栏杆最上部平板形细节的气动外形所引起。另外，扭矩系数较小，且近似表现为随攻角增大而线性变化的特征。

4　施工和成桥主梁涡脱特性

4.1施工阶段

图14为3个不同时间步升力系数时程的涡脱St数分析，时间步明显小于获得稳定气动三分力系数必须值。可见绕施工阶段加劲梁流动的涡脱表现为多阶，低阶St数均为0.10，接近风洞试验结果，但峰值St数均为0.277，St数的排序也不随时间步减小而发生改变。本文在主梁后缘点向下游平移1B的尾迹中监测流动的竖向速度Vy时程，并基于PSD分析获得3个时间步上的St图谱，如图14，可见St数谱特征与升力时程类似，峰值St数也为0.277。

图12　升力系数随来流攻角的变化Fig.12 Lift coefficient against wind angles of attack

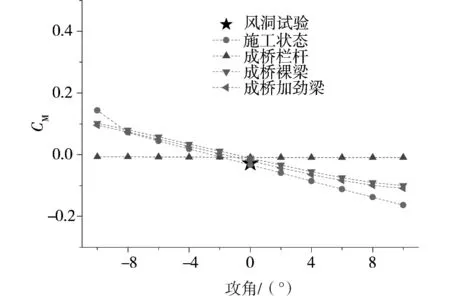
图13　扭矩系数随来流攻角的变化Fig.13 Moment coefficient against wind angle of attack

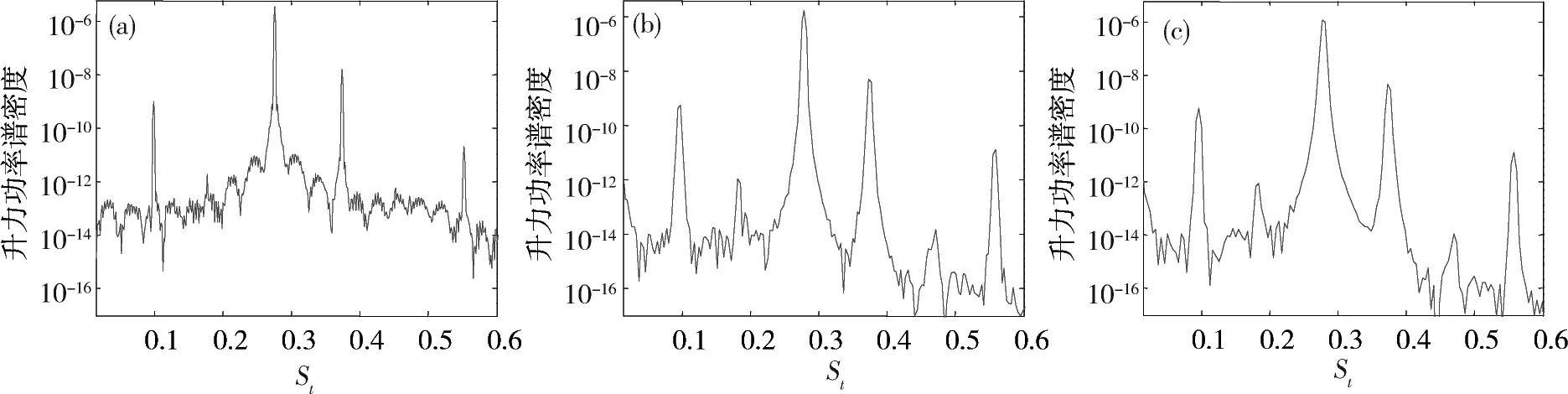
(a)ΔtU0/B =3.1×10-3；(b)ΔtU0/B=1.0×10-3；(c)ΔtU0/B=3.1×10-4图14　升力时程对St数的功率谱Fig.14 Power spectrum of lift records versus St number

(a)ΔtU0/B =3.1×10-3；(b)ΔtU0/B=1.0×10-3；(c)ΔtU0/B=3.1×10-4图15　尾迹竖向速度St数谱Fig.15 Power spectrum of wake vertical velocity versus St number

4.2成桥阶段

图16为ΔtU0/B=1.5×10-3，分别基于栏杆、裸梁和加劲梁整体升力时程获得的St数谱。可见所有时程均包含多个频率成分，即为多阶涡脱；栏杆的第1阶脱落频率高，且也为裸梁的峰值涡脱频率，这可能是栏杆对梁体的气动干扰作用产生。裸梁St谱上可见一个低频的涡脱，值为0.12。成桥加劲梁St图谱显示该低频成分与峰值成分的相对能量较大，而对应栏杆第1阶涡脱的能量反而变小，这可能是栏杆和裸梁的升力在这个频率点反相叠加所致。

图6示气动力系数计算不需很小的时间步，但本文研究了时间步进一步减小后St数谱的变化特征。此时涡脱仍表现为多阶特征，且大部分涡脱频率对应的St数非常高，如图17所示。这些高阶St数是施工阶段没有的，根据栏杆尺度和涡脱频率推断是由栏杆部分漩涡脱落导致。需要指出，漩涡St数大小和排序只有当时间步小到一定值后才保存不变。表2为成桥阶段涡脱St数前5阶排序。当无量纲时间步大小为6.2×10-4，对应在栏杆涡脱1个周期此内有不少于100个时间步时，成桥加劲梁的低阶涡脱St数为0.12，与风洞试验完全吻合[10]。此后时间步再减小，不仅成桥涡脱的前5阶频率的排序不变，而且对应加劲梁的涡脱频率保持为第1峰值频率，如图18～19所示。

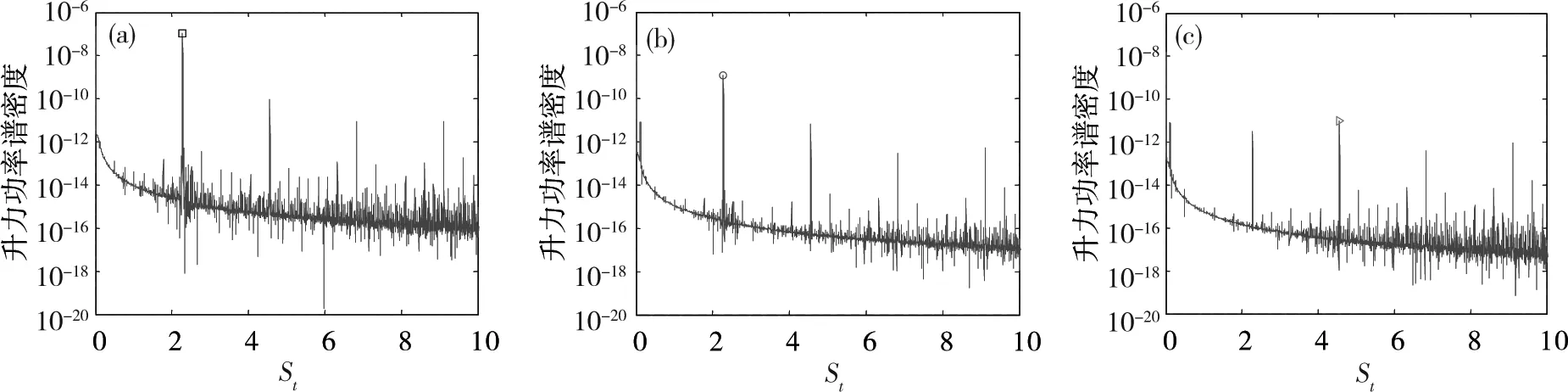
(a)栏杆；(b)裸梁；(c)加劲梁整体图16　ΔtU0/B=1.5×10-3升力时程St数谱Fig.16 St number at ΔtU0/B =1.5×10-3

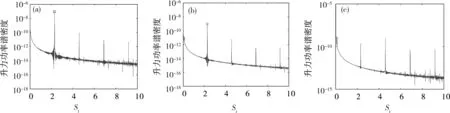
(a)栏杆；(b)裸梁；(c)加劲梁整体图17　ΔtU0/B=6.2×10-4升力时程St数谱Fig.17 St number at ΔtU0/B =6.2×10-4

在主梁后缘点往下游平移1B的尾迹中监测流动的竖向速度Vy时程，并基于PSD分析获得的对应3个时间步上的St图谱见图20。可见栏杆虽然贡献了多个高阶涡脱频率，但加劲梁的涡脱已稳定地维持为峰值频率，对应的加劲梁St数为0.12。图21是绕施工和成桥阶段加劲梁的涡量图。可见成桥阶段在两侧和中央栏杆上均产生了强烈的漩涡脱落，特别是迎风侧栏杆，导致桥面以上和尾迹涡量显著增强。另外，栏杆的引入也使得底板以下流动的涡量增大，箱梁后部尾迹变宽。

表1　涡脱St数谱随无量纲时间步的变化Table 1 Vortex shedding Stspectrum against time step size

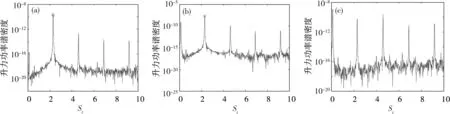
(a)栏杆；(b)裸梁；(c)加劲梁整体图18　ΔtU0/B=1.55×10-4升力时程St数谱Fig.18 St number at ΔtU0/B =1.55×10-4

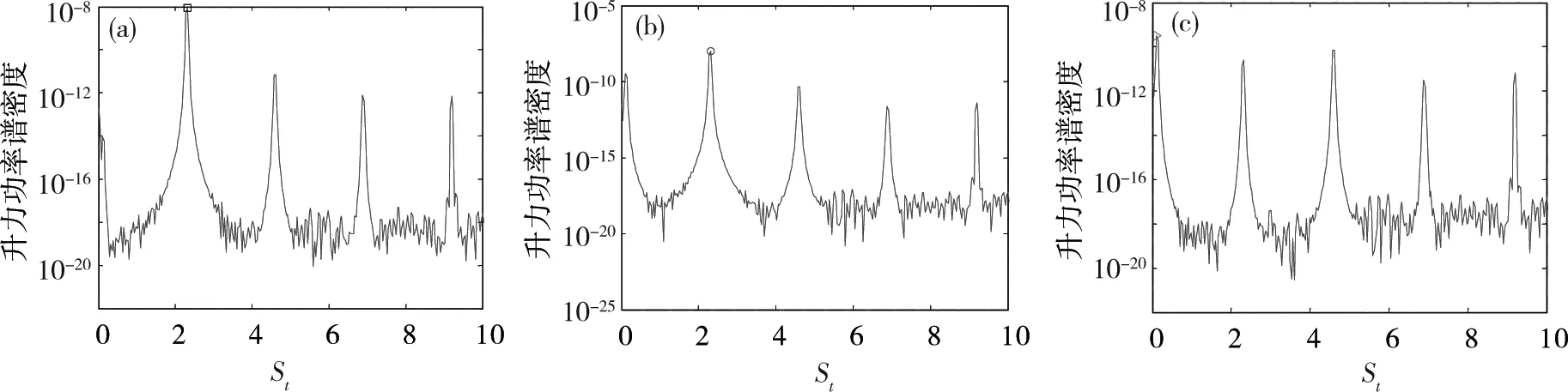
(a)栏杆；(b)裸梁；(c)加劲梁整体图19　ΔtU0/B=3.1×10-5升力时程St数谱Fig.19 St number at ΔtU0/B =3.1×10-5

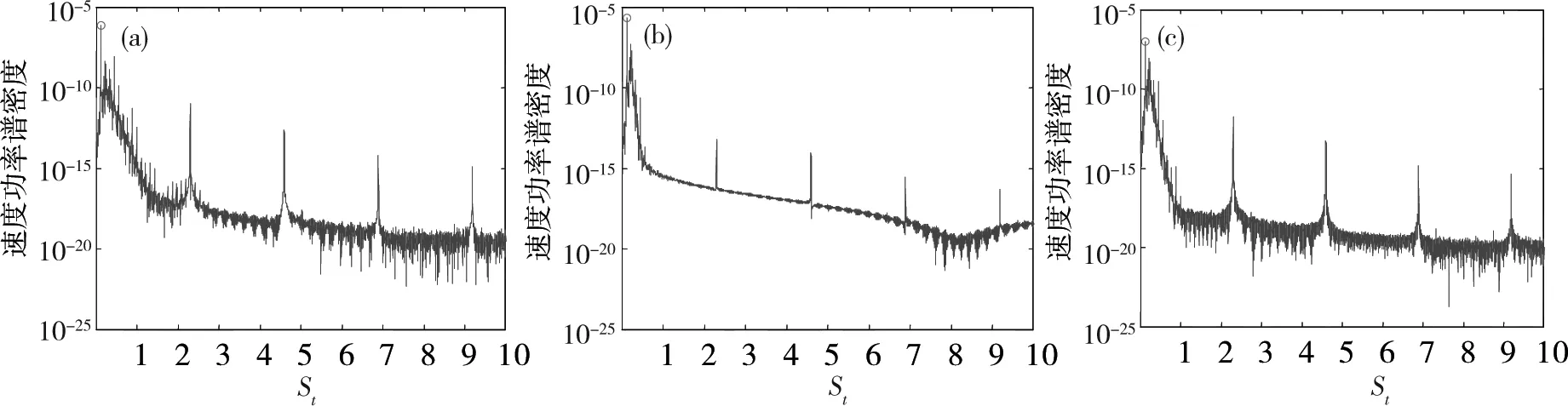
(a)ΔtU0/B=6.2×10-4；(b)ΔtU0/B=1.55×10-4；(c)ΔtU0/B=3.1×10-5图20　尾迹竖向速度St数谱Fig.20 St numbers based on wake vertical velocity

(a)施工阶段；(b)成桥阶段图21　绕加劲梁的涡量云图Fig.21 Vorticity plot around bridge girder

5　主梁表面平均压力系数分布

为考察桥面栏杆布设前后主梁表面平均压力分布的变化，在施工和成桥加劲梁表面分别布设了160个瞬态压力监测点，这些监测点布设根据物面压力场变化的规律，在压力梯度大的位置，如棱角处加密，便于捕捉压力的快速变化。

定义测点的压力系数为,

Cp=(P-P0)/(0.5ρU02)

(10)其中：P为监测点静压；P0为设置在入口边界的参考压。通过大量时间步计算可统计获得监测点压力系数平均值，如图22所示。图中曲线与断面轮廓线间画填充线的为负压系数，无填充线的为正压系数。

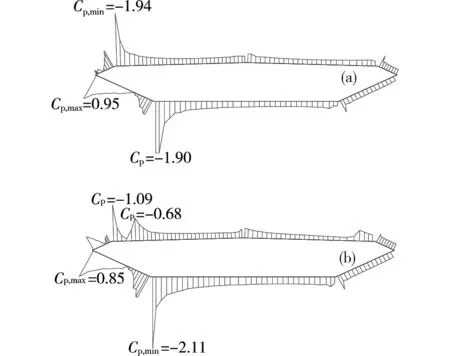
(a) 施工阶段；(b) 成桥阶段图22　主梁时均压力系数分布Fig.22 Time averaged pressure coefficients on girder surface

与施工阶段相比，成桥栏杆下方箱梁表面出现了局部负压峰值。在箱梁表面的大部分区域，特别是主梁中心线下游，施工和成桥的压力分布差别很小。栏杆的引入使得梁体峰值正压系数减小，前缘点上部的正压区增大。施工阶段位于顶板前缘的峰值负压点，由于成桥栏杆对流动的阻挡作用，在成桥阶段中负压绝对值显著减小，成桥阶段的峰值负压位于底板前缘点，且负压绝对值更大。由于棱角负风压尖峰分布往往隐含棱角处强烈的流动分离，因而可以认为，栏杆的引入使得靠近栏杆的箱梁顶板前缘点的分离减弱，而使得远离栏杆的底板前缘点的分离增强，实际钝化了箱梁气动外形，这也可从图23的瞬态压力云图看出。

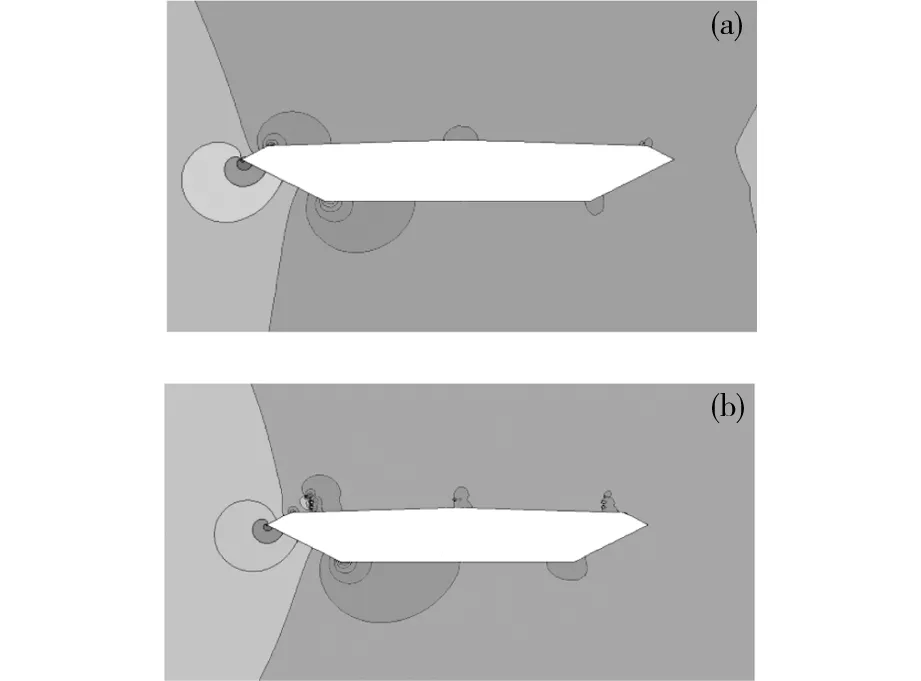
(a) 施工阶段；(b) 成桥阶段图23　绕加劲梁的瞬态压力云图Fig.23 Instantaneous pressure contours around stiffening girder

6　结论

1)0°攻角下与风洞试验基本吻合的成桥阶段气动力系数和涡脱St数，说明基于SSTk-ω湍流模型的二维RANS方法能较准确地预测包含栏杆的成桥加劲梁气动特性。

2)与施工阶段相比，桥面栏杆虽然局部改变了梁体迎风侧风压分布，但对梁体绝大部分区域的风压分布影响小；桥面栏杆显著钝化了扁平箱型加劲梁的气动外形，其对成桥加劲梁阻力的贡献率在0o攻角时达到38%，是其对加劲梁挡风面积贡献的4倍，在-10o～+10o范围内其阻力贡献率最小也达到22%。

3)施工和成桥阶段加劲梁均呈现多阶涡脱特征，但其峰值St数明显不同。施工阶段峰值占优的高阶涡脱St数显著高于风洞试验结果，且不受时间步细化的影响；但当成桥阶段CFD计算时间步足够小后，可获得与风洞试验一致的低阶涡脱占优的St数。

综上所述，应改变传统CFD模拟忽略桥面附属设施研究成桥气动特性的做法，注重大跨度桥梁栏杆抗风设计，在抗风设计中重视桥面栏杆对桥梁主梁气动力和漩涡脱落特性的影响。

[1] Larsen A, Esdahl S, Andersen J, et al. Storebalt suspension bridge-vortex shedding excitation and mitigation by guide vanes [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2000, 88: 283-296.

[2] Li Hui, LAIMA S, OU Jingping, et al. Investigation of vortex-induced vibration of a suspension bridge with two separated steel box girders based on field measurements[J]. Engineering Structures, 2011,33(6):1894-1907.

[3] 黄智文,陈政清.MTMD在钢箱梁悬索桥高阶涡激振动控制中的应用[J].振动工程学报,2013,26(6)：908-915.

HUANG Zhiwen, CHEN Zhengqing, Application of multiple tuned mass vibration of suspension damper for higher-order vortex-induced bridge with steel box girder[J]. Journal of Vibration Engineering,2013,26(6):908-915.

[4] 陈政清.大跨度钢箱梁悬索桥的高阶模态涡激共振问题研究[C]//第二十届全国桥梁学术会议论文集,北京:人民交通出版社,2012:756-763.

CHEN Zhengqing, Study on high-order modal vortex-induced vibration of steel box girder on long-span suspension bridge[C]// Proc. of the 20thChina National Conference on Bridges, Beijing: China Communications Press, 2012:756-763.

[5] 祝志文,邓燕华,陈魏.圆柱高Re数绕流特性的大涡模拟研究[J]，振动工程学报，2014,27(1):51-59.

ZHU Zhiwen, DENG Yanhua, CHEN Wei. Large eddy simulation of flow around circular cylinder under high reynolds number[J]. Journal of Vibration Engineering，2014,27(1): 51-59.

[6] Larsen A, Walther J H. Aeroelastic analysis of bridge girder sections based on discrete vortex simulations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997,67&68: 253-265.

[7] Ge Y, Xiang H. Recent development of bridge aerodynamics in China[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008,96(6-7): 736-768.

[8] ZHU Z, GU M, CHEN Z. Wind tunnel and CFD study on identification of flutter derivatives of a long-span self-anchored suspension bridge[J]. Computer-aided Civil and Infrastructure Engineering, 2007,22 (7): 541-554.

[9] Menter F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32:269-289.

[10] Reinhold T A, Brinch M, Damsgaard A. Wind tunnel tests for the great belt link[C]// Proc. Aerodynamics of Large Bridges, Balkema, Rotterdam, 1992:255-267.

[11] Larsen A. Aerodynamic aspects of the final design of the 1624m suspension bridge across the great belt[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 48:261-285.

Investigation on effects of deck rails on aerodynamicsand vortex shedding pattern of bridge girders

ZHU Zhiwen1,2

(1.School of Civil Engineering, Hunan University, Changsha 410082, China;2.Key Laboratory for Wind and Bridge Engineering of Hunan Province, Hunan University, Changsha 410082, China)

In order to evaluate the effects of deck rails on aerodynamics of bridge girders, CFD simulations were carried out to investigate flow field around girder of the Great Belt East Bridge main span, in both construction stage and in-service stage. The Reynolds-Averaged Navier-Stokes (RANS) equation and SST k-ω turbulent model were employed，with Reynolds number of 3.18×105. Aerodynamic coefficients of the girder in two stage were obtained under different wind angles of attack. The mean pressure distribution around the girder surface and vortex-shedding Strouhal(St) number are also obtained. The results agrees well with available wind tunnel tests. It is found that the deck rails would bluff the bridge girder, and change pressure distribution on girder windward side. Compared with construction stage under the same wind angle of attack, the involved deck rails will result in significant increase on drag coefficients, with a maximum increase of 38% at zero angle of attack. Both the construction stage and in-service stage indicate a multiple vortex-shedding feature, with high-order vortex shedding dominated regardless of time step refinement in the former. Besides, low-order vortex shedding dominated can be predicted in the later if time step size is small enough. It is found that previous CFD simulations of girder in operation stage without deck rails should be avoided, and aerodynamic design of crash barriers, different vortex-shedding features of girders between the construction stage and operation stage should be put great emphasis.

long-span bridges; aerodynamics; vortex shedding; deck rails; turbulence modeling

2015-12-14

国家重点基础研究发展计划(973计划)项目(2015CB057701，2015CB057702)；国家自然科学基金资助项目(51278191)；湖南省交通科技计划资助项目(201522)

祝志文(1968-)，男，湖南益阳人，教授，博士，从事工程结构抗风和抗震、钢桥设计和数值风洞研究；E-mail:zwzhu@hnu.edu.cn

U448.213

A

1672-7029(2016)10-1945-10