一类广义Lyapunov矩阵方程的正定解

李春梅，段雪峰，彭振赟，江祝灵

（桂林电子科技大学数学与计算科学学院，广西 桂林　541004）

一类广义Lyapunov矩阵方程的正定解

李春梅，段雪峰，彭振赟，江祝灵

（桂林电子科技大学数学与计算科学学院，广西 桂林541004）

研究了双线性系统中的一类广义Lyapunov矩阵方程的正定解.基于混合单调算子不动点定理，给出新的存在正定解的充分条件，构造了求其正定解的不动点迭代方法，并给出了迭代误差估计公式.数值实验表明新方法是可行的.

广义Lyapunov矩阵方程；双线性系统；正定解；充分条件；迭代方法

1　引言

本文研究如下广义Lyapunov矩阵方程：

的正定解，其中A，N1，N2，···，Nm是n×n阶实矩阵，Q是n×n阶对称正定矩阵.令

则双线性系统

的可达格拉姆矩阵P就是广义Lyapunov矩阵方程（1.1）的正定解，其中Q=BBT.因此，广义Lyapunov矩阵方程（1.1）的正定解在双线性系统的可达格拉姆矩阵的计算中起着重要作用，详见文献［1-3］.

自从上个世纪开始，人们对标准的Lyapunov矩阵方程（即矩阵方程（1.1）在m=0时的情形）进行了系统深入的研究，发展了许多有效的数值方法.这些迭代方法主要分为直接法和迭代法两大类，直接法主要利用矩阵分解、分块技术，矩阵广义逆和矩阵直积给出解析解的方法，比如：Bartels-Stewart方法［4］，Hammarling方法［5］等，而迭代方法（如：Krylov子空间方法［6］，ADI方法［7］，矩阵符号函数法［8］和保结构算法［910］）主要是建立某种迭代格式，让迭代格式产生的序列收敛于Lyapunov矩阵方程的解.然而广义Lyapunov矩阵方程（1.1）在m≥1时的可解性理论和数值方法相对比较少，其主要原因是矩阵方程（1.1）的结构比较复杂，难以刻画它的正定解.文［1］给出了矩阵方程（1.1）存在正定解的充分条件，然而这些条件建立在抽象的线性算子理论和谱分析的基础之上.通过矩阵拉直算子和Kronecker积，文［1112］将矩阵方程（1.1）转化成线性方程组，给出了一些有解的充分条件，还设计了一种参数迭代求解方法.

据我们所知，广义Lyapunov矩阵方程（1.1）的正定解的存在性还是一个难题.本文将利用混合单调算子不动点定理，给出一个新的存在正定解的充分条件，构造了求其正定解的不动点迭代方法，并给出了迭代误差估计公式.

2　预备知识

本文用Rn×n表示n×n阶实矩阵构成的集合，SRn×n表示n×n阶对称矩阵组成的集合.B＞0（B≥0）表示矩阵B对称正定（半正定）.B＞C（B≥C）表示矩阵B-C正定（半正定）.如果矩阵X满足B＜X＜C，我们记为X∈（B，C）.λ1（B）和λn（B）分别表示n×n对称矩阵B的最大和最小特征值.表示n×n阶半正定矩阵构成的集合.BT表示矩阵B的转置，Om×n表示m×n阶零矩阵.‖B‖表示矩阵B的谱范数.对于n×n阶正定矩阵Q，Q-范数定义如下

集合SRn×n上定义了Q-范数就形成一个完备的度量空间（详见文献［1］）.

引理 2.1［13］设A和B是n×n阶正定矩阵，则0≤Tr（AB）≤‖A‖Tr（B）.

引理 2.2（混合单调算子不动点定理［14］）设（W，≤）是一个偏序集，d是W上的度量，它使得W构成一个完备的度量空间.设映射F：W×W→W连续且在集合W上混合单调.假如存在δ∈［0，1）对所有的x≥u和y≤v满足

如果

（i）存在x0，y0∈W 使得x0≤F（x0，y0）和y0≥F（y0，x0）成立；

（ii）任何一对元素都有上界和下界，即对任意（x，y）∈W×W 都存在 z1和 z2使得x，y≤z1和x，y≥z2成立；那么存在唯一的使得

另外，由xk+1=F（xk，yk）和yk+1=F（yk，xk）产生的序列｛xk｝和｛yk｝收敛于它的误差估计式为

这里映射F：W×W→W混合单调的意思是映射F（x，y）关于x单调递增，关于y单调递减，即

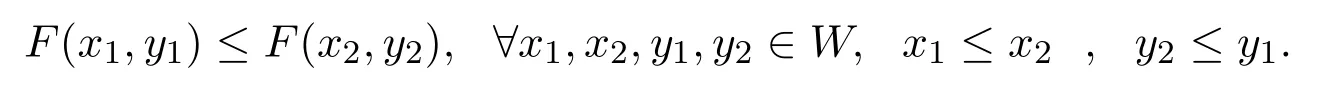
3　主要结论

本节中，我们利用混合单调算子的不动点定理得到矩阵方程（1.1）存在对称正定解的新的充分条件，构造一种迭代方法计算其对称正定解，同时迭代方法的误差估计公式也被给出.

定理 3.1设F=A+In.如果

4　数值实验

本节将利用数值例子验证迭代方法（3.2）的可行性.实验程序都是用MATLAB R2010a编写.对于迭代方法（3.2），我们定义相对误差

所有实验的停机标准为R（Xk）≤1.0×10-10，R（Yk）≤1.0×10-10.

例4.1考虑广义Lyapunov方程：

（1）设n=8，容易验证定理3.1的条件满足，则可利用迭代方法（3.2）计算矩阵方程（4.1）的唯一正定解迭代3 0步后，得到它的相对残差为R（X30）≈8.58×10-11.

（2）设n=100或300，容易验证定理3.1的条件满足，则可利用迭代方法（3.2）计算矩阵方程（4.1）的唯一正定解相对残差R（Xk）和R（Yk）的收敛曲线见图1.

图1　相对残差R（Xk）和R（Yk）的收敛曲线

例4.1说明如果A，Nj和Q满足定理3.1的条件，则由迭代方法（3.2）产生的矩阵序列｛Xk｝和｛Yk｝都收敛于矩阵方程（1.1）的唯一正定解

5　结论

本文研究了双线性系统模型降阶中的一类广义Lyapunov方程.利用混合单调算子的不动点定理得到了该方程存在唯一正定解的充分条件，构造了迭代求解方法，并给出了迭代方法的误差估计公式.文章最后利用数值例子验证了迭代方法的可行性.

［1］Benner P，Damm T.Lyapunov equations，energy functions，and Model order reduction of bilinear and stochastic systems［J］.SIAM J.Control Opt.，2011，40：686-711.

［2］Ferrante A，Ntogramatzidis L.The generalised discrete algebraic Riccati equation in linear-quadratic optimal control［J］.Automatica，2013，49：471-478.

［3］Zhang L，Lam J.On H2model reduction of bilinear systems［J］.Automatica，2002，38：205-216.

［4］Bartels R，Stewart G.Solution of the matrix equation AX+XB=C：Algorithm 432［J］.Com.ACM，1972，15：820-826.

［5］Liu Xiping，Jia Mei.Multiple solutions for fractional differential equations with nonlinear boundary conditions［J］.Computers Mathematics with Applications，2010，59（8）：2880-2886.

［6］Jaimoukha I M，Kasenally E M.Krylov subspace methods for solving large Lyapunov equations［J］.SIAM J Numer Anal，1994，31：227-251.

［7］Lu A，Waachspress E L.Solution of Lyapunov equations by alternating direction implicit iteration［J］.Comput.Math.Appl.，2011，21：3-58.

［8］Beavers A N，Demman J E D.A new solution method for the Lyapunov matrix equation［J］.SIAM J Matrix Anal Appl，1975，29：416-421.

［9］黄敬频，于艳.四元素矩阵方程的复转化及保结构算法［J］.纯粹数学与应用数学，2008，24：321-326.

［10］黄敬频.四元素矩阵方程AX+Y B=C的两种最佳逼近解［J］.纯粹数学与应用数学，2004，20：109-114.

［11］黄敬频.求解混合型Lyapunov矩阵方程的参数迭代法［J］.计算数学，2007，29：285-292.

［12］黄敬频.一类混合型Lyapunov矩阵方程的对称正定解［J］.工程数学学报，2008，25：313-320.

［13］Ran A C M，Reurings M C B.A fixed point theorem in partially ordered sets and some applications to matrix equations［J］.Proceedings of AMS，2004，132：1435-1443.

［14］Bhaskar T G，Lakshmikantham V.Fixed point theory in partially ordered metric spaces and applications［J］.Nonlinear Analysis，2006，65：1379-1393.

［15］Agarwal R P，Meehan M，Regan D.Fixed Point Theory and Applications［M］.Cambridge：Cambridge University Press，2011，45-113.

2010 MSC:15A24，65F30，93A15

Positive definite solution of a class of generalized Lyapunov equation

Li Chunmei，Duan Xuefeng，Peng Zhenyun，Jiang Zhuling
（School of Mathematics and Computational Science，Guilin University of Electronic Technology，Guilin 541004，China）

In this paper，we consider the positive definite solution of a class of generalized Lyapunov matrix equation，which arises in the bilinear systems.Based on the fixed point theorem for mixed monotone operator，a new sufficient condition for the existence of a unique positive definite solution is derived.A fixed point iterative method is proposed to compute the unique positive definite solution，and its error estimation is also given.Finally，a numerical example is presented to illustrate the feasibility of the proposed method.

generalized Lyapunov equation，bilinear system，positive definite solution，sufficient condition，iterative method

O178

A

1008-5513（2016）05-0505-10

10.3969/j.issn.1008-5513.2016.05.007

2016-06-30.

国家自然科学基金（11561015；11301107；11261014）；广西自然科学基金（2016GXNSFFA380009；2016GXNSFAA380074）.

李春梅（1984-），硕士，讲师，研究方向：数值代数.