Kolmogorov-Spieqel-Sivashinsky方程的渐近吸引子及维数估计

周萍，邢超，罗宏

（四川师范大学数学与软件科学学院，四川 成都　610066）

Kolmogorov-Spieqel-Sivashinsky方程的渐近吸引子及维数估计

周萍，邢超，罗宏

（四川师范大学数学与软件科学学院，四川 成都610066）

研究了周期边界条件下Kolmogorov-Spieqel-Sivashinsky方程的渐近吸引子，并给出了它的维数估计.首先利用正交分解法构造了一个有限维解序列，然后分两步证明该解序列收敛于方程的真实解.

Kolmogorov-Spieqel-Sivashinsky方程；渐近吸引子；维数估计

1　引言

Kolmogorov-Spieqel-Sivashinsky（KSS）方程：

是Spieqel，Sivashinsky等人在研究Kolmogorov流和可压缩对流的大规模结构时所导出的方程［13］.若方程（1）对x求导数，并令u=ψx，则有

人们在研究无穷维动力系统的过程中，常常对吸引子结构进行探讨，因此相继出现了整体吸引子、近似惯性流形和指数吸引子等概念，2000年，王冠香和刘曾荣也在文献［5］中提出了渐近吸引子这一概念.

定义1.1对一个发展系统记其相空间为H，解算子半群为｛s（t），t≥0｝，吸收集为假设对任意存在N维子空间中的近似解序列满足：

则定义

为系统（3）的渐近吸引子.其中‖·‖H为相空间H的范数，uk（t）依赖于初值u0，而只依赖于吸收集半径，即t∗对中的u0是一致的.

自此概念被提出以后，有关渐近吸引子的成果陆续出现，如2004年，文献［6］得到了相空间上Extended Fisher-Kolmogorov系统的渐近吸引子；2007年，文献［7-8］分别得到了推广的B-BBM方程的渐近吸引子和二维Navier-Stokes方程的渐近吸引子；2014年，张晓明等人在文献［9-10］中分别讨论了Kdv-Burgers-Kuramoto系统和非线性梁方程的渐近吸引子.

本文考虑周期边界条件下导数形式的KSS方程

2　渐近吸引子

首先引入文献［4］关于吸收集的结论，并构造一个有限维解序列.

即

是系统（4）-系统（7）的吸收集.

其中

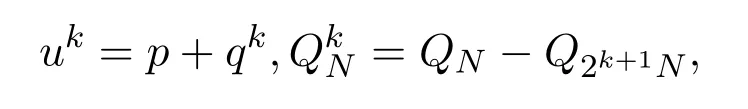
系统（10）-（11）的解的存在唯一性问题类似于原系统.下面将证明渐近解序列uk（x，t）对真解u（x，t）的逼近性.首先证明，对上述所得渐近解序列不会远离吸收集

成立.

［1］Depassier M C，Spiegel E A.The large-scale structure of compressible convection［J］.The Astronomical Journal，1981，86（3）：496-512.

［2］Depassier M C.A note on the free boundary conditions in Rayleigh-Bernard convection between insulating boundaries［J］.Phys.Lett，1984，102A（8）：359-361.

［3］Poyet J P.The Rayleigh-Benard two-dimensional convection in a fluid between two plates of finite conductivity［D］.New York：Columbia University，1983.

［4］Guo B L，Wang B X.Long-time behaviour of the solution for the multidimensional Kolmogorov-Spieqel-Sivashinsky equation［J］.Acta Mathematica Sinica（English Series），2002，18（3）：579-596.

［5］王冠香，刘曾荣.Kuramoto-Sivashinsky方程的渐近吸引子［J］.应用数学学报，2000，23（3）：329-336.

［6］罗宏，蒲志林.Extended Fisher-Kolmogorov系统的渐近吸引子［J］.纯粹数学与应用数学，2004，20（2）：150-156.

［7］何素芳，朱朝生.推广的B-BBM方程的渐近吸引子［J］.四川师范大学学报：自然科学版，2007，30（1）：49-52.

［8］Zhao L N，Zhang X Y，Xing T L.The asymptotic attractor of 2D Navier-Stokes equation［J］.数学研究，2007，40（3）：251-257.

［9］张晓明，姜金平，董超雨.Kdv-Burgers-Kuramoto系统的渐近吸引子［J］.纯粹数学与应用数学，2014，30（6）：595-603.

［10］张晓明，姜金平，董超雨.非线性梁方程的渐近吸引子［J］.数学的实践与认识，2015，45（2）：302-308.

2010 MSC:35B41

The asymptotic attractor and dimensional estimate of Kolmogorov-Spieqel-Sivashinsky equation

Zhou Ping，Xing Chao，Luo Hong
（College of Mathematics and Software Science，Sichuan Normal University，Chengdu610066，China）

In this paper，we study the asymptotic attractor of Kolmogorov-Spieqel-Sivashinsky equation with periodic boundary conditions，and obtain the dimensional estimate of the asymptotic attractor.Firstly，the solution sequence is constructed by using orthogonal decomposition.Secondly，it is proved that the solution sequence converges to solution of the equation by two processes.

Kolmogorov-Spieqel-Sivashinsky equation，asymptotic attractor，dimensional estimate

0175.29

A

1008-5513（2016）05-0457-13

10.3969/j.issn.1008-5513.2016.05.003

2016-07-06.

国家自然科学基金（11271271）；四川省科技计划项目（2015JY0125）.

周萍（1990-），硕士，研究方向：偏微分方程与动力系统.