具有非局部源的退化奇异抛物方程组解的爆破

王胜青，何万生，彭聪明，3

（1.陇南师范高等专科学校数信学院，甘肃 陇南　742500；2.天水师范学院数学与统计学院，甘肃 天水　741000；3.兰州大学数学与统计学院，甘肃 兰州　730000）

具有非局部源的退化奇异抛物方程组解的爆破

王胜青1，何万生2，彭聪明2，3

（1.陇南师范高等专科学校数信学院，甘肃 陇南742500；2.天水师范学院数学与统计学院，甘肃 天水741000；3.兰州大学数学与统计学院，甘肃 兰州730000）

研究了一类新的包含幂函数和指数函数相耦合的具有非局部源的抛物方程组.用正则化的方法证明了局部解的存在唯一性，用上下解方法得到了整体存在和在有限时刻爆破的充分条件.

退化；整体存在性；爆破

1　引言

本文考虑了下述带非局部源的退化奇异反应扩散方程组：

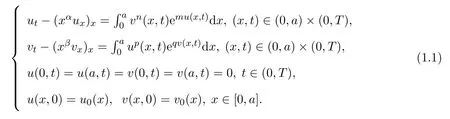
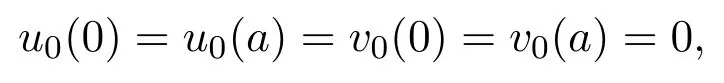
u0及v0满足相容性条件，T＞0，a＞0，α，β∈［0，2）.

设D=（0，a），Ωt=D×（0，t］，及分别是它们的闭包.当x趋于0时ux，uxx和vx，vxx的系数可能趋于0或∞，故方程是退化奇异的.

该问题是一个描述热传导过程的数学模型，具体可参考文献［1］.当α=β=0时，（1.1）是一个具有非局部源的半线性热方程.具有局部源f（u）的热方程已经受到很多关注.最主要的工作是由Friedman和文献［2-4］的作者所做.对非局部源的首个Fujita-型结果是由Galaktionov和Levine在文献［5］中得到的.文献［2-3］得到解爆破的一般条件，证明了爆破集是区域的一个紧子集，而且得到了爆破解的渐进行为.最近，带非局部源热方程的研究引起了很多关注.关于（1.1），当α=β=0时，文献［6-9］都进行了研究.在文献［10］中，作者研究了下述问题：

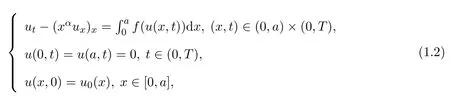
得到了解的局部存在唯一性.在适当条件下，还研究了正解的整体存在性和解在有限时刻的爆破.他们还得到了解的爆破集是整个区域.本文推广了文献［7，10］的结果.但由于退化性的出现，我们用了和文献［7］不同的方法.在第二部分中，建立了比较原理及解的存在唯一性.关于解在有限时刻的爆破将在第三部分中讨论.

2　局部存在性

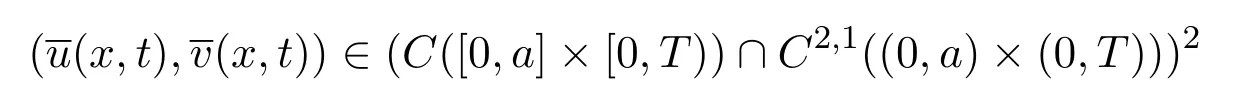
而且满足

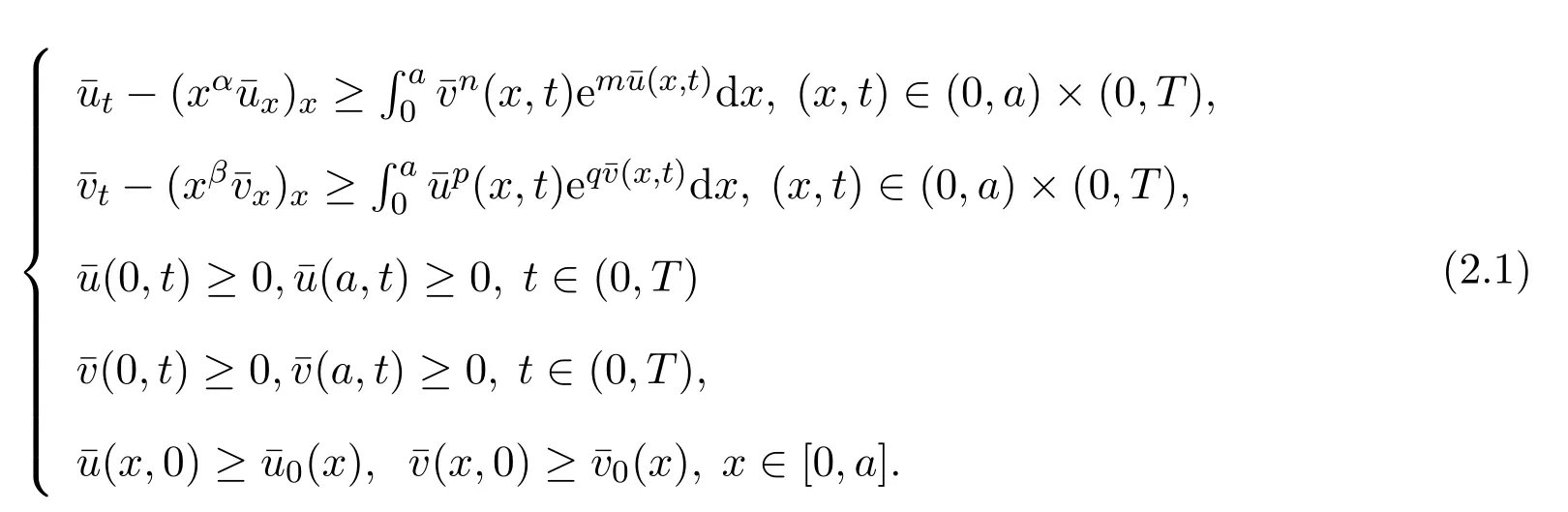
类似地，

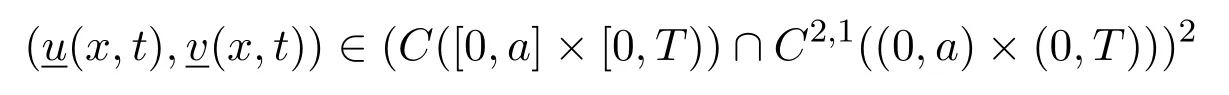
称为下解，如果（2.1）中的所有反向不等号成立.

为了证明问题（1.1）的正解的存在唯一性，必须构建下述比较原理：

引理2.1设r∈（0，T），ci（x，t），di（x，t）（i=1，2）为定义在［0，a］×［0，r］上的连续非负函数，令满足：

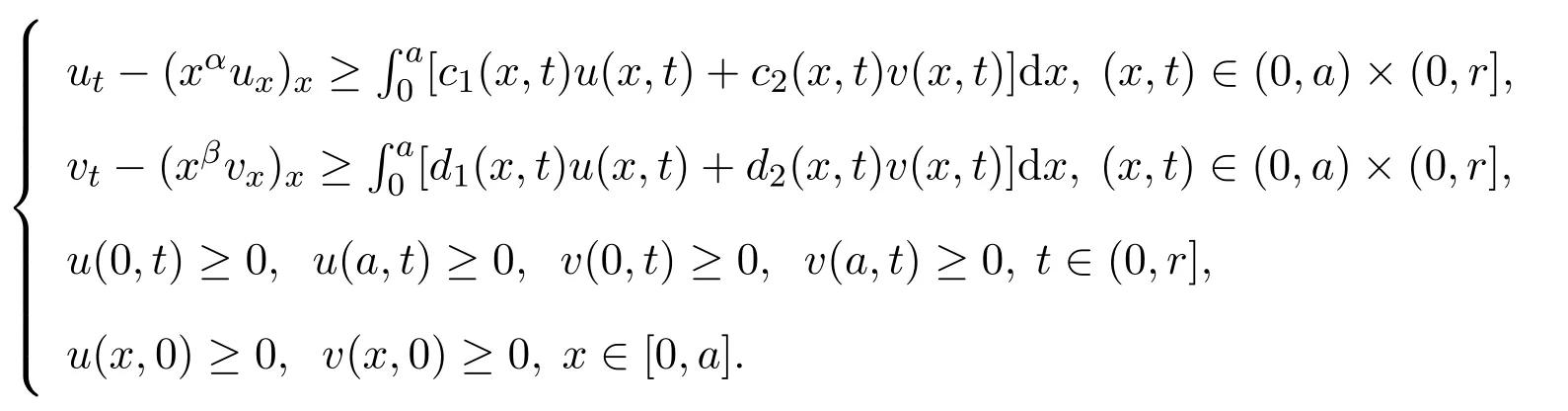
则在［0，a］×［0，T）上，u（x，t）≥0，v（x，t）≥0.

证明 证明类似于文献［11］，引理2.1.

引理2.2设（u（x，t），v（x，t））是问题（1.1）的非负解.假设一对函数

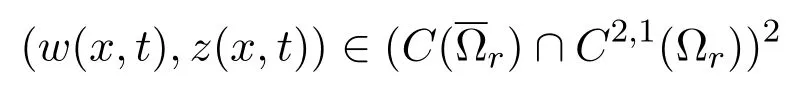
满足

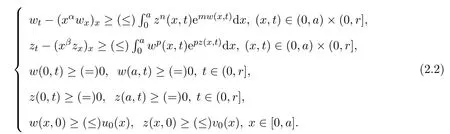
则在［0，a］×［0，T）上，（w（x，t），z（x，t））≥（≤）（u（x，t），v（x，t））.

显然，（0，0）是问题（1.1）的下解，我们还需要构造一个上解.

引理2.3设存在正常数t0（t0＜T）使得问题（1.1）有上解（f（t），g（t））∈（C［0，t0］）2.

为了得到解的存在唯一性，需要一个正则化过程，但该过程是标准的，所以我们直接给出解的存在唯一性定理：

定理2.1存在t0（＜T）使得问题（1.1）有唯一的非负解

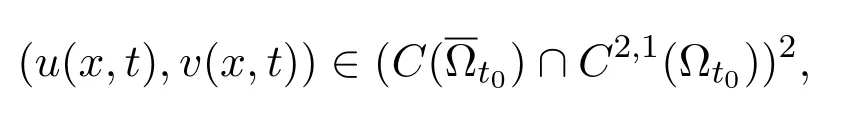
其中α，β∈［0，2）.

证明 证明类似于文献［12］，定理2.5.

定理2.2设T是使得问题（1.1）存在唯一解（u（x，t）的t0的上确界.则问题（1.1）有唯一的非负解

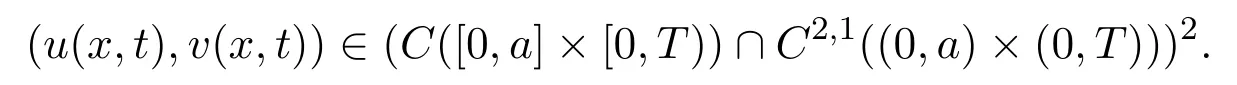
若T＜+∞，则

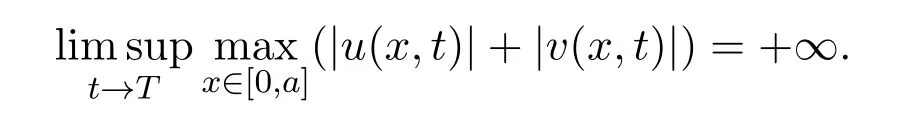
证明 证明类似于文献［13］的定理2.5.

3　整体存在性及爆破

下面考虑问题（1.1）解的整体存在性及在有限时刻的爆破.主要结论如下：

定理3.1 a）若np＞1则问题（1.1）在任意区域（0，a）上对小初值（u0，v0）存在整体解.

b）若np≤1且a适当小，则问题（1.1）对小初值（u0，v0）存在整体解.

定理3.2假定下列条件之一成立：

（i）m＞0；（ii）q＞0；（iii）m=q=0且np＞1.

则对充分大的初值（u0，v0），问题（1.1）的解在有限时刻爆破.

［1］Chan C Y，Chen C S.A numerical method for semilinear singular parabolic quenching problem［J］.Quart.Appl.Math.，1989，47：45-57.

［2］Friedman A，McLeod B.Blow-up of positive solutions of semilinear heat equations［J］.Indiana Univ.Math.J.，1985，34：425-447.

［3］Giga Y，Kohn R V.Asymptotic self-similar blow-up of semilinear heat equations［J］.Comm.Pure.Appl.Math.，1985，38：297-319.

［4］Samarskii A A，Galationov V A，Kurdynumov A P.Blow-up in Quasilinear Parabolic Equations［M］.Berlin：Walter de Gruyter，1995.

［5］Galationov，Victor A，Levine，Howard A.A general approach to critical Fujita exponents in nonlinear parabolic problems［J］.Nonlinear Anal，1998，34（7）：1005-1027.

［6］Wang M X，Wang Y M.Properties of positive solutions for non-local reaction-diffusion problems［J］.Mathematical Methods in the Applied Sciences，1996，14：1141-1156.

［7］Jiang L J，Li H L.Uniform blow-up profiles and boundary layer for a parabolic system with nonlocal source［J］.Mathematical and Computer Modelling，2007，45：814-824.

［8］Bebernes J，Bressan A，Lacey A.Total blow-up versus single point blow up［J］.J.Differential Equations，1988，73：30-44.

［9］Souplet P.Blow-up in nonlocal reaction-diffusion equations［J］.SIAM Journal on Mathematical Analysis，1998，29（6）：1301-1334.

［10］Chen Y P，Liu Q L，Xie C H.The blow-up properties for a degenerate semilinear parabolic equation with nonlocal source［J］.Appl.Math.J.Chinese Univ.Ser.B，2002，17（4）：413-424.

［11］Peng C M，Yang Z D，and Xie B L.Global existence and blow-up for the degenerate and singular nonlinear parabolic system with a nonlocal source［J］.Nonlinear Analysis，TMA，2010，72：2474-2487.

［12］Zhou J，Mu C L，Li Z P.Blow up for degenerate and singular parabolic system with nonlocal source［J］.Boundary Value Problem，2006，21830.

［13］Floater M S.Blow-up at the boundary for degenerate semilinear parabolic equations［J］.Archive for Rational Mechanics and Analysis，1991，114（1）：57-77.

［14］Chen Y P，Liu Q L，Xie C H.Blow-up for degenerate parabolic equations with nonlocal source［J］.Proceedings of the American Mathematical Society，2004，132（1）：135-145.

［15］Mclachlan N W.Bessel Functions for Engineers［M］.London：Clarendon Press，1955.

2010 MSC:35B15

Blow-up profiles for a degenerate and singular nonlinear parabolic system with nonlocal source

Wang Shengqing1，He Wansheng2，Peng Congming2，3
（1.School of Mathematics and Information Science，Longnan Teachers College，Longnan742500，China；2.School of Mathematics and Statistics，Tianshui Normal University，Tianshui741000，China；3.School of Mathematics and Statistics，Lanzhou University，Lanzhou730000，China）

A new degenerate and singular parabolic system with power functions and exponential functions is investigated in this paper.The existence and uniqueness of local solution are proved by using regularization method，moreover the sufficient conditions for the solution that exists globally or blows up in finite time are obtained by method of subsolutions and supersolutions.

degenerate，global existence，blow up

O175.2

A

1008-5513（2016）05-0448-09

10.3969/j.issn.1008-5513.2016.05.002

2016-06-22.

甘肃省“十三五”教育科学规划项目（GS［2016］GHB0185）.

王胜青（1965-），硕士，副教授，研究方向：概率论与数理统计、微分方程.