具有逐项分数阶导数的微分方程边值问题解的存在性

李燕，刘锡平，李晓晨，张莎

（上海理工大学理学院，上海　200093）

具有逐项分数阶导数的微分方程边值问题解的存在性

李燕，刘锡平，李晓晨，张莎

（上海理工大学理学院，上海200093）

研究了一类具有逐项分数阶导数的微分方程边值问题.对参数的各种取值情况进行了全面的分析，运用Banach压缩映射原理和Schauder不动点定理，得到并证明了边值问题解的存在性定理.最后，给出了两个例子来证明结论有效.

分数阶微分方程；逐项分数阶导数；边值问题；Banach压缩映射原理；Schauder不动点定理

1　引言

近年来，由于分数阶微分方程在现代科学各个领域中的广泛应用，其理论研究备受关注［1］.国内外学者已对分数阶微分方程边值问题进行了大量研究（见参考文献［2-11］）.具有逐项分数阶导数的微分方程在振动理论中具有重要的意义，文献［8-11］对于该类微分方程边值问题进行了研究.

文献［9］研究了分数阶非线性微分方程边值问题：

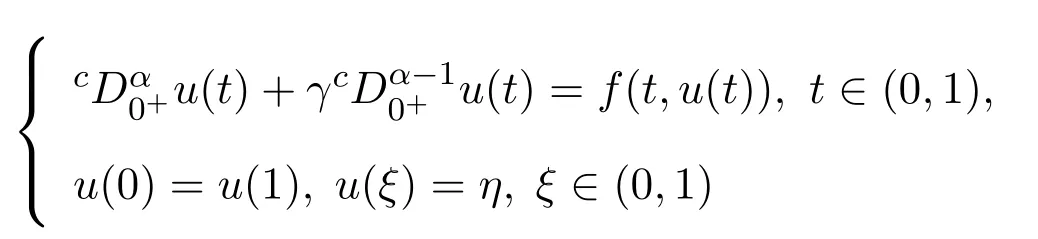
文献［10］研究了如下具有逐项分数阶导数的微分方程三点边值问题：

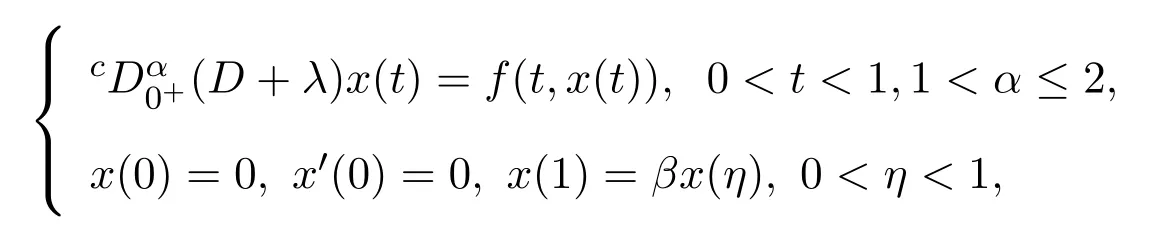
受上述文献的的启发，本文研究如下具有逐项分数阶导数的微分方程边值问题：

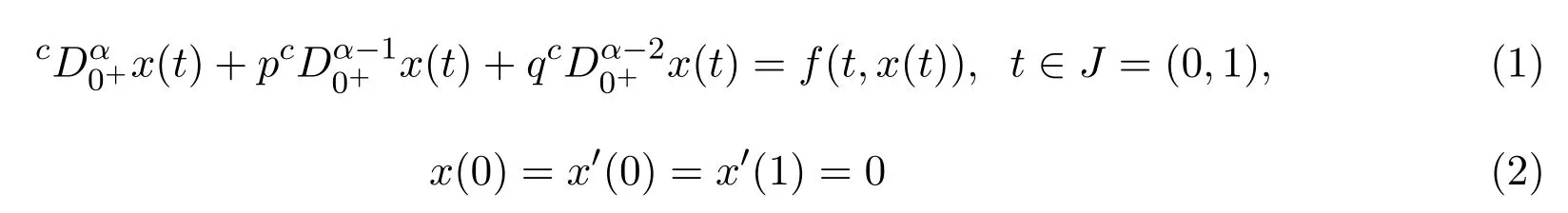
2　预备知识及引理

定义2.1［1］函数y：（0，∞）→R的α＞0阶Riemann-Liouville分数阶积分定义为：

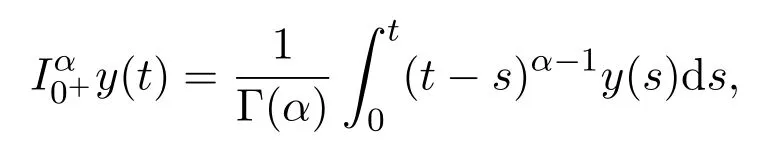
等式右端在（0，∞）有定义.

定义2.2［1］连续函数y：（0，∞）→R的α＞0阶Caputo分数阶导数定义为：

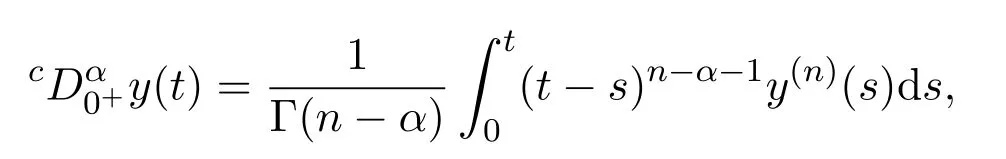
只要等式右端在（0，∞）上有定义.

引理2.1［1］如果y∈Cn（0，1）∩L［0，1］，则

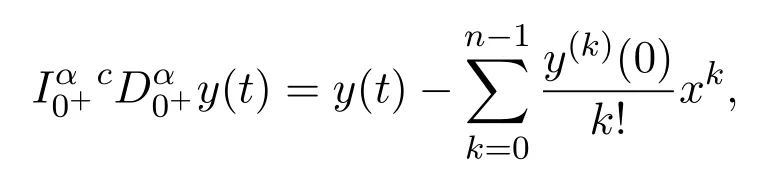
其中n∈N，n-1＜α＜n，n=［α］+1.

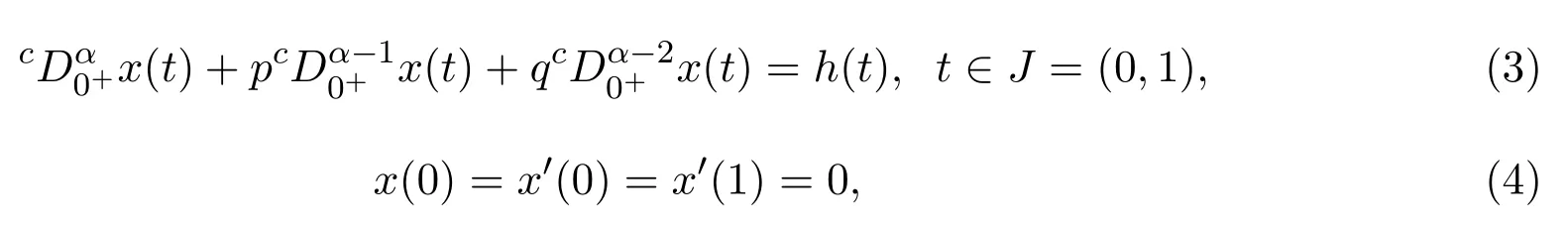
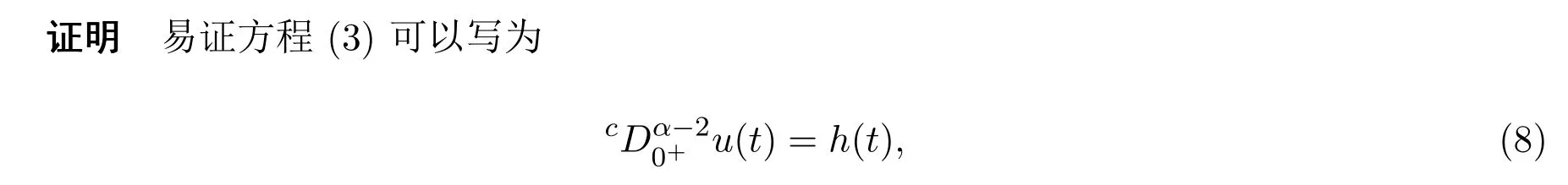
引理2.3（Banach压缩映像原理）设E是Banach空间X中的非空闭子集，映射T是E到自身的映象，如果对任意的x，y∈E，

则存在唯一的x∈E使得Tx=x.

引理2.4（Schauder不动点定理）设E是Banach空间X中的非空闭凸子集，F是E到E的连续映射，使F（E）是X中的相对紧子集，则F在E中至少有一个不动点.

3　边值问题解的存在性

设C［0，1］为区间［0，1］上的连续函数空间，取范数为则C［0，1］为Banach空间.

我们首先估计Green函数 Gi（t，s）的上界.

引理3.1由（5），（6），（7）定义的函数 G1（t，s），G2（t，s），G3（t，s）有以下性质：

1）Gi（t，s）∈C（［0，1］×［0，1］），i=1，2，3；

2）|Gi（t，s）|≤ki（s），i=1，2，3，

其中

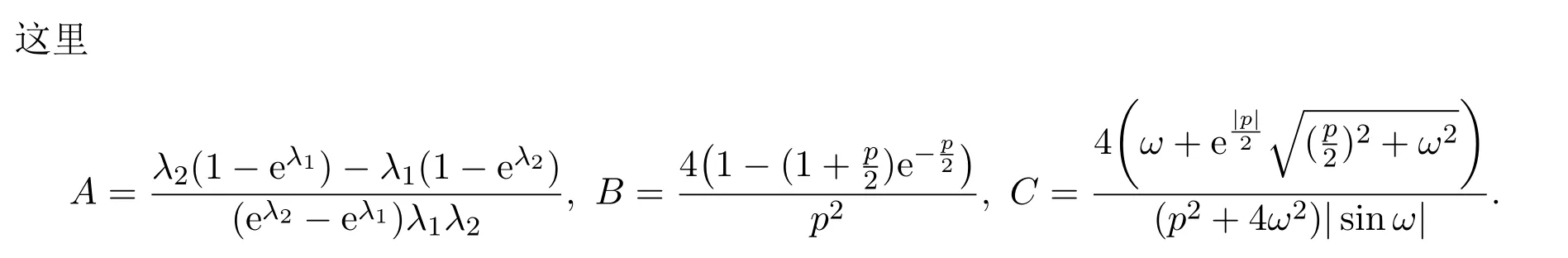
显然，边值问题（1），（2）有解等价于映射 Si存在不动点.

定理3.1假定 f：（0，1）×R→R是连续函数，若存在（0，1）上可积函数 L（t），并且∫使得

则对于参数的p，q的任意取值，当pq≠0时，边值问题（1），（2）都有唯一解.

定理3.2 假定 f：（0，1）×R→R，且存在正常数M，Ni使得

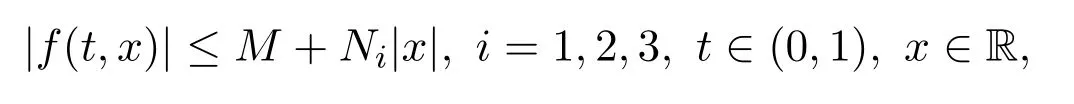
其中Ni满足

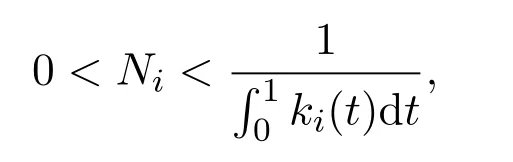
这里ki（t）分别由（10），（11），（12）式定义，那么边值问题（1），（2）式至少有一个解.

4　应用举例

为了证明结论的有效性，给出下面的例子.

例4.1考虑边值问题

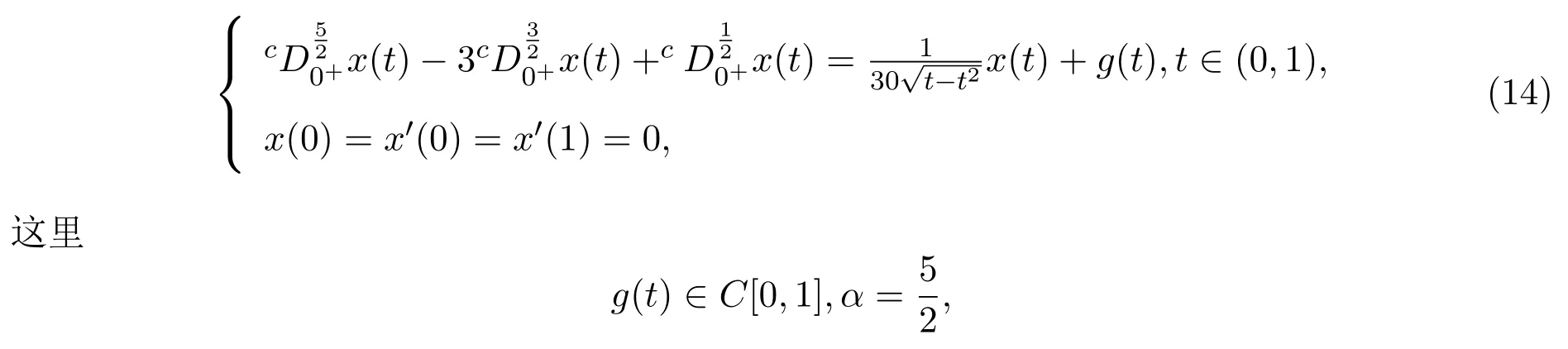
例4.2考虑边值问题

［1］Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations［M］.Amsterdam：Elsevier B.V，2006.

［2］白占兵.分数阶微分方程边值问题理论及应用［M］.北京：陕科学技术出版社，2012.

［3］王晓，刘锡平，邓雪静.一类分数阶奇异微分方程积分边值问题正解的存在性［J］.纯粹数学与应用数学，2015，31（5）：509-517.

［4］张立新，王海菊.含积分边界条件的分数阶微分方程边值问题的正解的存在性［J］.纯粹数学与应用数学，2013，29（05）：450-457.

［5］Liu Xiping，Jia Mei.Multiple solutions for fractional differential equations with nonlinear boundary conditions［J］.Computers Mathematics with Applications，2010，59（8）：2880-2886.

［6］刘帅，贾梅，秦小娜.带积分边值条件的分数阶微分方程解的存在性和唯一性 ［J］.上海理工大学学报，2014，36（5）：409-415.

［7］金京福，刘锡平，窦丽霞.分数阶积分微分方程边值问题正解的存在性［J］.上海理工大学学报，2011，49（5）：824-828.

［8］邓雪静，刘锡平，王晓.具分数微分算子的分数阶微分方程边值问题正解的存在性 ［J］.吉林大学学报，2015，53（05）：857-862.

［9］Chai Guoqing.Existence results for boundary value problems of nonlinear fractional differential equations［J］.Computers and Mathematics with Applications，2011，62（5）：2374-2382.

［10］Bashir Ahmad，Juan J，Nieto.Sequential fractional differential equations with three-point boundary conditions［J］.Computers and Mathematics with Applications，2012，64（10）：3046-3052.

［11］Ahmed Alsaedi，Sotiris K Ntouyas，Ravi P Agarwal，etal.On caputo type sequential fractional dfferential equations with nonlocal integral boundary conditions［J］.Advances in Difference Equations，2015，2015（1）：1-12.

2010 MSC:34A08，34B08，34B15

Existence of solutions for boundary value problem of fractional differential equations involving sequential fractional derivative

Li Yan，Liu Xiping，Li Xiaochen，Zhang Sha
（College of Science，University of Shanghai for Science and Technology，Shanghai200093，China）

This paper investigates the existence of solutions for boundary value problem of fractional differential equations involving sequential fractional derivative.To analyze comprehensively the parameters and by using Banach contraction mapping principle and Schauder fixed point theorem，some new results on the existence of solution for the boundary value problem are obtained.Finally，we give two examples to illustrate our results.

fractional differential equation，sequential fractional derivative，boundary value problem，Banach contraction mapping principle，Schauder fixed point theorem

O175.8

A

1008-5513（2016）05-0470-11

10.3969/j.issn.1008-5513.2016.05.004

2016-05-12.

国家自然科学基金（11171220）；沪江基金（B14005）.

李燕（1991-），硕士生，研究方向：常微分方程理论与应用.

刘锡平（1962-），硕士，教授，研究方向：常微分方程理论与应用.