方程φe(n)=(e=1,2,4)的可解性
2016-11-11王容廖群英
王容,廖群英
(四川师范大学数学与软件科学学院,四川 成都 610066)
方程φe(n)=(e=1,2,4)的可解性
王容,廖群英
(四川师范大学数学与软件科学学院,四川 成都610066)
利用已有的广义欧拉函数的准确计算公式来研究方程φe(n)的可解性,其中n为正整数,d为n的正因子.并利用初等的方法和技巧给出方程的全部正整数解(n,d).
广义欧拉函数;丢番图方程;正整数解
1 引言
定义 1.1[1-2]正整数n的广义欧拉函数定义为:

即φe(n)等于序列中与n互素的数的个数,其中e为正整数.容易证明:
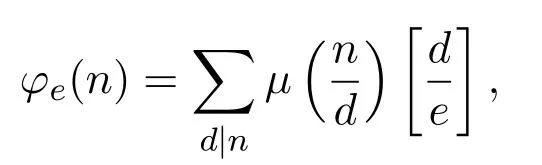
其中[·]是高斯函数,µ(n)是麦比乌斯函数,即

其中且αi≥0,pi(1≤i≤s)为不同的素数.特别的,当e=1时,即

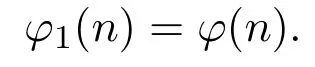
熟知,φ(n)表示序列0,1,2,···,n-1中与n互素的整数个数,即著名的欧拉函数[3].该函数有着很广泛的应用,例如,求离散数学中循环群的生成元,同时它也是RSA公钥密码体制得以建立的重要数学工具之一[4].
事实上,φe(n)的定义是蔡天新等人为将Lehmer同余式从模素数的平方推广到模任意整数的平方时所给出的.易知
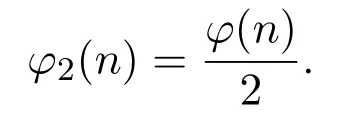
进而,蔡天新等人给出了
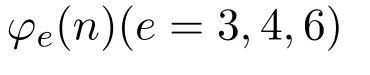
的准确计算公式[5-7].
蔡天新等人不仅完全确定了广义欧拉函数 φe(n)(e=1,2,3,4,6)的计算公式,还研究了φe(n)和φe(n+1)(e=4,6)同为奇数时n的取值;同时,近几年也有很多关于欧拉函数和广义欧拉函数方程的研究.比如,吕志宏[8]用初等的方法研究了方程
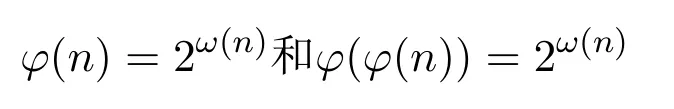
的可解性.孙翠芳,程智[9]研究了方程
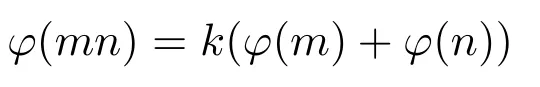
的可解性,同时获得了该方程的所有正整数解,其中k为素数.田呈亮等人[10]给出了方程

的所有正整数解.同样,人们也希望利用广义欧拉函数的准确计算公式来讨论一些不定方程的解.本文相关问题研究,讨论方程

的全部正整数解(n,d),其中n为正整数,d为n的正因子,d≥2且e=1,2,4.为求解方程(1),需要φ4(n)的准确计算公式,即如下
引理1.1[6]设
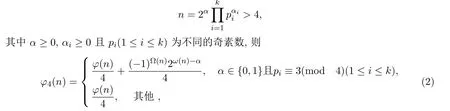
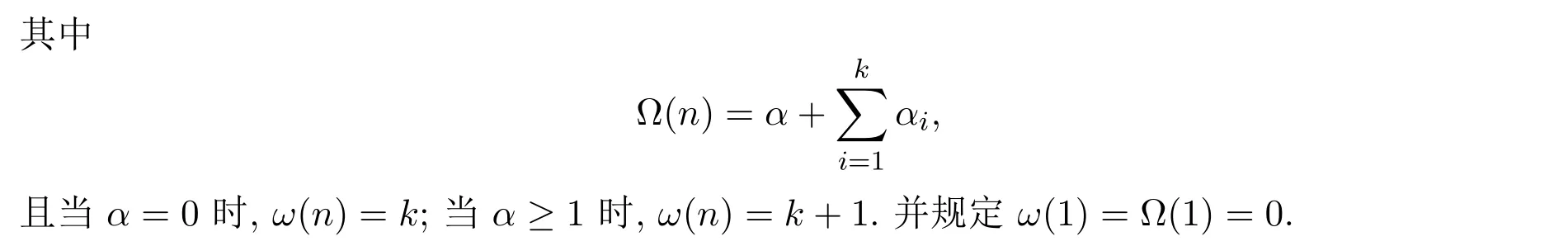
我们证明了如下主要结果.
定理1.1设正整数n=2α,其中α≥3.则方程(1)的全部正整数解为
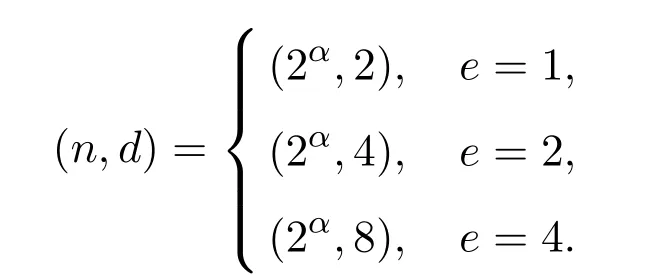

(1)若α=0且存在pi≡1(mod 4).则方程(1)的全部正整数解为

(2)若α=1且存在pi≡1(mod 4).则方程(1)的全部正整数解为

(3)若α≥2,则方程(1)的全部正整数解为
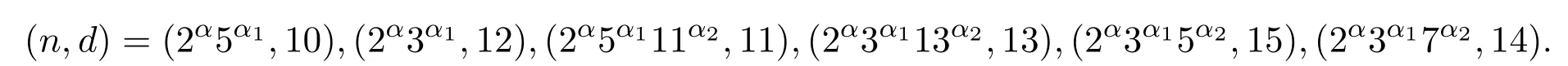
定理1.5设e=4,正整数
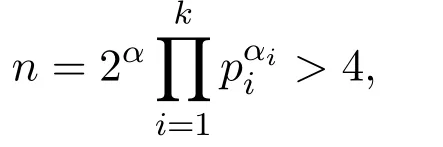
其中α∈{0,1},且∀i=1,···,k,αi≥1,奇素数pi≡3(mod 4),p1<p2<···<pk.则方程(1)的全部正整数解为

2 主要结果的证明










3 小结
为将Lehmer同余式的模从素数的平方推广到任意整数的平方的情形,蔡天新等人定义了广义欧拉函数φe(n),并且给出φe(n)(e=1,2,3,4,6)的准确计算公式,这些公式为讨论广义欧拉函数的性质及应用带来了很多方便.进而,利用这些公式讨论了φe(n)和φe(n+1)同为奇数时n满足的条件[6-7].本文基于φe(n)(e=1,2,3,4,6)的证明,给出了正整数n的广义欧拉函数的几个充分条件,由此得到相应的φ5(n)的奇偶性判别.最后给出了的部分正整数解以及的全部正整数解,其中n是正整数,d是n的正因子.但一般情形下φe(n)的准确计算公式并没有完全确定,有待进一步研究.
[1]Cai T X.A congruence involving the quotients of Euler and its applications(I)[J].Acta Aritmetica,2002,103(4):313-320.
[2]Cai T X,Fu X D,Zhou X.A congruence involving the quotients of Euler and its applications(II)[J].Acta Aritmetica,2007,130(3):203-214.
[3]Kenneth Ireland,Michael Rosen.A classical introduction to Modern Number Theory[M].New York:Springer-Verlag,1990.
[4]李铁牛,李红达.基于欧拉函数秘密分享的RSA私钥的理性分布计算[J].计算机工程与科学,2010,32(9):11-17.
[5]Cai T X,Shen Z Y,Hu M J.On the parity of the generalized euler function[J].数学进展,2013,42(4):505-510.
[6]丁煜.广义欧拉函数及其性质[D].浙江:浙江大学数学系,2008.
[7]Shen Z Y,Cai T X,Hu M J.On the parity of the generalized euler function(II)[J].数学进展,2016.
[8]吕志宏.一个包含Euler函数的方程[J].西北大学学报,2006,36(1):17-20.
[9]Sun C F,Cheng Z.Some kind of equations involving Euler funcion φ(n)[J].数学研究,2010,43(4):364-369.
[10]田呈亮,付静,白维祖.一个包含欧拉函数的方程[J].纯粹数学与应用数学,2010,26(1):96-98.
2010 MSC:11D72,11P55
On the solvability of the equation φe(n)=(e=1,2,4)
Wang Rong,Liao Qunying
(Institute of Mathematics and Software Science,Sichuan Normal University,Sichuan,Chengdu 610066,China)
In order to generalize Lehmer's congruences from modulo prime squares to modulo integer squares,Cai defined the generalized Euler function.The paper studies the solvability of the Diophantine equationwhere n is a positive integer and d is a positive factor of n.By the elementary methods and techniques,the solvability of the Diophantine equationrelated to the generalized the Euler function φe(n)(e=1,2,4)is studied.And then all solutions for the Diophantine equationare given.
generalized Euler function,Diophantine equation,positive integer solution elementary method,conjecture
O156.4
A
1008-5513(2016)05-0481-14
10.3969/j.issn.1008-5513.2016.05.005
2016-05-23.
国家自然科学基金重大项目(11401408);四川省教育厅重点项目(142A0034);四川省科技厅计划项目(2016JY0134).
廖群英(1974-),博士生,教授,研究方向:编码与密码学理论.
