2n阶（n-2）-正则二部图的最小基本圈基

何常香，刘伟龙

（上海理工大学 理学院，上海　200093）

2n阶（n-2）-正则二部图的最小基本圈基

何常香，刘伟龙

（上海理工大学 理学院，上海200093）

设图G为2n阶（n-2）-正则二部图.构造了图G的一个基本圈基并且证明了此圈基就是图G的一个最小基本圈基，同时还确定了任意最小基本圈基对应的生成树的结构.

正则二部图；图的圈基；最小圈基；最小基本圈基

0　引　言

设图G为无向图，C为G中的一个圈，对于G中的任意一条边e，e或在C上或不在C上，故圈C可以通过向量γC∈｛0,1｝|E|表示.图G的圈空间是Z2上由｛γC|C是G中的圈｝形成的向量空间.图G的一个圈基由G的一些圈组成，通过圈基中圈的线性组合可以生成G的圈空间.圈基的长度是基中所有圈的长度之和，长度最小的圈基称为图的最小圈基.在文献［1］中定义了圈基的5种分类，分别是基本圈基、弱基本圈基、幺模圈基、整数圈基和无向圈基.在本文中，我们只考虑图的基本圈基.

尽管一个图的最小圈基可以在多项式时间内计算得到［2］，但是对大部分图，要给出其具体的圈基是困难的，这其中某些特殊图类的最小圈基已经被找到［3-5］.在文献［6］中作者证明了计算最小基本圈基的复杂度为APX-hard；在文献［7］中，作者找到了2n阶（n-1）-正则图K2×Kn（这里K2×Kn表示K2与Kn的直积）的一组最小基本圈基.受此启发，本文研究了2n阶（n-2）-正则二部图的最小基本圈基及其对应的生成树的结构.

若G=（V,E）是2n阶二部图，G是完全二部图Kn,n的子图，称Kn,nE（G）为G的二部补图，记为G∗.设V′是V（G）的一个非空子集，以G［V′］表示G的诱导子图.若G是2n阶（n-2）-正则二部图，则G∗是2-正则二部图，即G∗的每一个连通分支都是偶圈.用T表示G的生成树.设v∈A，用NB（v）表示v在B中所有邻点构成的集合，NB′（v）表示v在B中所有不邻点构成的集合.令C是G中的一个圈，顶点集为V（C）=｛v1,v2,···,vs｝，边集为E（C）=｛［v1,v2］,［v2,v3］,···,［vs-1,vs］,［vs,v1］｝.为方便起见，我们用（v1,v2,···,vs）表示圈C，以dG（u,v）表示图G中点u，v间的距离，以d3（u）表示G中与点u距离为3的点的个数.

定义0.1［1］设B=｛C1,C2,···,Cs｝为图G的一组圈基，如果存在G的一棵生成树T使B=｛CT（e）|e∈E（G）E（T）｝，其中CT（e）表示T∪｛e｝中的唯一圈，则B称为图G的一组基本圈基.

在后文中我们简记图G的基本圈基为FCB，长度最小的基本圈基就是图G的最小基本圈基，简记为MFCB.

引理0.1［8］设连通图G有n个顶点，m条边.令Ψ为图G的圈空间，则Ψ的维数为

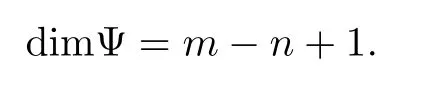
由引理0.1易知，对于2n阶（n-2）-正则二部图G，其圈基的维数为（n-2）n-2n+1= n2-4n+1.

1　主要引理及结论

本节中的图G特指2n阶（n-2）-正则二部图，设其二部顶点集为A，B.根据定义，要构造图的基本圈基，必需先找到该图的一棵生成树.本节中假设n≥5是一个整数.为方便叙述，我们对图G的二部补图G∗的顶点按如下3条规则进行编号，图G∗的二部划分与图G一致.

（a）A部中的点从1开始编号，B部中的点从n+1开始编号.

（b）先对6圈中的点进行编号（若有），其次是大于6的圈（若有），最后是4圈（若有）.

（c）若某圈长度为2（l+1），其中l为正整数，假设它在A部中编号最小的点为k，则将此圈记为（k,n+k+1,k+1,n+k+2,···,n+k+l,k+l,n+k）.

图G的顶点使用G∗的编号.由以上编号规则可知，图G的二部顶点集A=｛1,2,···,n｝，B=｛n+1,n+2,···,2n｝.

下面首先构造图G的一棵生成树.设点n+3在A中的不邻点为s和t，A中点k（不同于点s，t）是点n+1和n+2的一个公共邻点，点m是点s，t的一个公共邻点.由于n≥5，点k，m总是存在的.取图G的部分边组成边集E（T），

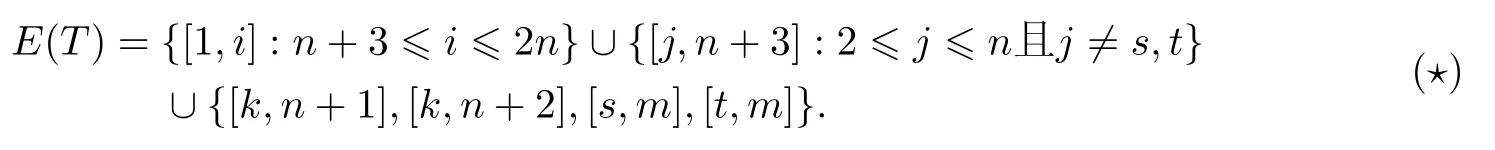
不难看出，这样构造的T连通且|E（T）|=2n-1，所以T是G的一棵生成树.

引理1.1设图G是2n阶（n-2）-正则二部图（n≥5），G∗为G的二部补图.

（1）若G∗含6圈作为子图，则G有一个由2个6圈和n2-4n-1个4圈组成的FCB.

（2）若G∗不含6圈，但含长度大于6的圈作为子图，则G有一个由3个6圈和n2-4n-2个4圈组成的FCB.

（3）若G∗只含4圈作为子图，则G有一个由4个6圈和n2-4n-3个4圈组成的FCB.

证明（1）由于G∗含6圈，按G∗中顶点的编号规则，可将G∗中任一6圈最先编号为（1,n+2,2,n+3,3,n+1），所以在（⋆）式中可取s=2,t=3.将k,m取适当点，这时生成树边集为

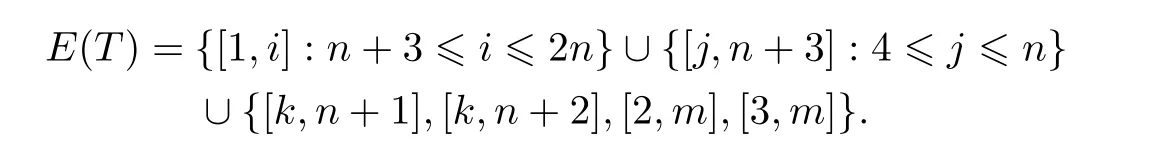
令B是T对应的FCB，边e=［x,y］∈E（G）E（T），其中x∈A,y∈B.下面分4种情况讨论B中圈的长度及数量.

情形1∶x/∈｛2,3｝且y/∈｛n+1,n+2｝.在这种情况下，圈CT（e）=（x,y,1,n+3）.不难看出CT（e）由x和y唯一确定.由定义的树T知，点1为度饱和点，所以x≠1.因此，x有n-3种取法.对于每一个固定的x，y可取｛n+4,n+5,···,2n｝N′B（x）中的任意一点，即y有n-5种取法.故这样的4圈共有（n-5）（n-3）个.

情形2∶x∈｛2,3｝且y/∈｛n+1,n+2｝.这时圈为CT（e）=（x,y,1,m）.对任意x，由于N′B（x）⊆｛n+1,n+2,n+3｝，所以y可取B｛n+1,n+2,n+3,m｝中的任意一个点，故这样的4圈共有2（n-4）个.

情形3∶x/∈｛2,3｝且y∈｛n+1,n+2｝.此时有CT（e）=（x,y,k,n+3）.对任意y，由于N′A（y）⊆｛1,2,3｝，所以x可取到A｛1,2,3,k｝中任何一个，所以这样的4圈共有2（n-4）个.

情形4∶x∈｛2,3｝且y∈｛n+1,n+2｝.此时CT（e）=（x,y,k,n+3,1,m）.由于只有边［2,n+1］和［3,n+2］属于E（G），所以这样的6圈恰有2个.

由于以上各情形中的圈CT（e）是互不相同的，因此由定义0.1知B中包含了2个6圈和n2-4n-1个4圈.

（2）假设G∗中某圈长为2l（l＞3），按G∗顶点的编号规则，将其最先编号为（1,n+2,2,n+ 3,3,···,n+l,l,n+1），所以在（⋆）式中取s=2,t=3.将k,m取适当点，则有

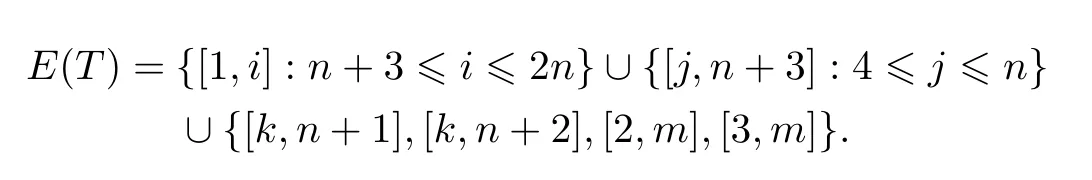
令B是T对应的FCB，e=［x,y］∈E（G）E（T），其中x∈A,y∈B.下面同样分4种情况讨论B中圈的长度及数量.

情形1∶x/∈｛2,3｝且y/∈｛n+1,n+2｝.这时圈为CT（e）=（x,y,1,n+3）.由于点1为度饱和点，所以x实际可取的点在点集A｛1,2,3,k｝中.若x=l，则n+1∈N′B（x），此时y有|｛n+4,n+5,···,2n｝|-1种取法；若x∈A｛1,2,3,l｝，每一个固定的x，y有|｛n+4,n+5,···,2n｝N′B（x）|个点可取.故这样的4圈共有（n-4）（n-5）+（n-4）=（n-4）2个.

情形2∶x∈｛2,3｝且y/∈｛n+1,n+2｝.此时圈为CT（e）=（x,y,1,m）.当x=2时，y有|B｛n+1,n+2,n+3,m｝|个点可取；当x=3时，y可取的点数为|B｛n+1,n+2,n+ 3,n+4,m｝|.所以这样的4圈共有2n-9个.

情形3∶x/∈｛2,3｝且y∈｛n+1,n+2｝.此时CT（e）=（x,y,k,n+3）.当y=n+1时，x可取A｛1,2,3,l,k｝中任何点；当y=n+2时，x可选A｛1,2,3,k｝中任意一点.所以这样的4圈共有2n-9个.

情形4∶x∈｛2,3｝且y∈｛n+1,n+2｝.此时有CT（e）=（x,y,k,n+3,1,m）.由于｛［2,n+1］,［3,n+1］,［3,n+2］｝⊆E（G），所以这样的6圈有3个.

故B中包含了3个6圈和n2-4n-2个4圈.

（3）在G∗只含4圈的情况下，由V（G∗）的编号知，第二个4圈为（3,n+4,4,n+3），所以在（⋆）式中取s=3,t=4.将k,m取适当点，则有

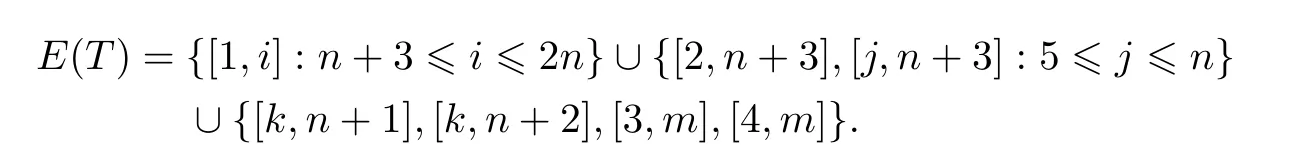
令B是T对应的FCB，e=［x,y］∈E（G）E（T），其中x∈A,y∈B.下面讨论B中圈的长度及数量.

情形1∶x/∈｛3,4｝且y/∈｛n+1,n+2｝.在此条件下，圈CT（e）=（x,y,1,n+3）.若x= 2，则y可取B｛n+1,n+2,n+3｝中任意点；若5≤x≤n，对每一个固定的x，y可取B｛n+1,n+2,n+3,N′B（x）｝中任一点.所以这样的4圈有（n-4）2+1个.

情形2∶x∈｛3,4｝且y/∈｛n+1,n+2｝.此时有CT（e）=（x,y,1,m）.若取定任一x，则y有|B｛n+1,n+2,n+3,n+4,m｝|种取法，所以这样的4圈有2（n-5）个.

情形3∶x/∈｛3,4｝且y∈｛n+1,n+2｝.此时CT（e）=（x,y,k,n+3）.取定y，x可以在集合A｛1,2,3,4,k｝中任意选取，故这样的4圈有2（n-5）个.

情形4∶x∈｛3,4｝且y∈｛n+1,n+2｝.此时CT（e）=（x,y,k,n+3,1,m）.由于｛［3,n+ 1］,［3,n+2］,［4,n+1］,［4,n+2］｝⊆E（G），所以这样的6圈有4个.

因此，B中包含了4个6圈和n2-4n-3个4圈.

引理1.2设图G是2n阶（n-2）-正则二部图（n≥ 10），B∗是G的一个MFCB，T为B∗对应的生成树，则T不含长为6的路.

证明反证法，假设T含长为6的路，不妨设为P=a1b1a2b2a3b3a4.不失一般性，设｛a1,a2,a3,a4｝⊆A，｛b1,b2,b3｝⊆B.在T中去掉P中所有的边，则会产生7个连通分支.对x∈V（P），记x所在的连通分支为Tx.令由于n≥10，故W非空.为了证明结论成立，首先证明下面的断言.

断言B∗中至少含有|W|个长度大于等于6的圈.

因为W非空，所以W至少与T-E（P）的一个连通分支有公共顶点.

若V（Tb1）∩W≠∅.对于∀β∈V（Tb1）∩W，由于T是树，所以进一步有而［β,a4］∈E（G），所以圈CT（［β,a4］）∈B∗且长度大于等于8.因为β可以取W中任意一点，故B∗中形如的圈至少有|∩W|个.同理可证，若不妨设则B∗中形如圈CT（［β,a1］）的数量不少于|V（Tb3）∩W|个.

由上面的讨论知，B∗中至少含有|V（T）∩W|=|W|个长度大于等于6的圈.

定理1.1设图G为2n阶（n-2）-正则二部图，T为G的最小基本圈基对应的生成树，则T同构于T1,T2,T3（见图1）.

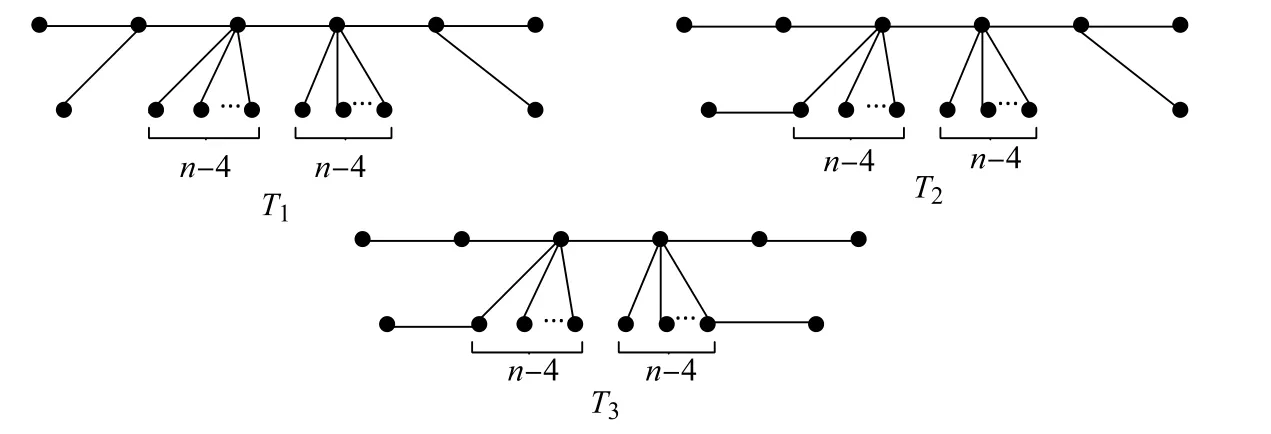
图1　生成G的MFCB的树Fig.1　Trees which produce MFCB of G

证明由引理1.2知，T的直径不超过5.假设T中最长路的长度为4，不妨设为P′= abcde，显然c在另一部中的不邻点不在T上，这与T是G的生成树矛盾.故T的直径为5.

设T中最长路为P=a1b1a2b2a3b3.不失一般性，设｛a1,a2,a3｝⊆A，｛b1,b2,b3｝⊆B. T-E（P）含有6个连通分支，对x∈V（P），记x所在的连通分支为Tx.

由于P是最长路.所以，Ta1,Tb3为孤立点，Tb1,Ta3分别为以b1和a3为中心的星图，并且对于和有

由以上分析知∶∀β∈B，dT（a2,β）≤3；∀α∈A，dT（b2,α）≤3.

下证d3（a2）=2，d3（b2）=2.

由于T为二部图，故到a2距离为3的点都在B中，到b2距离为3的点都在A中.设则有dT（a2,β1）=3，dT（a2,β2）=3；设则有dT（b2,α1） =3，dT（b2,α2）=3.于是有d3（a2）≥2，d3（b2）≥2.

假设∃β3∈B｛β1,β2｝，使dT（a2,β3）=3，显然或不失一般性，设则对于s∈｛α1,α2｝，t∈｛β1,β2,β3｝，有dT（s,t）=dT（s,b2）+dT（b2,t）=5.由于α1和α2在｛β1,β2,β3｝中至多各有一个不邻点，不妨分别取为β1，β2.考察G∗中α1,α2, β1,β2,a2,b2间的相邻关系可知G∗含有大于4的圈，并且｛［α1,β2］,［α1,β3］,［α2,β1］,［α2,β3］｝⊆E（G），所以圈基中至少含有4个6圈.这与引理1.1矛盾，于是d3（a2）=2，d3（b2）=2.

综合以上结论，我们得到G的最小基本圈基的生成树同构于T1,T2,T3.

定理1.2对任意2n阶（n-2）-正则二部图G（n≥10），

（1）若G∗含6圈，则G的MFCB由2个6圈和n2-4n-1个4圈组成；

（2）若G∗含长度大于6的圈（不含6圈），则G的MFCB由3个6圈和n2-4n-2个4圈组成；

（3）若G∗只含4圈，则G的MFCB由4个6圈和n2-4n-3个4圈组成.

证明在与定理1.1相同的记号下，图G中α1,α2在｛β1,β2｝中至少各存在一个邻点，故G的MFCB中至少含有2个6圈.记|E（G［α1,α2,β1,β2］）|=q，显然q∈｛2,3,4｝.

情形1∶q=2.考察G∗中α1,α2,β1,β2,a2,b2间的相邻关系可知，（α1,b2,α2,β1（β2）,a2, β2（β1））是G∗中的一个6圈.这时T∪E（G［α1,α2,β1,β2］）为G的MFCB贡献仅有的两个6圈.这说明，若G∗含6圈，总可以对G的顶点进行适当地编号生成树T，其对应的MFCB只含2个6圈，且其余圈为4圈.

情形2∶q=3.仍然考察G∗中α1,α2,β1,β2,a2,b2间的相邻关系，知G∗中含有长度大于6的圈.若G∗中存在6圈，我们总可以经过适当编号有情形1的结果，所以我们限制G∗不含6圈.由于T∪E（G［α1,α2,β1,β2］）中含有3个6圈，故G的MFCB只含3个6圈.这就是说，若G∗不含6圈，含有长度大于6的圈，总可以对G的顶点进行适当地编号生成树T，其对应的MFCB含3个6圈和n2-4n-2个4圈.

情形3∶q=4.不难得出G∗只含4圈.否则，若含长度大于4的圈，我们总可以经过适当编号有情形1或情形2的结果.此时G的MFCB中含有4个6圈.因此，若G∗只含4圈，总可以对G的顶点进行适当地编号生成树T，其对应的MFCB含4个6圈和n2-4n-3个4圈.

［1］LIEBCHEN C，RIZZI R.Classes of cycle bases［J］.Discrete Appl Math，2007，155（3）：337-355.

［2］HORTON J D.A polynomial-time algorithm to find the shortest cycle basis of a graph［J］.SIAM J Computing，1987，16：359-366.

［3］BRADSHAW Z，JARADAT M M M.Minimum cycle bases for direct products ofK2with complete graphs［J］. Australas J Combin，2009，43：127-131.

［4］HAMMACK R.Minimum cycle bases of direct products of complete graphs［J］.Inform Process Lett，2007，102（5）：214-218.

［5］STADLER P.Minimum cycle bases of Halin graphs［J］.J Graph Theory，2003，43（2）：150-155.

［6］KAVITHA T，LIEBCHEN C，MEHLHORN K，et al.Cycle bases in graphs characterization，algorithms，complexity，and applications［J］.Comput Sci Rev，2009，3（4）：199-243.

［7］GHAREGHANI N，KHOSROVSHAHI G B.Minimum cycle basis of direct product ofK2×Kn［J］.Linear Algebra Appl，2014，458：671-678.

［8］BONDY J A，MURTY U S R.Graph Theory with Applications［M］.New York：Macmilan Ltd Press，1976.

［9］LU M.Spectral radius and Hamiltonian graphs［J］.Linear Algebra Appl，2012，437：1670-1674.

（责任编辑：李艺）

Minimum fundamental cycle basis of（n-2）-regular bipartite graphs with order 2n

HE Chang-xiang，LIU Wei-long
（College of Science，University of Shanghai for Science and Technology，Shanghai200093，China）

Let G be an（n-2）-regular bipartite graph with order 2n.In this paper，we constructed a fundamental cycle basis of G and proved this basis is a minimum fundamental cycle basis.For any minimum fundamental cycle basis，we also determined the structure of the spanning tree corresponding to it.

regular bipartite graph；cycle basis of graph；minimum cycle basis；minimum fundamental cycle basis

O157.5

A

10.3969/j.issn.1000-5641.2016.02.008

1000-5641（2016）02-0056-06

2015-04

国家自然科学基金（11201303，11301340）；上海市自然科学基金（12ZR1420300）

何常香，女，副教授，硕士生导师，研究方向为代数图论.E-mail：changxiang-he@163.com.