Plate方程时间依赖全局吸引子的存在性

刘亭亭，马巧珍

（西北师范大学 数学与统计学院，兰州　730070）

Plate方程时间依赖全局吸引子的存在性

刘亭亭，马巧珍

（西北师范大学 数学与统计学院，兰州730070）

时间依赖全局吸引子的概念是Di Plinio，Temam等人于近期提出的.在非线性项f满足临界增长条件时，应用算子分解技巧，验证了系数参数与时间t有关时plate方程对应的过程族｛U（t，τ）｝的渐近紧性，进而获得了plate方程时间依赖全局吸引子的存在性及正则性.

plate方程；时间依赖全局吸引子；渐近紧性；正则性

0　引　言

令Ω⊂Rm（m≥5）是具有光滑边界的有界区域，本文考虑下面的问题∶其中u=u（x,t）为Ω×（τ,+∞）上的未知变量，ε（t）是关于t的函数，α＞0是阻尼系数，g∈L2（Ω），ε和f（u）分别满足下面的条件.

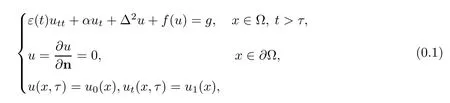
（1）函数ε∈C1（R）满足

特别地，存在L＞0，使得

（2）函数f∈C2（R）,f（0）=0,并且

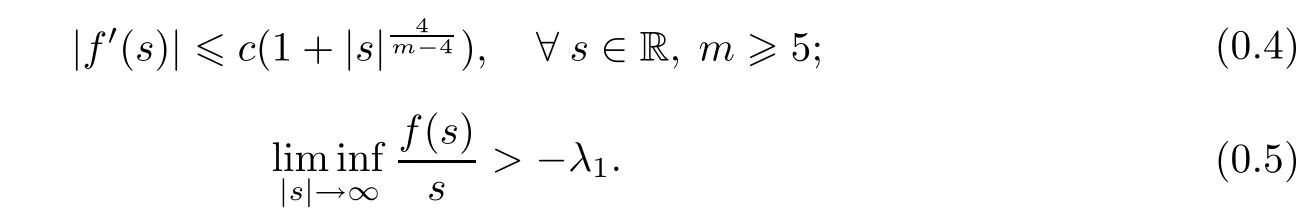
这里λ1＞0是A=Δ2的第一个特征值，D（A）=是常数，其中符号⋐表示嵌入是紧的.

时间依赖全局吸引子是由Di Plinio，Temam等人在文［1-3］中提出的，并分别讨论了振动方程与波方程时间依赖全局吸引子的存在性及正则性.受文［1-3］的启发，本文考虑plate方程时间依赖全局吸引子的存在性及正则性.plate方程源自Woinowsky-Krieger所建立的弹性振动方程［4］.不过这类问题的严格数学分析及解的整体存在性及渐近性的研究始于Ball在文［5］中关于弹性梁方程稳定性的讨论.近几年，针对plate方程整体吸引子的研究引起了大家的广泛兴趣，比如∶在文［6-8］中作者研究了当ε（t）=1时，plate方程在无界区域中全局吸引子的存在性.文［9-10］中，作者分别讨论了有界域上具有非线性阻尼和临界非线性项的自治plate方程和非自治plate方程在弱拓扑空间中紧吸引子的存在性.文［11］中，作者研究了带加性噪声的随机plate方程随机吸引子的存在性.

对于方程（0.1），当ε=ε（t）时plate方程吸引子的存在性还未见讨论.本文借助文［2］中的方法，研究plate方程（0.1）在非线性项满足临界指数增长条件时，时间依赖全局吸引子的存在性及正则性.

1　预备知识

与文［2］类似，记H=L2（Ω），对应的内积与范数分别记为〈·,·〉,‖·‖.对于0≤σ≤2，定义由A生成的Hilbert空间族Hσ=dom（Aσ4），并赋予如下内积与范数

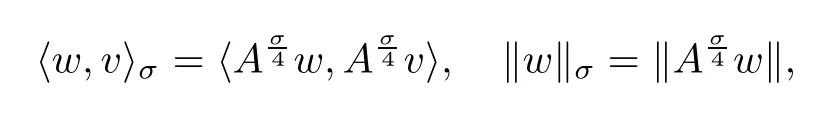
特别地，有紧嵌入Hσ+1⋐Hσ.

对t∈R及0≤σ≤2，引入时间依赖空间

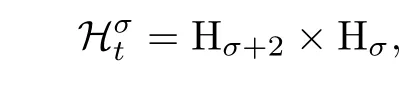
对应的时间依赖范数为

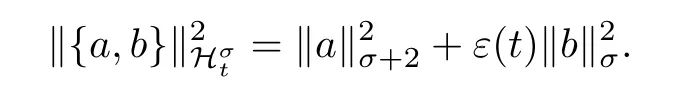
当σ=0时，通常记Ht=H2×H，对应的范数为由紧嵌入Hσ+1⋐Hσ,显然当0≤σ≤2时，有以下紧嵌入成立.

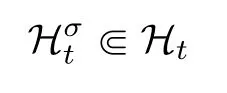
令

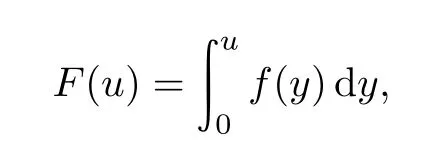
由（0.5）式，我们可以得到

引理1.1［2］对于任意的0＜ν＜1和常数c1、c2≥0，下面的不等式成立∶

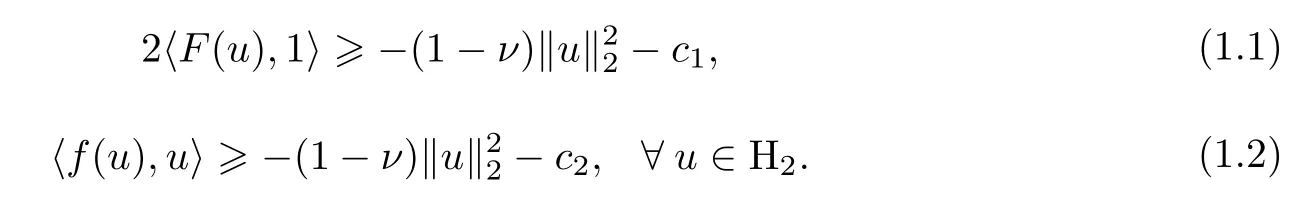
2　主要结论与证明

2.1先验估计

对于问题（0.1）解u的存在性，可以通过标准的Galerkin方法［12］得到，并且它的解满足∶在任意区间［τ,t］上，

由此，可以定义下面的过程族

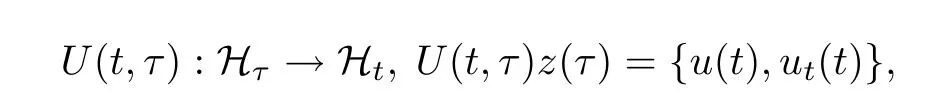
其中z（τ）∈Hτ,u是问题（0.1）的唯一解.

引理2.1假设条件（0.2）-（0.5）成立，问题（0.1）生成的过程族U（t,τ）∶Hτ→Ht,t≥τ∈R，满足下面的性质∶对每个初值zi（τ）∈Hτ并且‖zi（τ）‖Hτ≤R,i=1,2,成立

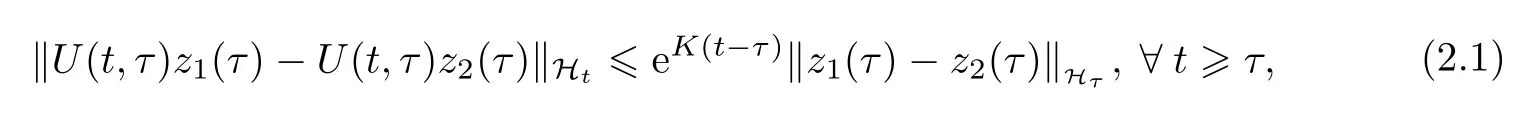
其中常数K=K（R）＞0.

为了证明引理2.1，我们先证明下面的结论.

引理2.2假设条件（0.2）-（0.5）成立，对z（τ）∈Hτ,记U（t,τ）z（τ）是问题（0.1）关于初始时刻τ和初始值z（τ）的解，则存在K≥0，使得

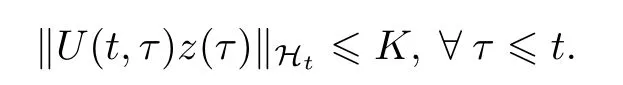
证明令

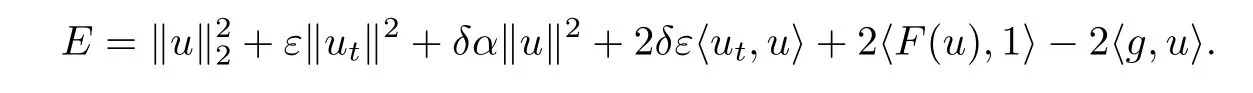
用2ut+2δu与（0.1）在L2中做内积可得

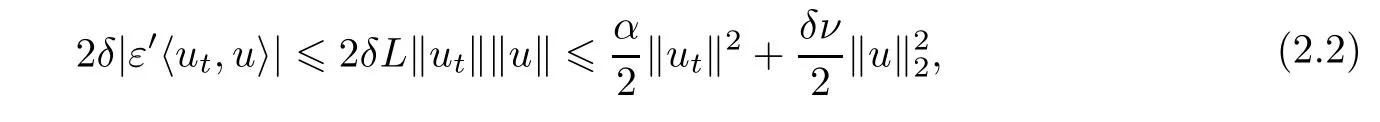
把（2.2）代入上式，得到

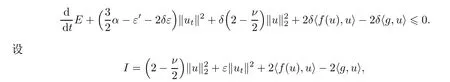
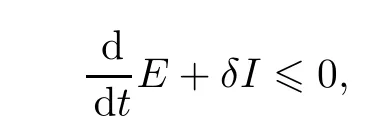
因此有

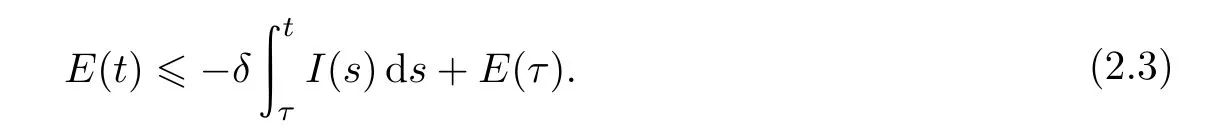
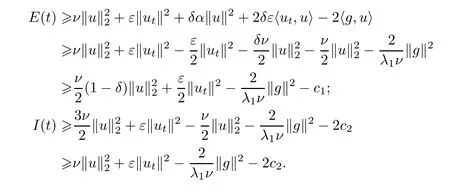
由1-δ＞0，存在一个正常数C1，使得

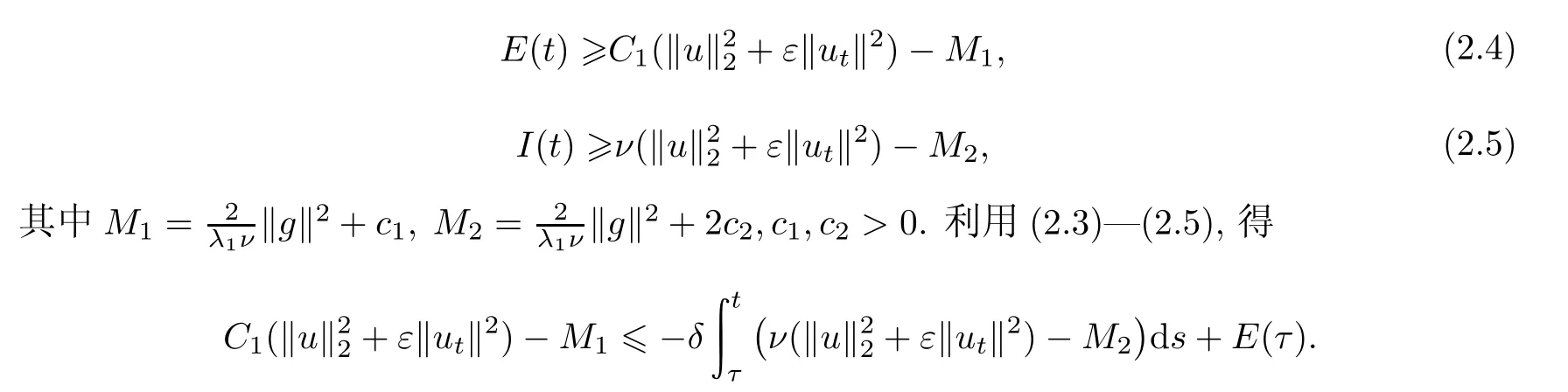
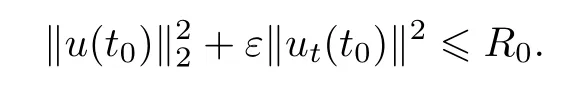
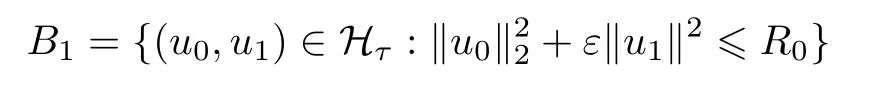
是有界吸收集.因此B0也是过程族｛U（t,τ）｝的有界吸收集.

为了描述方便，下文中出现的正常数C，在每一行甚至同一行中的取值都可能是不同的.

引理2.1的证明取z1（τ）,z2（τ）∈Hτ，并且设C＞0是与R有关而与zi（τ）无关的常数.在引理2.2中的能量估计保证了下面的不等式∶

定义｛ui（t）,∂tui（t）｝=U（t,τ）zi（τ）并且令¯z（t）=｛（t）,t（t）｝=U（t,τ）z1（τ）-U（t,τ）z2（τ）.因此，这两个解的差关于初始值（τ）=z1（τ）-z2（τ）满足方程

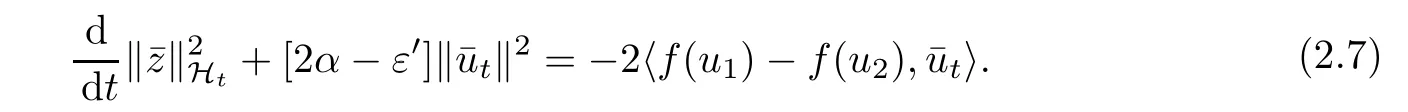
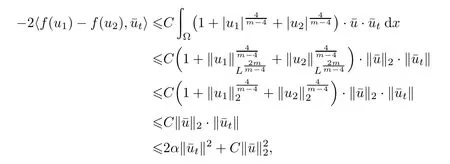
将上式代入（2.7），计算后得

在［τ,t］上利用Gronwall引理，可得

其中C≥0是与R有关的常数.

记Bt（R）=｛z∈Ht∶‖z‖Ht≤R｝.

引理2.3假设条件（0.2）-（0.5）成立，则存在一个R0＞0使得B=｛Bt（R0）｝是过程族｛U（t,τ）｝的时间依赖吸收集，并且对M0≥R0，有

证明由引理2.2及文［1-2］，易得结论成立.

2.2时间依赖全局吸引子的存在性

定理2.1［2］如果过程U（t,τ）是渐近紧的，则时间依赖全局吸引子存在并且唯一.

2.2.1算子分解

将f分解为f=f0+f1,这里f0,f1∈C2（R），且对某个k≥0满足∶

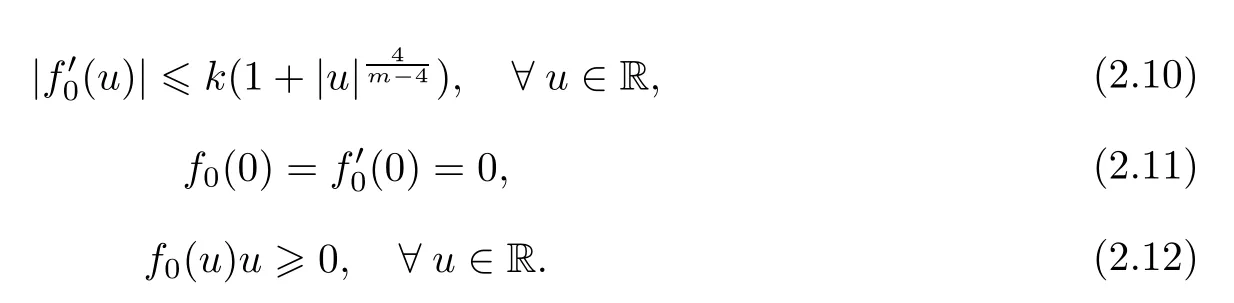
由引理2.3知B=｛Bt（R0）｝t∈R是一个时间依赖吸收集.因此，对任意的z（τ）∈Bτ（R0），U（t,τ）z（τ）分解为

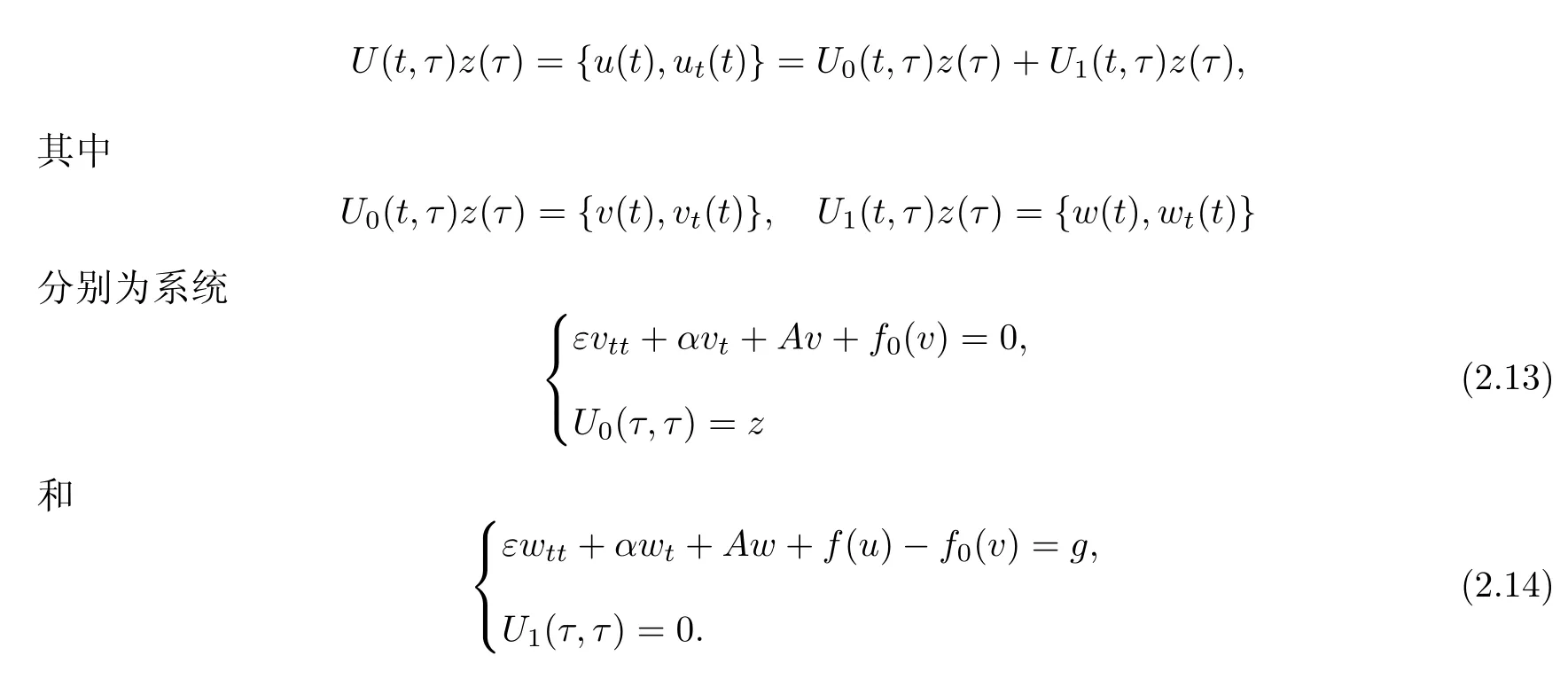
的解.

在以下过程中，常数C≥0只与B有关.

引理2.4存在δ=δ（B）＞0，使

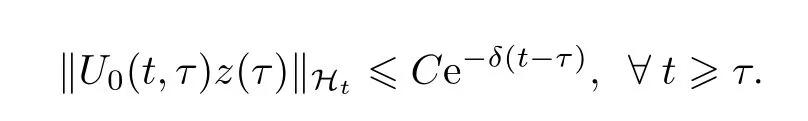
证明首先，我们有

定义泛函∶

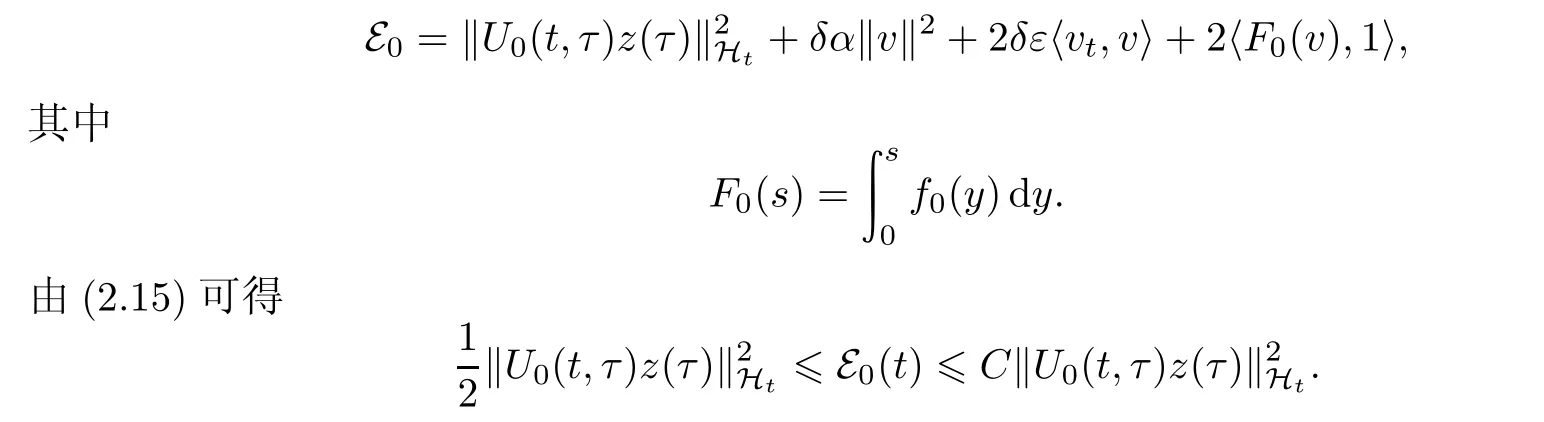
用2vt+2δv与（2.13）在L2中做内积，可得

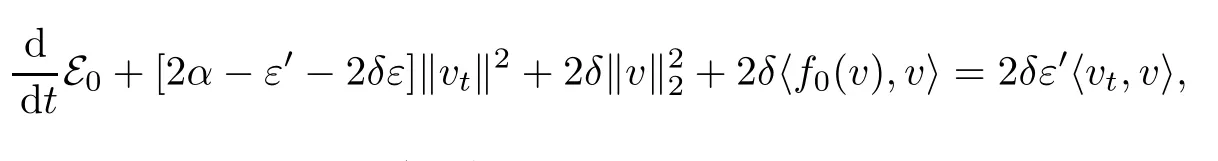
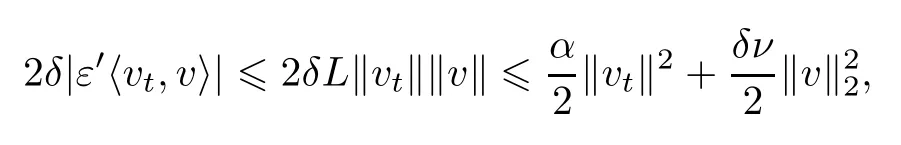
再由条件（2.12），可以得到

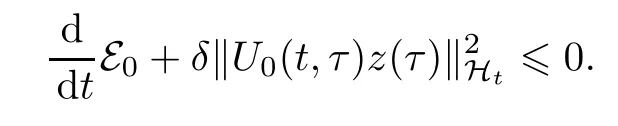
利用Gronwall引理即得结果成立.

由以上证明可知，下面的估计式成立

引理2.5存在M=M（B）＞0，使得

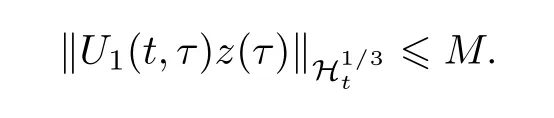
证明取足够小的δ＞0和足够大的C＞0，令

且

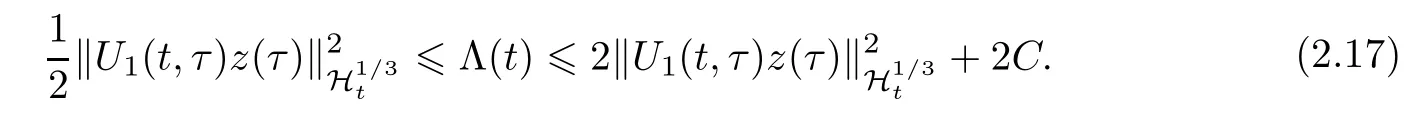
由（2.16）和f的增长性条件及嵌入不等式，有

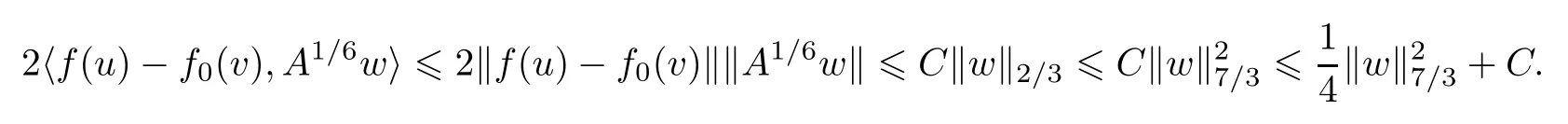
用2A1/6wt+2δA1/6w与（2.14）在L2中做内积，得到

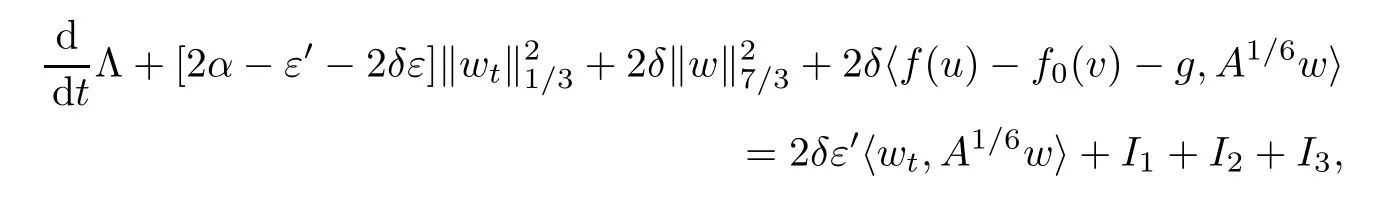
其中

因此，对足够小的δ＞0，有

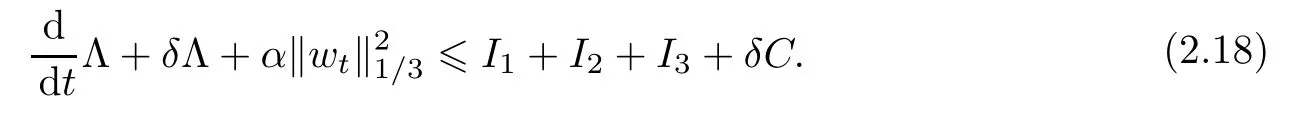
得到

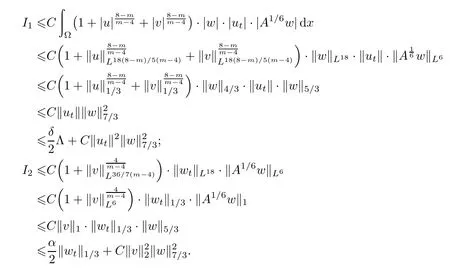
结合（2.9），有

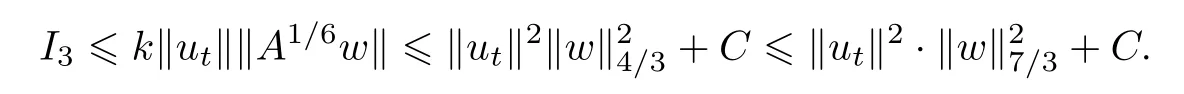
将以上不等式代入（2.18），得

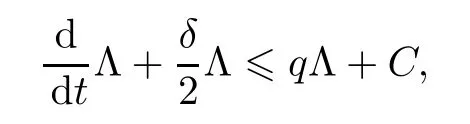
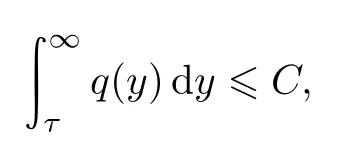
并且

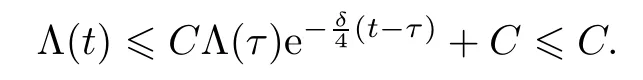
再结合（2.17），得到U1（t,τ）z（τ）在空间中有界.

2.2.2不变吸引子的存在

定理2.2假设条件（0.2）-（0.5）成立，则问题（0.1）生成的过程族U（t,τ）∶Hτ→Ht在 Ht中拥有不变的时间依赖全局吸引子

证明根据引理2.5,考虑族R=｛Kt｝t∈R,其中

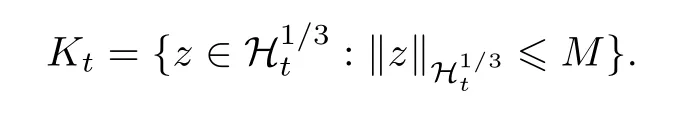
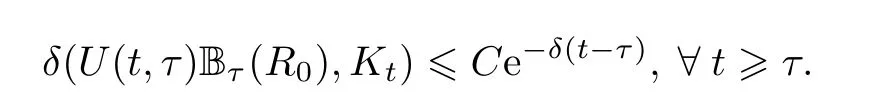
因此过程族｛U（t,τ）｝是渐近紧的，由定理2.1知，时间依赖全局吸引子存在并且唯一.根据引理2.1知，过程｛U（t,τ）｝是强连续的，由文［2］中的定理5.6知是不变的.

2.3吸引子的正则性

定理2.3假设条件（0.2）-（0.5）成立，则问题（0.1）的时间依赖吸引子｛At｝t∈R在中有界，且界与时间t无关.

为了证明定理2.3,固定τ∈R,z（τ）∈Aτ，把U（t,τ）z（τ）分解为U3（t,τ）z（τ）与U4（t,τ）z（τ）的和，其中U3（t,τ）z（τ）=｛v（t）,vt（t）｝和U4（t,τ）z（τ）=｛w（t）,wt（t）｝，它们分别对应系统

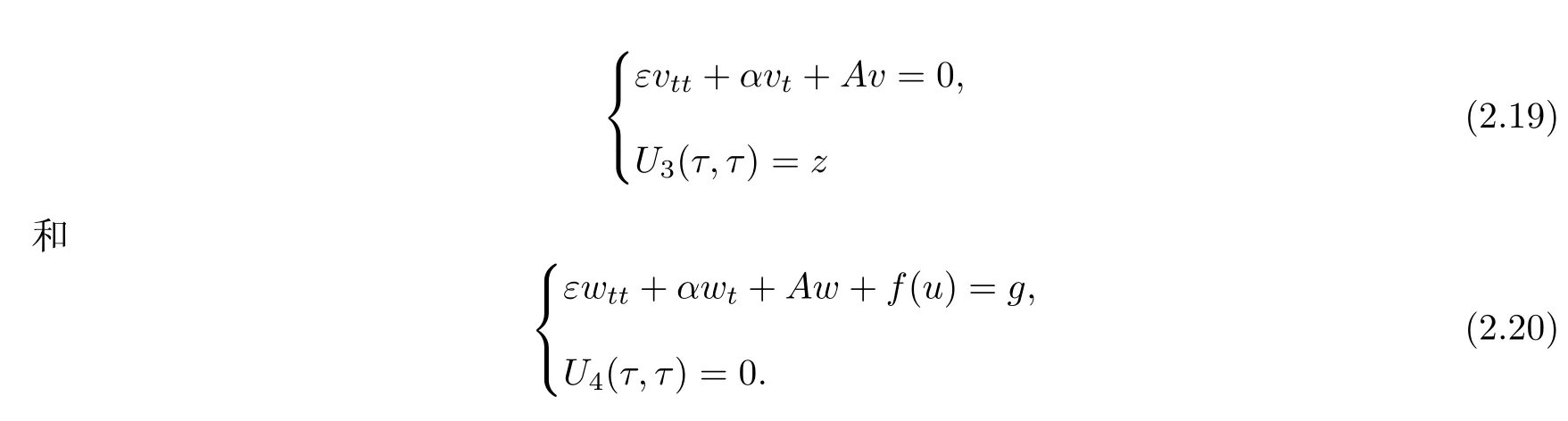
作为引理2.4的特殊情况，显然有

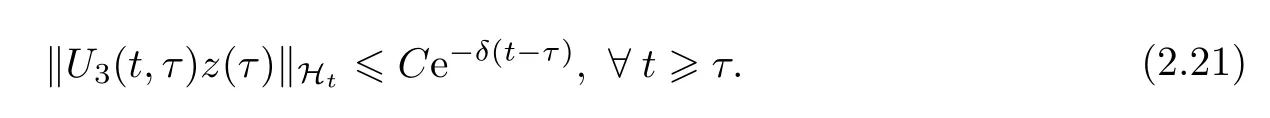
引理2.6对M1=M1（A），成立

证明令

对足够小的δ＞0和足够大的c≥0（依赖于‖g‖），有

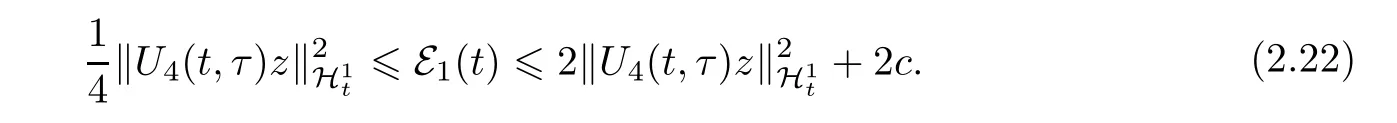
用2A1/2wt+2δA1/2w与（2.20）在L2中做内积，有

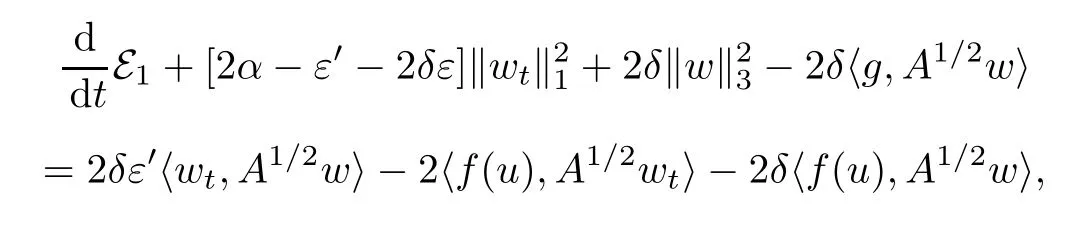
令δ足够小，通过计算有

其中C＞0是与At在中的界有关的常数.由（2.16），及嵌入5）,得到

因此

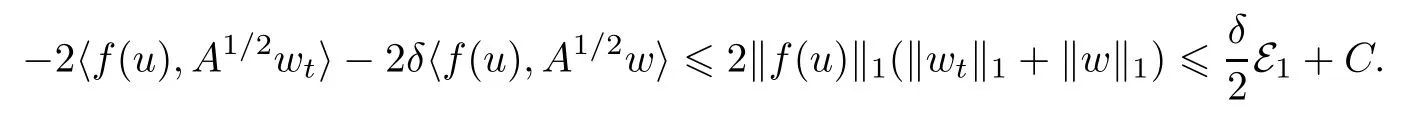
从而

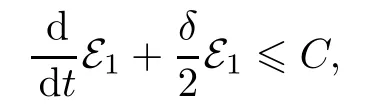
定理2.3的证明令

由不等式（2.21）和引理2.6，对t∈R，有

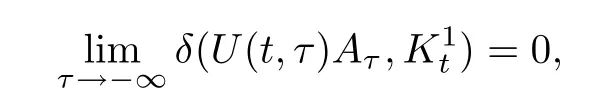
其中

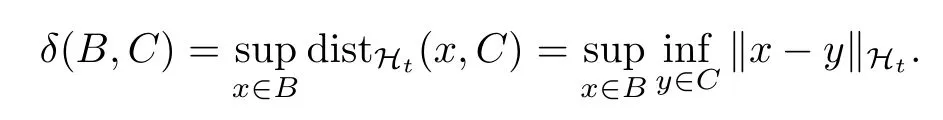
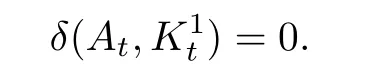
［1］DI PLINIO F，DUANE G S，TEMAM R.Time-dependent attractor for the oscillon equation［J］.Discrete Contin Dyn Syst，2011，29：141-167.

［2］CONTI M，PATA V，TEMAM R.Attractors for processes on time-dependent spaces：Applications to wave equations［J］.J Differential Equations，2013，255：1254-1277.

［3］DI PLINIO F，DUANE G S，TEMAM R.The 3-dimensional oscillon equation［J］.Boll Unione Mat Ital，2012，5（1）：19-53.

［4］WOINOWSKY-KRIEGER S.The effect of axial force on the vibration of hinged bars［J］.J Appl Mech，1950，17：35-36.

［5］BALL J M，LAX D.Initial-boundary value problems for an extensible beam［J］.J Math Anal Appl，1973，42：61-90.

［6］KHANMAMEDOV A K.Existence of a global attractor for the plate equation with a critical exponent in an unbounded domain［J］.Appl Math Lett，2005，18：827-832.

［7］KHANMAMEDOV A K.Global attractors for the plate equation with a localized damping and a critical exponent in an unbounded domain［J］.J Differential Equations，2006，225：528-548.

［8］XIAO H B.Asymptotic dynamtics of plate equations with a critical exponent on unbounded domain［J］.Nonl Anal，2009，70：1288-1301.

［9］YANG L，ZHONG C K.Global attractor for plate equation with nonlinear damping［J］，Nonl Anal，2008，69：3802-3810.

［10］YANG L.Uniform attractor for non-autonomous plate equation with a localized damping and a critical nonlinearity［J］.J Math Anal Appl，2008，338（2）：1243-1254.

［11］MA W J，MA Q Z.Attractors for stochastic strongly damped plate equations with additive noise［J］.Electron J Differential Equations，2013，12（3）：1501-1526.

［12］BABIN A V，VISHIK M I.Attractors of Evolution Equations［M］.Amsterdam：North-Holland，1992.

（责任编辑：林磊）

Existence of time-dependent global attractors for plate equations

LIU Ting-ting，MA Qiao-zhen
（College of Mathematics and Statistics，Northwest Normal University，Lanzhou730070，China）

The concept of time-dependent global attractors was recently presented by Di Plinio，Temam et al.By using the skill of the operator decomposition，the asymptotic compactness of a family process｛U（t，τ）｝corresponding to the plate equations with the coefficient dependent on time was proved，and then the existence of time-dependent global attractors as well as the regularity were obtained under the condition that f satisfies the critical exponent growth.

plate equation；time-dependent global attractor；asymptotic compactness；regularity

O175.29

A

10.3969/j.issn.1000-5641.2016.02.005

1000-5641（2016）02-0035-10

2015-04

国家自然科学基金（11561064）；甘肃省自然科学基金（1107RJZA223）；甘肃高校科研项目

刘亭亭，女，硕士研究生，研究方向为无穷维动力系统.E-mail：1171638929@qq.com.

马巧珍，女，教授，博士生导师，研究方向为应用微分方程与无穷维动力系统. E-mail：maqzh@nwnu.edu.cn.