方位俯仰跟踪框架下的角偏差无奇点修正方法

陈嘉鸿，向颉，王二建

（中国卫星海上测控部飞行器海上测量与控制联合实验室，江苏江阴214431）

方位俯仰跟踪框架下的角偏差无奇点修正方法

陈嘉鸿，向颉，王二建

（中国卫星海上测控部飞行器海上测量与控制联合实验室，江苏江阴214431）

分析回顾了雷达工程中，当前通用的方位俯仰极坐标框架下，无线电雷达跟踪测量系统角偏差正割补偿修正方法的由来及其局限性；提出了跟踪指向坐标系的定义。利用坐标转换原理给出了一种简便易行的偏差无奇点精确修正推导新方法，并证明了新方法与通用的基于立体几何推理方法的等价性，同时分析了新方法在雷达轴系偏差修正中的典型应用及其对系统跟踪测量精度的影响。对于89°仰角、方位俯仰角偏差均为3 mrad的情形，正割补偿修正法指向计算存在6 759.2"的方位角误差和63.5"的俯仰误差。新的推理方法有利于极坐标框架下的空间目标高精度跟踪与测量，尤其是高仰角过顶跟踪性能、指向精度和跟踪数据利用率的提高。

雷达工程；跟踪测量；极坐标框架；偏差修正；正割补偿

0　引言

在空间飞行器测量技术领域，目标跟踪与定位是重要的任务之一。角度测量和修正的精度直接影响目标跟踪与定位的精度。

方位-俯仰型角度跟踪测量系统一般是指利用方位轴和俯仰轴组合调整，使无线电雷达电轴或光学系统的光轴指向目标，从而实现对目标跟踪测量的系统。由于方位-俯仰型天线座结构紧凑、旋转关节少、刚度强，伺服控制系统容易实现，其原理简单、实施方便，被工程及学术界普遍应用［1-8］。但其工程应用中常用的角偏差修正正割补偿算法奇异性问题也很明显，主要表现为在俯仰角接近90°时，会出现无穷大的修正量，导致角度测量误差急速变大；工程应用中高仰角（一般超过75°时）测量值经常被舍弃，难以有效利用；目标过顶跟踪时的盲区问题在正割补偿框架下俯仰角接近90°时恶化严重，且难以克服［9-14］；同时，其基于立体几何的数学推导过程较复杂［1-8］。

从查阅到的文献看，较早角度偏差修正的研究大都通过几何推理获得近似的正割补偿修正方法［5-8］，多年来已形成了成熟的应用，Samuel等［1］、刘利生［2］、钟德安［3］、李淼等［4］将之作为经典方法不仅应用于动态跟踪过程中的偏差修正，也应用于测量设备轴系偏差的修正。较近的与此相关的研究主要是基于该正割补偿法对应用系统进行改进，其中文献［9-14］主要集中于设备跟踪过顶问题的研究，文献［15-16］主要针对系统跟踪问题重点开展了跟踪稳定性研究，文献［17-19］侧重于对角误差估计方法和模型的研究。

文献［20］在研究测量精度问题中，基于坐标转换，提出了光学与无线电雷达捷联测量新方法。为了提高方位-俯仰型角度跟踪测量系统特别是大型空间目标测量雷达和光学望远镜的高仰角测量精度和数据利用率，本文重点针对当前通用的偏差正割补偿修正方法的奇异性问题开展研究，基于指向坐标系的定义，从坐标转换的角度给出一种严格、简洁的修正方法，并从理论上证明了其精确性和准确性，便于工程应用中的偏差修正和高仰角跟踪能力的提高。

1　正割补偿修正方法分析

一般的光学测量系统偏差称为脱靶量，无线电雷达测量系统偏差称为动态滞后。众多文献［1-8］对光学测量系统的轴系偏差修正给出了很详细的推理和分析，无线电雷达测量系统偏差修正则是直接对简化公式的应用。

1.1光学脱靶量修正

以光学经纬仪测量系统为例，脱靶量ΔA、ΔE，反映在像面（摄像机靶面）上就是偏离视场中心的距离ΔX、ΔY，根据立体几何原理，有如下关系（具体推导过程参见文献［2-3］）:

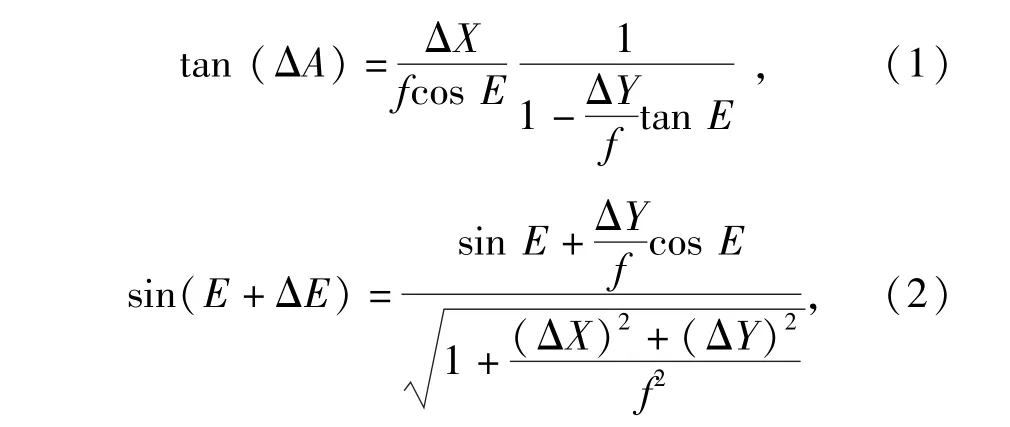
式中:f为经纬仪焦距；A、E分别为光轴指向的方位角和俯仰角。

考虑ΔA、ΔE值很小，经泰勒展开忽略高阶项可得

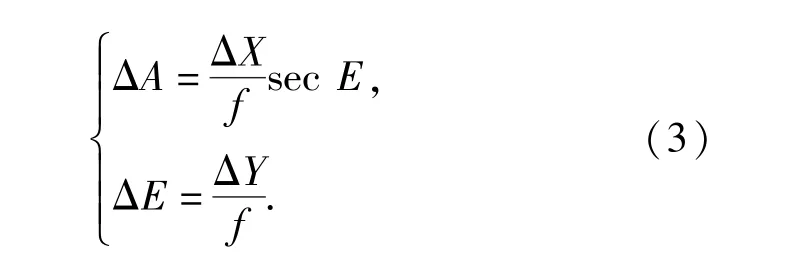
工程应用中常用（3）式，其实质是一个近似表达式。

1.2雷达动态滞后修正

由于雷达跟踪的基本原理是偏差跟踪，即驱动天线使目标像点（或信号中心）趋近雷达中心；同时由于噪声的影响，以及无线电雷达天线伺服系统速度、加速度有限，实际跟踪过程中总是存在目标像点与雷达中心的偏差，传统上称之为动态滞后。计算目标的实际指向时一般都需要对此动态滞后量进行修正。

一般的雷达动态滞后直接测量值是方位俯仰误差电压ΔUA、ΔUE，记其定向灵敏度分别为KA、KE，根据误差角定义为

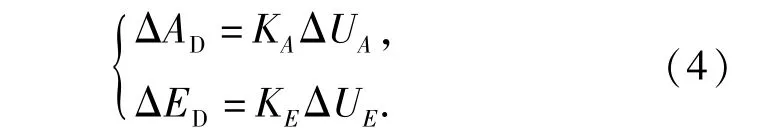
对比（3）式，其中，tan（ΔAD）与ΔX/f，tan（ΔED）与ΔY/f各自等价。由于ΔAD、ΔED为接近0的小量，大多数文献均直接给出或应用雷达角偏差的正割补偿计算方法为

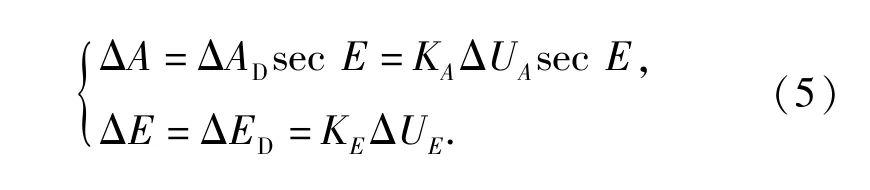
（5）式的物理意义本质上与（3）式一致，也是一个近似表达。

1.3轴系偏差修正

无线电设备轴系偏差较为复杂，包括大盘不水平（方位轴不垂直于基准平面）、两轴不正交（俯仰轴不垂直于方位轴）、电轴不垂直（即电轴不垂直于俯仰轴）等。如果无线电雷达设备借助光学设备进行标定，则还包括光机偏差Sb（光轴不垂直于俯仰轴）、光电偏差（电轴不平行于光轴），二者综合起来等效于电轴不垂直于俯仰轴。其中电轴不垂直与光机偏差的物理意义一致，本文以此为例进行分析说明。

依据文献［2-3］，电轴/光轴不垂直或光机偏差只引起方位角误差ΔAb.如图1所示，当仰角E抬高时电轴本应沿大圆弧QO移动。因为有电轴不垂直角Sb，电轴却沿Q′O′移动，在仰角为E时电轴指向S′，产生横向角误差SS′（即Sb，对应大圆弧SS′），投影至方位转盘（类似于赤道面）上为QQ"，即对应方位角误差为

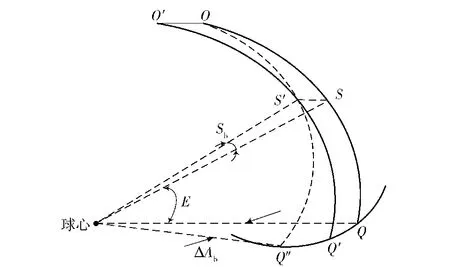
图1　光机偏差引起的方位误差Fig.1 Azimuth error caused by offset between optical axis and mechanical axis

上述分析成立的前提是当且仅当大圆弧SS′与仰角E上半径为R cos E的小圆弧SS′弧长相等时才成立（类似于纬度圈），其中R为球半径。事实上这二者是不可能相等的。因此（6）式也是一个近似表达。

1.4极限状态分析

从（3）式、（5）式以及（6）式可以看出，无论跟踪误差或光电偏差多么小，在仰角E趋近90°的过程中，方位角修正量ΔA均会超过180°趋向无穷大，从而出现奇异性问题。此时修正值的物理意义不再明确。因为在仰角趋近90°的过程中，从实际天线连续旋转的意义上分析，方位角极限修正量不会超过180°，且为仰角E的连续单调量，无穷大的修正量是无意义的。

由于实际工程应用中跟踪偏差和轴系误差始终存在，正割补偿修正方法在高仰角时将会导致计算的修正量与真值修正量差异较大，严重时计算的修正量不可用；基于同样的原因，高仰角跟踪也会出现计算的修正量远大于实际需要的角度调整量，从而导致天线不必要的转动，已有的跟踪性能不能得到充分利用。

2　偏差无奇点修正方法

当前通用的光学或无线电雷达跟踪测量主要基于地平坐标系和设备测量坐标系，如果需要计算惯性空间的位置，则还需要用到惯性坐标系。虽然光学设备与无线电雷达设备误差跟踪原理和修正方法是一致的，但雷达测量误差修正不如光学测量那样便于理解，本文侧重于以雷达测量为例进行修正方法的讨论，并对与光学测量的等价性进行必要的说明。

跟踪测量设备的方位角、俯仰角、距离一般定义在设备测量坐标系下，且跟踪误差也在同样的坐标系下进行分析和修正量解算。众所周知，坐标系转换的原理简单易懂。本文尝试从坐标系转换原理出发研究新的偏差无奇点修正推理方法。

2.1坐标系定义

2.1.1雷达测量坐标系OMXMYMZM

原点为雷达三轴中心，XM轴在方位大盘平面内，指向方位角为0°的方向；YM轴垂直方位大盘平面，平行于方位轴（方位逆时针旋转的轴向）；ZM轴由右手螺旋法则确定。

本文约定测量坐标系下方位顺时针旋转为正，范围是0°～360°；俯仰抬高为正，范围是0°～180°，对于可负仰角跟踪的系统，可以根据需求定义为-n～（180+n）°。类似的光学测量坐标系与此定义一致。

2.1.2雷达指向坐标系ODXDYDZD

一般光学测量可以建立以光学中心为原点，光轴为x轴，成像靶面分别为y轴和z轴的指向坐标系，如星敏感器坐标系。类似可以建立雷达指向坐标系，原点为雷达三轴中心，XD轴为电轴，目标方向为正；ZD轴指向俯仰旋转轴，面向目标，向右为正（即正镜时俯仰角抬高的右手旋转方向为正）；YD轴由右手螺旋法则确定，指向俯仰旋转的切向方向，逆时针为正。

当雷达天线方位角、俯仰角均为0°且不考虑轴系安装误差时，OMXMYMZM与ODXDYDZD重合。两坐标系关系如图2所示。

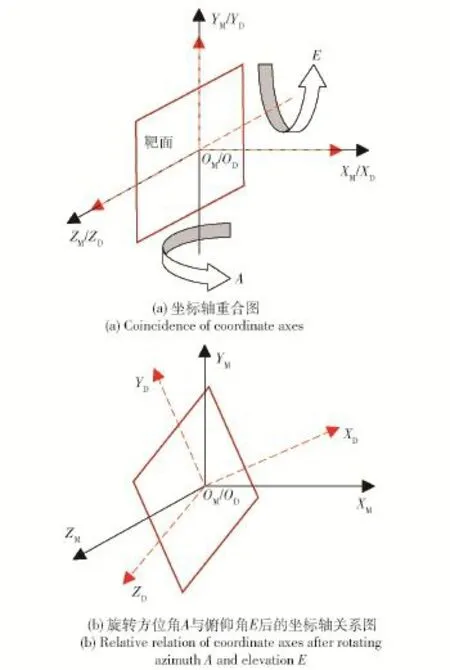
图2 雷达测量坐标系与指向坐标系Fig.2 Radar measurement coordinate system and direction coordinate system

图2中雷达绕YM轴旋转方位角A、绕ZD轴旋转俯仰角E后得到图2（b），靶面始终在YD轴和ZD轴构成的平面内。

雷达动态滞后即跟踪偏差一般均定义为雷达指向坐标系下的直接量测值，与光学测量像平面脱靶量偏差定义具有相同的物理意义。该坐标系的定义可给偏差修正带来很多方便。

2.2雷达动态滞后修正

因为重点讨论角度指向，不失一般性，距离以单位值代替。根据定向灵敏度事先标定结果以及直接测量值方位俯仰误差电压，方位俯仰动态滞后的角度量如（4）式所示。

由于无线电雷达动态滞后角度的物理意义与光学脱靶量一致。其中，tan（ΔAD）对应于ΔX/f，tan（ΔED）对应于ΔY/f，从而可获得空间目标在雷达指向坐标系下的归一化矢量为

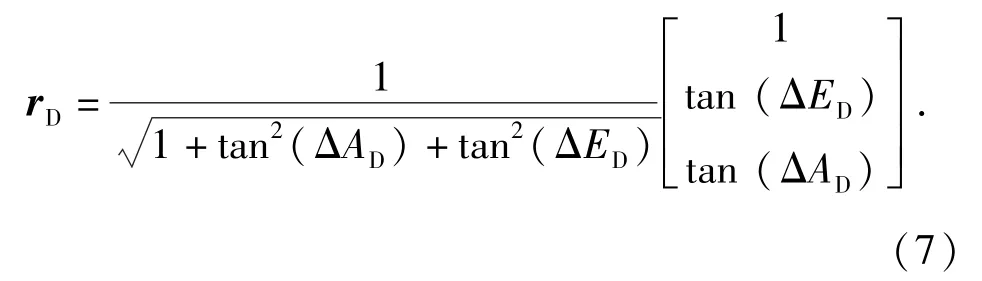
而雷达测量坐标系到指向坐标系的转换为先绕Y轴旋转方位角-A（旋转矩阵为RY（-A）），再绕Z轴旋转俯仰角E（旋转矩阵为RZ（E）），则总旋转矩阵为（A、E为编码器测量值）为

由（10）式可获得偏差修正后的目标方位、俯仰角的解析表达式（下标M表示测量坐标系，T表示真值）:

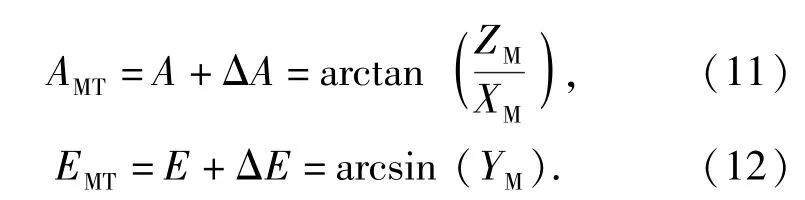
方位、俯仰角的具体值还需要视XM、YM、ZM的象限符号和角度的定义域而定。由于AMT是反正切函数，即使分母XM趋近于0，也不是数学上的奇异点，因为在自变量函数值ZM/XM趋近于无穷的过程中，将趋近于±π/2.

如果用于目标空间位置测量，（11）式和（12）式可直接应用，且可回避求解修正量的过程；如果用于跟踪，则需要求解方位、俯仰的修正量:

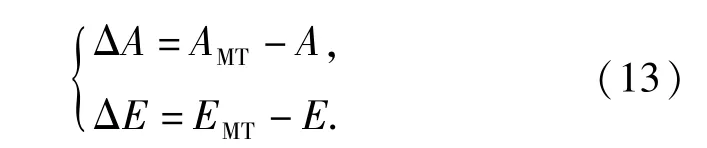
对于（10）式～（13）式，用ΔX/f代替tan（ΔAD），ΔY/f代替tan（ΔED），可获得光学脱靶量修正的新方法。

2.3电轴/光轴不垂直修正

关于电轴/光轴不垂直的修正，根据旋转角定义，相应旋转矩阵为

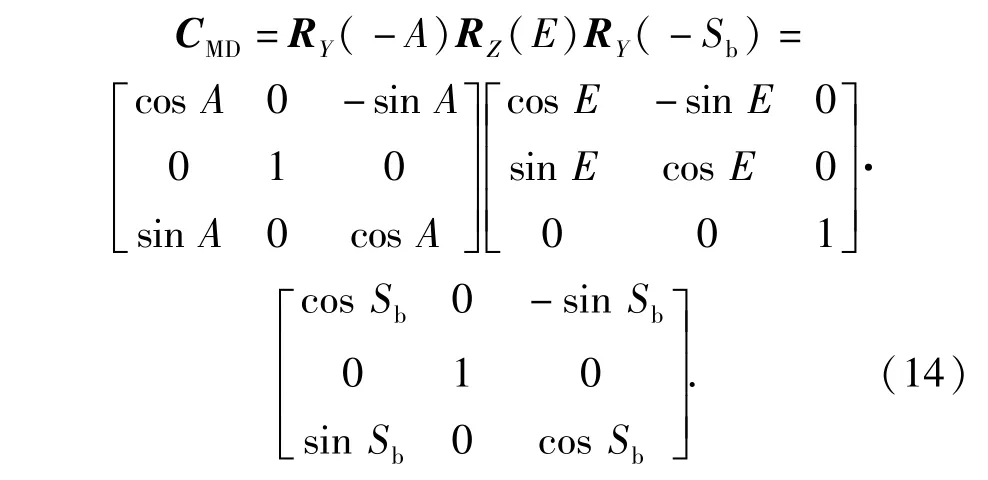
令rD=［1 0 0］T，即rM取旋转矩阵的第一列

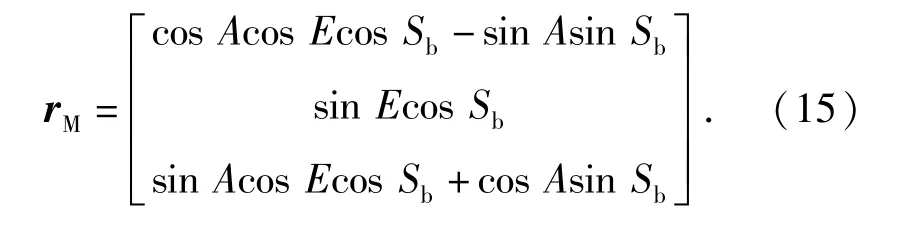
再利用（11）式～（13）式可以进行角度真值和修正量计算。

以上无论是雷达动态滞后修正，还是电轴/光轴不垂直修正，偏差无奇点修正方法是严格数学意义上的无误差修正方法，没有任何近似的假设。

3　等价性证明

3.1雷达动态滞后修正

利用三角函数关系可以证明关于雷达动态滞后修正（14）式与（1）式、（12）式与（2）式是等价的。

首先证明（12）式与（2）式即俯仰修正的等价性。将（9）式代入（12）式可得

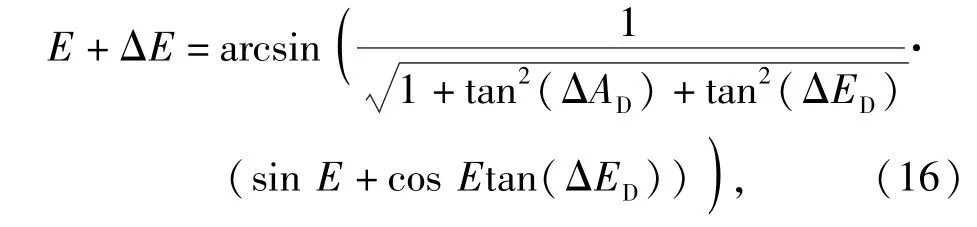
由于tan（ΔAD）与ΔX/f，tan（ΔED）与ΔY/f各自等价性，可以看出（12）式与（2）式是等价的。

下面证明（11）式与（1）式即方位修正的等价性。由（9）式和（11）式得

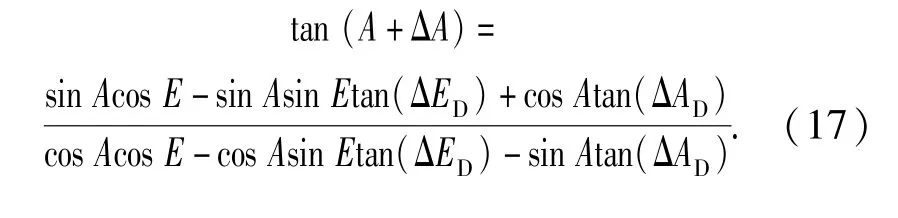
根据三角函数公式可得

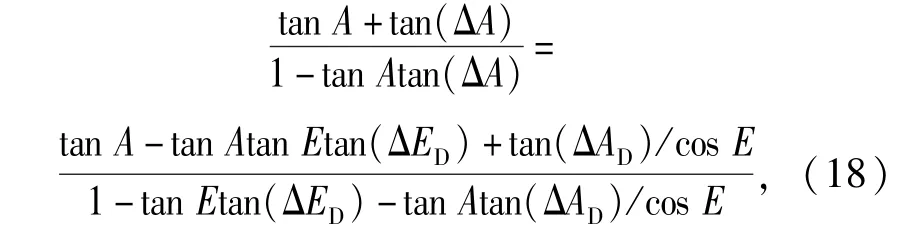
整理后可得

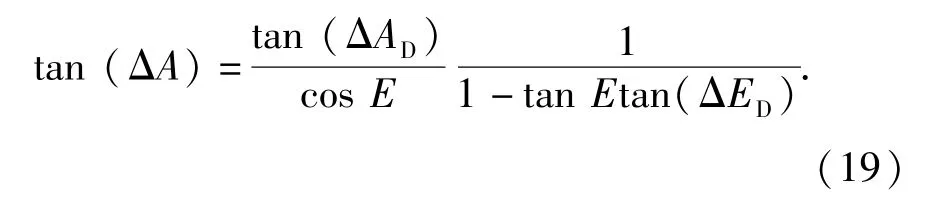
由于tan（ΔAD）与ΔX/f，tan（ΔED）与ΔY/f各自等价性，可以看出（19）式与（1）式是等价的，即（11）式与（1）式是等价的。

不难看出用ΔX/f代替tan（ΔAD），ΔY/f代替tan（ΔED），所获得的光学脱靶量修正方法与（1）式、（2）式也是等价的。

3.2电轴/光轴不垂直修正

关于电轴/光轴不垂直这里主要证明在不垂直量Sb是一个小量时本文计算与传统近似修正结果的一致性。

由于Sb是一个小量，有cos Sb≈1，sin Sb≈tan Sb≈Sb，同时将（15）式代入（11）式化简后可得

可以看出（20）式近似计算结果与传统的方位角修正量（6）式是等价的。

将（15）式代入（12）式直接可得

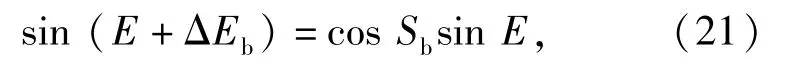
（21）式表明在不垂直量很小时，ΔEb≈0°，俯仰角可以不修正。

4　应用分析

从本文给出的无奇点修正结果看，无论是动态滞后还是其他轴系偏差引起的角度修正量均在±π/2或［0，π］范围内，不会出现无穷大的修正量。这符合天线运动的实际物理意义。

在无线电雷达或光学设备的高精度跟踪测量中，一般仰角高于75°时就不再做精度要求。主要是考虑到一方面高仰角稳定跟踪困难较大，另一方面即使能够跟踪，测量数据精度也较低。究其原因，主要是设备伺服系统有限的速度和加速度决定了其高仰角必定存在较明显的动态滞后，甚至无法跟踪的现象。这同时也是自跟踪系统驱动天线使跟踪误差无限接近零值的跟踪策略（简称为中心跟踪策略）必然带来的不可克服的问题。不同跟踪系统的差异主要在于可跟踪的高仰角门限不同，相同的是即使能够跟踪，仰角越高测角数据精度均越低。

表1给出了不同仰角下的5组典型偏差修正值，其中A=30°，方位、俯仰角偏差均为3 mrad；ΔAc、ΔEc分别为正割补偿法计算的方位、俯仰角修正量，ΔAm、ΔEm分别为无奇点修正法计算的方位、俯仰角修正量。

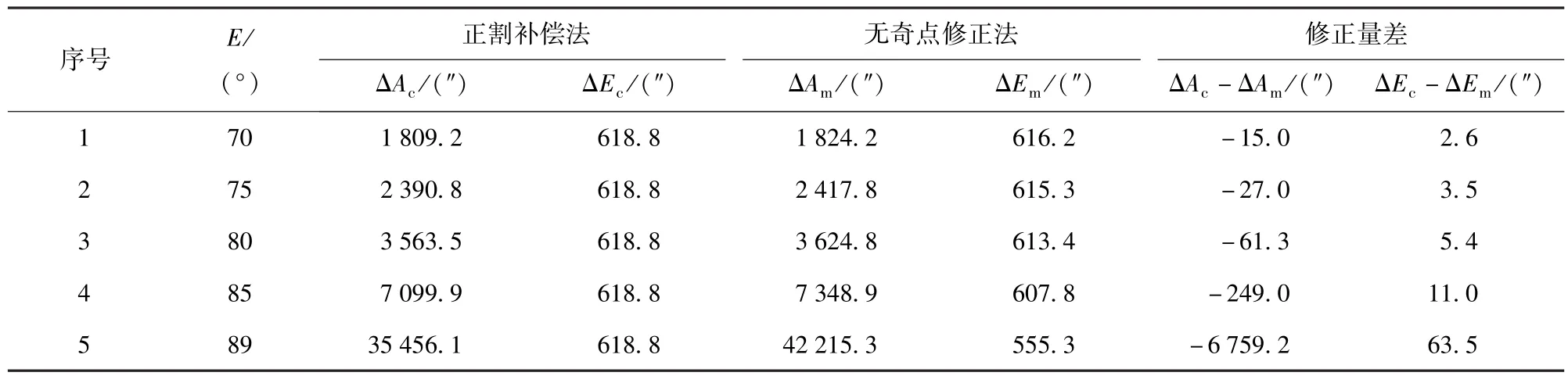
表1　通用正割补偿法与无奇点修正方法不同仰角典型结果比对（通用正割补偿法和无奇点修正方法计算的典型方位角和俯仰角偏差）Tab.1 Typical azimuth and elevation deviations calculated by the universal secant compensation method and the nonsingular modification method

从表1中可以看出，针对3 mrad的固定偏差，当仰角为89°，方位角修正偏差为6 759.2"，对于50ms的采样周期可造成37.6°/s的方位速度计算误差。该误差已经超出了多数雷达和光学设备的方位速度极限，从而造成了高仰角跟踪性能无法提高。

5　结论

本文基于指向坐标系的定义和坐标转换的原理，提出了无线电雷达和光学测量设备跟踪偏差和典型轴系误差的无奇点修正新方法，并证明了其有效性。不考虑计算截断误差，该方法能够实现无误差的修正，在高仰角时能够提高设备指向计算的精度，对于89°仰角、方位与俯仰角偏差均为3mrad情形，可改善正割补偿修正法指向计算存在的6 759.2"的方位角误差和63.5"的俯仰误差。

该方法理论上无近似假设，工程上使用方便，可用于提高方位-俯仰型测量设备高仰角跟踪性能、测量数据利用率和测量精度，缺点是仍不能完全克服高仰角盲区问题。

（References）

［1］ Samuel B，Robert P.Design and analysis of modern tracking systems［M］.Londo，UK:Artech House，1999:259-318.

［2］ 刘利生.外弹道测量数据处理［M］.北京:国防工业出版社，2002. LIU Li-sheng.Exterior ballistic measurement data processing［M］.Beijing:National Defense Industry Press，2002.（in Chinese）

［3］ 钟德安.航天测量船测控通信设备标校与校飞技术［M］.北京:国防工业出版社，2009. ZHONG De-an.Calibration and flight technology for measurement and communication equipment for space measurement ship［M］. Beijing:National Defense Industry Press，2009.（in Chinese）

［4］ 李淼.基于跟踪伺服系统仿真模型的光电经纬仪电视跟踪性能评价［D］.长春:中国科学院长春光学精密机械与物理研究所，2012. LI Miao.Tracking performance evaluation for electro-optic theodolite TV tracking based on servo system simulation model［D］. Changchun:Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，2012.（in Chinese）

［5］ Carlson D J，Looney C H.Coverage diagrams for x-y and elevation-over-azimuth antenna mounts，NASA-TN-D-2963［R］. Washington:Goddard Space Flight Center，1965.

［6］ Kurek N B.Secant correction for tracking pedestals［J］.IEEE Transactions on Automatic Control，1966，11（1）:135-136.

［7］ Senger S J.Device for secant correction of azimuth data in tracking radars:US，4032919［P］.1977-06-28.

［8］ Senger S J.Angle servo preamplifier.US，4178594［P］.1979-12-11.

［9］ Ji T B，Yang X H，Chen T，et al.Study on factors of influencing altitude-azimuth tracking performance near the zenith［J］.Journal of Optoelectronics Laser，2004，15（3）:283-286.

［10］ KhaliliM M，Hejazi F，Norouzi Y，et al.Secant method for bearing-only tracking problem［C］∥14th International Radar Symposium.Dresden，Germany:IEEE Computer Society，2013: 1-6.

［11］ 王红宣，吉桐伯，王伟国，等.地平式跟踪系统过顶问题研究［J］.吉林大学学报:信息科学版，2010，28（4）:347-351.WANG Hong-xuan，JI Tong-bo，WANG Wei-guo，et al.Solution to overcome zenith blind zone in altitude-azimuth optoelectronic system［J］.Journal of Jilin University:Information Science Edition，2010，28（4）:347-351.（in Chinese）

［12］ 董小萌，张平.两轴稳定平台的过顶盲区问题［J］.北京航空航天大学学报，2007，33（7）:811-815. DONG Xiao-meng，ZHANG Ping.Zenith blind zone of two-axis stabilized platform［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33（7）:811-815.（in Chinese）

［13］ 王锋，高亚飞，李清军.一种机载光电测量设备过顶跟踪技术［J］.现代电子技术，2012，35（17）:144-146. WANG Feng，GAO Ya-fei，LI Qing-jun.A vertex tracking technique for airborne photoelectric equipment［J］.Modern Electronics Technique，2012，35（17）:144-146.（in Chinese）

［14］ Zhai K，Yang D.Zenith pass problem of inter-satellite linkage antenna based on program guidance method［J］.Chinese Journal of Aeronautics，2008，21（1）:53-60.

［15］ Murakoshi T.Antenna stabilizing control system using a strapdown 2-axis azimuth/elevation method［J］.Microsystem Technologies，2005，11（8）:590-597.

［16］ Pankaj K G，Ramesh V，Bhatt K A，et al.Two-channel mono-pulse tracking receiver for onboard antenna tracking system［C］∥International Conference on Communication，Information＆amp;Computing Technology.Mumbai，India:IEEE Computer Society， 2012.

［17］ 吕韶昱，占荣辉，万建伟.雷达低空目标俯仰角测量提取的最大似然估计算法应用［J］.兵工学报，2008，29（9）:1059-1062. LYU Shao-yu，ZHAN Rong-hui，WAN Jian-wei.Maximum likelihood elevation extraction technique for radar low-altitude target［J］.Acta Armamentarii，2008，29（9）:1059-1062.（in Chinese）

［18］ 王文君，段晓君，朱炬波，等.某型弹载雷达测角系统误差模型辨识方法［J］.兵工学报，2014，35（2）:273-279. WANG Wen-jun，DUAN Xiao-jun，ZHU Ju-bo，et al.Identification method of systematic errors model of a missile-borne radar［J］.Acta Armamentarii，2014，35（2）:273-279.（in Chinese）

［19］ 黄师娟，张旭斌，董斌，等.雷达测量数据精度评估方法研究［J］.测试技术学报，2015，29（1）:36-40. HUANG Shi-juan，ZHANG Xu-bin，DONG Bin，et al.Research on accuracy evaluate method of radar testing data［J］.Journal of Test and Measurement Technology，2015，29（1）:36-40.（in Chinese）

［20］ Chen JH，Zhao W H，Liu B，et al.A new optics and radar strap-down measuring system［C］∥Proceeding of the International Astronautical Congress.Beijing:International Astronautical Federation，2013:8741-8748.

A Nonsingularity Modification Method of Angular Deviation in Azimuth-elevation Tracking Frame

CHEN Jia-hong，XIANG Jie，WANG Er-jian
（Joint Laboratory of Flight Vehicle Ocean-based Measurement and Control，Chinese Satellite Maritime Tracking and Controlling Department，Jiangyin 214431，Jiangsu，China）

The secant compensation method for correcting an angular deviation of radar tracking measurement system in azimuth-elevation polar coordinate frame is reviewed，and its pros and cons are analyzed. To overcome the complexity of derivation process and singularity，a tracking pointing coordinate system，i.e.，line-of-sight coordinate system，and a simple and practical nonsingularity compensation method based on coordinate transform principle are proposed.The equipollency between the proposed method and the universal secant compensation method based on solid geometry reasoning results is proven.The application of the proposed method in typical deviation correction of shafting and its effect on the tracking and measurement accuracies of radar system are also analyzed.For elevation angle of 89°，and azimuth and elevation angular deviations of 3 mrad，the azimuth error and elevation error calculated by the secant compensation method are 6 759.2"and 63.5"，respectively.The proposed method is benefit for the high precision tracking and measurement of space targets in the polar coordinate frame，especially to effectively improve the zenith tracking performance and the pointing accuracy with high elevation.

radar engineering；tracking and measurement；polar coordinate frame；deviation correction；secant compensation

V557+.5

A

1000-1093（2016）09-1708-07

10.3969/j.issn.1000-1093.2016.09.022

2016-02-02

国家自然科学基金项目（61403421）

陈嘉鸿（1971—），男，研究员。E-mail:stone_cjh@126.com