用跟踪微分器实现机器人自抗扰控制

李殿起，段勇

（1.沈阳工业大学机械工程学院，辽宁沈阳110870；2.沈阳工业大学信息科学与工程学院，辽宁沈阳110870）

用跟踪微分器实现机器人自抗扰控制

李殿起1，段勇2

（1.沈阳工业大学机械工程学院，辽宁沈阳110870；2.沈阳工业大学信息科学与工程学院，辽宁沈阳110870）

建立基于干扰估计的机器人非线性反馈控制系统并证明其稳定性，在此基础上提出一种适用于机器人跟踪控制的新型自抗扰控制器。该控制器不需实时计算复杂的机器人动态模型，由两个跟踪微分器（TD）构成：一个用于安排系统的过渡过程；另一个用来估计速度和加速度，TD的滤波特性使其对量测噪声具有抑制作用。由被控对象的控制量与所估计加速度的反馈构成的“扩张状态”来自动检测系统模型和外扰的实时作用并实时进行动态补偿。除了和以往的自抗扰控制器一样具有很好的适应能力和很强的鲁棒性外，它还具有需整定参数少的特点。仿真结果表明，该控制器是有效的且具有很强的鲁棒性，而且系统响应快且超调小。

控制科学与技术；机器人；自抗扰控制器；加速度估计；跟踪微分器；扩张状态

0　引言

机器人控制器设计按是否考虑动态模型可分为两类［1］。

一类是完全不考虑机器人的动态模型，只是按机器人实际轨迹与期望轨迹的偏差进行负反馈控制。这类控制器常采用PD或PID控制，它的主要优点是控制律简单，易于实现。但对于控制高速高精度的机器人来说，这类方法有两个明显的缺点:一是难于保证受控机器人具有良好的动态和静态品质；二是需要较大的控制能量。

另一类控制器设计方法是以模型为基础的控制方法，被称为动态控制。用动态控制方法设计的控制器可使被控机器人具有良好的动态和静态品质。然而由于各种动态控制方案中都无一例外地需要实时进行机器人动力学计算，而机器人又是一个复杂的多变量强耦合非线性系统，这就需要较大的在线计算量，给实时控制带来困难。

机器人动态控制的基本方案是计算力矩方法，也称为逆动力学算法。在此基础上又发展了机器人自适应控制、变结构控制和各种鲁棒控制设计方法等。上述方法要么依赖复杂的数学模型，要么设计方法复杂，实用性差。

在不计算复杂的机器人动态模型的前提下，如何实现机器人的高速高精度控制是一个值得研究的问题。而自抗扰控制器（ADRC）正是这样一种不依赖于系统模型的新型控制技术。

ADRC从其设计思想产生至今已经经历了20多年的曲折发展过程［2-4］，它的明确提出并形成完整的理论［5-6］仅仅发生在十几年前。目前，将其用于机器人控制的研究［7-9］较少，这些研究只是将ADRC原来的控制结构用在了机器人控制方面，没有针对机器人控制的特点有所改进。本文的目的就是根据ADRC的原理，设计一种适用于机器人控制的新型ADRC.

1　用干扰估计实现机器人单关节控制

机器人的动力学方程为

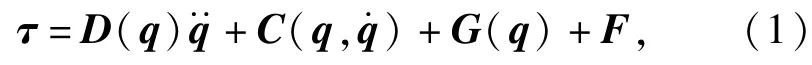
式中:子=［τ1，τ2，…，τn］T是加在各关节上的n×1广义力矩矢量，n是机器人的关节数；q=［q1，q2，…，qn］T是机器人的n×1关节矢量；D（q）是机器人的惯量矩阵，是n×n的实对称阵是n×1的非线性哥氏力和离心力矢量；G（q）为n×1重力矢量；F表示未建模动态和未知外扰作用。

将（1）式重写为

式中:M=diag［m11，m22，…，mnn］是n×n的实常量对角矩阵外，所有其他来自模型（已建模和未建模动态）和未知外扰的实时作用一并计入由（1）式和（2）式得

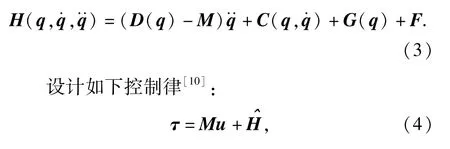
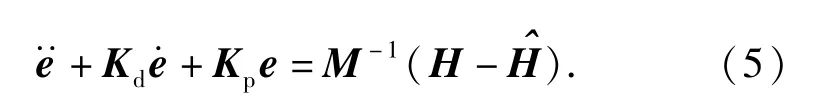
同时得到理想情况下的误差方程

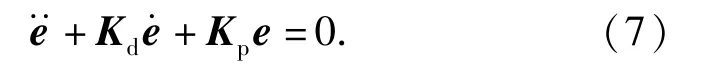
现在的关键问题是在不通过计算复杂动态模型（1）式的情况下，如何得到H的估计文献［11］提出用（8）式计算:

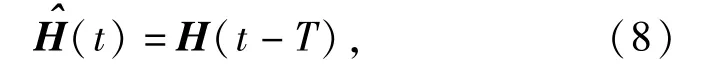
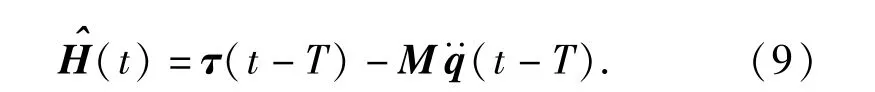
由（4）式得出如下控制律:

综上所述，（9）式能够实时估计所有来自模型和未知外扰的实时作用H，控制器（10）式使机器人动力学方程（1）式解耦和线性化，这样机器人多关节控制被转化为单关节控制。

2　非线性反馈控制系统的稳定性分析与证明

定义误差矢量

式中:ε（t）=［ε1（t），ε2（t），…，εn（t）］T。在控制律为（10）式的情况下，闭环系统的误差方程（5）式被重写为

ε（t）被认为是干扰输入，若ε（t）有界，则误差方程（12）式的解e（t）亦有界，这也是通常所说的有界输入、有界输出（BIBO）稳定性［10］。实际上，对于连续时间线性时不变系统，系统平衡状态的渐进稳定包含了系统的输入输出稳定。这也就是说，若ε（t）有界，且解耦的线性定常系统（7）式的平衡状态渐进稳定，则闭环系统（12）式是稳定的。用极点配置法，很容易保证系统（7）式的稳定性，目前的关键问题是如何保证ε（t）的有界性，文献［11］对此进行了分析，并得出如下结论:只要对角矩阵M的取值满足下面条件中的任意一个，即可保证ε（t）的有界性:

1）对角矩阵M=ηI，I是n×n的单位矩阵，η为一正常数值，同时需满足0＜η＜2ρ，其中ρ是惯量矩阵D（q）的特征值的下界。

2）如果惯量矩阵D（q）是对角阵，对角矩阵M=diag［η1，η2，…，ηn］，但需满足ηi＜2ρi，其中ρi为D（q）的对角元素的下界。

文献［12］对机器人的惯量矩阵的一致有界性进行了详细的分析，在不需推导D（q）的情况下，可方便地得到它的特征值下界。

ADRC一般采用非线性反馈控制，为此这里设计如下机器人非线性反馈控制律:

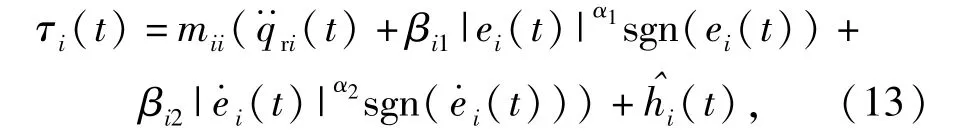
式中:βi1、βi2为增益系数；0＜αj＜1（j=1，2）时误差衰减速度最快，抑制扰动的能力最好［5］。若αj=1，（13）式变为（10）式，可见，机器人PD反馈控制是非线性反馈控制（13）式的特殊形式。

通过对角矩阵M的选取，保证了ε（t）的有界性。通过补偿项^H，把机器人非线性系统化为了线性系统。然而，在控制律为（13）式时，如何保证闭环系统的稳定性呢？下面给出证明。

由（2）式和（13）式两式得到闭环系统的误差方程为

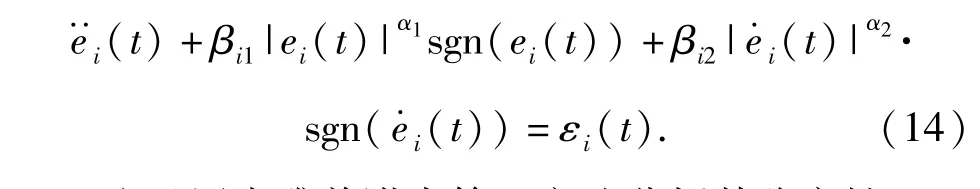
3　机器人自抗扰控制器

上述（9）式的控制思想与ADRC［6］自动检测扰动并进行实时补偿的方法是一致的。控制器（10）式在实施过程中，还存在着如下问题:首先时间延迟T在很小的情况下，估计值^H才能准确反映总干扰H，而且用（9）式计算^H时要用到加速度，众所周知，量测位移中不可避免地含有噪声，文献［11］用1阶微分求速度，2阶微分求取加速度的方法势必引起噪声的放大，采样时间T越小，噪声放大越严重［13］，为此这里提出用跟踪微分器（TD）跟踪位移和估计速度的同时一并估计出加速度的新方法。另外，控制器（10）式采用PD控制无法很好地解决系统快速性和超调之间的矛盾。出于以上两点考虑，将控制器（10）式改造成一种适用于机器人控制的ADRC.

在一般的控制系统中，比如上面的控制器（10）式采用PD控制，误差直接取成e=v-y，式中: v为设定值；y为系统输出。误差的这种取法就意味着让有一定惯性，不可能跳变的输出量y来跟踪可以跳变的量v，从而使初始误差很大，易引起“超调”，很不合理。加上这种线性组合方式不易解决快速性和超调的矛盾。因此，用TD和非线性控制来克服PD控制的缺点。

ADRC是由如下3部分组成:用一个TD来安排系统的过渡过程并提取其微分信号；用扩张状态观测器（ESO）来估计对象的状态变量和未知扰动的实时作用量并进行补偿；由安排的过渡过程与对象状态估计量之间误差的适当非线性组合和未知扰动估计量的补偿来生成控制信号。文献［14］介绍了ADRC设计的分离性原理，即按各自的工程意义分别独立地设计出以上3个组成部分，然后组合起来组成一个完整的ADRC.尽管目前还没能给出分离性原理的理论证明，但是大量仿真研究说明，对ADRC的设计完全可以使用这一分离性原理。

第2节证明了机器人非线性反馈控制系统的稳定性，在控制器（13）式的基础上设计的机器人ADRC如图1所示，图中所有变量的下标i表示机器人的关节号，以下叙述中i=1，2，…，n.图1中NLC表示非线性反馈控制，z-1表示时间延迟。与ADRC的3个组成部分相对应，机器人ADRC的组成分以下3个小节来介绍。

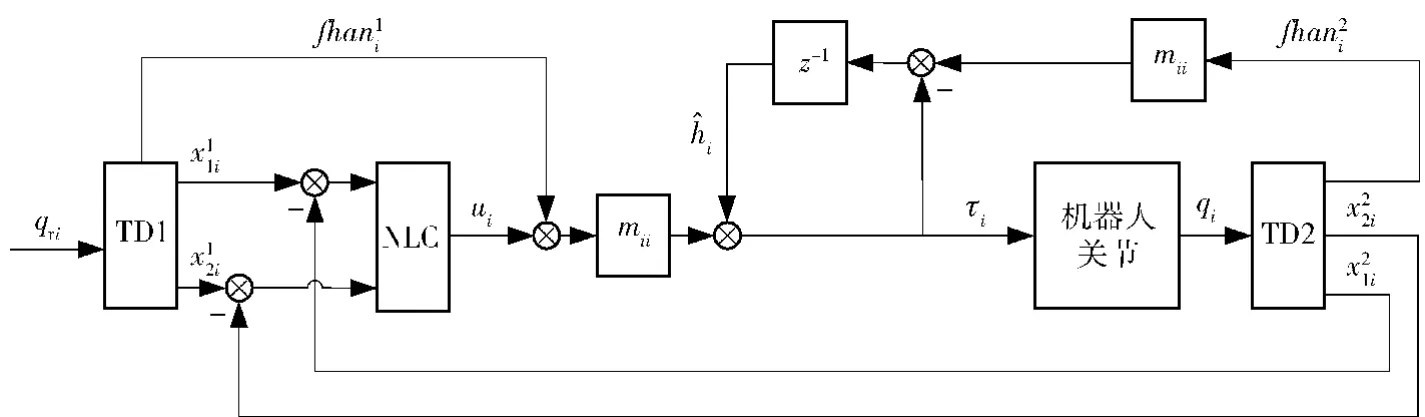
图1　机器人自抗扰控制结构图Fig.1 Structure drawing of active disturbance rejection controller for robot

3.1安排过渡过程

TD的离散形式为

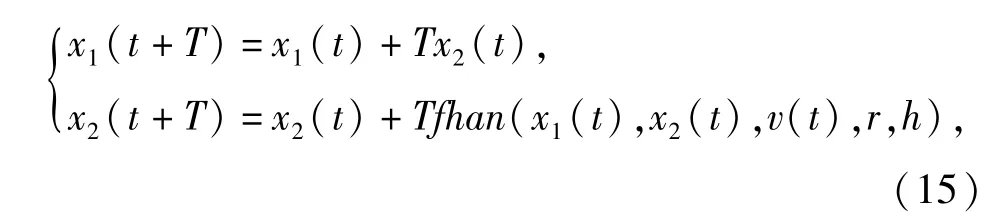
式中:T为采样周期；v（t）为输入信号；x1（t）跟踪v（t）；x2（t）为v（t）的微分；r为决定跟踪快慢的参数，称作速度因子；而h为输入信号被噪声污染时，决定滤波效果的参数，称作滤波因子；

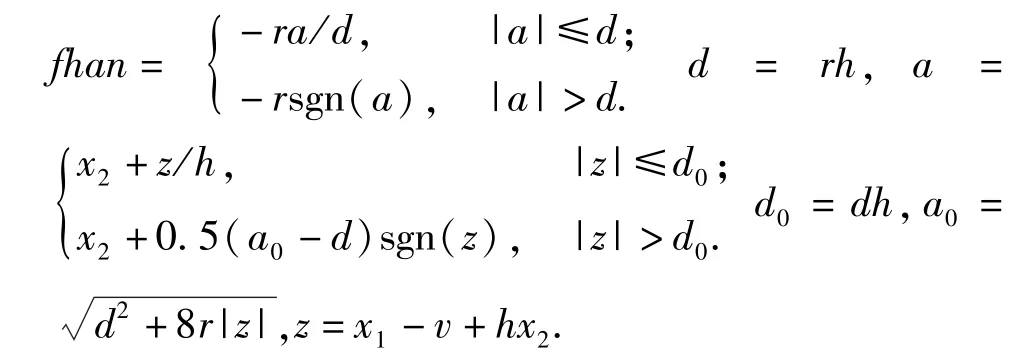
观察TD（15）式，若v（t）为输入位移，则x1（t）跟踪输入位移，x2（t）为速度，而x2（t+T）为其后一时刻的速度，根据速度和加速度的关系，显然（15）式中的fhan（x1（t），x2（t），v（t），r，h）就是加速度。

在图1中有两个TD（TD1和TD2）。为了区分TD1和TD2，给x1（t）、x2（t）、fhan加上标“1”、“2”，为了区分应用于不同的关节为其加下标“i”.

在这里使用离散TD有两个好处，能保证系统有较短的过渡过程而不出现超调，即使跟踪阶跃信号也没有超调［15］；在机器人控制过程中，轨迹规划的参考轨迹通常是不可微的，TD可以从不可微信号或含有噪声的信号中合理地提取连续可微的信号。因此，只要给定参考位移，即可由TD“自动规划”出参考速度和加速度。

3.2估计速度和加速度

如果将ADRC中的扩张状态观测器直接运用到机器人自抗扰控制中，由于每个ESO中有3个参数需要整定，对于具有n个自由度的机器人来说，仅ESO部分就有3n个参数需要整定，其难度是可想而知的。为此这里提出用TD估计速度和加速度。

如图1所示，当TD2的输入为机器人关节角位移qi的量测值时，x21i（t）跟踪机器人关节的实际转见，在这里TD2实际上是一个速度、加速度估计器。为了尽可能好地提取出速度和加速度信号，通常速度因子r2取得大些。因为TD具有类似于线性低通滤波器的频率特性［15］，所以用它来跟踪机器人关节的输出qi具有较好的噪声抑制作用。一般系统的输出均含有一定噪声，因此滤波因子h2取适当大些的值。

3.3非线性反馈控制律

控制律（13）式中的非线性PD反馈为

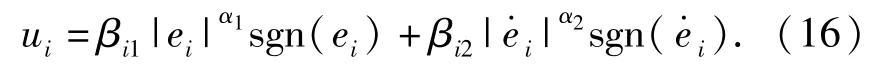
当0＜αj＜1（j=1，2）时确定的误差反馈律（16）式具有小误差、大增益，大误差、小增益的特点。

文献［16］已经证明了非线性TD的收敛性，另外，TD的速度因子r越大，对位置和速度跟踪得越快，就能越快地达到设定值。因此，当机器人非线性反馈控制律（13）式用在如图1所示的机器人ADRC中时，机器人关节的位置误差和速度误差为ei=

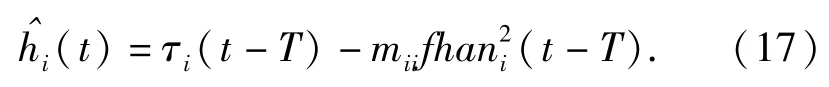
从图1可见本文的机器人ADRC与文献［6］提出的ADRC的一般形式是不同的。在上述机器人控制器（13）式里“未知扰动”是由（17）式来确定的，它是由被控对象的控制量τi（t-T）与所估计加速度的反馈构成的。按着ESO的定义，为与其“扩张状态”相对应，此处把称作“扩张状态”。用（17）式来检测扰动，有两点好处:1）和以往ADRC中的ESO相比，需要整定的参数很少；2）加速度是力最直接的反映，用它来检测扰动物理意义更加明确。

所谓“自抗扰”就在于补偿项^hi（t），系统的“未建模动态”和“未知外扰”的实时作用一并给予估计和补偿，把非线性系统化为线性系统。当机器人的负载发生变化时，这种控制器具有很好的适应能力和很强的鲁棒性。

4　仿真验证与对比分析

下面以文献［17］中的一个3自由度直接驱动机器人为例进行仿真研究，该机器人的3个关节均为旋转关节，能进行高速运动。仿真中需要的机器人动态模型及相关参数请参见文献［17］。

4.1仿真参数设置

在仿真或实际控制中，将TD（15）式写成固定的功能模块，如图1所示，控制每个关节时直接进行函数调用，非常方便。

仿真中为了模拟量测噪声，在图1所示的机器人的每个关节位移输出qi（i=1，2，3）中加入零均值高斯白噪声，若量测装置为脉冲编码器，设其分辨率为θm，则白噪声的方差为，这里的直接驱动机器人采用2 000 p/r的脉冲编码器。

mii的取值很重要，它关系到机器人控制的稳定性，因这里是直接驱动机器人，可按第2节中关于M取值方法中的第二个结论来取值，事实上，转动惯量大的关节所使用电机的转动惯量也大，这样此处mii分别取关节电机转动惯量Ji的10倍左右，个别做适当调整。即mii（i=1，2，3）分别为0.028 kg·m2、0.028 kg·m2和0.002 5 kg·m2.

βi1、βi2的取值通常根据系统时间尺度整定［18］。在这里为了具有可比性，控制器（13）式的增益βi1、βi2可取为PD控制中的kpi、kdi，对误差方程（7）式采用极点配置法得到PD控制中的kpi、kdi，此时βi1、βi2的取值分别为:β11=β21=β31=30，β12=β22=β32=12.

其他参数取值都比较容易，满足前面小节中所述条件要求即可。在这里根据噪声抑制和跟踪速度情况，TD1中h1=0.01，r1为20～400；TD2中h2= 0.02，r2为80～800.非线性反馈控制律（13）式中α1=0.8，α2=0.5；采样时间T=0.005 s，仿真时间为8 s.

4.2自抗扰控制仿真结果

4.2.1系统的阶跃响应

为了验证控制器（13）式的有效性，在图1所示的控制系统中，为qri（i=1，2，3）分别设置单位阶跃输入，取r1=30，r2=80，其他值如上所述，得到该系统的阶跃时间响应如图2所示。从仿真中可以得出，3个关节的位移响应最大超调量均不到3％.实际上，r1和r2取上述范围内的任意组合，只要r2比r1大几倍，就能使3个关节的位移响应最大超调量都不超过6％.当然，通过调整参数也可以使系统的阶跃时间响应无超调，这表明了采用TD1安排系统过渡过程的合理性。

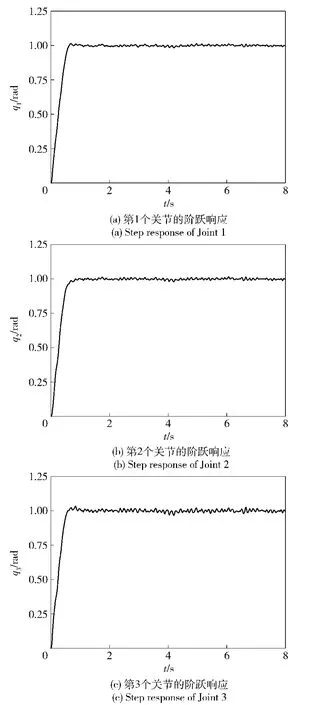
图2　3个关节的阶跃响应Fig.2 Step responses of 3 joints

4.2.2轨迹跟踪

根据实际情况，直接驱动机器人的3个关节均在一定转角范围内连续周期性地进行正、反向运动，在每个循环内机器人关节跟踪下面的参考轨迹［19］:

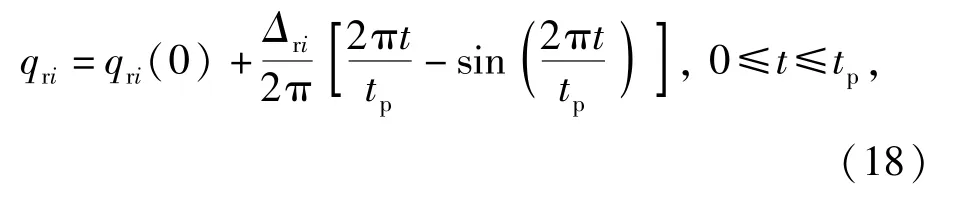
式中:Δri=qri（tp）-qri（0），i=1，2，3，且tp是一个循环的终止时间，qri（0）是起始关节角度，qri（tp）是终止关节角度。（18）式所表示的参考轨迹充分考虑到了机器人的加减速状态［20］，表示实际中较不利的输入情况。

（18）式中的tp取不同的值，就得到不同振幅和频率的参考轨迹。限于篇幅，仿真中tp=1.6 s，即要求机器人每个关节在1.6 s内从起始关节角度qri（0）运动到终止关节角度qri（tp），用（qri（0），表示。3个关节的起始和终止角度分别为

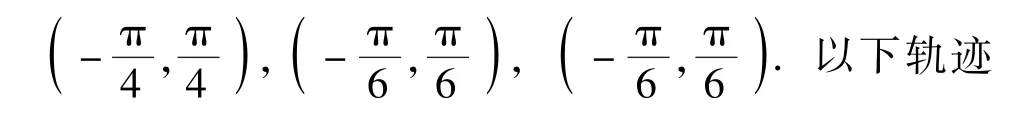
跟踪过程中均给出8 s内5个周期的仿真结果。

图3为轨迹跟踪结果，e1、e2、e3分别为机器人各个关节的轨迹跟踪误差，从图3可见跟踪误差较小，各关节相对于参考轨迹来说，跟踪偏差的相对值不超过3％.注意这是在具有量测噪声情况下的跟踪误差，若在没有量测噪声的情况下，跟踪误差是很小的。当然，改变上述仿真参数设置，可进一步提高跟踪精度。

从图2和图3可以看出，第3个关节与其他两个关节相比，跟踪效果相对较差，为了清楚起见，下面只给出第3个关节的仿真结果。另外，需要说明的是以下各图中虚线为由（18）式描述的期望轨迹，实线为跟踪轨迹。

4.2.3鲁棒性验证

为了验证控制器的鲁棒性，保持上面的所有参数不变，在机器人运动开始2 s后，在机器人每个关节上加上阶跃负载τdi:

式中:τdmaxi为上述机器人关节电机的最大峰值堵转扭矩，为机器人手部承受负载达到最不利情况时，电机能够承受的力矩，其中τdmax1=0.84 N·m，τdmax2= 6.66 N·m，τdmax3=6.66 N·m.

仿真结果发现，第1和第2个关节的轨迹跟踪情况变化不大，只有第3个关节变化稍大（如图4所示）。如果用e3L表示第3个关节加上阶跃负载τdi后的跟踪误差，e3为未加τdi前的跟踪误差，二者之间的差值即跟踪误差的变化可以用来衡量控制器的鲁棒性:Δe=e3-e3L.

图3 3个关节的轨迹跟踪误差Fig.3 Tracking errors of 3 joints

图5是Δe随仿真时间变化的曲线，从图5可见加上阶跃负载τdi前后，跟踪误差变化Δe的最大值为0.15 rad，发生在加上或去掉τdi的瞬时，Δe从整个时间历程来说较小。这说明控制器具有很强的鲁棒性。

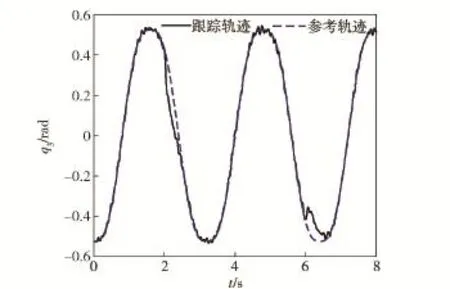
图4　加上阶跃负载后第3个关节的轨迹跟踪Fig.4 Trajectory tracking of Joint3 under step load

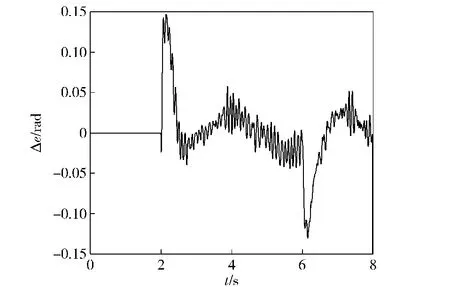
图5　Δe随时间变化的曲线Fig.5 Time domain diagram ofΔe

4.3对比分析

为了进一步说明机器人ADRC（13）式的有效性和合理性，将其与控制器（10）式进行对比分析。

4.3.1跟踪效果对比

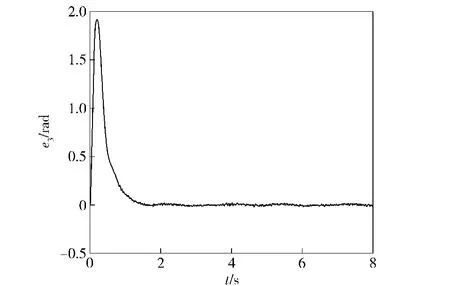
图6　第3个关节的轨迹跟踪误差（控制器为（10）式）Fig.6 Tracking errors of Joint3（controller is Eq.（10））

为了具有可比性，在（10）式中令位置增益kpi= βi1，速度增益kdi=βi2，其他参数亦不变。图6为第3个关节的轨迹跟踪结果，从图6可见，跟踪初始阶段产生了很大误差，调整增益，也没有明显改善。而当采用机器人ADRC（13）式时，自始至终的跟踪误差都不大（见图3），这说明系统响应具有快速性，能够解决快速性和超调之间的矛盾，这进一步说明了采用TD1安排系统过渡过程的合理性。

4.3.2对噪声敏感程度对比

为了比较两种控制器对噪声的敏感程度，只改变量测白噪声方差的取值，而保持上面的所有其他参数不变。前面白噪声方差取值当放大到2.1R时，控制器（10）式由于噪声的影响而失稳。然而，对于机器人ADRC（13）式，即使噪声放大到10R甚至更高仍能进行有效的轨迹跟踪，图7为噪声放大10倍时第3个关节的轨迹跟踪结果。这充分说明了用TD2作为滤波估计器估计速度和加速度的合理性。

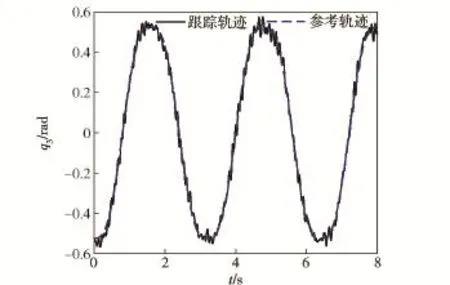
图7　第3个关节的轨迹跟踪（控制器为（13）式）Fig.7 Trajectory tracking of Joint3（controller is Eq.（13））

5　结论

本文提出了用TD跟踪位移和估计速度的同时一并估计出加速度的新方法，拓展了TD的应用范围。由被控对象的控制量与所估计加速度的反馈构成的“扩张状态”实际上已使系统实现动态补偿线性化，故无需建立并实时计算复杂的机器人模型，仅需知道机器人惯量矩阵的下界即可。由两个TD构成的ADRC是针对非线性、强耦合的机器人系统而设计的，它在控制过程中只需给定期望位置。仿真与对比分析结果表明:用TD1安排系统的过渡过程使系统响应快且超调小；用TD2作为滤波估计器估计速度和加速度使这种控制器对量测噪声具有很好的抑制作用；机器人在高速运动时，该控制器亦能实现较精确的跟踪控制。这种ADRC也可用于其他运动控制当中。

（References）

［1］ 霍伟.机器人动力学与控制［M］.北京:高等教育出版社，2005:123-140. HUOWei.Robot dynamics and control［M］.Beijing:Higher Education Press，2005:123-140.（in Chinese）

［2］ 黄一，张文革.自抗扰控制器的发展［J］.控制理论与应用，2002，19（4）:485-492. HUANG Yi，ZHANG Wen-ge.Development of active disturbance rejection controller［J］.Control Theory＆amp;Applications，2002，19（4）:485-492.（in Chinese）

［3］ 高志强.自抗扰控制思想探究［J］.控制理论与应用，2013，30（12）:1498-1510. GAO Zhi-qiang.On the foundation of active disturbance rejection control［J］.Control Theory＆amp;Applications，2013，30（12）: 1498-1510.（in Chinese）

［4］ 夏元清，付梦印，邓志红，等.滑模控制和自抗扰控制的研究进展［J］.控制理论与应用，2013，30（2）:137-147. XIA Yuan-qing，FU Meng-yin，DENG Zhi-hong，et al.Recent developments in sliding mode control and active disturbance rejection control［J］.Control Theory＆amp;Applications，2013，30（2）: 137-147.（in Chinese）

［5］ 韩京清.控制系统的非光滑综合［C］∥第十九届中国控制会议论文集（二）.香港:中国自动化学会控制理论专业委员会，2000:483-488. HAN Jing-qing.Non-smooth feedback synthesis for control system［C］∥Proceedings of 19th Chinese Conference on Control.Hong Kong，China:Technical Committee on Control Theory，Chinese Association of Automation，2000:483-488.（in Chinese）

［6］ 韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13（1）:19-23. HAN Jing-qing.Auto-disturbances-rejection controller and its applications［J］.Control and Decision，1998，13（1）:19-23.（in Chinese）

［7］ Huang Y，Luo Z W，Svinin M，et al.Extended state observer based technique for control of robot systems［C］∥4th World Congress on Intelligent Control and Automation.Shanghai，China:Institute of Electrical and Electronics Engineers Inc，2002:2807-2811.

［8］ Su Y X，Duan B Y，Zheng C H，et al.Disturbance-rejection high-precision motion control of aStewart platform［J］.IEEE Transactions on Control Systems Technology，2004，12（3）:364-374.

［9］ 阮晓钢，王旭，陈志刚.独轮机器人的建模与自抗扰控制算法［J］.控制与决策，2015，30（12）:2253-2258. RUAN Xiao-gang，WANG Xu，CHEN Zhi-gang.Modeling and active disturbance rejection control algorithm of single wheel robot［J］.Control and Decision，2015，30（12）:2253-2258.（inChinese）

［10］ 熊有伦，丁汉，刘恩沧.机器人学［M］.北京:机械工业出版社，1993:200-219. XIONG You-lun，DING Han，LIU En-cang.Robotics［M］.Beijing:China Machine Press，1993:200-219.（in Chinese）

［11］ Hsia T C，Gao L S.Robot manipulator control using decentralized linear time-invariant time-delayed joint controllers［C］∥1990 IEEE International Conference on Robotics and Automation.Cincinnati，OH，US:IEEE，1990:2070-2075.

［12］ Ghorbel F，Srinivasan B，Spong MW.On the uniform boundedness of the inertia matrix of serial robot manipulators［J］.Journal of Robotic Systems，1998，15（1）:17-28.

［13］ Belanger PR，Dobrovolny P，Helmy A，et al.Estimation of angular velocity and acceleration from shaft-encoder measurements［J］.International Journal of Robotics Research，1998，17（11）:1225-1233.

［14］ 黄焕袍，武利强，韩京清，等.火电单元机组协调系统的自抗扰控制方案研究［J］.中国电机工程学报，2004，24（10）: 168-173. HUANG Huan-pao，WU Li-qiang，HAN Jing-qing，et al.A study of active disturbance rejection control on unit coordinated control system in thermal power plant［J］.Proceedings of the Chinese Society for Electrical Engineering，2004，24（10）:168-173.（in Chinese）

［15］ 韩京清，黄远灿.二阶跟踪—微分器的频率特性［J］.数学的实践与认识，2003，33（3）:71-74. HAN Jing-qing，HUANG Yuan-can.Frequency characteristic of second-order tracking-differentiator［J］.Mathematics in Practice and Theory，2003，33（3）:71-74.（in Chinese）

［16］ Guo B Z，Zhao ZL.on convergence of racking differentiator［J］. International Journal of Control，2011，84（4）:693-701.

［17］ Li D Q，Xue D Y，Li T，et al.Dynamic model of a 3 DOF direct drive robot and its control mode［C］∥IEEE International Conference on Control and Automation.Guangzhou，China:IEEE Control Systems Society，2007:2694-2698.

［18］ 李述清，张胜修，刘毅男，等.根据系统时间尺度整定自抗扰控制器参数［J］.控制理论与应用，2012，29（1）:125-129. LI Shu-qing，ZHANG Sheng-xiu，LIU Yi-nan，et al.Parametertuning in active disturbance rejection controller using time scale［J］.Control Theory＆amp;Applications，2012，29（1）:125-129.（in Chinese）

［19］ Kane T R，Levinson D A.The use of Kane's dynamical equations in robotics［J］.International Journal of Robotics Research，1983，2（3）:3-21.

［20］ 李殿起，薛定宇，崔建国，等.一种新型的速度和加速度估计器［J］.系统仿真学报.2008，20（15）:4132-4135. LI Dian-qi，XUE Ding-yu，CUI Jian-guo，et al.Novel velocity and acceleration estimator［J］.Journal of System Simulation，2008，20（15）:4132-4135.（in Chinese）

Implementation of Active Disturbance Rejection Control of Robot by Tracking Differentiator

LI Dian-qi1，DUAN Yong2
（1.School of Mechanical Engineering，Shenyang University of Technology，Shenyang 110870，Liaoning，China；2.School of Information Science and Engineering，Shenyang University of Technology，Shenyang 110870，Liaoning，China）

A disturbance estimation-based nonlinear feedback control system for robots is presented，and its stability is demonstrated.On the basis of result，a novel active disturbance rejection controller（ARDC）is proposed，which avoids the burdensome online computation of robot inverse dynamics and implement the trajectory tracking of robots.The controller comprises two tracking differentiators（TDs），one is used to arrange the transient process of system，and the other is used to estimate velocity and acceleration.TD can attenuate measurement noise due to its filtering characteristic.“Extended state”，comprising the control input of controlled object and the feedback of estimated acceleration，is used to detect the real time effects of system model and the external disturbances，and then dynamically compensate their real-time effects.The proposed ARDC has the same good adaptability and expected robustness as previous ADRC，and it also has the characteristic of less parameters adjustment.Numerical results show that the control system has less overshoot，rapid response，and robustness.

control science and technology；robot；active disturbance rejection controller；acceleration estimation；tracking differentiator；extended state

TP24

A

1000-1093（2016）09-1721-09

10.3969/j.issn.1000-1093.2016.09.024

2015-12-24

国家自然科学基金项目（60905054）；辽宁省高等学校优秀科技人才支持计划项目（LR2015045）；辽宁省自然科学基金项目（2015020010）

李殿起（1968—），男，副教授。E-mail:dianqi@126.com