空间大型末端执行器柔性绳索捕获动力学研究

荣吉利，辛鹏飞，诸葛迅，杨永泰，项大林

（1.北京理工大学宇航学院力学系，北京100081；2.北京航天动力研究所，北京100076；3.中国科学院泉州装备制造研究所，福建泉州362000）

空间大型末端执行器柔性绳索捕获动力学研究

荣吉利1，辛鹏飞1，诸葛迅2，杨永泰3，项大林1

（1.北京理工大学宇航学院力学系，北京100081；2.北京航天动力研究所，北京100076；3.中国科学院泉州装备制造研究所，福建泉州362000）

针对绳索式末端执行器缠绕及捕获卫星过程中的动力学问题，采用绝对节点坐标方法描述横观各向同性柔性绳索的缠绕运动，及卡尔丹角描述刚体卫星的姿态运动，并引入绳索与目标间的非线性动力学模型，建立包含末端执行器固定环和旋转环、绳索及被捕获卫星抓杆在内的刚柔耦合动力学模型。结合广义α法以及工程上常用的Scaling技术，利用Matlab开发了计算程序，实现动力学方程的高效精确数值求解。计算结果表明：此模型能较好地模拟柔性绳索缠绕及捕获卫星的过程，同时给出捕获过程中卫星姿态的变化及绳索的运动和受力情况，为实际工程中捕获机构的设计和试验提供一定的参考依据。

航空、航天科学技术基础学科；捕获动力学；柔性绳索；卫星姿态；刚柔耦合；绝对节点坐标方法

0　引言

随着航天技术的发展，在轨服务技术已成为航天高科技领域的一个研究热点，而机械臂末端执行器对目标载荷的成功捕获是其中的关键，也是我国载人航天三期工程正在大力发展的内容之一。这一技术的研究，直接影响着我国空间站的长期工作性能以及往返运送货物和宇航员的成本、安全问题，对于我国力求在2020年前后建成大型空间站的目标具有重大现实意义。

基于轻质原则，捕获机构可采用国际空间站上使用的柔性绳索缠绕捕获技术［1-3］。图1为空间机械臂捕获卫星简易示意图。对于绳索式末端执行器捕获动力学的研究难点主要有两方面:一是微重力环境下具有大柔性、大变形特性的绳索建模困难；二是捕获过程中复杂的非线性接触碰撞力较难描述。

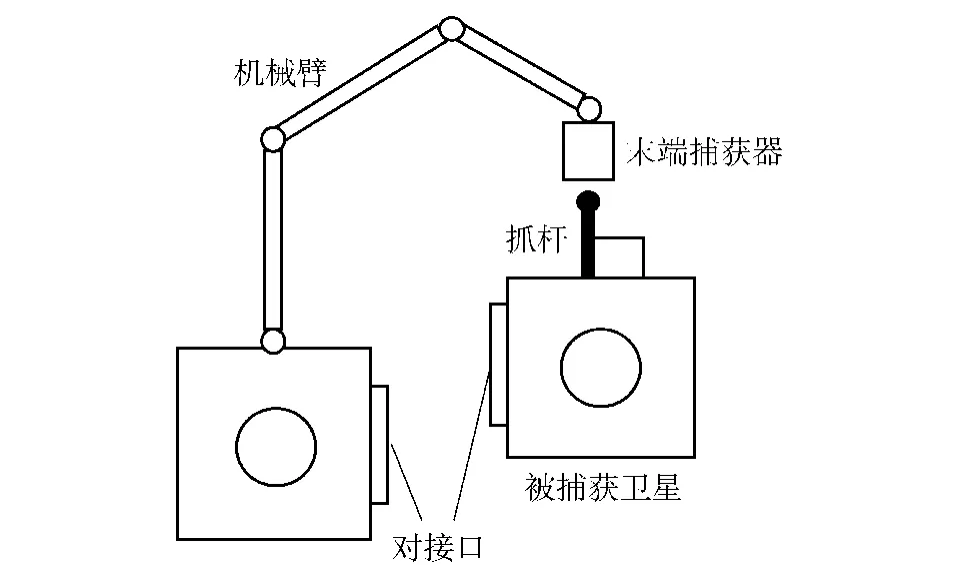
图1　空间机械臂捕获卫星示意图Fig.1 Schematic diagram of a space manipulator capturing a satellite

柔性绳索的动力学特性研究由来已久。与重力环境下工程设施中的索缆不同，空间绳索在运动过程中，当内部张力很小时，容易出现应力松弛等力学特性，增加了动力学建模的困难。于洋等［4］分类介绍了国内外几种常用的空间绳索系统动力学建模方法:离散刚体模型、弹性体模型、离散质点模型等，分别适用于特定工况下的绳索特性研究。国内学者如陈钦等［5］采用集中参数法建立了空间绳网系统刚柔耦合动力学模型，研究了其发射展开的动力学问题；针对绳索类捕获机构，谭益松等［6］采用离散控制模型对柔性绳索进行了建模，分析了柔性绳索在捕获过程中的复杂动力学问题。但两种方法均不能精确得到绳索的位形和受力状况，约束关系的表现形式也极其复杂。因此考虑空间柔性绳索做复杂运动时，需要新的绳索动力学建模方法。

Shabana等［7］基于有限元和连续介质力学理论，首次提出绝对节点坐标方法（ANCF），采用节点坐标、节点坐标物质导数作为广义坐标，可以真实反映大变形柔性体的动力学行为。杨永泰等［8］基于此方法，建立了末端带集中质量的空间双连杆柔性机械臂的刚柔耦合动力学模型，研究了机械臂的空间运动规划及柔性变形问题。朱大鹏［9］采用该方法建立动力学模型，采用工程正应变与剪应变描述梁单元的变形，进而将考虑截面扭转变形的缩减直梁单元推广为曲梁单元。魏承等［10-11］采用缩减的绳索单元对末端执行器绳索捕获过程中的接触力进行了研究。潘冬等［12］采用实验研究的方法分析了缠绕过程的接触力问题，但理论仿真所采用的绳索单元均未对横观各向同性材料进行相应的处理。

本文提出基于ANCF描述的绳索单元，推导了其单元应变能及质量矩阵的形式，用于描述空间机械臂末端捕获机构中柔性绳索的运动，用卡尔丹角描述被捕获卫星的空间姿态运动，建立了以旋转环的转动带动绳索运动，继而使被捕获卫星到达目标方位的刚柔耦合动力学模型。结合广义α法［13］以及工程上常用的Scaling技术［14］，开发了计算程序，实现了动力学方程的高效精确数值求解。计算结果表明，建立的柔性绳索动力学模型能够较好地模拟机械臂末端执行器绳索式捕获机构的缠绕及捕获过程。

1　基于ANCF描述的柔性绳索单元

在Gerstmayr等［15］直梁单元研究的基础上，基于Euler-Bernoulli梁假设，刘铖［16］提出了ANCF缩减三维曲梁单元。在此框架基础上，本文提出ANCF缩减三维绳索单元，且根据实际情况，将绳索视为横观各向同性材料。图2为三维绳索单元变形示意图。

该绳索单元初始长度为l，具有2个节点，每个节点有6个绝对坐标，从而有如下12个绝对节点坐标组成的列向量:

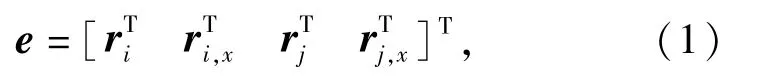
式中:ri，x为节点i的位置矢量ri对ξ方向的偏导数矢量，即ri，x=∂ri/∂x，该矢量用来描述绳索单元中线的变形。绳索单元中线上任一点P的位置矢量可通过单元广义坐标与单元形函数表示为

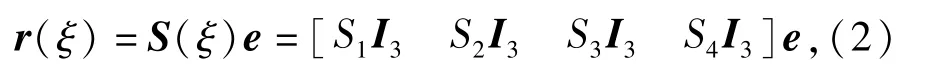
式中:I3为3×3的单位矩阵；ξ为P点在单元坐标系oξyz中的坐标；S为绳索单元的形函数，其分量表达式为S1=1-3ξ2+2ξ3，S2=l（ξ-2ξ2+ξ3），S3= 3ξ2-2ξ3，S4=l（-ξ2+ξ3），ξ=x/l.

弧长坐标为

图2　三维绳索单元变形描述示意图Fig.2 Deformation of 3D flexible rope element

由于在末端执行器工作中，绳索的弯曲刚度对当前系统的动力学特性影响很小，故在动力学建模中可以忽略，计算轴向应变时只计拉伸应变而忽略弯曲应变。在初始构型中，设r0为P点所在截面与中线交点的位置矢量，P点附近沿着中线方向的微元长度的平方可表示为

在当前构型中，该微元变为d sP，设r为P点所在截面与中线交点的位置矢量，其长度的平方同样可表示为

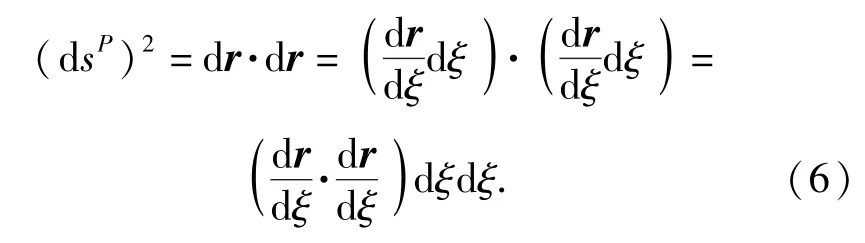
根据Green-Lagrange应变张量的定义，在P点附近微元长度的变化与Green-Lagrange轴向应变关系为

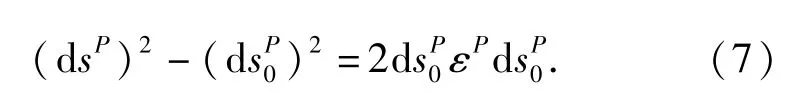
将（5）式、（6）式代入（7）式，并结合（4）式，可得该点的Green-Lagrange轴向应变为

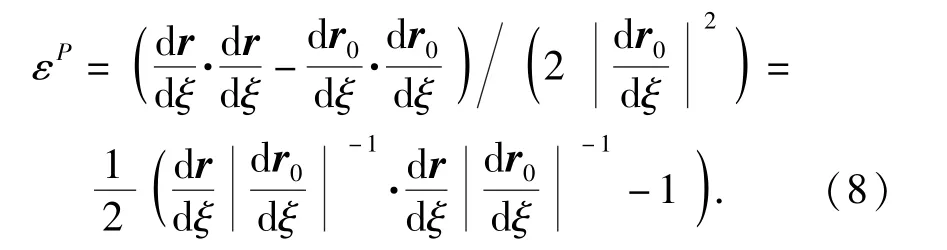
由于绳索为横观各向同性材料，根据复合材料力学知识可知

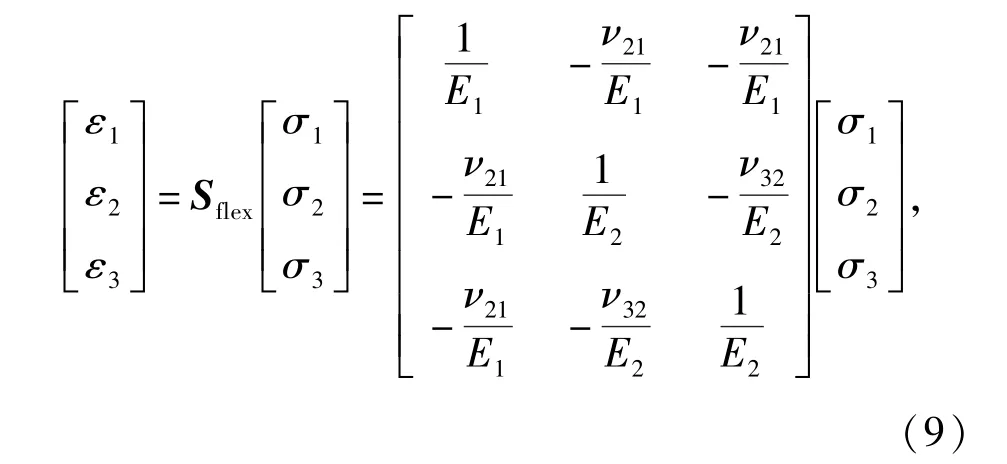
式中:ε1和σ1为绳索的轴向应变和应力；ε2和ε3为绳索的两个横向应变，σ2和σ3为对应的两个横向应力；Sflex表示绳索单元的柔度矩阵；E1为轴向弹性模量；E2为横向弹性模量；v21为轴向与横向之间泊松比；v32为横向与横向之间泊松比。

由（9）式可得P点的轴向应力为

由绳索的横观各向同性以及只受拉不受弯的特性得

将（11）式代入（10）式可得

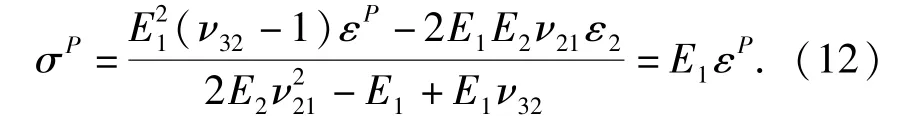
在得到绳索单元上任一点的轴向应变和轴向应力后，通过对该单元初始构型的体积分，单元应变能可表示为

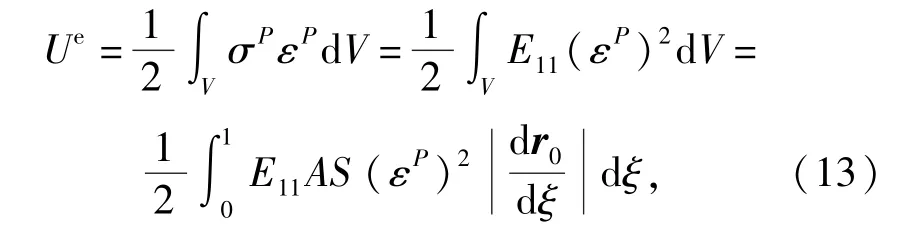
式中:AS为绳索的截面面积。

单元的质量矩阵为

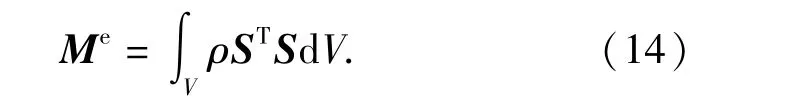
显然，单元质量矩阵仅与材料密度与单元形函数有关，为常数矩阵。

2　捕获机构建模

机械臂末端捕获器以及捕获器套筒内的操作原理可简化为图3所示。根据操作原理，可将其简化为“一杆、二环、三绳索”模型，如图4所示。“一杆”即捕获抓杆，固定在被捕获卫星上，其组成材料为铝合金。“二环”即固定环和旋转环，固定环固定在机械臂末端的套筒内，旋转环可沿着套筒内壁旋转。“三绳索”即连接固定环和旋转环的3根绳索，每根绳索的两端分别固定在固定环和旋转环上，初始时呈圆柱螺旋线，处于由两圆环组成的圆柱面上，且关于两圆环的共同轴线呈120°旋转对称，以获得尽可能大的捕获容差。

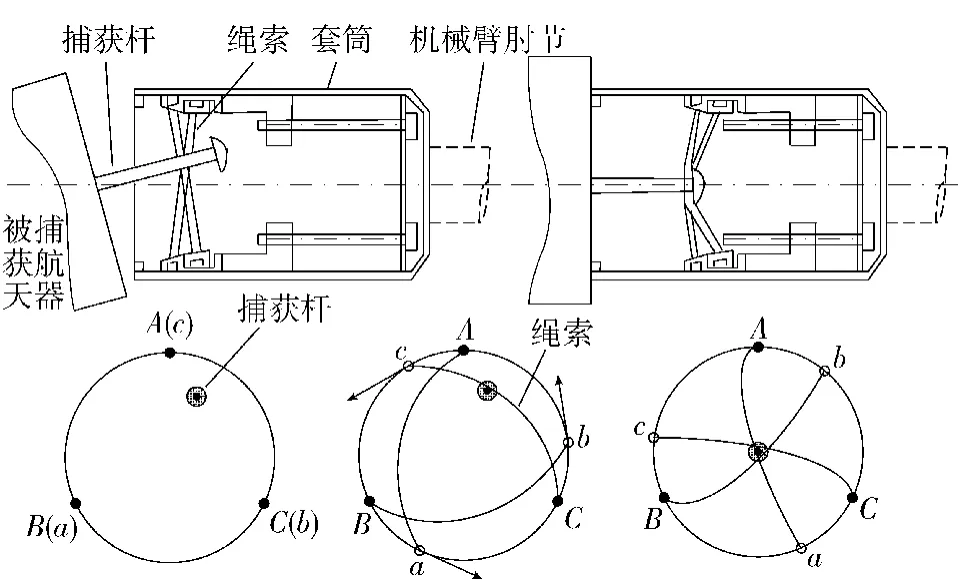
图3　捕获器操作原理示意图Fig.3 Schematic diagram of capture operating principle

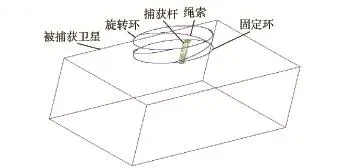
图4　“一杆、二环、三绳索”简化模型Fig.4 “One bar-two rings-three ropes”simplified model

当捕获杆进入套筒内绳索所围成的包络区域内时，启动捕获装置。在驱动传动系统的作用下，旋转环沿圆周旋转，使得3根绳索收拢并接触捕获杆。在接触力的作用下，捕获杆向3根绳索构成的中心移动。在3根绳索完全收拢并接触捕获杆后，捕获杆位置已矫正且不能逃逸，驱动制动系统制动旋转环以保证绳索不能继续运动，实现对捕获杆的捕获。

被捕获卫星星体尺寸设计为1m×1m×1m，质量为2 400 kg，可视为漂浮于无重力空间中的刚体。固定在其上的捕获抓杆尺寸为φ0.04m×0.35m，质量为1 kg，弹性模量EA=66.7GPa，泊松比vA=0.33.两圆环的半径R=0.72/π≈0.2292m，共用同一中心对称轴，固定环在卫星一侧，两环之间距离H=0.2m，可分别视为固定在套筒内和可沿套筒内壁旋转的刚体。3根柔性绳索的截面半径为0.001 m，轴向弹性模量E1=130GPa，横向弹性模量E2=0.13GPa，轴向与横向之间泊松比v21=0.34.由于捕获杆的弹性模量远大于绳索的横向弹性模量，故捕获杆可视为刚体。

为描述系统内各刚体和柔性体的运动，定义固定坐标系OXYZ和卫星连体坐标系O"X"Y"Z"，如图5所示，连体坐标系O"位于卫星的质心，各坐标轴均为卫星的中心惯量主轴，各中心主惯量矩为Jx=Jy=400.2 kg·m2，Jz=400.002 kg·m2，卫星相对质心O"的惯量张量J=diag（Jx，Jy，Jz）。固定坐标系O点位于固定环的圆心，OZ轴位于两圆环的中心对称轴上，初始时OX轴与O"X"轴平行。O"在固定坐标系中的坐标为（0m，0m，-0.6m），故将坐标系OXYZ沿着OZ轴负向平移0.6m便得到原点与O"重合的坐标系O′X′Y′Z′，坐标系O′X′Y′Z′至卫星连体坐标系O"X"Y"Z"之间的变换可采用卡尔丹角描述。设卡尔丹角为α、β、γ，则两坐标转换矩阵为

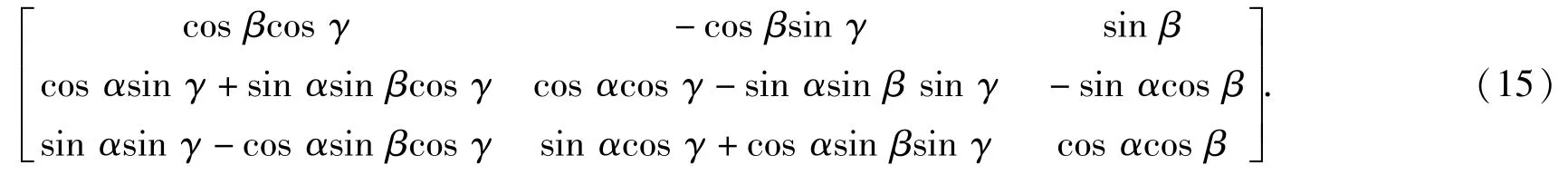
3　绳索及卫星的动力学方程描述

对于绳索与捕获杆之间的接触力，基于Hertz线接触模型［17］和Lankarani接触模型［18］中的能量耗散理论，本文提出一种可以考虑接触过程中能量耗散的法向线接触力计算模型:

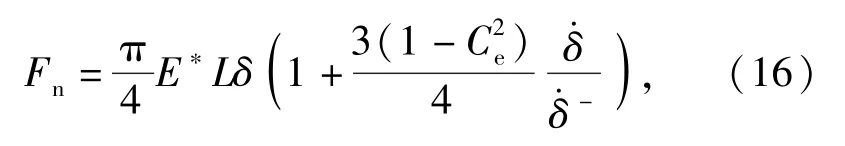
式中:Ce为碰撞恢复系数，为减少回弹，本文定为0.1；δ为接触过程中的嵌入深度为接触过程中的相对嵌入速度，在接触过程中这两者均不断变化；为接触前瞬间的相对嵌入速度，在某一碰撞过程期间其值是常数；L为线接触长度；E*为等效弹性模量，可由（17）式确定:

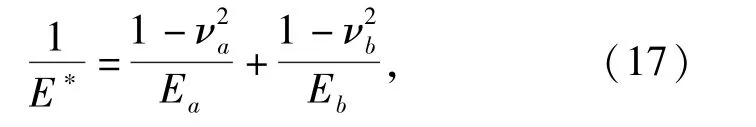
Ea和Eb分别是两个接触物体的弹性模量，va和vb分别是两个接触物体的泊松比。

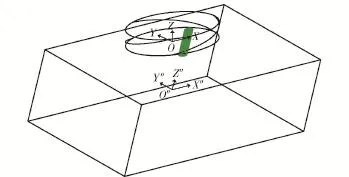
图5　固定坐标系和连体坐标系示意图Fig.5 Fixed frame and body frame

按照有限元法中的单元组装过程，可得到每根绳索的质量矩阵、刚度矩阵、广义外力向量、弹性力向量，再考虑到每根绳索的约束条件，采用第一类Lagrange方程建立每根绳索的动力学方程为

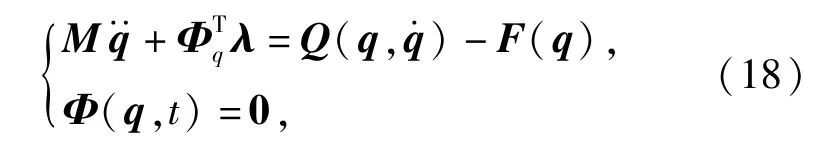
式中:M为每根绳索质量矩阵；q为每根绳索的广义坐标向量；F为每根绳索的弹性力向量；Q为每根绳索的广义外力向量；Φ和Φq分别为每根绳索的约束方程及其对广义坐标的Jacobi矩阵；λ为Lagrange乘子向量。

每根绳索共有6个约束方程，前3个约束使绳索一端固定在固定环上并保持静止，后3个约束使绳索另一端固定在旋转环上并随旋转环一起转动，旋转环的转动角度设计为

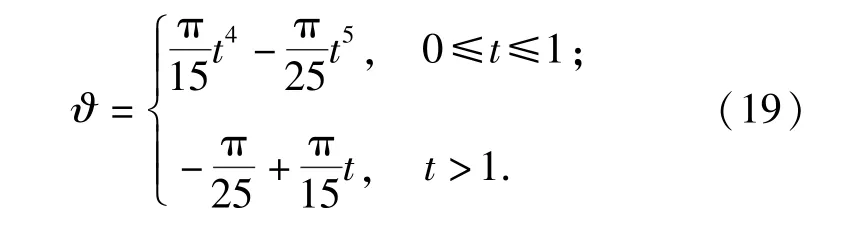
对于此3根绳索的微分代数方程组，即（19）式，本文采用了Arnold等［19］提出的广义α法迭代策略，为提高计算效率，结合了Bottasso等［14］提出的Scaling缩放技术，缩放系数取10-12.

下面研究被捕获卫星的姿态参数。记3根绳索作用在捕获杆上的接触力总和为FN，FN对卫星质心的矩为M，卫星在连体坐标系中的转动角速度为w，则卫星转动的动力学方程为

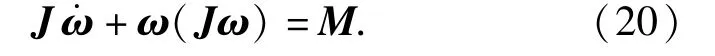
依据刚体动力学，卫星转动的运动学方程为

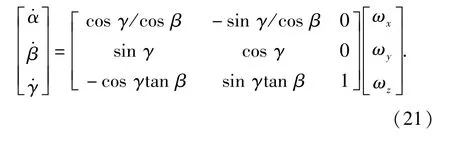
由（20）式、（21）式并结合卫星的初始姿态构型，经数值计算可得卡尔丹角α、β、γ，从而获得卫星的姿态参数。

图6表示以上两类系统动力学方程的联合求解过程。

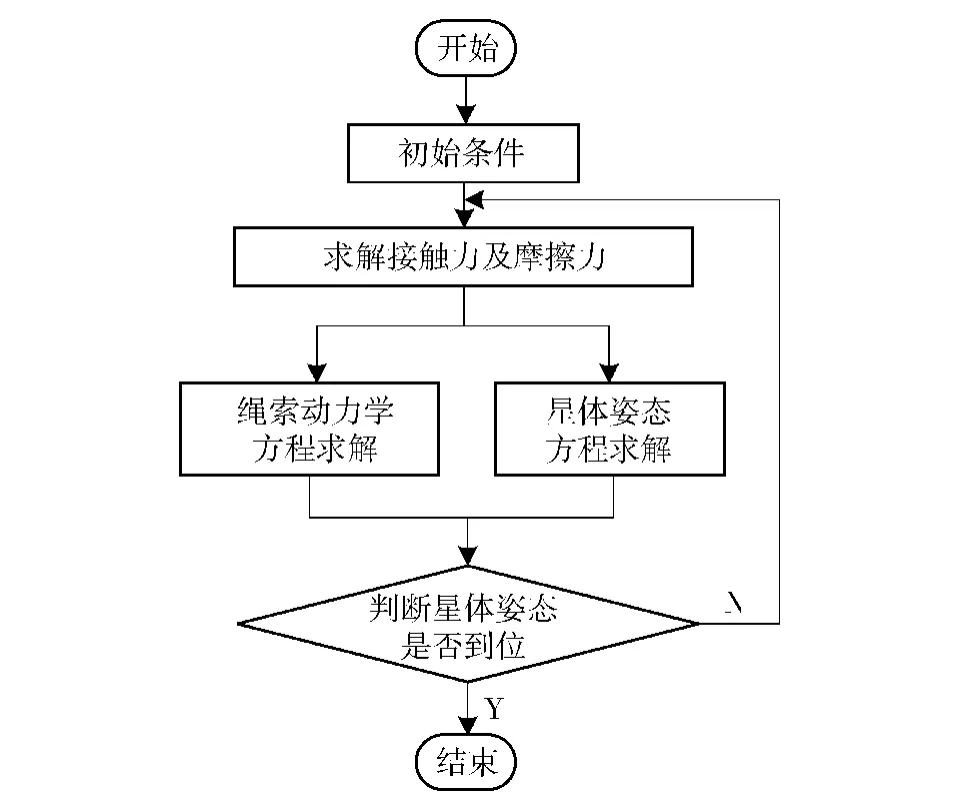
图6　系统动力学方程求解流程图Fig.6 Flow chart of solution of system dynamic equations

4　仿真计算结果与分析

由于捕获杆进入套筒内绳索所围成的包络区域内的随机性，本文考虑到较不理想情况，捕获杆与两圆环中心轴线之间夹角为较大值10°，捕获杆沿着两圆环中心轴线每旋转30°为一工况，共有12种工况。考虑到旋转对称性，只需对其中4种工况进行仿真，又考虑到等效性，捕获杆沿着两圆环中心轴线旋转，等效于各圆环及绳索共同沿着两圆环中心轴线反向旋转，这4种工况的各绳索初始状态在固定坐标系OXYZ中的描述为

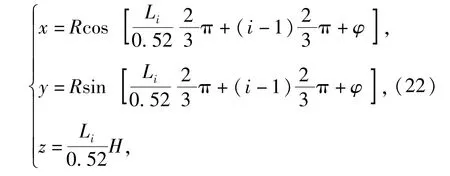
式中:i=1，2，3为绳索的序号；Li为初始时第i根绳索上某点到固定环起始点的绳长，0 m≤Li≤0.52m；φ为各圆环及绳索共同沿着两圆环中心轴线的旋转角，取-30°、0°、30°、60°为对应的4种工况。这4种工况的卡尔丹角初值均为α=10°，β= 0°，γ=0°.将每根绳索均匀分为10个ANCF单元。图7为φ=0°时绳索捕获过程各时刻状态图。

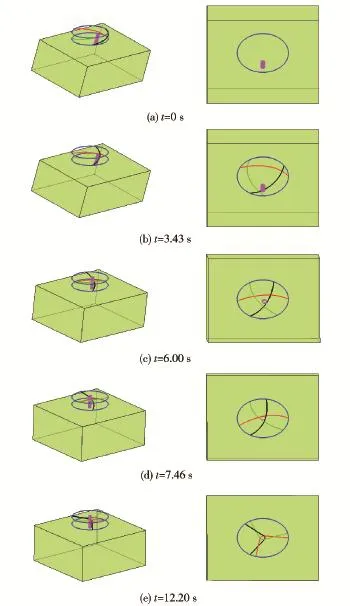
图7　绳索捕获过程示意图（左为三维图，右为俯视图）Fig.7 Schematic diagram of rope capture process（left:3-D view；right:top view）

由图7可知，在t=3.43 s时，第3根绳索首先接触到捕获杆，系统产生接触碰撞力并伴随能量耗散。随着3根绳索的收拢，所围区域逐渐变小，捕获杆向中间靠拢。到t=7.46 s时，3根绳索都接触到捕获杆，之后在3根绳索的接触力共同作用下，捕获杆的方位不断得到矫正。最终在t=12.20 s时，捕获杆位置已矫正且不能逃逸。一般要求捕获杆中心轴与两圆环中心轴之间夹角小于0.3°.

设捕获杆中心轴即O"Z"与两圆环中心轴即OZ之间夹角为θ、卫星在OZ方向上所转角度为ψ.θ、ψ与卡尔丹角α、β、γ之间的关系为

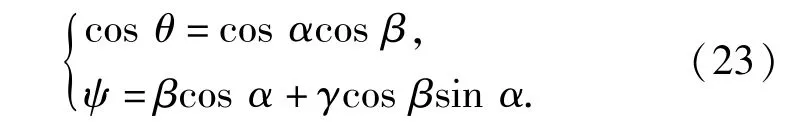
图8是旋转角φ分别为-30°、0°、30°、60°时所对应的4种工况下θ、ψ随时间t的变化曲线。

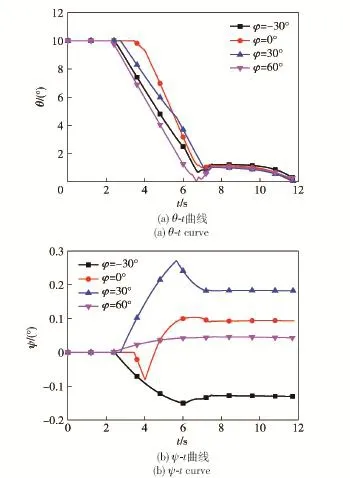
图8　卫星各姿态角随时间变化曲线Fig.8 Satellite attitude angle versus time

由图8可知，捕获杆中心轴与两圆环中心轴之间的夹角θ大体上逐渐减小，经矫正后θ均小于0.3°，符合要求。在不同工况下，卫星在OZ方向上所转角度ψ变化趋势不同，最终值也不同，但其绝对值均小于0.2°，属于误差范围内。

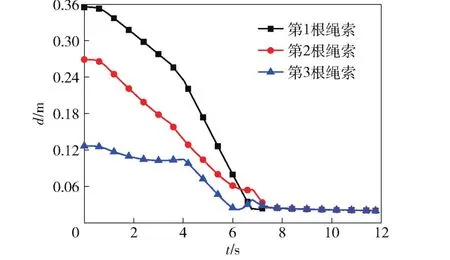
图9　各绳索中点与捕获杆中心轴的距离随时间变化曲线Fig.9 Distance between rope midpoint and capture pole central axis versus time

以旋转角φ为0°这一工况为例，研究捕获过程中绳索的运动和力情况。图9为3根绳索的中点与捕获杆中心轴的距离d随时间变化曲线，由图9可知，绳索中点均不断靠近捕获杆中心轴，最后与中心轴的距离均为捕获杆半径0.02 m.图10为3根绳索的绳长LC随时间变化曲线，由图10可知，绳索与捕获杆接触后绳长均略伸长，在3根绳索均与捕获杆接触后的矫正阶段伸长量变大，但最终的伸长量均不超过原绳长的1.5％.

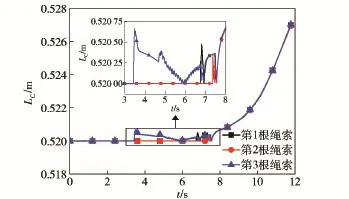
图10 各绳索绳长随时间变化曲线Fig.10 Cord length versus time

图11（a）为在固定端附近3根绳索拉力随时间的变化曲线，图11（b）为在旋转环连接端附近3根绳索拉力随时间的变化曲线，由图11可知，绳索与捕获杆接触后，绳索的首末两端拉力均在500 N以内。在3根绳索均与捕获杆接触后的矫正阶段，首末两端的拉力快速增大，但固定端3根绳索的拉力均在5 400N之内，旋转端3根绳索的拉力均在5 780 N之内。该结论可以为柔性绳索的选取和设计提供参考。

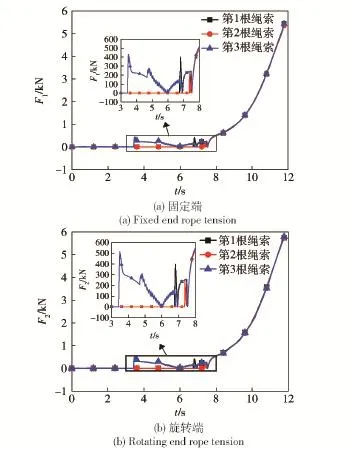
图11　各绳索固定端和旋转环连接端拉力随时间变化曲线Fig.11 Fixed end rope tension and rotating end rope tension versus time

5　结论

本文采用ANCF和卡尔丹角以及非线性接触碰撞力模型，建立了空间机械臂绳索类末端捕获机构捕获卫星过程的刚柔耦合动力学模型。结合广义α法以及工程上常用的Scaling技术，利用Matlab开发了相应的计算程序，实现了动力学方程的高效精确数值求解。计算结果能够较好地模拟绳索缠绕及捕获卫星这一完整过程，使卫星从偏差位置、姿态下矫正到目标位置且不能逃逸，姿态绝对值在误差范围之内；同时研究了绳索首末端的拉力情况，计算结果表明，在3根绳索均与捕获杆接触后的矫正阶段，首末两端的拉力快速增大了一个数量级，为实际工程中柔性绳索的抗拉能力设计提供一定参考。本文给出的多种工况仿真实例说明了该方法的有效性。

（References）

［1］ 阳光.日本新型火箭发射空间站货运飞船［J］.中国航天，2009（10）:19-27. YANG Guang.Japan's new rocket launch spaceship［J］.China Aerospace，2009（10）:19-27.（in Chinese）

［2］ 陈杰.美国"龙"飞船国际空间站对接试验简析［J］.中国航天，2012（8）:24-29. CHEN Jie.America's“dragon”spaceship dock with the international space station test analysis［J］.China Aerospace，2012（8）: 24-29.（in Chinese）

［3］ Fehse W.Automated rendezvous and docking of spacecraft［M］. Cambridge:Cambridge University Press，2003.

［4］ 于洋，宝音贺西，李俊峰.空间绳索系统的动力学建模方法［C］∥北京力学会第16届学术年会.北京:北京力学会，2010. YU Yang，BAOYIN He-xi，LI Jun-feng.Space rope system dynamics modeling method［C］∥16th Annual Seminar of Beijing Society of Theoretical and Applied Mechanics.Beijing:Beijing Society of Theoretical and Applied Mechanics，2010.（in Chinese）

［5］ 陈钦，杨乐平.空间绳网系统发射动力学问题研究［J］.宇航学报，2009，30（5）:1829-1833. CHEN Qin，YANG Le-ping.Research on casting dy-namics of orbital net systems［J］.Journal of Astro-nautics，2009，30（5）: 1829-1833.（in Chinese）

［6］ 谭益松，刘伊威，刘宏，等.空间大型末端执行器柔性钢丝绳的建模与捕获动力学［J］.机器人，2011，33（2）:156-160. TAN Yi-song，LIU Yi-wei，LIU Hong，et al.Modeling and capture dynamics of flexible cables used in large-scale space end-effector［J］.Robot，2011，33（2）:156-160.（in Chinese）

［7］ Shabana A A，Yakoub R Y.Three dimensional absolute nodal co-ordinate formulation for beam elements:Theory［J］.Journal of Mechanical Design，2001，123（4）:606-613.

［8］ 杨永泰，荣吉利，李健，等.双柔性空间机械臂动力学建模与控制［J］.兵工学报，2014，35（7）:1003-1008. YANG Yong-tai，RONG Ji-li，LI Jian，et al.Dynamic modeling and control of space manipulator with flexi-ble joints and links［J］.Acta Armamentarii，2014，35（7）:1003-1008.（in Chinese）

［9］ 朱大鹏.多体动力学框架下的大变形曲梁单元及其应用［D］.北京:清华大学，2008. ZHU Da-peng.The large deformation curved beam element in multibody dynamics and its application［D］.Beijing:Tsinghua U-niversity，2008.（in Chinese）

［10］ 潘冬，张越，魏承，等.空间大型末端执行器绳索捕获动力学建模与仿真［J］.振动与冲击，2015（1）:74-79，189. PAN Dong，ZHANG Yue，WEI Cheng，et al.Dynamic modeling and simulation on rope capturing by space large end effector［J］. Journal of Vibration and Shock，2015（1）:74-79，189.（in Chinese）

［11］ Zhang Y，Wei C，Pan D，et al.A dynamical approach to space capturing procedure using flexible cables［J］.Aircraft Engineering and Aerospace Technology，2016，88（1）:53-65.

［12］ 潘冬，魏承，田浩，等.空间大型末端执行器捕获动力学与实验研究［J］.宇航学报，2014，35（10）:1120-1126. PAN Dong，WEI Cheng，TIAN Hao，et al.Capturing dynamics and experiment of the space large end ef-fector［J］.Journal of Astronautics，2014，35（10）:1120-1126.（in Chinese）

［13］ Chung J，Hulbert G.A time integration algorithm for structural dynamics with improved numerical dissipa-tion:the generalized-a method［J］.Journal of Applied Mechanics，1993，60（2）:371-375.

［14］ Bottasso C L，Dopico D，Trainelli L.On the optimal scaling of index three DAEs in multibody dynamics［J］.Multibody System Dynamics，2008，19（1）:3-20.

［15］ Gerstmayr J，Irschik H.On the correct representation of bending and axial deformation in the absolute nodal coordinate formulation with an elastic line ap-proach［J］.Journal of Sound＆amp;Vibration，2008，318（3）:461-487.

［16］ 刘铖.基于绝对坐标描述的柔性空间结构展开动力学研究［D］.北京:北京理工大学，2013. LIU Cheng.Deployment dynamics of flexible space structures described by absolute-coordinate-based method［D］.Beijing:Beijing Institute of Technology，2013.（in Chinese）

［17］ Reis V L，Daniel G B，Cavalca K L.Dynamic analysis of a lubricated planar slider-crank mechanism consid-ering friction and Hertz contact effects［J］.Mechanism＆amp;Machine Theory，2014，74（6）:257-273.

［18］ Lankarani H M，Nikravesh PE.A contact force model with hysteresis damping for impact analysis of multi-body systems［J］. ASME Journal of Mechanical Design，1990，112（3）:369-376.

［19］ Arnold M，Bruls O.Convergence of the generalized-a scheme for constrained mechanical systems［J］.Mul-tibody System Dynamics，2007，18（2）:185-202.

Capturing Dynamics of Flexible Ropes for Space Large-scale End Effector

RONG Ji-li1，XIN Peng-fei1，ZHUGE Xun2，YANG Yong-tai3，XIANG Da-lin1
（1.Department of Mechanics，School of aerospace Engineering，Beijing Institute of Technology，Beijing 100081，China；2.Beijing Aerospace Propulsion Institute，Beijing 100076，China；3.Quanzhou Institute of Equipment Manufacturing，Chinese Academy of Sciences，Quanzhou 362000，Fujian，China）

The problems of dynamics during winding and capturing a satellite by the space manipulator end-effector are studied.The winding movement of transverse isotropic flexible wire ropes is described by absolute nodal coordinate formulation（ANCF），and Cardan angles are applied to describe the attitude of the rigid satellite.A rigid-flexible coupling dynamic model containing a stationary ring and a rotation ring fixed on the end-effector，three ropes and a shaft of the captured satellite is established.Nonlinear contact force is introduced to reveal the interaction between shaft and wire ropes.The generalized-α method and the scaling technique are employed to develop a numerical calculation program for solving the dynamic equations precisely and efficiently.Simulation results show that the proposed dynamic model can preferably simulate the processes of flexible wire rope winding and satellite capturing.The change of satellite attitude and rope movement during capturing are obtained，which could provide reference basis for design and test of capturing mechanism.

basic disciplines of aerospace science and technology；capturing dynamics；flexible rope；satellite attitude；rigid-flexible coupling；absolute nodal coordinate formulation

V414.1

A

1000-1093（2016）09-1730-08

10.3969/j.issn.1000-1093.2016.09.025

2015-12-26

国家自然科学基金项目（10972033）；中国航天科技集团公司航天科技创新基金项目（CAST20100141107）

荣吉利（1964—），男，教授，博士生导师。E-mail:rongjili@bit.edu.cn