基于冲击响应谱特征提取的自动机裂纹故障诊断

李海广，潘宏侠，任海锋

（1.中北大学机电工程学院，山西太原030051；2.内蒙古科技大学内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室，内蒙古包头014010）

基于冲击响应谱特征提取的自动机裂纹故障诊断

李海广1，2，潘宏侠1，任海锋1

（1.中北大学机电工程学院，山西太原030051；2.内蒙古科技大学内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室，内蒙古包头014010）

针对武器自动机在动作过程中，机构相互碰撞产生的冲击振动信号，提出计算冲击振动信号的冲击响应谱，并提取冲击响应谱特征值，进而开展自动机部件裂纹故障识别的新方法。开展不同裂纹部件的射击试验，采集正常及故障条件下自动机部件碰撞冲击信号，并根据运动过程进行分离；计算分离后冲击信号最大冲击响应谱，根据冲击响应谱不同区域的冲击响应特征参数，提出冲击响应谱相对峰值比和相对峰值频率比的定义，并将相对峰值比、相对峰值频率比作为故障特征值进行提取；在不同裂纹故障条件下，对比故障特征值统计分布形态，完成不同故障条件的识别试验。试验结果表明，冲击响应谱特性提取可以准确有效地诊断自动机裂纹故障，是一种可以用来在线监测的新方法。

兵器科学与技术；故障诊断；运动形态；冲击响应谱；相对峰值比；相对峰值频率比

0　引言

自动机是自动武器的核心组成部分，完成重新装弹和发射下一发弹的全部动作，实现连续发射的各机构的组合［1］，其工作循环一般包括:击发、活动件后坐、开锁、退壳、复进、闭锁等主要过程，正常的自动机表现出稳定性的运动特性［2］。在高温、高压、高冲击的工作环境下，自动机会出现停射、卡涩、射速偏低等故障［3］，其中裂纹及磨损等故障是影响工作可靠性的重要因素。传统的检测方法往往是将零部件解体，进行观察或利用超声［4］、涡流［5］、漏磁［6］等技术进行无损检测。然而随着信号处理、动态测试及传感器技术的发展，世界各国学者普遍重视能够在机械设备运转过程中，对机械设备发生异常的部位及异常发生的原因，进行精确分析诊断的新技术。振动信号含有丰富的反映机械工作状态信息，且易于获取，相关分析理论也相对成熟，因此利用振动信号进行故障诊断的技术最为普遍。其中振动信号对于裂纹等早期故障的预报研究中，李辉等［7］在齿轮传动系统、刘长利等［8］在转子系统研究中，均发现裂纹对振动特性的影响。自动机作为一个复杂的机械系统，其振动特性为高强度的短时冲击信号，当构件出现裂纹等故障时也会影响其冲击响应信号的频率、能量特性。文献［9-12］提出采集自动机射击工作过程中的冲击振动信号，使用经验模式分解（EMD）［10］、局域波［11-12］等信号分解方法，找到故障信息敏感的信号分量，再提取故障特征值进行模式识别的自动机裂纹故障识别方法。然而这类识别方法的最大缺陷是在故障分量的选择中存在主观因素，不同分解方法通常选择不同的故障分量，同时造成模式识别的困难。在冲击振动信号的研究领域中，冲击响应谱是将冲击振动信号整体作为研究对象，因此本文提出利用冲击响应谱提取故障信息的新方法。冲击响应谱是将冲击信号输入到一个单自由度的振动系统，得到该系统在不同自然频率下的相应峰值，由布洛特于1963年提出。冲击响应谱广泛应用于冲击试验，模拟真实的冲击环境，表征冲击作用效果，如包装货品跌落［13］、火箭发射［14］、飞机着陆［15］等。也有学者指出冲击响应谱特征能够反映出真实冲击信号的特性［16］，能够用于不同冲击过程的比较［17］，但这一研究领域还未引起广大学者的重视，基于冲击响应谱的故障信号识别工作还未广泛开始。

本文基于冲击响应谱能够反映出冲击信号特征的特性，将冲击响应谱的应用范围衍生到故障处理领域。利用自动机在工作循环的每个分解过程中，形成的冲击振动信号为分析对象，通过计算冲击信号的最大冲击响应谱，分析冲击响应谱在不同区域的冲击响应特征值。提出相对峰值比，相对峰值频率比的定义，并作为故障特征值进行提取，利用特征值分布特性进行不同故障类型的识别。故障对比试验结果表明，该方法可以简单、有效、客观地反映出故障信息，鉴于冲击响应谱是冲击振动测量仪器的标准功能，因此本文提出的方法很容易在硬件设备中实现在线故障诊断。

1　理论基础

1.1冲击响应谱

冲击响应谱是基于冲击加速度时域数值的计算函数，主要思想是将冲击激励施加在一个标准的单自由度质量弹簧阻尼振动系统，如图1所示。每个单元由质量为mi的质块，刚度为ki的弹簧，和一个阻尼为ci的阻尼器组成的单自由度系统，每个单元系统阻尼比ξi是相等的。

将加速度信号作为基础激励源，质块的运动方程为

式中:x为质块的绝对位移；y为基座的位移。定义z=x-y为相对位移，（1）式转化为为系统的无阻尼自然频率系统阻尼比。

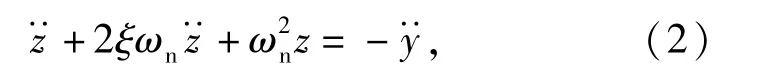
求解方程（2）式，可以得到冲击响应峰值与自然频率之间的函数，即该系统的冲击响应谱。目前应用较广泛的冲击响应谱算法是改进的递归数字滤波法［18］，该方法于1980年由Smallwood［19］提出。

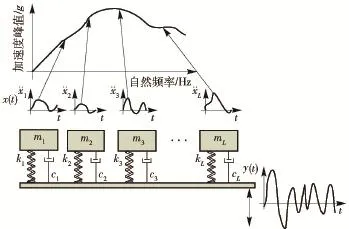
图1　冲击响应谱模型Fig.1 Shock response spectrum model

根据质块冲击响应参变量不同，冲击响应谱分为绝对加速度谱、相对位移谱；根据冲击作用时间冲击响应谱可以分为初始冲击响应谱、残余冲击响应谱、最大冲击响应谱；根据冲击响应参变量矢量方向，冲击响应谱可以分为正谱和负谱。由于冲击造成的损害程度正比于最大冲击响应，是否发生在冲击作用时间内并不重要。因此在实际使用中，每时刻正负谱的绝对峰值谱作为系统的最大冲击响应谱，各冲击响应谱的关系如图2所示，本文采用冲击响应谱为最大冲击响应谱。

图2　不同冲击响应谱关系图Fig.2 Links among different SRSs

1.2冲击响应谱区域特征

冲击响应谱能够反映冲击信号的特性，如图3中分别为振幅相等、时间间隔相同的矩形脉冲、正弦脉冲、后峰锯齿脉冲激励等作用下的冲击响应谱，通常整个谱线可以分为3个区域［20］，可以在不同区域进行谱特征提取。

1）脉冲区域。最大冲击响应谱数值小于冲击幅值，在对数坐标系下，谱线斜率理论上等于12 dB/oct，在实际应用中，该区域的斜率在6 dB/oct与12 dB/oct之间［16］，比较小的斜率是由于传感器缺陷产生基线漂移造成的。

2）静态区域。正谱冲击响应值在高频区域趋向于冲击幅值。

3）中间区域。最大冲击响应是冲击幅值动态放大，放大系数显著地依赖于冲击信号的形状和系统阻尼。Wright［16］针对不同冲击响应谱试验的数据验证中，阐明冲击谱中的加速度放大系数，即某一自然频率对应的加速度峰值与冲击信号峰值之比，不同冲击信号下，其取值范围为2～6之间。

在不同谱线区域可以提取不同的冲击响应谱特征值:在脉冲区域，对数坐标下谱线斜率可以表征冲击信号的对称性，如图3中，对称的正弦脉冲信号冲击响应谱斜率明显大于矩形脉冲等非对称脉冲信号；静态区域中最大自然频率所对应的峰值冲击响应谱可以表征冲击信号的幅值；中间区域内可以提取冲击响应谱线峰值，表征加速度放大系数（见图3），不同的冲击信号响应谱存在不同的冲击响应谱峰值。

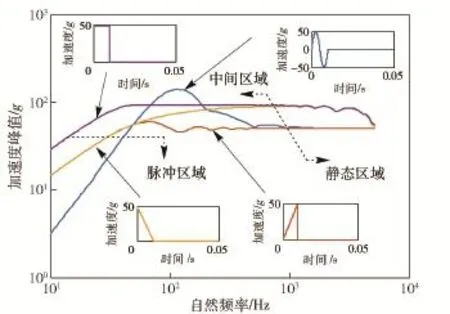
图3　不同冲击激励的冲击响应谱及谱区域划分Fig.3 Shock response spectra of different input pulses and spectra domains

2　试验研究

2.1自动机振动信号采集系统

本文试验研究的对象为某型高射机枪，如图4所示，采用导气式自动机。由于自动机的构成比较复杂，各个机构之间多是以曲面或者棱角的形式相接触，给布置测点安放传感器带来困难。经过对比自动机各机构的位置和考虑传感器安放的可行性，最终选择了在机枪尾部上方和机匣的前侧上方来布置测点，具体测点位置如图4所示。加速度传感器采用美国PCB公司350A14量程为10 000 g的单向加速度传感器，枪口正前方为x轴正方向，枪口左方向为y轴正方向，建立坐标系。本试验在机枪射击靶场进行，用比利时LMS系统进行信号的采集工作，设置采样频率为204.8 kHz.每个试验设计工况下，实弹射击依次按照单发、3连发、5连发顺序进行射击。

图4　试验高射机枪及测点布置Fig.4 Test machine gun and measuring point arrangement

2.2自动机运动形态分解

在自动武器发射过程中，自动机各部件能够按照给定的顺序，分时分段、有条不紊地参与整个自动机的工作。自动机运动形态分解的概念是:分析自动机完整、准确的运动过程，将动作过程中产生的冲击振动信号和运动过程相对应起来，有针对性地对冲击振动信号进行分析处理，从而得到自动机相关工作状态信息，形成一种自动机振动信息分析方法。图5为本文试验高射机枪自动机动作过程，在对其进行运动形态分解，以开闭锁过程为例。其开闭锁机构的动作过程分析如图6，图中:实线部分为开锁时机构件运动碰撞过程，机框向右运动开锁，主要撞击点如图所示有A、B两个位置；虚线部分为闭锁时机构件运动碰撞过程，机框向左运动闭锁，主要撞击点为C位置。

2.3基于运动形态振动信号

图7为本文试验在单发射击模式下的机匣前侧上方x轴方向振动时域图。由振动信号可以看出，信号具有很强的冲击特性，能量在撞击后出现峰值，之后迅速地衰减，而每一次撞击正是完成自动机运动循环的一环节，而基于每个循环环节的振动信号特征提取，进而开展自动机工作状态的研究，正是本文提出的运动形态分解的概念。

图7中撞击1:机框撞击闭锁片（闭锁撞击）；撞击2:机框撞击击针（击发撞击）；撞击3:机框撞击闭锁片（开锁撞击）；撞击4:抽壳撞击；撞击5:抛壳撞击；撞击6:后坐到位撞击。过程1为闭锁过程，过程2为开锁过程，过程3后坐到位撞击过程。

图5　自动机运动形态分解Fig.5 Operation status decomposition of gun automatic mechanism

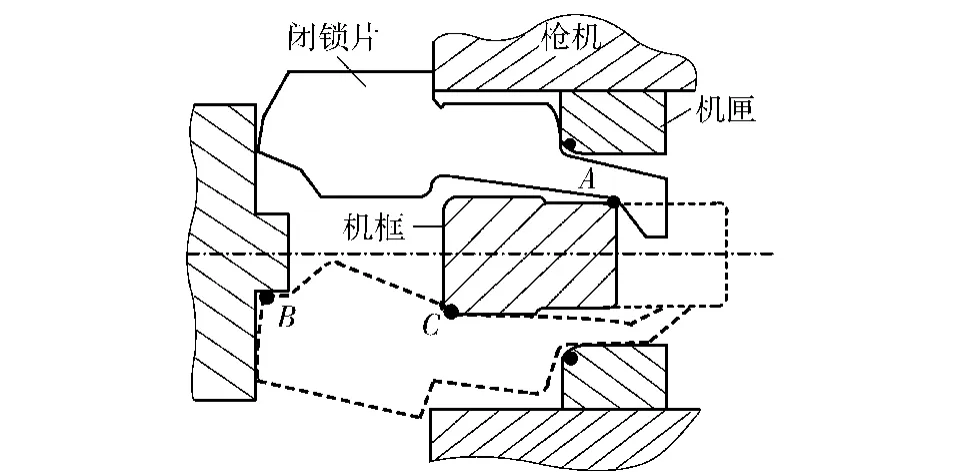
图6　开闭锁碰撞动作示意图Fig.6 Locking or unlocking collision process

2.4故障设置

本次试验共设置了两种故障，其中对闭锁片故障设置一种，枪击框故障一种。分别为:故障1是在开锁时闭锁片旋转与机枪框接触的部位，即沿经过闭锁片回转圆心且垂直于闭锁片内平面的方向，设置1.5mm深的裂纹槽；故障2即为机头左右两侧的圆角矩形窗后端的两对圆角上，沿圆角直径各呈正负45°切入1.5mm深的裂纹槽，如图8所示。

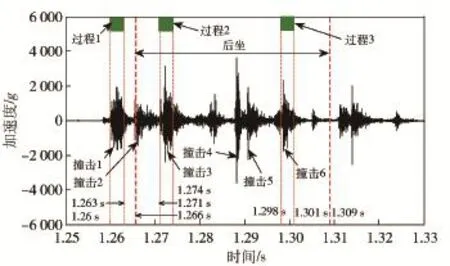
图7　单发模式振动信号基于运动形态分解Fig.7 Single-shot vibration signals based on operation status decomposition

图8　不同部件故障裂纹位置Fig.8 Different crack locations on different parts

每一种故障模式下:实弹射击模式为单发射击，射击3次，共3发子弹；3连发射击模式，射击两次，共6发子弹；5连发射击模式，射击一次，5发子弹。在两种故障和正常试验模式下，共射击42发子弹。

2.5故障振动信号截取

由于本次试验故障设置在闭锁片和枪机上，而闭锁片和枪机的主要动作是在闭锁行程和开锁行程完成的。根据位置关系，机匣的前侧测点测量开闭锁撞击信号比较明显，而且闭锁冲击振动信号前有一段自由行程，加速度信号保持在0 g附近，整个闭锁冲击信号很容易分离下来。

由于单发射击及连发第1发射击时，各个机构件之间有很大的空隙。但在连发射击模式，第1发子弹的作用力后，各机构件之间的空隙被很大地压缩了，构件之间振动约束增强，冲击振动时间减少，造成单发及第1发子弹与后续连发子弹闭锁冲击信号作用时间不同。如正常模式下，第1组3连发子弹的第1发和第2发闭锁x方向冲击振动信号，如图9所示。考虑到连发模式下，第2发及后续子弹的冲击振动信号会受到前1发的影响，故本文振动信号截取单发及连发第1发子弹闭锁x方向冲击信号。

图9　闭锁冲击信号时域图Fig.9 Time domain signals from unlocking collision

2.6冲击响应谱的计算

1）冲击响应谱参数选取。由（2）式可知计算冲击响应谱需要选取质块系统的阻尼比ξ和一组自然频率ωn，由于本文是基于不同冲击信号的冲击响应谱比较，阻尼比ξ的选取对于不同冲击谱比较影响比较小，本文选取ξ=0.05.虽然任何一组自然频率ωn都可以用来计算冲击谱响应，但由图3可知，自然频率的选择影响到了谱线在不同区域的分布，本文选取质块自然频率初始值为100 Hz.最大自然频率选择采集频率的1/8，倍频为21/6，即自然频率序列ωn为100 Hz、105.95 Hz、112.25 Hz、118.92 Hz、…、100×21/6（N-1）Hz，这里N=98，冲击响应谱的计算采用递归数字滤波法。

2）冲击响应谱的区域分析。计算故障模式及正常模式下，闭锁振动冲击信号的最大冲击响应谱，由于每一种故障模式共有6发子弹，产生6条不同的冲击响应谱线。如图10所示，由图10中可发现，不同故障模式下，最大冲击响应谱呈现出较一致的脉冲区域，不同形态的静态区域和中间区域，其中:正常模式下，自然频率104Hz附近，存在具有明显峰值的中间区域，超过104Hz后为静态区域；故障1模式下的中间区域不明显，超过104Hz，冲击响应幅值仍然增加；故障2模式下在104Hz附近，冲击响应幅值基本保持不变，处于中间区域。

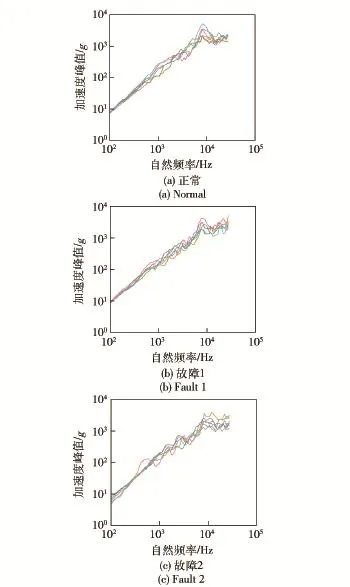
图10　不同故障模式下的子弹冲击响应谱Fig.10 Shock response spectrum of the first bullet under different fault conditions

2.7冲击响应谱故障特征提取

由图10分析可知冲击响应谱线在不同故障模式下主要差异表现为:是否出现明显的静态区域和放大区域。经过比较分析故障模式及正常模式冲击响应谱线，可以发现不同的故障模式对应3条典型的不同冲击响应曲线，如图11所示。图11（a）最大冲击响应峰值发生低于最大自然频率的某个中间频率，峰值之后呈下降趋势；图11（b）为中间区域最大冲击响应峰值发生在最大自然频率附近，整体曲线呈现上升趋势；图11（c）在最大频率附近，冲击响应值保持基本不变。

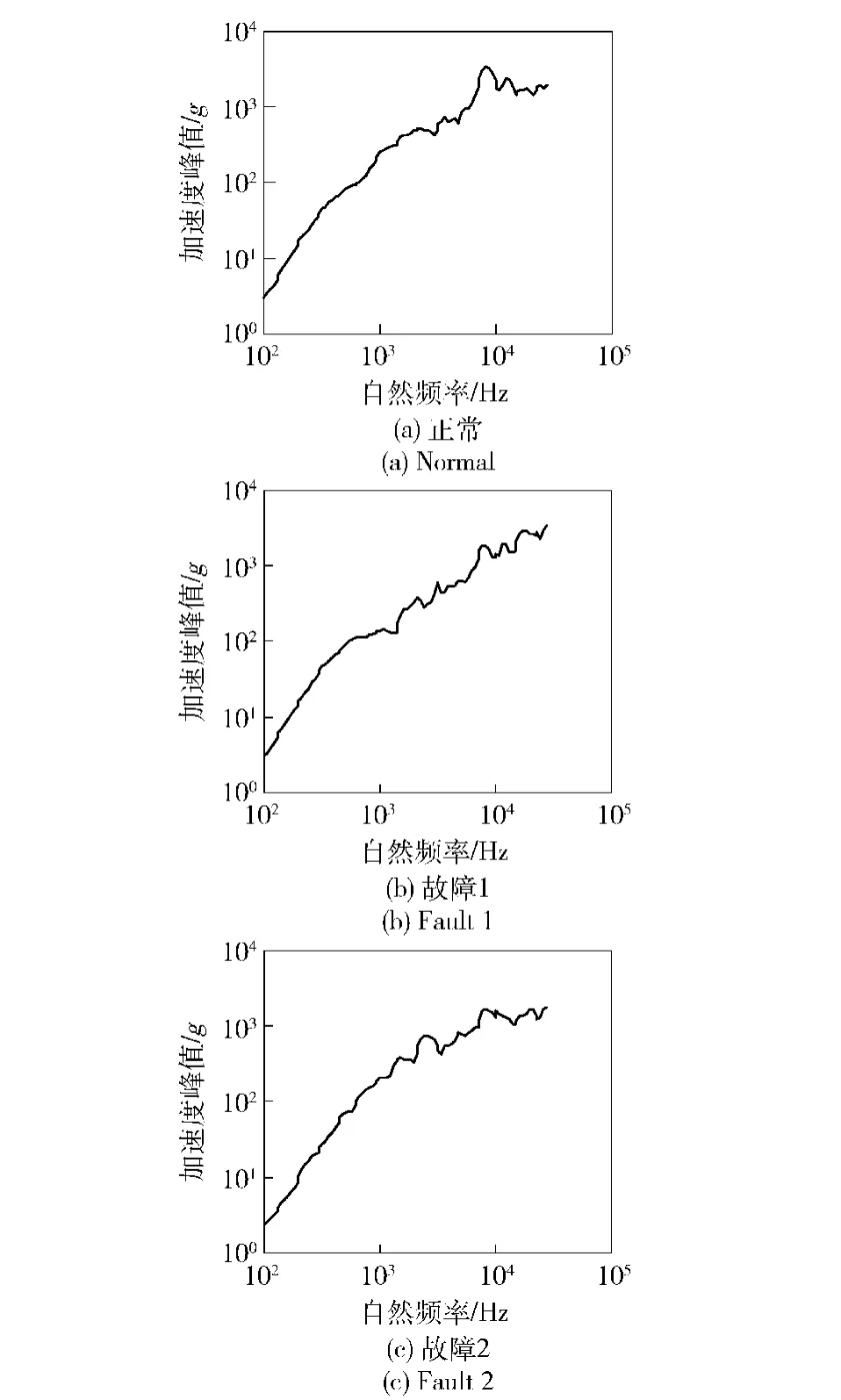
图11　典型的不同冲击响应谱线形状Fig.11 Typical shock response spectrum line shapes

观察图11中3条不同冲击响应谱曲线形状，结合1.2节冲击响应谱不同区域的划分方法，可知3条冲击响应谱曲线的不同，主要体现为中间区域与静态区域的不同。但仅仅使用1.2节提出的谱线斜率、谱线峰值、最大自然频率冲击响应值等冲击响应谱特征值，无法确定谱线峰值位置及谱线变化规律，还不足以区分这3条冲击响应谱曲线。为了区分不同区域划分，可以提取以下主要参数:冲击响应峰值Gmax及其对应的自然频率FnGmax，最大自然频率Fnmax及最后n个连续冲击响应值的平均值。n的取值范围可以通过观察冲击响应谱整体趋势确定，本文设定为自然频率序列N的1/5，如图12所示。

图12　冲击响应谱线特征参数提取Fig.12 Feature extraction of different shock response spectra

定义相对峰值比Gr、相对峰值频率比Fnr为

根据定义可知，Gr取值范围大于等于1，Fnr的取值范围小于等于1.相对峰值比Gr为相应谱峰值与后连续n个冲击响应值平均数之比，Gr的大小可以表征峰值的存在及其大小，Gr≫1说明峰值明显存在。相对峰值频率比Fnr为冲击响应谱峰值频率与最大自然频率之比，其大小可以表征峰值位置，Fnr≪1说明峰值位置远离最大自然频率。图11（a）为中间区域+静态区域的典型谱线，冲击响应峰值明显大于最后n个冲击响应幅值的平均值，而峰值频率远离最大自然频率，故Gr大于1，而Fnr明显小于1.图11（b）为完全中间区域典型谱线，冲击响应峰值接近最大自然频率冲击响应值，且大于最后n个冲击响应幅值平均值，故Gr大于1，峰值频率接近最大自然频率，Fnr接近1.图11（c）是过渡中间区域，冲击响应峰值与最后n个冲击响应幅值的平均值较接近，峰值频率的取值范围比较大，故Gr略大于1，Fnr小于1.根据上述分析，图11中3种不同冲击响应谱线上，使用Gr、Fnr提取相应谱线特征，结果如表1所示。

表1　冲击响应谱不同区域特征提取Tab.1 Feature extraction of shock response spectra from different spectra domains

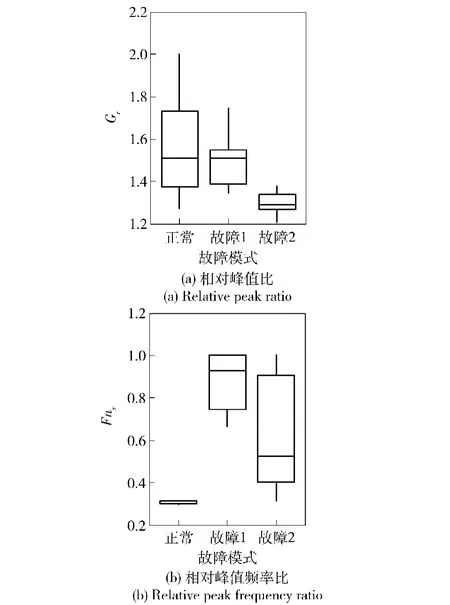
图13　不同故障模式下Gr、Fnr分布特性Fig.13 Distribution characteristics of Grand Fnrin different fault modes

计算图10所示在不同故障模式下冲击响应谱的故障特征值:相对峰值比Gr、相对峰值频率比Fnr，其中n的取值范围N/5=98/5≈20.观察特征值的分布特性，绘制不同故障模式下Gr、Fnr的分布箱线图，如图13所示，以进行故障类型的识别。从图13可以清楚地观察到正常模式下，Gr取值范围分布在1.3～2.0内，而Fnr取值集中分布在0.2附近。对照表1，可以判断:正常模式下，谱线处于中间区域+静态区域的状态；故障1模式下，Gr取值范围分布在1.4～1.7内，Fnr取值集中分布在0.7～1.0内，接近1.0，对照表1可以判断故障1模式的谱线处于完全中间区域；故障2模式下，Gr取值主要分布在1.3附近，而Fnr取值主要分布在0.2～1.0内，对照表1，同样可以判定故障2模式的谱线处于过渡中间区域。从图13中还可以观察到，每种故障工况下，并不是每发子弹均存在与总体趋势相一致的谱线区域规律，考虑的原因是子弹个体的差异，如质量、弹药量不同，对射击过程中冲击振动信号产生一定的影响。

对比图8不同部件故障裂纹位置，故障1为闭锁片裂纹故障，故障2为枪击框裂纹故障。图13中Gr、Fnr的分布规律可以准确区分正常及两种故障模式，说明冲击响应谱故障特征参数Gr、Fnr的分布特征可以有效地揭示故障的发生及故障位置的不同。进而验证了本文提出利用高速自动机动作时的碰撞冲击信号，通过提取冲击响应谱故障特征参数，开展故障识别的方法是完全有效的。

3　结论

1）基于自动机动作过程的运动分解，测量动作过程中部件上的短时冲击振动信号，计算冲击信号的最大冲击响应谱，在不同裂纹故障模式下冲击响应谱形态呈现出不同区域划分的特点。

2）本文定义:最大冲击响应谱的相对峰值比，即冲击响应峰值与最后n个冲击响应值的平均值之比；相对峰值频率比，即冲击响应峰值所对应的自然频率与最大自然频率之比。通过对相对峰值比、相对峰值频率比取值范围分析，可以确定冲击响应谱线的基本形态，如完全中间区域、静态区域等。

3）基于不同部件、不同裂纹故障条件下，测取每发子弹的冲击振动信号，计算最大冲击响应谱，将冲击响应谱相对峰值比、相对峰值频率比作为故障特征进行提取，并统计两个参数的分布特性，该分布特征可以有效地识别出故障类别的不同。

总之本文研究结果表明，基于冲击响应谱特征提取的新方法可以有效地揭示自动机的早期故障信息，是一种可以用于在线检测的新方法。

（References）

［1］ 薄玉成，王惠源.自动机结构设计［M］.北京:兵器工业出版社，2009:1-2. BO Yu-cheng，WANG Hui-yuan.Automatic mechanism construction design［M］.Beijing:Publishing House of Ordnance Industry，2009:1-2.（in Chinese）

［2］ 邹衍，徐诚，张克.5.8mm/7.62mm模块化步枪运动特性匹配分析［J］.兵工学报，2015，36（7）:1356-1362. ZOU Yan，XU Cheng，ZHANG Ke.Analysis of kinetic characteristic matching of 5.8 mm/7.62 mm modularized rifles［J］.Acta Armamentarii，2015，36（7）:1356-1362.（in Chinese）

［3］ 武春林，潘宏侠.火炮自动机故障诊断研究综述［J］.机械管理开发，2013（1）:115-116. WU Chun-lin，Pan Hong-xia.Research artillery automatic machine fault diagnosis［J］.Mechanical Management and Development，2013（1）:115-116.（in Chinese）

［4］ 熊超，吕建刚，张进秋，等.火炮身管超声波检测技术［J］.无损检测，2003，25（2）:102-104，107. XIONG Chao，LYU Jian-gang，ZHANG Jin-qiu，et al.Ultrasonic inspection of cannon［J］.Nondestructive Testing，2003，25（2）: 102-104，107.（in Chinese）

［5］ 车俊铁，侯强，于静.兵器零部件微裂纹检测方法的对比分析［J］.兵器材料科学与工程，2005，28（5）:44-47. CHE Jun-tie，HOU Qiang，YU Jing.Contrast analysis of testing methods for tiny crack in parts of weapon［J］.Weapon of Materials Science and Engineering，2005，28（5）:44-47.（in Chinese）

［6］ 潘保青，王坚，张洪伟.基于漏磁原理的火炮零部件裂纹检测装置的设计与实现［J］.测试技术学报，2010，24（6）: 552-557. PAN Bao-qing，WANG Jian，ZHANG Hong-wei.Design and implementation of flaw testing device based on magnetic flux leakage detect for gun components［J］.Journal of Testing Technology，2010，24（6）:552-557.（in Chinese）

［7］ 李辉，郑海起，唐力伟.Teager-Huang变换在齿轮裂纹故障诊断中的应用［J］.振动、测试与诊断，2010，30（1）:1-5，94. LI Hui，ZHENG Hai-qi，TANG Li-wei.Application of Teager-Huang transform to crack fault diagnosis of gear［J］.Journal of Vibration，Measurement＆amp;Diagnosis，2010，30（1）:1-5，94.（in Chinese）

［8］ 刘长利，夏春明，郑建荣，等.裂纹和油膜耦合故障转子周期运动分岔分析［J］.振动.测试与诊断，2008，28（1）:35-38，77. LIU Chang-li，XIA Chun-ming，ZHENG Jian-rong，et al.Study on bifurcation of periodic motion of rotor system with crack and oil whirl fault［J］.Journal of Vibration，Measurement＆amp;Diagnosis，2008，28（1）:35-38，77.（in Chinese）

［9］ Wang A Y，Pan H X，Liu H L.Study on fault feature extraction of high-speed automaton［J］.TELKOMNIKA Indonesian Journal of Electrical Engineering，2013，11（10）:5867-5875.

［10］ Wang A Y，Pan H X，Liu H L.Fault Diagnosis of automaton based on EMD and close degree［J］.Sensors＆amp;Transducers，2013，160（12）:612-618.

［11］ 潘宏侠，都衡，马春茂.局域波信息熵在高速自动机故障诊断中的应用［J］.振动.测试与诊断，2015，35（6）:1159-1164，1205.PAN Hong-xia，DU Heng，MA Chun-mao.High-speed automaton fault diagnosis based on local wave and information entropy［J］.Journal of Vibration，Measurement＆amp;Diagnosis，2015，35（6）:1159-1164，1205.（in Chinese）

［12］ 潘宏侠，兰海龙，任海峰.基于局域波降噪和双谱分析的自动机故障诊断研究［J］.兵工学报，2014，35（7）:1077-1082. PAN Hong-xia，LAN Hai-long，REN Hai-feng.Fault diagnosis for automata based on local wave noise reduction and bispectral analysis［J］.Acta Armamentarii，2014，35（7）:1077-1082.（in Chinese）

［13］ 李蓓蓓.基于现场跟踪记录的流通环境跌落冲击分析［J］.包装工程，2015，36（11）:83-86. LI Bei-bei.Analysis of drop and shock in circulation environment based on shock and vibration recorder［J］.Packaging Engineering，2015，36（11）:83-86.（in Chinese）

［14］ 董龙雷，张静静，赵建平.基于冲击响应谱的高速火箭橇滑轨路谱分析［J］.西南交通大学学报，2015，50（6）:1170-1174. DONG Long-lei，ZHANG Jing-jing，ZHAO Jian-ping.Road spectrum analysis of high-speed rocket sled rail based on shock response spectrum［J］.Journal of Southwest Jiaotong University， 2015，50（6）:1170-1174.（in Chinese）

［15］ 雷晓波，张强，张永峰.固定翼飞机外挂物着陆冲击响应谱研究［J］.飞行力学，2015，33（2）:161-164. LEI Xiao-bo，ZHANG Qiang，ZHANG Yong-feng.Research on shock response spectrum for fixed-wing aircraft landing with external store［J］.Flight Dynamics，2015，33（2）:161-164.（in Chinese）

［16］ Wright C.Effective data validation methodology for pyrotechnic shock testing［J］.Journal of the IEST，2010，53（1）:9-30.

［17］ Cordes JA，Vo P，Lee JR，et al.Comparison of shock response spectrum for different gun tests［J］.Shock and Vibration，2013，20（3）:481-491.

［18］ 华师韩，田恒春.冲击响应谱计算相关参数选择的研究［J］.遥测遥控，2005，26（6）:50-55. HUA Shi-han，TIAN Heng-chun.Consideration of the parameters choice for shock response spectrum evaluation［J］.Telemetry and Telecontrol，2005，26（6）:50-55.（in Chinese）

［19］ Smallwood DO.Improved recursive formula for calculating shock response spectra［C］∥1980 Shock and Vibration Symposium. San Diego，CA，US:NASA，1980.

［20］ Christian L.Mechanical shock［M］.Hoboken，NJ，US:John Wiley＆amp;Sons Ltd，2014:103-173.

Crack Fault Diagnosis of Automatic Mechanism Based on Shock Response Spectrum Features Extraction

LI Hai-guang1，2，PAN Hong-xia1，REN Hai-feng1
（1.College of Mechatronic Engineering，North University of China，Taiyuan，030051，Shanxi，China；2.Inner Mongolia Key Laboratory for Utilization of Bayan Obo Multi-Metallic Resources，Inner Mongolia University of Science and Technology，Baotou 014010，Inner Mongolia，China）

A new crack fault diagnosis method is presented for the automatic mechanism of high-speed gun.The method uses shock response spectrum（SRS）for features extraction.Impact vibration data are acquired in the weapon firing test in which different cracked parts are used.These data are separated according to gun operation status.The shock response spectra of the separated data are computed.Two new definitions of relative peak ratio and relative peak frequency ratio of response spectrum are proposed based on different response characteristics of response spectrum area.The relative peak ratio and relative peak frequency ratio as fault features are extracted.The various faults are recognized by comparing the Statistical distribution pattern of fault characteristic values under different crack conditions.The experimental result shows the proposed method can be used effectively and accurately to diagnose the crack failures ofgun automatic mechanism and is particularly applicable for on-line monitoring.

ordnance science and technology；fault diagnosis；operation status；shock response spectrum；relative peak ratio；relative peak frequency ratio

TJ06

A

1000-1093（2016）09-1744-09

10.3969/j.issn.1000-1093.2016.09.027

2016-03-21

国家自然科学基金项目（51675491）

李海广（1975—），男，副教授。E-mail:btlhgboy@163.com；潘宏侠（1950—），男，教授。E-mail:panhx1015@163.com