高精度狙击步枪弹与枪匹配设计方法研究

刘国庆，徐诚

（南京理工大学机械工程学院，江苏南京210094）

高精度狙击步枪弹与枪匹配设计方法研究

刘国庆，徐诚

（南京理工大学机械工程学院，江苏南京210094）

为了研究狙击步枪弹与枪匹配设计方法，基于非线性有限元理论建立了弹与枪相互作用数值计算模型，该模型是一个较为完善的求解弹头膛内发射过程的计算模型，通过对比试验结果与仿真结果证明了该模型的正确性。将稳健设计思想应用于弹与枪匹配设计，选取多个弹、枪设计参数作为控制因素，弹头质量偏心为噪声因素，弹头膛内摆动角为性能度量，采用正交试验法开展稳健性研究，获得了各参数在两水平值处的稳健特性；正交试验所得4组枪、弹参数匹配组合方案在有无噪声状态下的方案优劣结果与精度射击试验方案结果基本一致，证明了将稳健设计思想应用于弹与枪匹配设计的可行性、正确性。

兵器科学与技术；狙击步枪；匹配设计；数值模型；耦合计算；稳健设计

0　引言

高精度狙击步枪是一种具有较高加工精度、高射击精度的身管武器，在工程实践中存在特有的结构匹配现象，即不同结构参数的弹与枪管相互组合射击时能够获得不同的射击精度，如果能够揭示狙击步枪弹与枪在结构方面匹配上的机理，寻求一种可行的匹配设计方法，将对提高狙击步枪射击精度具有重要实际意义。目前狙击步枪弹与枪结构匹配的机理尚不完全清楚，相关工程实践与理论方面的研究报道较少，国内外针对弹与枪结构匹配现象缺乏系统的研究方法，成为阻碍进一步提高狙击步枪射击精度的瓶颈。

进行弹与枪匹配设计的目的是寻找一组或几组参数的组合，参数组合能够在各种不可控因素的干扰下使得狙击步枪仍然具有较高的射击精度，这与稳健设计方法的思想十分相似，因此可将稳健设计思想应用于弹与枪匹配设计方法之中。稳健设计方法在武器系统研究中已开展应用，如赵旅［1］应用稳健设计方法获得了炮尾炮闩结构在多质量指标下的稳健设计方案；陈建江［2］在稳健设计理论的基础之上，提出了一种基于正交试验的稳健优化设计方法，获得了飞航导弹系统的稳健最优解；孙鹏［3］将多质量特性指标的稳健设计思想应用于固体火箭发动机的结构设计中，部件满足了设计要求与设计目标，同时还将发动机结构性能对各噪声因素的敏感性降至最小，获得了高稳健性的设计参数。

本文采用正交试验法对弹、枪主要设计参数开展参数匹配研究，正交试验以弹与枪相互作用数值计算模型为仿真平台，进行噪声因素干扰下的参数组合稳健特性分析工作，依据参数组合状态加工枪、弹，开展精度射击试验验证正交仿真实验所得稳健分析结果。

1　弹与枪相互作用有限元数值计算模型

1.1三维建模与网格划分

依据枪管、狙击弹结构参数分别建立三维模型，使用有限元前处理软件划分网格，其网格模型如图1、图2所示。网格类型以六面体缩减积分实体单元为主（C3D8R），其中枪管共划分267 529个网格，弹头壳共划分175 769个网格，铅芯共划分110 868个网格。

图1　枪管半剖网格模型Fig.1 Half sectional mesh model of barrel

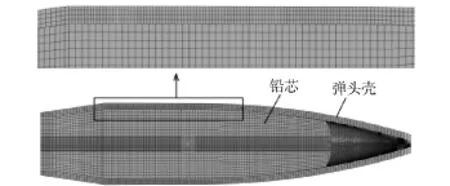
图2　弹丸半剖网格模型Fig.2 Half sectional mesh model of bullet

装配时，弹头处于坡膛前部，与实际装配位置一致，由有限元计算程序计算弹头挤进与膛内运动过程。

1.2显隐式混合运算

模型考虑了重力作用导致的枪管预弯曲现象，在处理该问题时首先使用隐式求解器获得枪管在重力作用下的应力、应变状态，而后将隐式计算结果导入显式求解器，重新设置约束状态、接触性质与初始场等计算初始条件，求解弹头发射过程，经混合运算获得重力导致的枪管弯曲对弹头膛内发射过程的影响［4］。

1.3内弹道计算与ABAQUS数值计算耦合的实现

基于经典内弹道方程组，使用Fortran语言编写了内弹道计算程序。内弹道计算与ABAQUS弹头发射过程数值计算相耦合，以膛压与弹头位移为中间传递量，充分考虑膛压生成与弹头运动之间的耦合关系［5］，耦合计算流程图如图3所示。

图3　耦合计算流程图Fig.3 Flow chart of coupling calculation

2　模型的验证

采用铜柱测压法进行了膛压测试试验，采用光电法进行了初速测试试验，采用高速摄影法进行了枪口振动测试试验，试验结果与仿真结果对比如表1与图4所示，其中v0、pm、f、Amax与η分别为初速、膛压、枪口振动频率、最大幅值与衰减系数。对比数据表明计算结果与试验结果一致性较高，证明了模型的正确性。

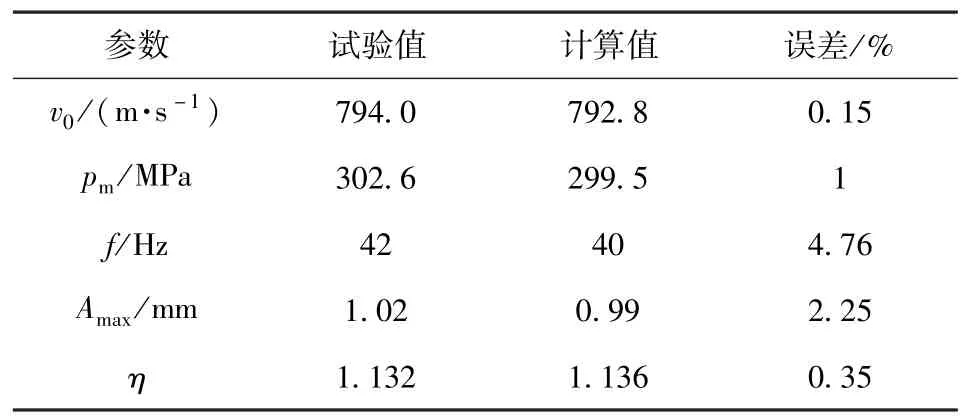
表1　数据对比表Tab.1 Data comparison table

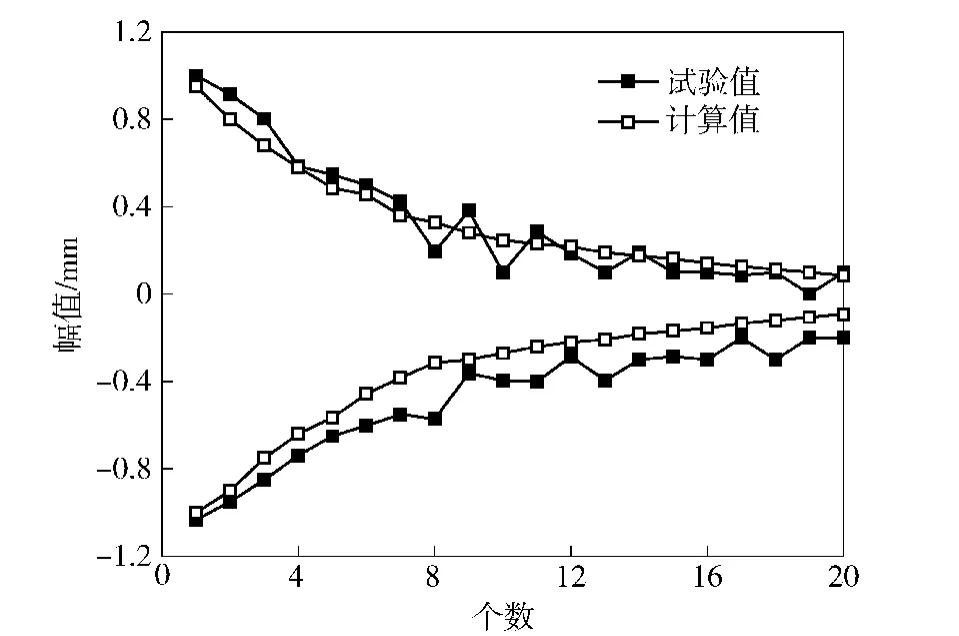
图4　枪口振动衰减曲线Fig.4 Attenuation curves of muzzle vibration

3　匹配设计

狙击步枪弹与枪匹配设计的目的是寻求一组或多组稳健性好的参数组合，这与稳健设计方法的思想相同，因此可将稳健设计思想应用于弹与枪匹配设计。稳健设计的一般步骤如下［6-8］:1）确定控制因素、噪声因素与性能度量；2）规划试验计划；3）实施试验；4）试验结果分析。其中，试验通常以正交试验表的方式进行规划。

3.1因素确定与性能度量

控制因素包含枪、弹所有可控设计参数，控制因素的选取需要根据其对性能度量的影响程度确定；噪声因素为不可控影响因素，通常不可控因素作为噪声因素进行考虑；性能度量也可称为目标函数，反映各种因素变化对系统的影响情况。对于狙击步枪而言，弹头膛内摆动角最大值与射击精度优劣密切相关，因而可将弹头膛内摆动角最大值作为性能度量。

在枪、弹主要设计参数范围内均匀地选取5个参数值，观察参数值变化对性能度量的影响程度，以弹与枪相互作用数值模型为平台所得计算结果如表2所示，表2中相对变化率表示因参数值变化导致的摆动角平均差相对于参考值的变化大小。为了更好地体现匹配性，从枪、弹设计参数中各选取3个参数进行后续匹配工作，选取原则为依照参数对性能度量的影响大小进行取舍，得到6个设计参数作为控制因素，如表3所示。

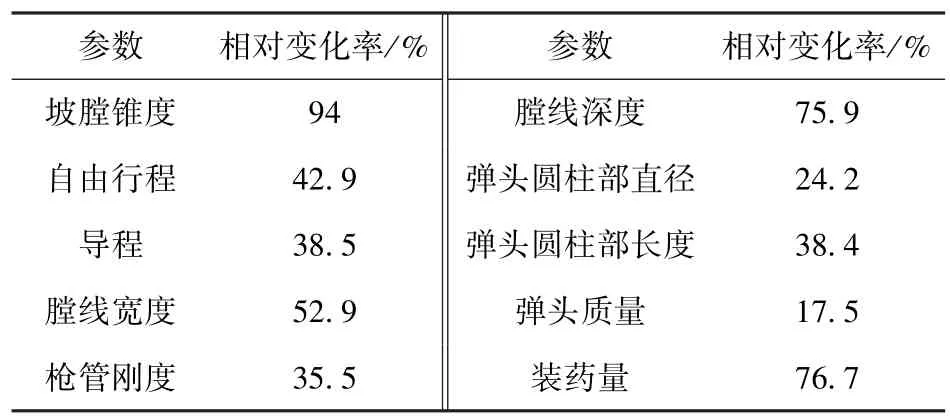
表2　参数影响情况表Tab.2 Effects of parameters on performance measure

表3　参数表Tab.3 Parameter list

弹丸质量偏心对弹头膛内摆动角的影响远高于其他因素，是影响射击精度的最重要因素［9-10］，因此将弹丸偏心量作为噪声因素。

3.2因素水平表与正交表

3.2.1因素水平的选取

本文对每个控制因素选取两个水平值进行分析，因素水平值的选取依据参数设计的非线性效应，要求水平值所形成的参数区间使得性能度量均值与极差均最小，最优水平值在上述参数范围内而不限于上述5个水平值。控制因素在多个水平值处对性能度量的影响情况如图5、图6所示。控制因素水平值如表4所示，其中A表示坡膛锥度，数字1，2，…，5表示坡膛锥度的不同取值，其他字母与数字含义依次类推。

图5　枪管参数对性能度量的影响Fig.5 Effect of barrel parameter on performance measure

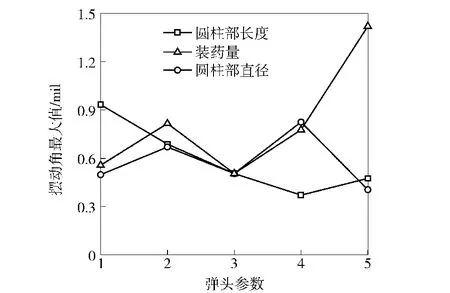
图6　弹头参数对性能度量的影响Fig.6 Effect of bullet parameter on performance measure

表4　因素水平值Tab.4 Level values of control factors

如图5所示，坡膛锥度与膛线深度两因素对性能度量的影响近似呈现“U”型，当坡膛锥度为1.5°、膛线深度为0.095mm时性能度量值最小，依据非线性效应，坡膛锥度的两个最优水平值为1.5°与2°，膛线深度的两个最优水平值为0.085mm与0.095mm；性能度量值随着膛线宽度的增大而增大，因此膛线宽度的两个最优水平值为1.73mm与1.83mm.

如图6所示，随着弹头圆柱部长度增加，性能度量呈现先减小、后增大的趋势，当圆柱部长度为9.5mm时性能度量值最小，最优水平值为9 mm与10mm；圆柱部直径与装药量对性能度量的影响并未呈现明显的趋势，圆柱部直径为7.92 mm时性能度量值最小，但最优水平值却为7.84 mm与7.87mm，二者所形成的参数区间使得性能度量的均值与极差最小；装药量为3.45 g时性能度量值最小，最优水平值为3.4 g与3.5 g.控制因素两个水平值如表5所示，噪声因素Z同样选取两个水平值，即0.025mm与0.05mm.

表5　因素两水平值Tab.5 Twolevel values of control factors

3.2.2正交表

为充分考虑噪声因素的影响，本文将噪声因素作为控制因素，采用L8（27）正交表进行试验规划，如表6所示，字母与数字含义同上所述。

表6　正交表Tab.6 Orthogonal table

3.3正交试验结果与分析

依照L8（27）正交表的规划，分别进行8次数值仿真实验，所得性能度量值结果如图7所示，其中Z1与Z2所示曲线分别表示在质量偏心为0.025 mm与0.05mm情况下的4次仿真实验结果。

对正交仿真实验结果进行均值与极差分析，均值图与极差图如图8所示，数据点表示该水平值处的均值，竖线长度表示该水平值处的极差大小，A1均值的含义为所有包含水平值A1的试验结果（如θ1、θ2等）的平均值，A1极差RA1的含义为所有试验结果的最大差值，如（1）式、（2）式所示，其他因素均值、极差的含义与此相同。

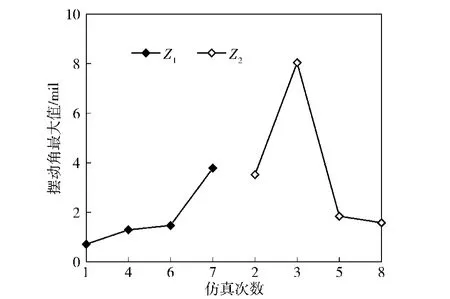
图7　性能度量值Fig.7 Performance measures

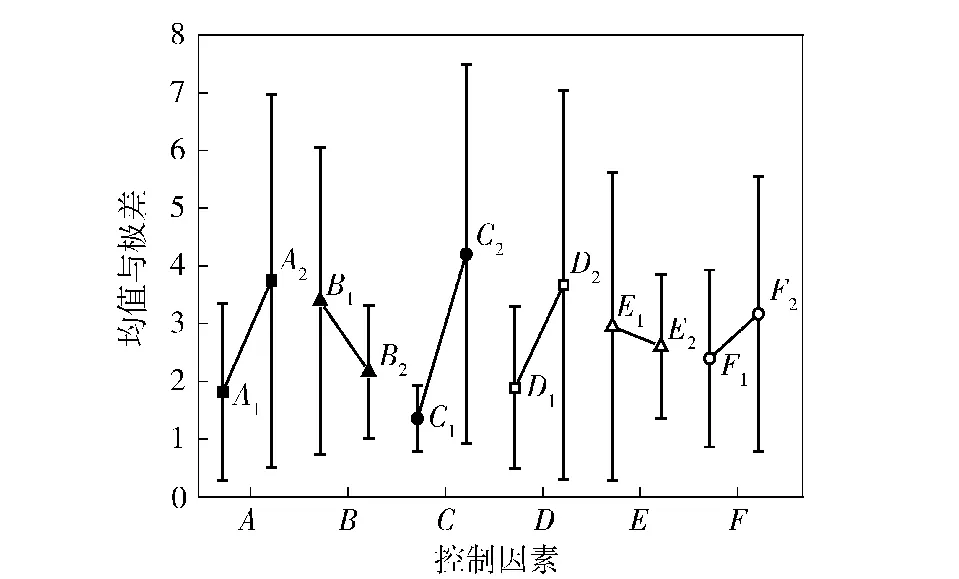
图8　均值与极差Fig.8 Mean value and range

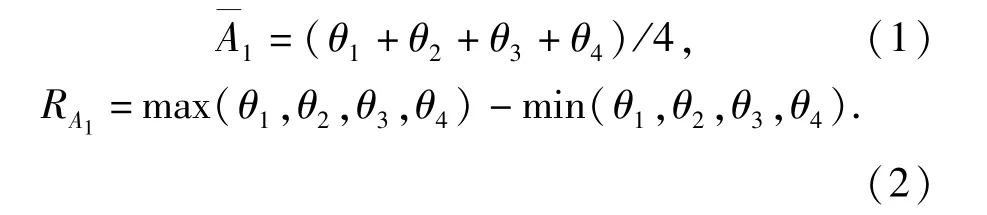
由图8可知，控制因素A在水平值A1处的摆动角均值与极差均小于水平值A2，均值与极差分别相对降低了约51.6％和52.5％，因此水平值A1是控制因素A的最优值；水平值B2、C1、D1、E2与F1具有均值小与极差小的特点，因此是其他控制因素的最优值。

4　稳健特性验证

4.1参数组合

经过均值与极差分析，参数组合Ⅰ（A1，B2，C1，D1，E2，F1）具有均值小与极差小的稳健性，为了验证参数组合的稳健性分析结果，本文将分析3种参数组合在多组噪声因素状态下的计算结果是否与稳健分析结果一致。参数组合Ⅱ（A2，B1，C2，D2，E1，F2）与组合Ⅰ的取值相反，组合Ⅲ（A1，B2，C1，D2，E1，F2）为组合Ⅰ前半部分与组合Ⅱ后半部分组合。

4.2噪声因素

弹头质量偏心是影响弹头膛内摆动的最大因素，若参数组合在弹头偏心状态下具有良好的稳健性，则可以认为该参数组合在其他干扰因素影响下依然具有良好的稳健性；本节将考虑在无噪声与4组噪声状态下性能度量值的变化规律，弹头偏心距分别为0.025 mm、0.050 mm、0.075 mm与0.100mm.

4.3计算结果与分析

有无噪声状态下的性能度量值变化规律如图9所示，参数组合Ⅰ、Ⅱ与Ⅲ在有无噪声状态下的性能度量值均比原始参数小，即3种参数组合状态均优于原始参数状态，表明将参数的最优水平值进行组合能够起到降低性能度量值的作用。4种参数状态下的性能度量值如表7所示。

图9　摆动角最大值变化规律Fig.9 Change rule of maximum swing angles

表7　摆动角最大值Tab.7 Maximum swing angles mil

参数组合Ⅰ的均值与极差最小，相对于原始参数组合与参数组合Ⅱ、Ⅲ，均值分别低41.7％、27.5％与13.4％，极差分别低43.3％、24.6％与6.3％，组合Ⅰ在总体上优于另外3种参数组合，表明正交试验所得参数稳健特性结果是正确的。

4种参数组合在无噪声状态下的性能度量值相差无几，而随着质量偏心距的增大，彼此之间的性能度量差值越来越大，表明噪声因素越大则参数组合Ⅰ的稳健性体现得越好，如图10～图12所示4组参数组合在偏心距为0mm、0.050mm与0.100 mm时的弹头膛内摆动角曲线，原始参数组合与参数组合Ⅰ之间的最大摆动角差值分别为0.13 mil、1.77mil与3.52 mil.此外，3种参数组合中组合Ⅰ最优，组合Ⅲ次之，组合Ⅱ最差，组合优劣与3种组合中的参数最优值数目相关，表明最优值越多则参数组合的稳健性越好。

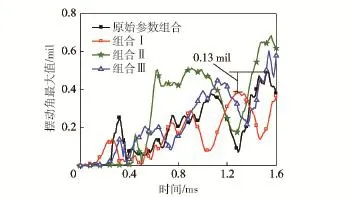
图10　摆动角曲线（弹头质量偏心量0mm）Fig.10 Curves of swing angle with eccentricity of 0mm

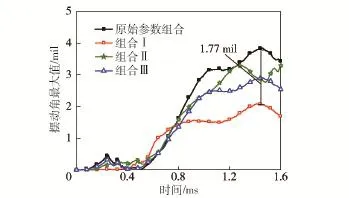
图11　摆动角曲线（弹头质量偏心量0.050mm）Fig.11 Curves of swing angle with eccentricity of0.050mm

图12　摆动角曲线（弹头质量偏心量0.100mm）Fig.12 Curves of swing angle with eccentricity of0.100mm

4.4试验验证

为了验证参数组合Ⅰ与参数组合Ⅱ的稳健性能，分别加工两种参数状态下的狙击步枪枪管，并选配了高精度枪弹，如图13、图14所示，通过试验验证原始参数组合、参数组合Ⅰ与参数组合Ⅱ的射击精度。

图13　3种参数组合状态下的枪管Fig.13 Three barrels with different parameter combination

图14　3种参数组合状态下的弹Fig.14 Three bullets with different parameter combination

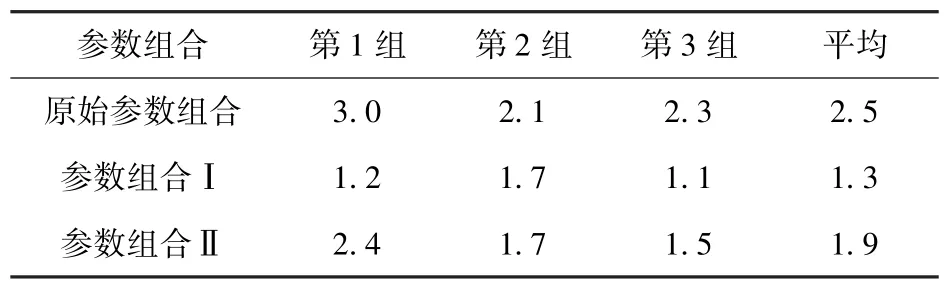
表8　散布圆直径Tab.8 Diameter of scattered circle cm

对3种参数组合状态下的枪、弹进行精度射击试验，每种参数组合状态下进行3组射击试验，每组射击试验射击3发弹，记录3发弹的最大散布圆直径，试验结果如表8所示。精度射击试验结果表明，参数组合Ⅰ状态下的射击精度最高，参数组合Ⅱ次之，原始参数组合状态最差，与正交仿真实验结果及有无噪声状态下的计算结果均一致，证明了将稳健设计思想应用于弹与枪匹配设计方法的可行性与正确性。

5　结论

本文为了研究狙击步枪弹与枪匹配设计方法，建立了弹与枪相互作用计算模型，并通过试验验证了计算模型的正确性；将稳健设计思想应用于弹与枪匹配设计，获得了弹与枪主要参数在两水平值处的稳健特性，并对稳健特性分析结果进行了验证，归纳全文共有以下5点结论:

1）弹与枪相互作用计算模型综合考虑了挤进作用、重力导致的枪管预弯曲及火药燃烧与弹头运动的耦合作用，是一个较为完善的弹头膛内发射过程求解模型，通过对比计算结果与试验结果证明了该模型的正确性。

2）选取弹、枪多个设计参数作为控制因素，弹头质量偏心为噪声因素，弹头膛内摆动角为性能度量，采用正交试验法规划了仿真实验，获得了各参数水平值的稳健特性；分析了4种参数组合在有无噪声状态下的性能度量值，计算结果显式各参数组合的稳健特性与正交试验结果一致。

3）有无噪声状态下参数组合Ⅰ、Ⅱ、Ⅲ计算所得性能度量值优于原始参数，表明将参数分析所得最优水平值相组合能够起到降低性能度量值的作用，但组合的稳健性能与参数组合所具有的参数最优值数目相关。

4）3种参数组合在无噪声状态下的性能度量值相差较小，但随着噪声因素的增大，彼此之间的性能度量差值逐渐增大，即噪声因素越明显则参数组合的稳健性能体现得越好。

5）依据参数组合Ⅰ与参数组合Ⅱ加工并匹配枪、弹，通过与原始参数状态下的枪、弹射击精度的对比发现，3种参数组合状态下的精度试验最优方案与匹配设计最优方案基本一致，从试验角度证明了将稳健设计思想应用于弹与枪匹配设计方法的可行性、正确性。

（References）

［1］ 赵旅.炮尾炮闩结构的多目标优化及稳健设计［D］.南京:南京理工大学，2008. ZHAO Lyu.Multi-objective optimization and robust design of cannon tail and bolt structure［D］.Nanjing:Nanjing University of Science and Technology，2008.（in Chinese）

［2］ 陈建江.面向飞航导弹的多学科稳健优化设计方法及应用［D］.武汉:华中科技大学，2004. CHEN Jian-jiang.Method and application of winged missile oriented multidisciplinary robust design optimization［D］.Wuhan:Huazhong University of Science and Technology，2004.（in Chinese）

［3］ 孙鹏.稳健设计方法及其在火箭发动机结构设计中的应用［D］.西安:西北工业大学，2006. SUN Peng.Robust design method and its application in rocket engine structure design［D］.Xi'an:Northwestern Polytechnical U-niversity，2006.（in Chinese）

［4］ 林秉奇.基于弹炮耦合的火炮非线性动态特性分析与研究［D］.南京:南京理工大学，2013. LIN Bing-qi.The nonlinear dynamic character study and analysis of artillery based on projectile-barrel coupling system［D］.Nanjing:Nanjing University of Science and Technology，2013.（in Chinese）

［5］ 丁传俊，张相炎.基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究［J］.兵工学报，2015，36（12）:2254-2261. DING Chuan-jun，ZHANG Xiang-yan.Simulation study of bearing band engraving process and interior ballistic Process based on thermo-mechanical coupling FEA model［J］.Acta Armamentarii，2015，36（12）:2254-2261.（in Chinese）

［6］ Taguchi G，Jugulum R.The Mahalanobis-Taguchi strategy:a pattern technology system［M］.US:John Wiley and Sons，1988.

［7］ Mike P.Design of experiments［M］.US:Createspace，2013.

［8］ Ulrich K T，Eppinger SD.Product design and development［M］. Italy:McGraw-Hill Education，2011.

［9］ Liu G Q，Xu C.Impact study ofmass eccentricity of sniper rifle bullet on initial disturbance［C］∥4th International Conference on Advanced Engineering Materials and Technology.Xiamen，China: ICAE，2014.

［10］ 李强.影响弹丸起始扰动的某火炮结构参数分析与优化研究［D］.南京:南京理工大学，2015. LIQiang.Analysis and optimization research of gun structure parameters affecting initial projectile disturbance［D］.Nanjing: Nanjing University of Science and Technology，2015.（in Chinese）

The Study of Bullet-Barrel Matching Design Method of High Precision Sniper Rifle

LIU Guo-qing，XU Cheng
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

A numerical calculation model of interaction between bullet and barrel is established to deeply study a matching design method of sniper rifle，which is based on nonlinear finite element theory.The proposed model is a comprehensive theory model to analyze launch process.Validation experiments were conducted.The experimental results are in agreement with the calculated results.The orthogonal experimental method is used to study the robustness of the main design parameters of bullet and barrel，in which the design parameters of bullet and barrel，the eccentric mass of bullet and the swing angle are taken as control factors，noise factor and performance measure，respectively.The calculated results of design parameter robustness in two levels are obtained.The calculated results of four groups of matching parameters of barrel and bullet with or without noise factor are agreed with the experimental results，which proves the correctness and feasibility of the robust design for matching design of bullet and barrel.

ordnance science and technology；sniper rifle；matching design；numerical model；coupling calculation；robust design

TJ202

A

1000-1093（2016）09-1592-07

10.3969/j.issn.1000-1093.2016.09.006

2016-03-07

国家自然科学基金项目（51575279）

刘国庆（1988—），男，博士研究生。E-mail:guoqingcool@126.com；徐诚（1962—），男，教授，博士生导师。E-mail:xucheng62@mail.njust.edu.cn