减振系统造成捷联惯性导航误差的有限元分析方法

高军强，汤霞清，黄湘远，程旭维

（装甲兵工程学院控制工程系，北京100072）

减振系统造成捷联惯性导航误差的有限元分析方法

高军强，汤霞清，黄湘远，程旭维

（装甲兵工程学院控制工程系，北京100072）

为研究减振系统由于破坏捷联惯性导航与载体之间固联关系而造成的惯性导航测量误差，分析误差机理，提出一种基于有限元的分析方法。在有限元软件中建立带减振器的捷联惯性导航系统模型，利用轨迹发生器生成的运动参数，对载体及惯性导航系统运动过程进行仿真。仿真结束后，从有限元分析结果中提取惯性器件测量数据，经导航解算，得到减振系统造成的惯性导航误差。研究结果表明，有限元分析方法能够实现减振系统造成惯性导航误差的定量分析，使得可以从捷联惯性导航测量精度的角度进行减振系统优化设计。

兵器科学与技术；捷联惯性导航系统；减振系统；误差；有限元分析

0　引言

捷联惯性导航系统是目前武器装备上广泛应用的精密测量仪器，它将惯性导航设备与运动载体直接固联，精确测量载体位置、姿态等信息，为实现超视距精确打击、协同作战等战术意图提供必要条件。但是，载体在运动过程中往往存在各种振动、冲击激励，如果直接作用在惯性器件上会对其测量精度造成不良影响［1-2］。因此，实际应用中通常需要进行减振设计，改善惯性器件的工作环境［3］。减振器作为一种弹性元件，在运动过程中会发生形变，实际上破坏了惯性导航系统与载体之间的固联关系，引入了新的系统误差源。捷联惯性导航系统作为精密测量仪器，测量精度是关键性指标，如何保证减振系统在有效隔离振动、冲击激励的同时，不对惯性导航精度产生负面影响至关重要。

减振系统设计是惯性导航系统实用化过程中的关键技术之一。在设计过程中通过建立系统动力学模型，采用数值仿真的方法，可以对振动、冲击隔离效果进行分析［4-5］，是进行隔冲减振系统设计的重要理论基础。但在建立实际系统动力学模型时需要进行较大的简化，会对分析结果的精确性造成一定影响。利用有限元方法，结合实际测试实验，建立精确的惯性导航及减振系统有限元模型，通过有限元动力学分析可以得到更精确的动态响应，在解决实际问题方面更为有效［6-7］。

为保证测量精度，惯性导航系统对减振系统的特殊要求主要体现在两个方面:一是实现各自由度运动通道的振动解耦，理论上需要隔冲减振系统弹性中心与惯性导航系统质心重合，但实际系统中，偏心现象往往无法避免，实现完全解耦几乎是不可能的；二是尽量提高角振动与线振动频率比值，但这种方法只是对角振动具有一定抑制作用，并不能完全消除［8］。总之，为惯性导航系统设计的减振系统既要有效隔离线振动，又不能产生附加的角振动，即需要无角位移减振装置，此类装置已经有一定研究［9］，但是还不能实现角振动的完全消除。

在惯性导航系统结构设计，尤其是减振系统设计方面，有限元方法已经被广泛采用，但是目前主要用于对惯性导航系统结构动力学特性进行研究，并没有直接从惯性导航精度的角度进行分析。对于精度能否满足使用要求，通常是完成样机生产之后，开展验证实验［10］，这就极大降低了设计效率。针对减振系统会造成惯性导航测量误差的现实问题，提出基于有限元的仿真分析方法，可以对各种情况进行分析，便于从惯性导航测量精度的角度实现系统结构优化设计，使设计过程更加高效。

1　减振系统造成捷联惯性导航误差机理分析

减振器变形是减振系统造成捷联惯性导航测量误差的直观原因，而具体如何产生影响，有必要进行深入分析。首先对涉及到的坐标系符号进行说明:地心惯性坐标系i；地球坐标系e；地理坐标系（东—北—天）即导航坐标系n；载体坐标系（右—前—上）b；惯性导航系统坐标系s.

根据惯性导航工作原理，加速度计和陀螺的测量值分别是惯性导航系统相对于i系运动的比力和角速度在s系下的投影，即捷联惯性导航系统与载体之间是固联关系，则二者在i系下的运动完全一致，即

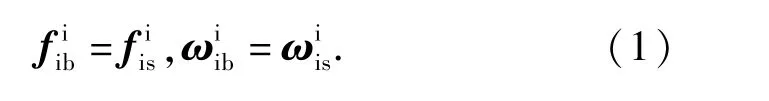
又因为在理想安装条件下，s系与b系的指向一致，s系下的投影与b系下的投影相同，即

显然，由（1）式和（2）式可以推得

（3）式说明，捷联惯性导航中加速度计和陀螺的测量值就是载体相对于i系运动的比力和角速度在b系下的投影，因此，经过导航解算便实现了载体姿态、位置的精确测量。

然而，如图1所示加入减振器之后的捷联惯性导航系统，减振器在运动过程中产生变形，导致惯性导航系统与载体之间存在相对运动，使（1）式不成立；惯性导航系统相对于载体发生转动，使s系与b系坐标轴指向不再一致，（2）式也不成立。最终导致（3）式不能成立，惯性导航系统不能实现载体运动参数的精确测量，引入了系统测量误差。

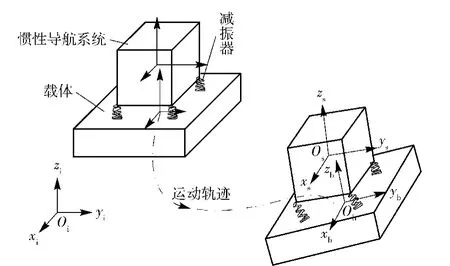
图1　带减振器的捷联惯性导航系统示意图Fig.1 SINS model with vibration isolation system

进一步分析，令Δfb、Δwb分别代表惯性导航系统与载体之间由于减振器变形所产生的相对线运动和相对角运动在b系下的投影，则

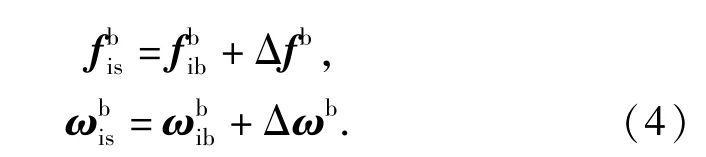
减振器变形造成的载体运动参数测量误差可以表示为

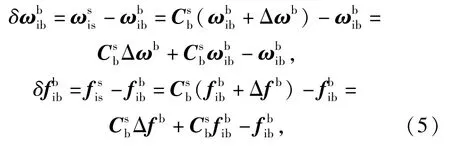
式中:对于任意坐标系α、β，Cβα表示由α系到β系的转换矩阵。

若惯性导航系统与载体之间不存在相对角运动，即Δwb=0，则

若惯性导航系统与载体之间不存在相对线运动，即Δfb=0，则

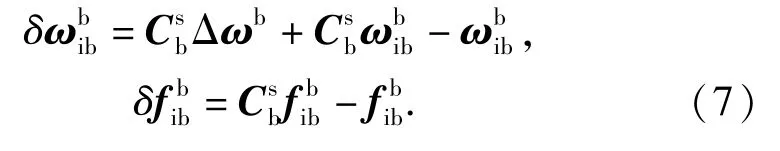
由（6）式、（7）式可以很直观地看出，相对角运动对测量精度的影响要远远超过相对线运动所产生的影响，因此，在惯性导航系统减振设计中抑制惯性导航系统与载体之间的相对转动至关重要。

以上对减振系统造成捷联惯性导航测量误差的机理进行了定性分析，明确了Δfb、Δwb对测量精度的影响情况。在进行定量研究时，如果从误差源出发，需要对减振器变形量进行测量以确定Δfb、Δwb，且减振器变形量的实时测量，也可以用于进行误差补偿，但是实际中较难实现。一个更直观的定量研究方法是获取真实的数据，这可以通过在载体上同时安装一套带减振器的惯性导航系统和一套不带减振器的惯性导航系统进行实际测量，也可以使用动力学软件仿真实现，而仿真方法明显可以节省大量人力、物力，达到事半功倍的效果。

2　系统有限元模型

为了采用有限元方法分析减振系统造成的导航误差，首先对惯性导航系统8个角上安装减振器的结构建立有限元模型。相对于减振器而言，惯性导航系统和载体的刚度非常大，可以看作刚体，而且进行有限元分析的目的是获得惯性导航系统和载体的运动参数，并不关注机械结构内部力的变化。因此，在建立系统有限元模型时，将惯性导航系统设置为集中质量点，质量为6 kg，相对于s系3个轴的转动惯量相同，为0.08 kg·m2，而载体的质量、转动惯量等参数对分析过程不造成任何影响，只需要设置一个参考点，用于定义其运动参数即可。

对于减振器建模，采用ABAQUS软件自带的Bushing连接单元模拟弹性阻尼连接，这是目前普遍采用的减振器简化有限元模型，其三向线刚度相同，为3×104N/m，三向角刚度相同，为600 N·m/（°），阻尼为0.15.

如图2所示为建立的有限元模型，RP-1～RP-12是惯性导航系统上的参考点，定义为刚体约束；RP-1位于惯性导航系统质心处，设置集中质量点，对惯性导航系统质量、转动惯量进行定义；RP-2～RP-4用于在有限元分析结果后处理中建立s系。RP-13～RP-24是载体上的参考点，定义为刚体约束；RP-13位于载体质心处，用于定义载体运动参数；RP-14～RP-16用于在后处理中建立b系。8组参考点对:RP-5与RP-17，RP-6与RP-18，…，RP-12与RP-24之间定义Bushing连接，用于模拟减振器。

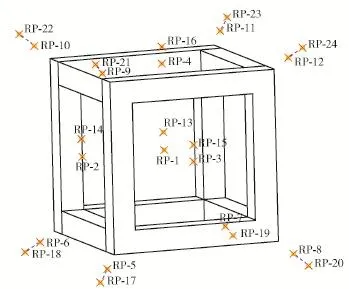
图2　带减振器的捷联惯性导航系统简化有限元模型Fig.2 A simplified finite element model of SINS with vibration isolation system

此外，有限元模型中，还建立了一个实体框架结构，其作用是辅助进行初始姿态的定义及后处理时获取重力加速度时程数据。在分析过程中，将该框架定义为密度为0的刚体，运动状态由RP-1控制，不会对分析过程及结果造成影响。

由于本文主要目的是对提出的方法进行验证，因此在建立有限元模型时做了比较大的简化。在解决实际问题时，减振器的非线性特性不容忽视，惯性导航系统有限元模型也需要根据相关实验进行反复修正，才可以做到精确模拟，这些方面已经有大量的研究可供参考［11-12］，本文不进行深入讨论。

3　基于有限元的分析方法

建立有限元模型之后，进行运动参数定义，运行动力学分析模拟载体及惯性导航系统的运动过程，分析结束后从结果文件中提取加速度、角速度数据作为惯性器件的测量值。由于整个有限元分析及结果提取过程中对惯性器件测量误差、初始对准误差等传统误差源进行了理想化处理，即不会产生任何误差，唯一造成惯性导航测量误差的就是减振系统变形。因此，将提取的运动数据作为惯性器件测量值进行导航解算，与真实的运动轨迹相比较，便可以实现减振系统变形造成惯性导航误差的定量分析，整体分析流程如图3所示。

图3　减振系统造成捷联惯性导航误差的有限元分析方法Fig.3 FEA method for SINS error caused by vibration isolation system

3.1生成运动参数

在惯性导航算法研究过程中，经常采用轨迹发生器仿真生成惯性器件测量数据，用于验证算法性能。本文通过对传统轨迹发生器进行改进，使其可以生成在有限元环境中模拟载体运动过程的加速度及角速度时程。

传统轨迹发生器生成的直接是惯性器件测量数据，即角速度与比力在b系下的投影。而在有限元软件中进行运动仿真时需要的是载体真实的运动参数:角速度与加速度，且有限元软件中不易实现相对于运动坐标系的运动参数定义，故应该将角速度与加速度投影至i系下。综上，需要对传统轨迹发生器进行两方面改进:1）将比力数据调整为加速度数据；2）将投影坐标系由b系转换为i系。

根据加速度计工作原理，传统轨迹发生器生成的比力在n系下表达式为

式中:an为载体运动的真实加速度，也就是有限元运动仿真时需要的真实加速度为载体相对地球转动产生的向心加速度为地球自转运动和载体相对地球的线运动互相影响形成的哥氏加速度；g为重力加速度。后面3项不是载体的真实运动，但却是加速度计测量值的一部分。因此，将后3项统称为有害加速度，记作在有限元分析过程中用于定义重力场，辅助提取加速度计测量数据。将真实加速度与有害加速度分离之后，便可以根据传统轨迹发生器得到真实加速度、有害加速度、角速度在b系下的投影。然后，利用b系到i系的转换矩阵即可将运动参数由b系投影至i系。

3.2设置动力学分析任务

设置动力学分析任务时，除定义载体运动过程外还有两项重点工作:1）将载体及惯性导航系统调整至仿真运动的初始状态；2）设置输出变量，用于提取惯性器件测量数据。

通常情况下，建立有限元模型之后，b系与i系的坐标轴指向是一致的，那么要使载体处于设定的初始姿态就要对模型进行旋转。为了简化旋转角度的计算，可以设定运动开始时e系与i系重合，b系与n系重合，即设置初始姿态角为［0°0°0°］.若设定载体的初始位置为纬度39°，经度118°，可以计算得到b系与i系指向一致时，载体的姿态角为俯仰43.328 412°，横滚30.102 975°，方位139.805 712°.根据姿态角的定义，为了使载体初始姿态角为［0°0°0°］，应该对系统有限元模型作如下旋转:

1）绕b系的y轴旋转-30.102 975°；

2）绕旋转后b系的x轴旋转-43.328 412°；

3）绕旋转后b系的z轴旋转-139.805 712°.此时b系便与n系重合，载体的姿态角为［0°0°0°］，满足了初始设定。

在动力学分析时，利用生成的角速度、加速度时程定义载体运动过程，有害加速度时程定义重力场。设置场变量输出，按固定的时间间隔输出整个模型的位移、速度、加速度以及重力数据。

3.3提取惯性器件测量数据

动力学分析任务运行结束后，对结果文件进行后处理，提取惯性器件测量数据是实现有限元分析与惯性导航仿真相结合的关键。由于惯性器件测量数据是角速度与加速度在s系下的投影，该坐标系是一个跟随惯性导航系统运动的动坐标系。然而，与运动参数输入时相同，有限元动力学分析结果中的运动参数也只能是在固定坐标系，即i系下的投影。因此，提取惯性器件测量数据的重点是在有限元软件中实现输出坐标系转换。

采用ABAQUS软件的Result Options选项卡，可以将有限元结果文件中包含的场变量输出数据转换到用户定义的任意坐标系下，此处选择目标坐标系为由RP-1～RP-4建立的s系。然后，从转换后的场变量输出数据中建立时程数据（即ABAQUS软件中的XY Data），选择节点RP-1，设定输出变量为3向加速度与3向角速度，即可得到RP-1在运动仿真过程中s系下的加速度与角速度时程，其中角速度时程便是陀螺仪输出数据。按照同样的方法，输出实体框架模型上任意点的重力加速度时程，也就是有害加速度时程，与加速度时程进行线性叠加即可得到加速度计输出数据，上述提取流程如图4所示。

图4　惯性器件测量数据提取流程Fig.4 Flow chart of measured data extraction

4　仿真分析

4.1仿真实验设计

为验证方法的有效性，采用图2建立的简化模型，在有限元软件中模拟了冲击实验过程。设置初始位置为纬度39°，经度118°，b系与n系重合，e系与i系重合，载体受到来自zb方向的如图5所示冲击加速度激励。在冲击作用开始前，载体及惯性导航系统处于静止状态，利用改进后的轨迹仿真方法生成冲击加速度激励相对应的加速度、角速度时程，对代表载体质心的参考点RP-13进行6自由度运动约束。则在整个冲击过程中，载体只在高度方向发生平移，经度、纬度保持不变，姿态角保持为0°.有限元分析结束后从结果文件中提取RP-1、RP-13的运动数据开展后续研究。

为研究角振动与线振动存在耦合时，减振器变形引入的系统测量误差，在载体运动过程设置相同的情况下，分别设计了惯性导航系统质心相对于减振系统弹性中心沿xb方向偏移5 mm、10 mm、15mm、20mm、25 mm、30 mm 6组仿真实验。在这6组仿真实验中，惯性器件的测量数据按照采样频率10 kHz从有限元分析结果中提取。然后，利用重采样的方法，获得惯性器件采样频率分别为5 kHz、2 kHz、1 kHz、0.5 kHz的测量数据，用于分析不同采样频率对减振系统引入捷联惯性导航测量误差解算结果的影响。

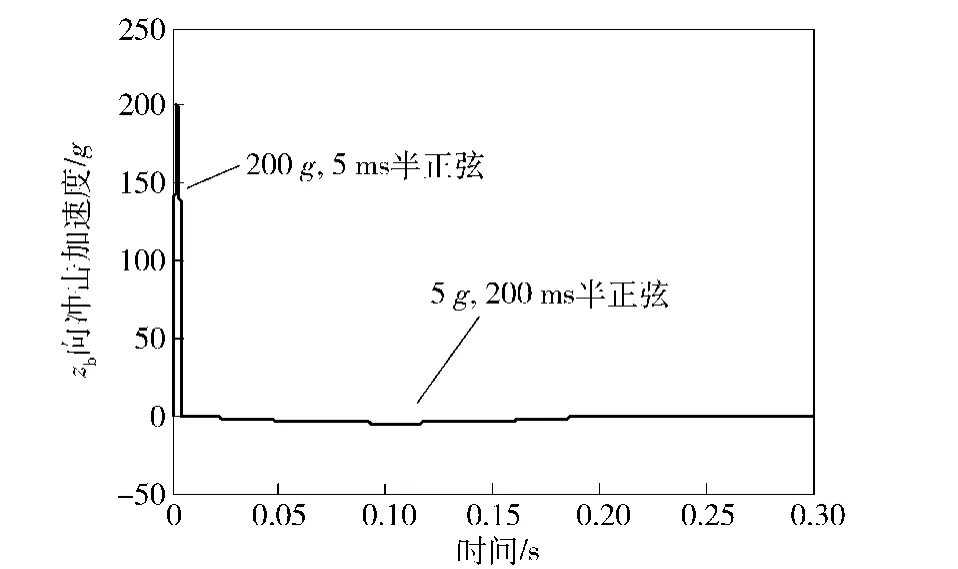
图5　冲击加速度激励Fig.5 Shock acceleration input

4.2方法准确性验证

传统轨迹仿真方法可以产生理想的惯性器件测量数据，其中忽略了包括减振系统在内的所有误差源。而基于有限元分析的方法，可以根据RP-1的运动数据得到只包含减振系统误差的惯性器件测量数据，用于分析减振系统引入的导航误差。同时也可以根据RP-13的运动数据得到不包含任何误差的惯性器件测量数据，通过与轨迹仿真方法产生的数据进行对比，可以验证基于有限元分析方法的准确性及有效性。

将传统轨迹仿真方法产生的惯性器件测量值作为真值，有限元方法提取的惯性器件测量数据误差如图6所示。由图6可见，zb方向加速度计误差最大，接近0.005m/s2，但该方向加速度最大值达到了2 000m/s2，故误差是可以忽略的。而3个方向的陀螺数据均与轨迹仿真方法产生的数据完全相同，在整个仿真实验过程中保持恒值，不存在误差。

以上对比结果说明，通过在有限元软件中构建惯性系、载体系等坐标系，实现了惯性导航系统工作过程的模拟，准确提取到了惯性器件测量数据，可用于进一步的分析研究。

4.3导航误差分析

惯性导航系统质心相对于弹性中心沿xb方向的偏移，导致绕yb方向的角振动与沿zb方向的线振动存在耦合，使得冲击作用对横滚角、东向速度、东向位置的精度造成了影响，对其他状态量的测量精度不造成影响。从不同偏移量的6组仿真结果中，分别提取惯性器件测量数据进行导航解算，得到减振系统造成的导航误差如图7所示。由图7可见，偏移量越大，造成的导航误差越大，横滚角误差和东向速度误差在冲击作用结束之后基本保持不变，而东向位置由于是东向速度对时间的积分，因此冲击结束后仍继续线性发散。由于导航系统一般需要连续工作较长时间，故假设未来1 h内载体不再受到任何冲击振动作用，根据速度误差恒定，位置误差呈线性发散，近似推算了冲击结束后1 h东向位置误差，结果如表1所示。

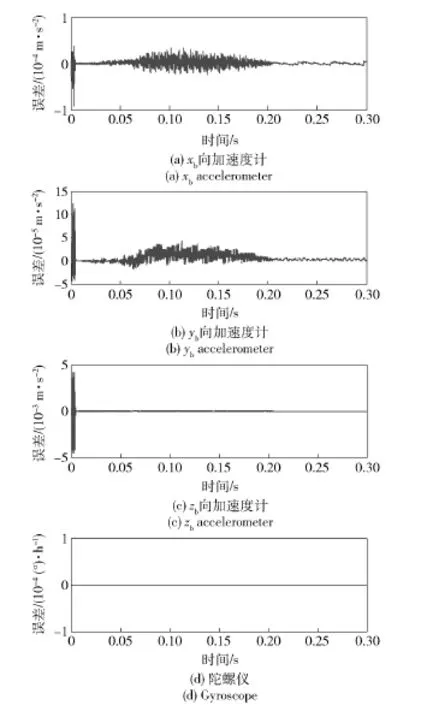
图6　惯性器件测量数据有限元提取误差Fig.6 Errors of measured data of inertial devicesextracted by FEA

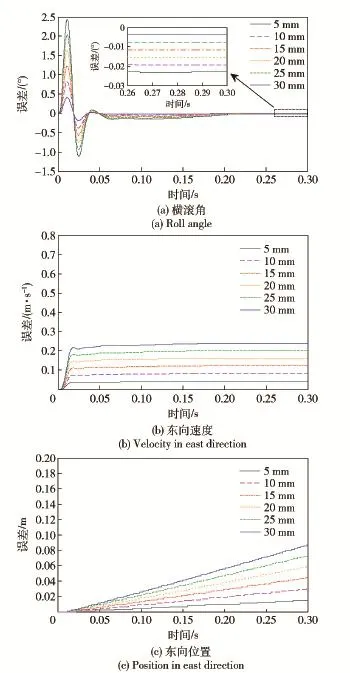
图7　不同偏移量情况下减振系统造成的导航误差Fig.7 Errors caused by vibration isolation system in the case of different offsets

表1　不同偏移量情况下冲击结束后1 h导航误差Tab.1 Navigation errors for 1 h after shock in the case of different offsets

从偏移量10mm的仿真结果中，提取不同采样频率下的惯性器件测量数据，进行导航解算，得到的导航误差如图8所示。从横滚角误差看，不同采样频率的影响并不大，而从东向速度和东向位置看，采样频率越高，由于减振器变形产生的系统误差就越小。这说明提高采样频率对该误差具有改善效果，但随着采样频率的提高，这种改善效果逐渐减弱，表2所示为不同采样频率情况下，冲击结束后1 h东向位置误差。

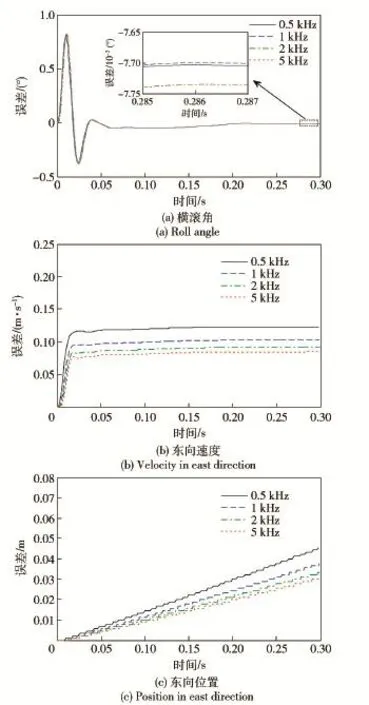
图8　不同采样频率情况下减振系统造成的导航误差Fig.8 Errors caused by vibration isolation system at different sampling frequencies

对有限元结果中提取的惯性器件测量数据进行解算，成功实现了减振系统对捷联惯性导航精度影响的定量分析。关于不同偏移量及不同采样频率的分析，对于带减振器的捷联惯性导航系统设计具有一定的指导意义。

表2　不同采样频率情况下冲击结束后1 h导航误差Tab.2 Navigation errors for 1 h after shock at different sampling frequencies

5　结论

针对减振系统在改善捷联惯性导航系统工作环境，提高测量精度的同时，会引入新误差源的问题，本文分析了减振系统对捷联惯性导航精度产生不良影响的原因；建立系统有限元模型，在有限元软件中模拟载体及惯性导航系统运动过程；通过进行坐标系定义，实现了从有限元动力学分析结果中提取惯性器件测量数据。由于分析过程中对减振系统变形之外的所有误差源进行了理想化处理，因此，经导航解算，便可以得到减振系统造成的惯性导航误差。

在验证有限元方法能够有效实现减振系统造成捷联惯性导航误差定量分析的基础上，对惯性导航系统质心相对于减振系统弹性中心存在偏移量不同、惯性器件采样频率不同，分别进行了多组仿真分析。研究结果表明，进行减振系统设计时，可以采用本文提出的方法从惯性导航测量精度的角度实现系统优化设计，具有一定工程应用参考价值。

（References）

［1］ Lahham J I，Wigent D J，Coleman A L.Tuned support structure for structure-borne noise reduction of inertial navigator with dithered ring laser gyros（RLG）［C］∥Position Location and Navigation Symposium.San Diego，CA，US:IEEE，2000:419-428.

［2］ Jaffe R，Aston T，Madni A M.Advances in ruggedized quartz MEMS inertial measurement units［C］∥Position，Location，and Navigation Symposium.San Diego，CA，US:IEEE，2006:390-399.

［3］ Spiewak S，Karpachevskyy T，Zaiss C.High performance isolation and excitation of vibration for enhanced identification of inertial sensors［C］∥ASME 2013 International Mechanical EngineeringCongress and Exposition.San Diego，CA，US:ASME，2013.

［4］ 杨富锋，芮筱亭，马蕾.激光陀螺捷联惯导减振系统动力学建模与仿真［J］.中国惯性技术学报，2008，16（3）:301-305. YANG Fu-feng，RUI Xiao-ting，MA Lei.Dynamical model and simulation of laser gyro strapdown inertial navigation system［J］. Journal of Chinese Inertial Technology，2008，16（3）:301-305.（in Chinese）

［5］ 王旭，张嵘.惯性导航系统并联缓冲器动力学分析与仿真［J］.中国惯性技术学报，2013，21（5）:561-564，569. WANG Xu，ZHANG Rong.Dynamical analysis and simulation of parallel bumper for INS［J］.Journal of Chinese Inertial Technology，2013，21（5）:561-564，569.（in Chinese）

［6］ 刘昱，王伟，李城锁.激光陀螺捷联惯导系统IMU结构模态分析［J］.中国惯性技术学报，2012，20（3）:273-277. LIU Yu，WANG Wei，LI Cheng-suo.Modal analysis for IMU of ring laser gyro strap-down inertial navigation system［J］.Journal of Chinese Inertial Technology，2012，20（3）:273-277.（in Chinese）

［7］ 程文娟，白真，何宁.基于有限元算法的惯导缓冲减振机构设计［J］.弹箭与制导学报，2014，34（6）:47-50. CHENG Wen-juan，BAI Zhen，HE Ning.Optimized design on vibration-isolation of inertial navigation by using finite element method［J］.Journal of Projectiles，Rockets，Missiles and Guidance， 2014，34（6）:47-50.（in Chinese）

［8］ 周亚东，董萼良，吴邵庆，等.惯性导航平台角振动抑制技术［J］.东南大学学报:自然科学版，2013，43（1）:60-64. ZHOU Ya-dong，DONG E-liang，WU Shao-qing，et al.Restricting method for angular vibration of inertial navigation platform［J］.Journal of Southeast University:Natural Science Edition，2013，43（1）:60-64.（in Chinese）

［9］ 洪华杰，王学武，杨光，等.武装直升机用稳定平台减振器特性的仿真研究［J］.兵工学报，2009，30（12）:1647-1652. HONG Hua-jie，WANG Xue-wu，YANG Guang，et al.Character simulation research on the absorber for stabilized platform on the armed copter［J］.Acta Armamentarii，2009，30（12）:1647-1652.（in Chinese）

［10］ LIJL，FANG JC，Ge SZ.Kinetics and design of a mechanically dithered ring laser gyroscope position and orientation system［J］.IEEE Transactions on Instrumentation and Measurement，2013，62（1）:210-220.

［11］ Abrahamsson T JS，Kammer D C.Finite element model calibration using frequency responses with damping equalization［J］. Mechanical Systems and Signal Processing，2015，62/63:218-234.

［12］ Arslan M E，Durmus A.Modal testing and finite element model calibration of in-filled reinforce concrete frames［J］.Journal of Vibration and Control，2014，20（13）:1946-1959.

FEA Method for Analysis of SINS Error Caused by Vibration Isolation System

GAO Jun-qiang，TANG Xia-qing，HUANG Xiang-yuan，CHENG Xu-wei
（Department of Control Engineering，Academy of Armored Force Engineering，Beijing 100072，China）

In order to study the strapdown inertial navigation system（SINS）error caused by vibration isolation system which breaks the fixed connection between SINS and carrier，the error mechanism is analyzed，and an analysis method based on finite element analysis（FEA）is proposed.A model of SINS with vibration isolation system is constructed in FEA software.The motion parameters generated by trajectory generator are used to simulate the motion processes of carrier and SINS.The measured data of inertial devices obtained from the FEA results can be used to resolve and acquire the SINS error caused by vibration isolation system.The research results show that the FEA-based method can realize the quantitative analysis of SINS error caused by vibration isolation system，which is very important for optimization design of vibration isolation system.

ordnance science and technology；strapdown inertial navigation system；vibration isolation system；error；finite element analysis

TJ819

A

1000-1093（2016）09-1570-08

10.3969/j.issn.1000-1093.2016.09.003

2016-01-06

军队科研计划项目（2011年）

高军强（1989—），男，博士研究生。E-mail:gjqxkl8990@163.com；汤霞清（1965—），男，教授，博士生导师。E-mail:tangxiaqing_001@163.com