一种星下点精确重访约束下的轨道设计方法

卫国宁，骆剑，康志宇，唐生勇，陈晓光

1.上海宇航系统工程研究所，上海 201109 2.上海航天技术研究院，上海 201109



一种星下点精确重访约束下的轨道设计方法

卫国宁1,*，骆剑2，康志宇1，唐生勇1，陈晓光1

1.上海宇航系统工程研究所，上海 201109 2.上海航天技术研究院，上海 201109

针对给定星下点的精确重访轨道设计，提出了一种已知两星下点精确重访约束下的圆回归轨道设计方法。分析了卫星的地心矢量同星下点地心矢量的关系，将精确星下点重访约束轨道设计问题转换为惯性坐标系内的一个动矢量同动坐标系内一个定矢量在惯性系下的重合问题。建立了不同轨道参数各自对应的目标函数，通过对目标函数零点的搜寻确定相应轨道参数，完成轨道设计。计算及仿真结果表明，所提出的构造目标函数并搜索零点的方法能够设计出满足约束条件的轨道，达到了预期目标。

星下点；精确重访；轨道设计；回归轨道；仿真

当前空间对地遥感任务正在由广域战略普查型向特定区域方向战术详查型发展。通常详查载荷受自身较窄观测视场约束，要求卫星对地面多个感兴趣的地点，具有精确重访能力。因此，精确星下点重访约束的轨道设计成为新的需求。近圆回归轨道以轨道高度均匀、星下点定时回归等特点在精确星下点重访任务中被广泛采用。

当前，卫星轨道参数确定时，星下点的计算理论已经较为完备[1-2]，但已知星下点约束时对轨道的设计尚没有成熟的系统方法。Abdelkahlik[2]考虑了卫星对地面的覆盖带，采用遗传算法提出了一种能够使卫星对多个给定星下点的分辨率综合达到最高的轨道设计方法，该方法的成功执行依赖于给定星下点的位置，设计结果为非圆轨道且不满足回归特性，不能满足精确重访给定星下点的需求。Abdelkahlik等[3]另提出了一种二体问题下基于星下点的轨道初始设计方法，以偏心率和半长轴为设计变量对轨道进行设计，并给出了数值解法。该方法能够完成星下点精确重访约束，但同样未考虑轨道的回归特性且设计结果为非圆轨道。段方等[4]以半长轴和轨道倾角为设计变量，提出了一类已知卫星的星下点反算近圆回归轨道的方法，但该方法仅适用于卫星在单个轨道上升段内星下点过两地的情形。

对地面任意给定两点精确重访的轨道设计是本文解决的问题。将精确星下点重访约束下的轨道设计为近圆回归轨道，以历元起始时刻的半长轴、轨道倾角、升交点赤经为设计变量，给出了已知星下点及重访周期约束时，单个和多个轨道周期内经过两地的近圆回归轨道设计方法。之后结合具有较高应用价值的太阳同步轨道，给出了星下点精确重访的准太阳同步回归近圆轨道的设计方法。同文献[3-5]不同的是，本文的方法能够求解出给定约束条件下星下点过A、B近圆回归轨道解的边界。设计的方法给出了算例，并对计算结果进行了可视化校验。

1　单轨道周期内星下点过两地近　 圆回归轨道设计

1.1坐标系定义及转换

(1)

式中：f=0.003 353，为地球扁率。地球非球形引力摄动J2项是引起轨道参数长期变化的主要因素，本文仅考虑J2项对各轨道参数的摄动情形。J2项摄动下，轨道参数半长轴a、偏心率e、轨道倾角i的长周期平均轨道参数不变。其他轨道参数摄动变化为[4]：

(2)

式中：Ω为升交点赤经；μ为地球引力常数；Re为地球平均半径；ω为近地点幅角；u为纬度幅角。本文所设计轨道的偏心率、起始时刻近地点幅角和纬度幅角均为0。

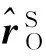
(3)

(4)

式中：ΔλIB为xI轴同xB轴的夹角，从北极上空看，逆时针方向为正。设起始时刻两者夹角为λIB0，则

(5)

式中：ωE为地球自转角速度。三个坐标系及星下点过A、B两地的示意见图1。

图1　坐标系定义及星下点过A、B两地示意Fig.1　Coordinate systems definition and ground track visiting A/B sites

1.2轨道倾角设计

给定星下点，该点对应的纬度幅角[1]

(5)

针对B′地落入I区的情形，有

(6)

(7)

1.3升交点赤经设计

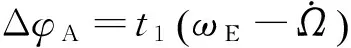
(8)

起始时刻B地赤经同惯性系xI轴夹角为λIB0，A地与B地经度差为λA-λB，则起始时刻的升交点赤经

(9)

(10)

式中：N为非负整数。则有当卫星起始时刻升交点赤经为ΩN时，卫星运行N圈后，第N+1圈的星下点轨迹经过A地。

1.4回归轨道设计

若卫星经过D个恒星日，运行C圈后地面轨迹开始重复，这样的轨道便是回归轨道[3]。地球相对轨道面旋转一周时间间隔为[6]

卫星两次过升交点的时间间隔，即轨道周期[7]

对于回归轨道TE和TΩ满足

CTΩ=DTE

得[4]

(11)

若给定D、C、i，构造半长轴a的函数

(12)

满足g(a)=0的半长轴a即为所求。若a大致范围已知，给出天数D约束，则能得出大致的圈数C的取值范围，通过式(12)能够得到D天内所有满足回归条件的半长轴a。

通过目标函数g(a)、f(i)零点的求解,可得满足单轨道周期内星下点过A、B两地的回归轨道半长轴a和轨道倾角i，同时由式(10)可得轨道的升交点赤经。此时，起始时刻卫星的轨道六要素全部确定，完成轨道设计。

2　多轨道周期星下点过两地近圆　 回归轨道设计

航天器在轨执行任务时，通常只需星下点经过期望的地区即可，并不强调在单个轨道周期内完成期望地区的覆盖，因此有必要进行多个轨道周期内星下点过期望地区的轨道设计。

多轨道周期星下点过两地轨道存在性说明。记卫星星下点过A地的轨道为第1圈，之后卫星每过一次升交点轨道圈数加1。设第L圈的时候星下点经过B地，如图2所示。

图2　多个轨道周期内星下点过A、B两地示意Fig.2　Ground track visits A/B sites within multiple cycles

这里只需完成轨道倾角的设计。星下点从经过A地对应轨道段的升交点开始到第L圈经过B′地，卫星一共转过地心角

(13)

uB′的计算见第1.2节，对应时间

(14)

半长轴a、升交点赤经ΩN的设计同第1节，起始时刻卫星的轨道6要素全部确定，完成轨道设计。

3　星下点过两地的准太阳同步近　 圆回归轨道设计

(15)

给定轨道倾角i，则由式(15)可得太阳同步圆轨道的半长轴a。则两相邻星下点轨迹之间对应地心夹角

(16)

可得到星下点分别过A、B两地的两个轨道段，设两者升交点对应的星下点分别为Ar、Br。由第1.3节可得ΔΩA，同理可得ΔΩB，则连接Ar、Br的弧所对应的地心角

(17)

回归轨道星下点过A、B两地示意见图3。

图3　太阳同步回归轨道星下点过A、B两地示意Fig.3　Repeating sun synchronous orbit ground track visits A/B sites

构造函数

(18)

理论上讲，只要回归时间足够长，星下点能够覆盖地球所有地区，所以星下点过A、B两地的太阳同步回归轨道一定存在，但受到任务的约束，回归天数通常不能过长，所以可能存在无解的情况，可以适当放宽h(i)的取值范围。

4　方法应用

已知星下点和回归周期约束下轨道设计的关键在于通过求解各目标函数零点得到轨道倾角、升交点赤经和半长轴。因为3个参数相互耦合且非线性因素较多，若采用解析的方法直接求解，会造成较大困难，适宜采用数值解法。

4.1轨道倾角和半长轴设计方法应用

(1)单轨道周期内过两地情形

i已知时，给定回归天数和圈数，函数g(a)为只与半长轴a有关的函数。搜索函数零点，可得给定回归天数约束下所有满足回归条件的a值。

(2)L个轨道周期内过两地情形

首先给定L的值，分别针对B地落入I～IV区4种情形利用式(13)、式(14)解得从第L圈经过B′地的时间t2。得到t2后轨道倾角和半长轴的设计同单个轨道周期内过A、B两地情形相同，不再详述。

(3)准太阳同步回归圆轨道设计情形

4.2升交点赤经设计方法应用

给定N，将第4.1节所得Ω1带入式(10)，可得第N+1圈星下点过A地轨道的升交点赤经ΩN。

5　算例及仿真校验

5.1单轨道周期星下点过两地近圆回归轨道设计

按照第4节中对应执行算法，得到3条满足约束的轨道，表1给出了这3条轨道对应的半长轴a，轨道倾角i，起始时刻升交点赤经Ω及各轨道对应的回归天数D和回归圈数C。选择编号为1的轨道进行可视化校验，见图4。

表1　单个轨道周期内星下点过A、B两地的轨道参数

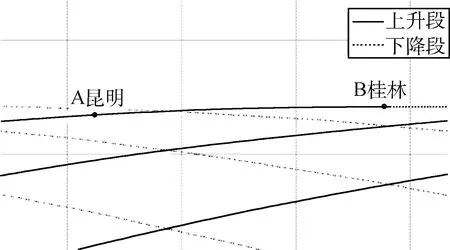
图4　轨道1对应90天内星下点轨迹可视化校验(N=0)Fig.4　90 days ground track of orbit 1(N=0)

5.2多轨道周期星下点过两地近圆回归轨道设计

令轨道在经过A地2圈之后，第3圈过B地。得到3条回归轨道见表2，可视化校验见图5。

表2　3个轨道周期内星下点过A、B两地的轨道参数

图5　轨道4对应前三圈星下点轨迹可视化校验(N=0)Fig.5　Ground track of the 1st three circles for orbit 4(N=0)

5.3星下点过两地准太阳同步近圆回归轨道设计

执行对应算法发现无解，可适当放宽ξ4约束，令ξ4=0.01，得星下点近似过A、B两地的两条太阳同步回归轨道，相关参数见表3，可视化校验见图6。

表3　过A、B两地的太阳同步回归轨道轨道参数

6　结束语

本文研究了一种已知星下点A、B，考虑J2项摄动时的精确星下点重访约束下的轨道设计问题。针对卫星轨道在单轨道周期、多轨道周期内星下点过两地的不同情形，通过对构建的以轨道倾角为变量的目标函数零点的搜索，完成了轨道倾角的设计；在回归天数和回归轨道圈给定情况下，通过对构建的以半长轴为变量的目标函数零点的搜索，完成了回归轨道半长轴的设计；给出卫星升交点赤经的计算公式，确定了满足星下点过A、B两地的轨道的解的边界。同样通过构建目标函数搜索零点的方式进行了星下点A、B的太阳同步回归轨道的设计。最后，给出具体算例，并对结果进行了可视化校验。结果显示，该方法能够较好地解决已知两星下点情况下对轨道的反设计问题。后续工作将考虑相机视场，对ξ取值与星下点覆盖带宽度的影响进行分析，并对卫星进行轨道机动情形下多个星下点约束的精确重访轨道设计问题进行研究。

References)

[1]杨嘉.航天器轨道动力学与控制(上)[M].北京：中国宇航出版社，2009:152-164.

[2]ABDELKHALIK O. Initial orbit design from Ground track points[J]. Journal of Spacecraft and Rockets, 2010, 47(1):202-205.

[3]ABDELKHALIK O, MORTARI D. Orbit design for ground surveillance using genetic algorithms[J]. Journal of Guidance Control and Dynamics, 2006, 29(5):1231-1235.

[4]段方，刘建业. 一类由星下点反算卫星近圆回归轨道的方法[J]. 中国空间科学技术，2006，26(6): 38-42.

DUAN F, LIU J Y. Calculation method of a kind of near round repeating satellite orbit using nadir points[J]. Chinese Space Science and Technology, 2006, 26(6):38-42(in Chinese).

[5]VTIPIL S, NEWMAN B. Determining an earth observation repeat ground track orbit for an optimization methodology[J]. Journal of Spacecraft and Rockets, 2012, 49(1), 157-164.

[6]FU X F, WU M P,TANG Y. Design and maintenance of low-earth repeat ground track successive coverage orbits[J]. Journal of Guidance Control and Dynamics, 2012, 35(2): 686-691.

[7]NADOUSHAN M J, ASSADIAN N. Repeat ground track orbit design with desired revisit time and optimal tilt[J]. Aerospace Science and Technology, 2014,40(11): 200-208.

[8]赵坚.太阳同步(准)回归轨道卫星的轨道保持方法研究[J]. 中国空间科学技术，2004,24(4):60-64.

ZHAO J.Reasearch on the orbit keeping of the sun-synchronous repeating orbit[J].Chinese Space Science and Technology,2004,24(4):60-64(in Chinese).

(编辑：高珍)

A method of orbit design based on precise revisit of a given ground track

WEI Guoning1,*, LUO Jian2, KANG Zhiyu1, TANG Shengyong1, CHEN Xiaoguang1

1.Aerospace System Engineering Shanghai, Shanghai 201109, China 2.Shanghai Academy of Spacelight Technology, Shanghai 201109, China

A new orbit design method is needed for precise revisit the given ground track points. A method of designing precise revisit of 2 given ground track round repeating orbit was proposed. The relationship between the satellite geocentric vector and the ground track geocentric vector was analyzed; the problem was converted to the coincidence problem in the inertial coordinate system of a motion vector in inertial coordinate system and a constant vector in the moving coordinate system. Different target functions were constructed,while orbit elements were obtained by searching the zeros of the corresponding function. Calculation and simulation results demonstrate the effectiveness of the proposed approach.

ground track point;precise revisit;orbit design;repeating orbit;simulation

10.16708/j.cnki.1000-758X.2016.0049

2015-12-10；

2016-05-17；录用日期：2016-06-30；

时间：2016-08-0214:19:55

http:∥www.cnki.net/kcms/detail/11.1859.V.20160802.1419.001.html

上海市科学技术委员会资助课题(14XD1423400)

卫国宁(1991-)，男，硕士研究生，wgn517@email,主要研究方向为航天器轨道设计、飞行器总体设计

V412.41

A

http:∥zgkj.cast.cn

引用格式：卫国宁，骆剑，康志宇，等.一种星下点精确重访约束下的轨道设计方法[J].中国空间科学技术,2016,36(4):

67-73.WEIGN,LUOJ,KANGZY,etal.Amethodoforbitdesignbasedonpreciserevisitofagivengroundtrack[J].ChineseSpaceScienceandTechnology,2016,36(4):67-73(inChinese).