空间物体解体碎片云的长期演化建模与分析
2016-11-09张斌斌王兆魁张育林
张斌斌,王兆魁,张育林,2
1.国防科技大学 航天科学与工程学院,长沙 410073 2.清华大学 航天航空学院,北京 100084
空间物体解体碎片云的长期演化建模与分析
张斌斌1,王兆魁2,*,张育林1,2
1.国防科技大学航天科学与工程学院,长沙 410073 2.清华大学航天航空学院,北京 100084
空间碎片云由空间物体解体产生的大量空间碎片组成,由于其相对集中地分布在有限的空间内,将会对临近航天器产生较大的碰撞威胁。为了分析解体碎片云长期分布特点,文章首先利用数值积分方法对空间碎片云短期分布规律进行了研究;在此基础上,针对处于环状分布的碎片云,根据碎片所在的轨道高度和具有的面质比值,将碎片划分到不同分组,以每个组作为研究对象,建立了描述碎片云在大气阻力作用下的解析演化模型。模型避免了对单个解体碎片的运动状态进行积分,可大大降低对计算资源和计算时间的需求。考虑在高度为1 422 km圆轨道上运行的物体,解体产生了1 780个碎片,利用解析演化模型得到碎片云未来50年内的演化分布状态。数值结果表明,碎片云的峰值密度在解体物体轨道高度附近,并在大气阻力作用下向更大高度区间内扩散;较低高度区间内碎片密度具有先增加,然后在大气阻力作用下不断减少的特点。
空间碎片云;空间密度;解体模型;碎片分布;演化模型
空间碎片云由大量解体碎片构成,这些解体碎片由火箭上面级、在轨运行航天器等人造物体解体产生。随着人类航天活动的不断增加,由空间物体相互碰撞而解体产生的空间碎片数量日益增多,截止到2016年6月,已经记录的空间物体超高速灾难性碰撞解体事件有4次,分别是1991年COSMOS 1934航天器和编目的13475号空间碎片碰撞,1996年法国“樱桃”号航天器和编目的18208号空间碎片碰撞,2005年THOR BURNER 2A火箭体与编目的26207号空间碎片碰撞,以及2009年COSMOS 2251航天器IRIDIUM 33航天器发生碰撞[1]。每次航天器的超高速剧烈碰撞事件,都会引入大量的解体碎片,如2009年COSMOS 2251和IRIDIUM 33碰撞解体产生2 201个编目碎片,占在轨总编目碎片数量的1/8。可以看出,空间物体之间相互碰撞形成的解体碎片,会对在轨工作航天器产生巨大的碰撞威胁,将是未来空间碎片增长主要原因[2-4]。对空间物体解体产生的碎片云的长期分布演化状态进行研究,对于分析预测空间碎片环境的未来演化趋势、分析航天器受碎片云的碰撞威胁等具有重要的意义。
空间碎片云的分布演化不仅与解体物体的质量、尺寸以及运动状态相关,还受大气阻力、非球形引力等复杂摄动力作用的影响。通常分别建立空间物体解体模型和长期演化计算模型,来分别描述空间物体解体产生碎片情况和碎片云的长期分布演化情况。文献中一般利用美国国家航空航天局(NASA)标准解体模型来模拟产生物体解体碎片[5],但该模型是有局限的,未能考虑解体过程中解体物体与碎片的质量和动量守恒。针对空间碎片分布的长期演化分析问题,文献[6]建立了空间碎片碰撞风险分析工具(SDIRAT);文献[7]设计了空间碎片仿真系统(SDS),利用该仿真系统得到,若星座卫星附近发生碰撞解体事件,解体碎片云将会使星座卫星受到的碰撞威胁急剧增加,但该仿真系统仅适合在几个小时或数月内对解体碎片云的分布状态进行仿真分析。上述空间碎片分布演化模型,以及文献[8]中建立的LEGEND模型、文献[9]中建立的SDM模型,均以单个解体碎片的运动状态为演化计算对象,当进行长期分析时,不仅需要较长计算时间,消耗大量计算资源,而且不能保证碎片云分布状态长期演化计算结果的精度[10]。
本文首先在NASA标准模型的基础上,通过数值模拟产生解体碎片;然后通过对解体碎片的运动状态进行数值积分,演化计算得到碎片云短期分布状态,进而分析得到碎片云的分布特点;最后,基于解体碎片云的分布特点,建立了大气阻力作用下空间碎片云的解析演化模型,并利用该解体模型分析了碎片云的长期分布演化状态。
1 解体模型和碎片云短期分布特点的数值分析
1.1解体模型及其数值仿真实现

(1)

(2)
利用式(2)可以确定每个解体碎片的尺寸。进一步可以通过下述双正态分布方程确定解体碎片的面质比:
(3)
在解体时刻,解体碎片获得相对于解体物体的速度增量Δv满足正态分布函数,即
(4)
综合空间物体解体产生碎片过程中质量守恒和动量守恒约束,利用解体模型模拟生成解体碎片的流程如图1所示。计算时,首先确定要研究解体碎片的最小尺寸lc,然后根据关系式(1)和计算解体产生大于尺寸碎片的总数目,再根据分布律式(2)、(3)和(4)确定解体碎片具有的尺寸、面质比和速度增量。应用分布律式(2)、(3)和(4)时,需要对随机变量抽样,可采用反函数的方法进行随机变量的抽样[11]。
以一颗Globalstar星座卫星受空间碎片碰撞解体为例,说明上述解体模型数值实现。Globalstar星座卫星质量约为800 kg,运行在高度为1 422 km的圆轨道上,解体时刻在J2000坐标系中的位置和速度矢量分别为r=[7 784.4 00 0 -0.001 305] km,v=[0 4.311 5.721] km/s。星座卫星受空间碎片碰撞后,完全解体,产生1 780个尺寸大于5 cm的碎片。利用解体模型模拟产生的碎片分布情况如图2和图3所示。
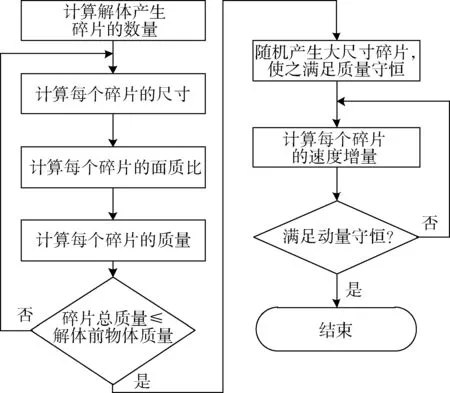
图1 NASA标准解体模型的实现流程Fig.1 Computation flow diagram of the breakup model
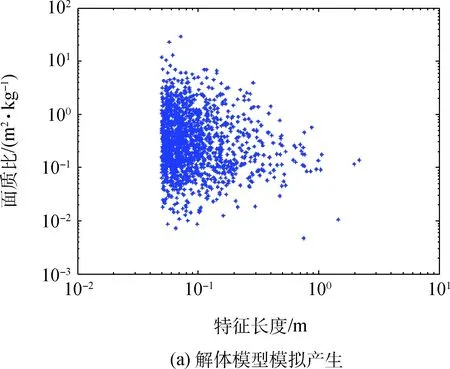
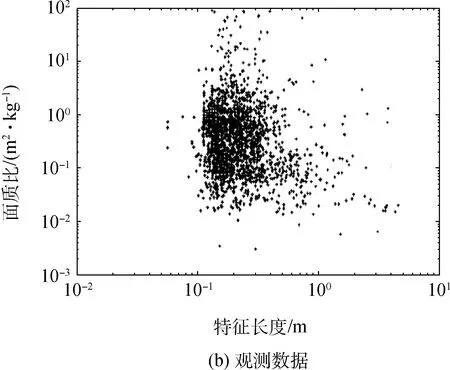
图2 解体碎片面质比分布的对比分析Fig.2 Breakup fragments′ area-mass ratio distribution
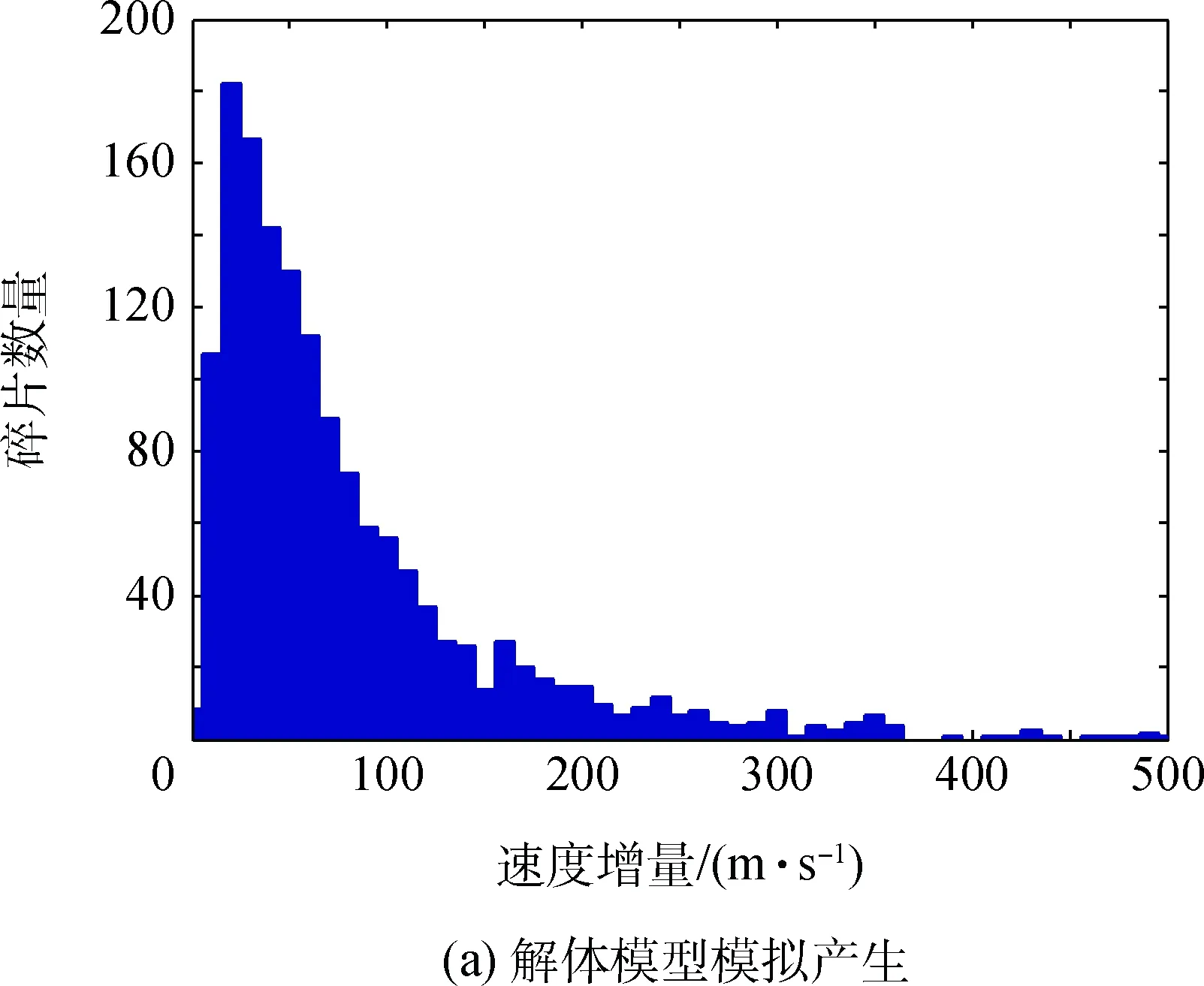

图3 解体碎片速度增量分布的对比分析Fig.3 Breakup fragments′ velocity increment distribution
图2(a)和图3(a)分别是利用解体模型模拟得到的解体碎片面质比分布和速度增量分布,图2(b)和图3(b)则是利用1 780个在轨解体碎片的长期观测数据,分析得到的解体碎片面质比分布和速度增量分布情况[5]。对比图2(a)和图2(b),图3(a)和图3(b)可以看出,利用解体模型得到的解体碎片的面质比、速度增量分布与实际观测数据一致,说明了解体模型和实现方法的正确性。
1.2碎片云分布特点分析
为了分析碎片云的分布特点,综合考虑大气阻力、地球非球形引力、太阳光压以及日、月三体引力等摄动力的作用,利用数值积分的方法对解体碎片的运动状态进行计算更新。数值计算中,大气阻力计算采用Harris-Priester大气模型,该模型能够反映太阳辐射对大气密度的长期影响,且计算复杂度较低;地球非球形引力中考虑了J2、J3和J4等带谐项,以及J2,2田谐项的影响;数值积分采用4阶Adams-Bashforth/Adams-Moulton预测修正方法,利用4阶Runge-Kutta方法进行积分的初始化[12]。
对第1.1节模拟生成的1780个解体碎片的运动状态进行数值积分计算,计算结果如图4~图6所示。
图4(a)、图5(a)、图6(a)给出了解体碎片云的空间密度,即单位空间体积内解体碎片的数量,在不同时刻、不同高度上的分布。图4(b)、图5(b)、图6(b)给出了解体碎片云在3维空间中的分布情况。对比图4~图6可以看出,解体碎片云的分布状态随时间演化大致可以分为3个阶段:集中分布阶段、带状分布阶段及环状分布阶段。空间物体解体后很短一段时间内,解体碎片处于集中分布阶段,如图4(a)所示,此阶段内解体碎片呈现密集团状分布,该分布特点主要由解体时刻碎片获取的速度增量决定。如图5(b)所示,由于解体碎片获取的速度增量不同,导致解体碎片的轨道周期和相位出现差异,经过1个月左右解体碎片云在近似一个轨道面上形成均匀的圆带状,进入了带状分布阶段。对比图4(a)和图5(a)可以看出,相比于集中分布阶段,带状阶段内的解体碎片不仅相位上呈现差异,也在逐渐向不同高度上扩散。在带状分布的基础上,受主要摄动力地球非球形J2项引力的作用:
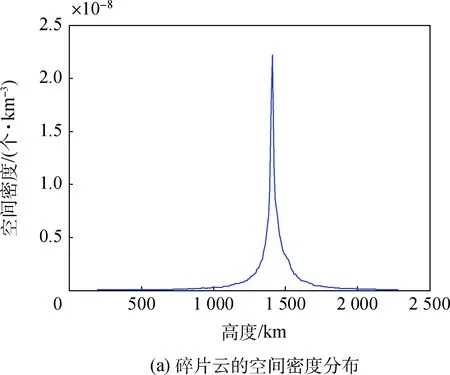
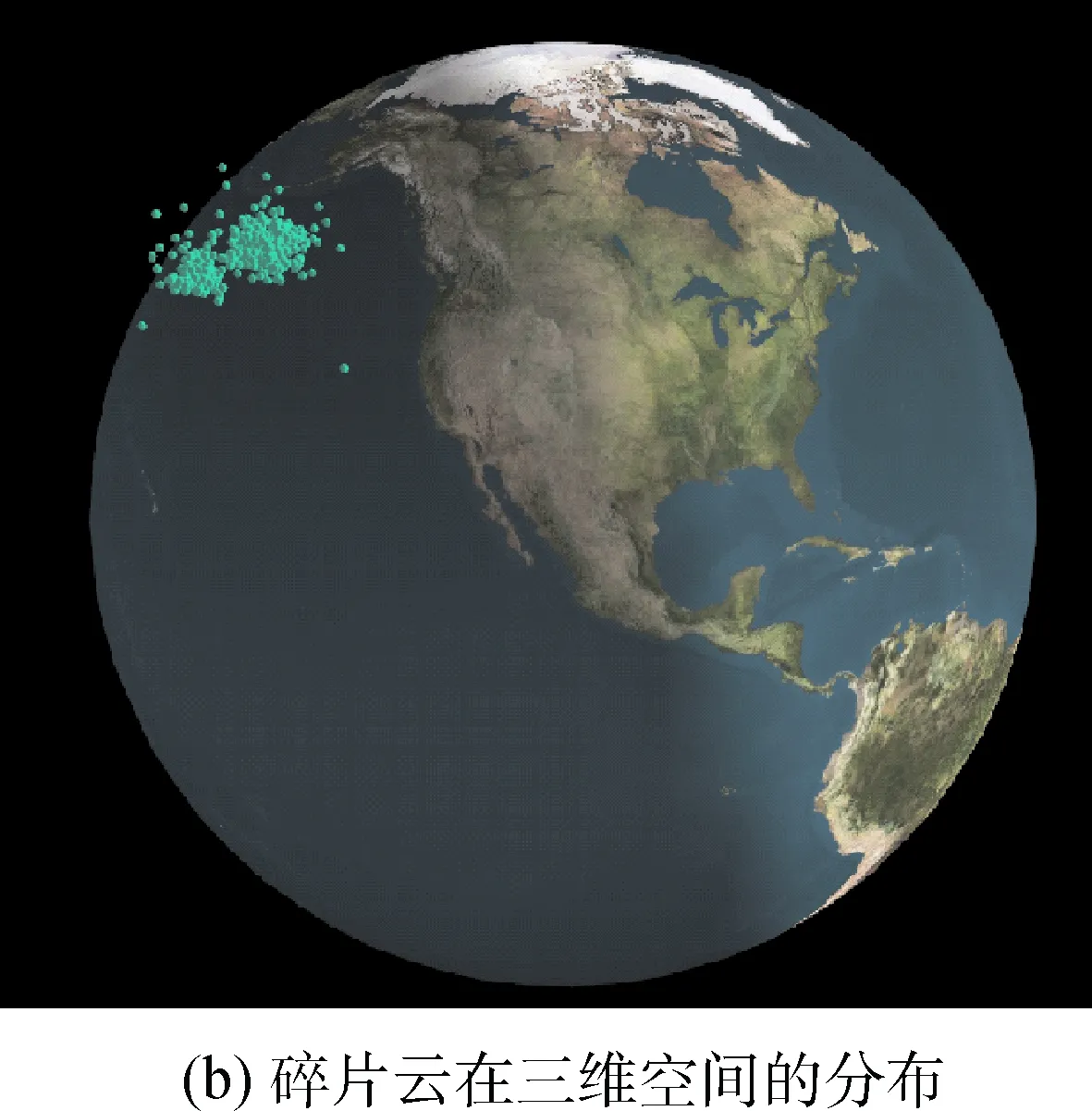
图4 物体解体时刻碎片云的空间分布Fig.4 Space cloud′s spatial density distribution when the breakup event accured
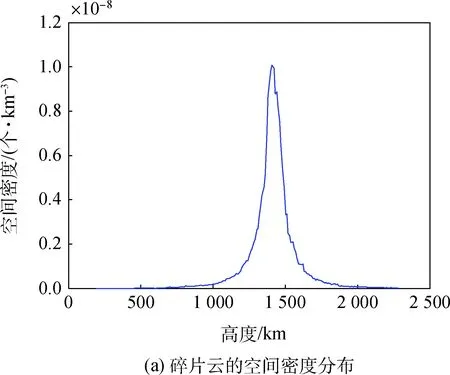

图5 物体解体后1个月尺寸大于5cm解体碎片的空间分布Fig.5 Space cloud′s spatial density distribution after the breakup event
(5)
式中:RE为地球半径;μ为地球引力常数;a、e和i分别为碎片轨道半长轴、偏心率和倾角。
不同解体碎片轨道的升交点赤经和近地点幅角的变化率呈现差异,并在一段时间后趋于均匀分布,形成环状分布,如图6(b)所示。碎片云进入环状分布阶段后,将主要在大气阻力作用下,沿轨道高度方向变化。

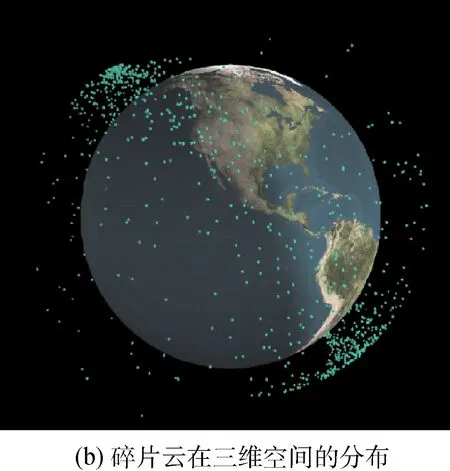
图6 物体解体后5个月尺寸大于5cm解体碎片的空间分布Fig.6 Space cloud′s spatial density distribution after the breakup event
从上述分析过程可以看出,利用数值积分方法,可以得到解体碎片在未来一段时间内的运动状态,进而分析解体碎片云的分布特点。但数值积分方法,以每个解体碎片为计算对象,对计算资源要求高,演化计算时间也较长。如在上述分析中,利用配置为32核(单核主频为2.13 GHz)的计算服务器,需要15 h的计算时间才能得到如图6(b)所示的碎片分布状态。
2 大气阻力作用下空间碎片云的解析演化模型
考虑到利用数值积分方法对解体碎片的运动状态进行长期演化分析,将需要大量计算资源和时间。本节将在一定假设的基础上,基于空间碎片云环状分布特点,将解体碎片云按高度进行分层离散化,以每个高度层内解体碎片作为一个整体进行研究,建立碎片云的解析演化模型,实现对碎片云分布状态的长期分析。
当解体碎片云进入如图6所示环状分布状态后,在地球非球形摄动力作用下,解体碎片轨道的纬度幅角和升交点赤经不断均匀变化,同一轨道高度上的解体碎片的分布将是均匀和相对稳定的。此后,解体碎片云将会在大气阻力的作用下,沿轨道高度方向变化。将解体碎片云按轨道高度划分到Nh个高度区间内。同时考虑到不同面质比物体,受到大气阻力摄动力不同,进一步将同一高度区间内的解体碎片划分到Na个面质比区间内。同一高度和面质比区间内的解体碎片可视为一个独立分组,以每个分组为研究对象,建立解体碎片云演化的微分控制方程,实现对碎片云分布的长期分布演化。
取第i高度区间为控制体,该控制体内物体轨道高度差为Δr,如图7所示。

图7 碎片云分布空间分层与控制体选取示意Fig.7 Grouping and control volume setting of space debris cloud
假设解体碎片均运行在圆轨道上,则在大气阻力摄动作用下,控制体内位于第j个面质比区间的解体碎片的状态变化:
(6)
式中:si,j(r,t)是第i高度区间和j个面质比区间内解体碎片的空间密度;vri,j(r)是在大气阻力作用下,第i高度区间和j个面质比区间内解体碎片轨道高度衰减的平均速度。从式(6)中可以看出,由于大气阻力作用进入和离开第i高度区的解体碎片数量的变化。
解体碎片的空间密度si,j(r,t):
(7)
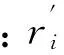
近地点地心距;分母中ak为碎片轨道半长轴。在大气阻力摄动作用下,解体碎片的平均衰减速度vri,j(r)利用高斯型一般摄动力方程组[13]求解:
(8)
式中:fu、fh和fn分别表示大气阻力沿解体碎片飞行速度方向、轨道面内垂直速度方向以及轨道面法向上的分量。基于指数大气密度模型,大气阻力各分量取值为
(9)
考虑解体碎片运行在圆轨道上,综合方程组式(8)和方程式(9)可以得到:
(10)
式中:CD是阻力系数;ρi0是参考椭球面r=ri0处的大气密度;Hi是参考密度标高。
令Δr→0,即研究极限情况下,同一高度上解体碎片的变化,得到描述解体碎片分布状态变化的连续偏微分模型为
(11)
式(11)是一阶拟线性偏微分方程。利用微分方程的特征线法,可以得到方程式(11)的解为
(12)
式中:εi,j定义为
(13)
式(12)是碎片云分布演化的解析表达式,描述了第i高度区间和j个面质比区间内的解体碎片,在不同高度上随时间的演化分布情况。可以看出,解体碎片的分布主要受到碎片初始分布状态和大气阻力作用的影响。Nh个高度区间和Na个面质比区间内解体碎片分布的累加,即为解体碎片云的分布:
(14)
3 空间碎片云分布状态的长期演化分析
在第1.2节中,利用数值积分计算方法,将1 780个解体碎片演化到环状分布状态。本节将利用第2节建立的解析演化模型,对处于环状分布的碎片云的长期分布特点进行分析。根据解体碎片的轨道高度和面质比,将碎片云划分为(Nh=210个高度区间)×(Na=10面质比区间)=2 100个分组。表1给出了碎片云的初始分布状态si,j(r,0)。

表1 2 100个碎片分组的初始空间密度si,j(r,0)
应用解析分布演化模型式(14),在配置为4核(单核主频为2.93 GHz)的个人计算机上,0.2 s内可以将碎片云的分布状态演化到未来的50年,结果如图8所示。分析长期分布演化结果可以得到以下结论:
1)碎片云的峰值密度在解体物体轨道高度附近,解体物体轨道高度附近的航天器将持续受到解体碎片云的碰撞威胁;
2)受大气阻力的作用,碎片云峰值空间密度随时间演化而减少,碎片云向更大高度区间内扩散;
3)由于峰值密度处解体碎片不断向低轨衰减,较低高度区间内碎片在一段时期内不断增加,如演化10年时刻的碎片云分布曲线所示,随后在大气阻力衰减作用下较低高度区间内碎片的密度也将不断减少。
4 结束语
随着空间碎片的不断增加,航天器受到碎片的碰撞威胁将会日益严重。在轨工作航天器、失效载荷及火箭上面级等空间大物体,由于爆炸或相互碰撞,解体产生的大量碎片将成为未来空间碎片不断增加的主要原因。本文提出的碎片云解析演化模型,描述了碎片云整体分布演化特点,能够反映大气阻力等主要摄动力对解体碎片云分布的影响。利用该模型,能够快速地获取碎片云的长期演化状态,从而为评估碎片云对航天器产生的碰撞威胁、分析空间物体解体作用对近地轨道碎片环境的长期影响提供长期的碎片分布状态数据输入。
References)
[1]PARDINI C,ANSELMO L. Review of past on-orbit collisions among cataloged objects and examination of the catastrophic fragmentation concept [J]. Acta Astronaut.,2014,100: 30-39.
[2]LIOU J C. Collision activities in the future orbital debris environment[J]. Advances in Space Research,2006,38(9): 2102-2106.
[3]WANG T. Analysis of debris from the collision of the Cosmos 2251 and the Iridium 33 satellites[J]. Science & Global Security,2010,18: 87-118.
[4]ZHANG Y L,WANG Z K. Space traffic safety management and control[J]. Intelligent Transportation Systems,IEEE Transactions on,2015,PP99: 1-4.
[5]JOHNSON N L,KRISKO P H,LIOU J C,et al. NASA′s new breakup model of evolve 4.0[J]. Advances in Space Research,2001,28(9): 1377-1384.
[6]PARDINI C,ANSELMO L. Assessing the risk of orbital debris impact[J]. Adv. Space Res.,1999,1(1): 59-80.
[7]SWINERD G G,BARROWS S P,CROWTHER R. Short-term debris risk to large satellite constellations[J]. J. Guid. Control Dynam.,1999,22(2):291-295.
[8]LIOU J C,HALL D T,KRISKO P H,et al. LEGEND-a three-dimensional LEO-to-GEO debris evolutionary model[J]. Advances in Space Research,2004,34(5): 981-986.
[9]ROSSI A,ANSELMO L,PARDINI C,et al. The new space debris mitigation(SDM 4.0)long-term evolution code[C]∥Proceedings of the 5th European Conference on Space Debris,Noordwijk,The Netherlands,2009.
[10]NAZARENKO A I. Prediction of the space debris spatial distribution on the basis of the evolution equations[J]. Acta Astronaut.,2014,100(1):47-56.
[11]高惠璇. 统计计算[M]. 北京:北京大学出版社,1995.
GAO H X. Statistical computation[M]. Beijing: Peking University Press,1995.
[12]MONTENBRUCK O,GILL E. Satellite orbits: models,methods and applications[M]. Berlin:Springer Science & Business Media,2012.
[13]郗晓宁,王威. 近地航天器轨道基础[M]. 长沙:国防科技大学出版社,2003.
XI X N,WANG W. Fundamentals of near-Earth spacecraft orbit[M]. Changsha: National University of Defense Technology Press,2003.
(编辑:车晓玲)
Modeling and analysis on the long-term evolution of the space debris cloud
ZHANG Binbin1,WANG Zhaokui2,*,ZHANG Yulin1,2
1.College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China 2.School of Aerospace Engineering,Tsinghua University,Beijing 100084,China
A space debris cloud consists of numerous breakup fragments which are originated from an instinct space object. As the breakup fragments are in a concentrated distribution,those spacecraft in the neighborhood of the breakup objects will face a serious threat of collision. In order to evaluate the long-term evolution of space debris,the propagation of space debris cloud for a short-term period was analyzed numerically.Based on the stable distribution characteristic of the debris cloud,fragments were divided into several groups according to their orbital heights and area-mass ratios. The long-term distribution under the perturbation of atmosphere drag was described by an analytic evolution model. Comparing with all the fragments propagating individually,the analytic model was more efficient and less time-consuming. The evolution of a breakup debris cloud consists 1 780 breakup fragments,and was obtaired for the next fifty years. Results show that the peak spatial density of the debris cloud is around the height of the breakup object and will spread into a broader height interval continuously,and the fragments in the lower height interval will firstly increase and then decrease under the perturbation of air drag.
space debris cloud;spatial density; breakup model;debris distribution;evolution model
10.16708/j.cnki.1000-758X.2016.0046
2016-03-31;
2016-07-01;录用日期:2016-06-30;
时间:2016-08-0214:20:06
http:∥www.cnki.net/kcms/detail/11.1859.V.20160802.1420.003.html
国家自然科学基金(11572168)
张斌斌(1987-),男,博士研究生,zhangbinbin10@126.com,研究方向为航天器动力学与控制、空间碎片演化建模与分析
王兆魁(1978-),男,教授,wangzk@tsinghua.edu.cn,主要研究方向为航天器动力学与控制
V528
A
http:∥zgkj.cast.cn
引用格式:张斌斌,王兆魁,张育林. 空间物体解体碎片云的长期演化建模与分析[J].中国空间科学技术,2016,36(4):1-8.
ZHANGBB,WANGZK,ZHANGYL.Modelingandanalysisonthelong-termevolutionofthespacedebriscloud[J].ChineseSpaceScienceandTechnology,2016,36(4):1-8 (inChinese).
