基于D-S证据理论的航天设备寿命预测方法

丁瑞，陆宁云，*，程月华，姜斌，邢琰

1.南京航空航天大学 自动化学院，南京 211016 2.南京航空航天大学 航天学院，南京 211016 3.北京控制工程研究所，北京 100191 4.空间智能控制技术国家重点实验室，北京 100191



基于D-S证据理论的航天设备寿命预测方法

丁瑞1，陆宁云1，*，程月华2，姜斌1，邢琰3,4

1.南京航空航天大学 自动化学院，南京 211016 2.南京航空航天大学 航天学院，南京 211016 3.北京控制工程研究所，北京 100191 4.空间智能控制技术国家重点实验室，北京 100191

以动量轮为研究对象，提出一种基于D-S证据理论和Bayes理论的信息融合及寿命预测方法。首先，挖掘多个寿命信息源的内、外部信息作为Bayes多源验前信息，并构建证据集合；其次，利用合成规则对证据集合进行合成，得到合理的验前融合权重的分配结果；然后，利用Bayes方法求解寿命参数的融合验后分布，并计算寿命参数的估计值；最后，根据参数估计值预测设备的剩余寿命。仿真结果表明，基于多源寿命信息融合的预测结果与单一来源的寿命预测结果相比，更加接近于设备的真实寿命信息。

寿命预测；多源信息融合；D-S证据理论；Bayes方法；动量轮

航天设备运行机理复杂，运行环境恶劣，设备性能退化过程中容易导致恶性事故发生。为保障航天器安全可靠运行，确保航天任务顺利实施，准确的设备剩余寿命预测方法是航天工程中的迫切需求。航天设备具有典型的小子样特点，不适合使用传统的基于大样本寿命数据的预测方法[1-2]。然而，航天设备在设计、研制、试验和使用等阶段均存在不同来源、不同环境及不同层次的寿命信息，对这些多源寿命信息进行合理融合，将有助于得到更准确的设备剩余寿命预测结果。

信息融合的最初定义是指，对从单个或多个传感器信息源获取的数据和信息进行关联、相关和综合，从而对态势和威胁及其重要程度进行全面及时评估的信息处理过程[3]。广义上，融合就是将来自多信息源的信息和数据进行综合处理，从而得出更为准确可靠的结论[4]。D-S证据理论、Bayes方法、模糊测度积分和专家系统等均是基于信息融合的可靠性评估技术中的常见方法。其中，D-S证据理论因其可以灵活处理不同可靠性数据和信息的形式差异，并具有直接表达不确定未知信息的能力，受到越来越多的重视和应用。

D-S证据理论是一种基于“证据”和“组合”来处理不确定性推理问题的数学方法[5]，已被尝试应用于故障诊断和健康管理的相关领域[6-7]。譬如，文献[8]研究了基于D-S证据理论的旋转机械综合故障诊断方法；文献[9]将证据理论与神经网络相结合，旨在解决航空发动机试车台试验中发动机磨损的故障诊断问题；文献[10]将D-S数据融合技术应用于多Agent的卫星故障诊断中，提高了诊断的准确性和多Agent系统的智能性；文献[11]提出一种基于粗糙集理论和D-S证据理论的设备技术状态评估模型。

针对航天设备的多源寿命信息，本文将D-S证据理论和Bayes理论相互结合，提出一种基于多源信息融合的寿命预测方法。首先，针对所研究的对象收集多种来源的寿命信息，包括专家经验、性能退化数据、相关(或相似)设备的寿命信息等；其次，将这些可靠性信息作为寿命预测的验前信息，挖掘其内外部信息，构建证据集合；最后，运用D-S证据合成规则对多证据的基本概率分配(Basic Probability Assignment，BPA)进行合成，将合成后的BPA作为各验前分布的融合权重分配结果，最终计算研究对象剩余寿命的验后分布曲线。仿真试验结果表明了本文方法的可行性和合理性。

1　D-S证据理论及Bayes可靠性评估

本文的主要目的是，将设备的多源寿命信息视作Bayes验前信息，且验前分布形式为威布尔分布，对分布中的尺度参数br进行基于D-S证据理论的融合估计求解。首先运用合成规则确定各验前信息的融合权重，得到尺度参数br的融合验前分布；再根据Bayes理论计算参数的验后分布估计值，并用估计值确定设备寿命的威布尔分布函数，最终得到设备寿命的预测值。本节将简要介绍D-S证据合成规则和Bayes验前信息融合的基本思想。

1.1证据合成的基本概念

D-S合成规则反映的是多组证据联合作用的结果。给定几组同一识别框架下的基于不同证据的基本概率分配函数，如果这几个证据不是完全冲突的，那么就可以利用D-S合成规则，计算出多证据联合作用下的基本概率分配函数[13]。

(1)

在基于信息融合的航天设备寿命预测问题中，焦元A1,A2，…,Ai和B1,B2，…,Bj代表多个寿命信息来源，m(C)是指经多个证据合成后分配到各信息源上的基本可信数。

1.2Bayes验前信息融合

本文选用威布尔分布作为航天设备剩余寿命的分布函数，因为它是航空航天设备常用的一种失效分布，尤其适用于机电类产品磨损累计失效的分布描述[14]。

假设设备的剩余寿命T服从威布尔分布

(2)

(3)

式中：Γ(•)为伽马函数；Q′(br)为Q(br)的一阶导数；αi和βi为参数，i表示第i个信息源。

假定现有k个关于尺度参数br的验前信息源，验前分布分别为πi(br)(i=1,2,…,k)，若得到各信息源的权重wi，则融合后br的验前分布为π(br)=wiπi(br)；另外假定通过现场试验已获得该设备的n个寿命数据，即真实寿命信息的集合，记为T={T1，T2,…,Tn}；由指数分布的共轭性质可以计算尺度参数br的验后分布

(4)

进而，根据最小方差估计原理可以求出尺度参数br的最小方差估计值

(5)

后文中将应用D-S证据理论中的基本概率分配和证据合成，确定各信息源的权重wi；与其他权重确定算法相比，本文方法可以统一处理形式各异的各类寿命信息，使得权重确定过程更加合理、准确。

2　基于D-S证据理论的寿命信息　 融合方法

由于航天设备很难获得大样本数据，本文将充分挖掘专家经验、遥测性能参数、相似系统寿命数据等验前信息，形成有关设备寿命的证据集合，运用D-S证据合成规则进行多个证据的BPA合成，作为各验前分布的融合权重分配，并利用权重得出验前分布融合结果，结合现场真实分布信息，最终计算得出研究对象寿命的Bayes验后分布曲线，具体实现流程如图1所示。

图1　D-S方法流程Fig.1　Flowchart of D-S method

2.1验前分布的信息挖掘及证据构成

本文将设备寿命信息划分为内部信息和外部信息[14]。内部信息是指设备寿命数据本身提供的信息，如数据容量、分布特征度；外部信息是寿命数据采集过程中的一些影响因素，如数据采集方法和水平、数据处理精度及信息来源的可信度。

(1)内部信息证据

不同来源寿命信息所包含的数据量大小存在明显差异，而数据量大小是影响数据驱动预测方法性能的主要因素，因此第一个D-S证据由数据容量特性构成。本文采用计算各信息源数据量的百分比作为数据容量基本概率分配(BPA)函数m1的构造方法。譬如，某设备有4种寿命信息源S1～S4，数据容量分别为130、400、255和140，则通过计算各容量占总容量的百分比可得数据容量证据E1的BPA结果为

E1={m1(S1)=0.141,m1(S2)=0.432,

m1(S3)=0.276,m1(S4)=0.151}

除了数据容量，不同寿命信息源的验前分布参数与现场真实分布参数之间的差异，也可度量该信息源的融合权重大小，因此第二个D-S证据为参数分布证据E2某设备4种信息源S1～S4的寿命分布参数θ的验前分布分别为π1(θ)=guass(4.9,1)，π2(θ)=guass(5.2,1)，π3(θ)=guass(4.2,1)，π4(θ)=guass(4.5,1)，均服从高斯分布；假定由现场试验数据得到的θ真实分布为π(θ)=guass(5,1)，下面来推导E2的BPA函数m2。

(6)

(2)外部信息证据

不同信息来源的寿命数据一般有着不同的采集方法和技术水平、数据处理的精度也不尽相同。此外，不同的信息来源也具有不同的可信度，这些外部信息也应当作为证据纳入D-S证据理论的证据合成中。

例如，文献[14]在分析某型柴油机的累积失效率和故障里程数之间的关系时，4种来源的故障里程数信息在数据质量、预处理方法和传感器精度等方面存在差异，经过数位专家的评估分析后，对信息源S1～S4赋予了不同的可信度，分别为0.995、0.987、0.926和0.912，该论文中得到的基于外部信息的可信度证据E3的BPA函数m3结果为

E3={m3(S1)=0.260 5,m3(S2)=0.258 4,

m3(S3)=0.242 4,m3(S4)=0.238 7}

同理，若获得了其他可量化的外部信息，也可以根据实际情况转化为融合权重分配这同一框架下的相应证据集合，加入影响信息源验前分布融合权重的考虑因素中。

2.2D-S证据理论融合过程模型

利用证据理论的合成规则(即式(1))，对第2.1节所提出的多组证据集合进行融合，可得到各信息源验前分布的权重分配集合。基于内部信息的各组证据的BPA融合形式为Wj=E1⊕E2,j，其中E2是分k个区间依次求解得到的，故E2有k个值。

由第1.1节可知，证据合成的次序对最终结果没有影响。若仍需继续考虑其他内外部信息的证据集合，权重计算公式可以扩展为通用形式

(7)

并利用得到的权重分配矩阵Wj(k×n)，其中，k表示求取参数分布证据E2时所划分的区间数，n表示验前信息来源的个数。结合式(3)，可得到k组融合验前分布πj(br)的集合

(8)

总结上述步骤，基于D-S证据理论的寿命信息融合过程如图2所示。其中，n表示证据数目，t表示信息源数目，mj(Si)表示在同一证据Ej的基本概率分配下的第i个信息源的基本可信数，i=1,2,…,t，j=1,2,…,n。通过D-S合成规则，各证据下的BPA函数mj进行合成，得到证据组合后的基本可信数m(Si)，即为组合后的各信息源置信度大小。进一步将置信度作为融合权重，至此，最终得到各信息源的验前融合权重Wi。

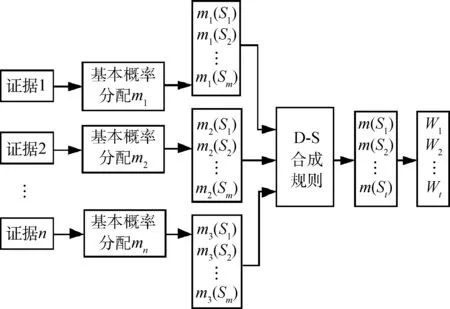
图2　基于D-S证据理论的融合过程模型Fig.2　Fusion process model based on D-S evidence theory

3　算法验证及分析

动量轮是卫星三轴稳定控制系统中的主要执行部件，动量轮的寿命直接影响卫星的使用寿命，实现动量轮剩余寿命的准确预测，对提高卫星可靠性进而延长卫星使用寿命具有重要意义[15]。

本文以XX型动量轮为研究对象，采用文献[16]中挖掘到的3种信息源S1～S3的验前分布信息和一组现场试验寿命数据分布信息，进行基于D-S证据理论的寿命信息融合方法的仿真验证。这里选择威布尔分布作为动量轮剩余寿命的分布形式，对尺度参数br的估计值进行融合求解。其中，3种来源的验前信息分别为相似型号动量轮的寿命数据、基于在轨温度性能的遥测数据推导得出的伪寿命数据、基于专家经验的寿命分布参数的区间估计。

3.1验前寿命信息挖掘

表1　现场真实分布及各验前分布参数表

图3　尺度参数各验前分布的概率密度曲线Fig.3　Prior distributions curves of scale parameter

3.2证据构成及融合

已知3种来源S1～S3的验前信息的原始数据量分别为13、5和10，通过计算各信息源数据量的百分比，得到数据容量证据E1的BPA，结果如表2示。可得

E1={m1(S1)=0.4643,

8m1(S2)=0.1786,m1(S3)=0.3571}

表2　信息源数据容量特征表

为了分析各信息源和现场试验尺度参数的分布情况，对πi(br)取积分，得到尺度参数br的累积分布函数，为了获得精确的参数分布证据E2的BPA，本文将时间轴0～800(月)划分成20个区间，确定各信息源在每个区间内的特征样本点及分布情况，如图4所示。

图4　尺度参数样本分布Fig.4　Samples distribution of scale parameter

这样，从尺度参数br累积概率的分布情况中统计得到特征样本点的数值大小，并进行接下来的分析。各信息源S1～S3和现场试验S0的特征样本点的数值和区间划分如表3所示。

分别计算第i个信息源在第j个区间内的样本点Pi,j与现场真实分布的样本点P0,j之间的距离L=|Pi,j- P0,j|，接着根据式(6)构建出各区间内的参数分布证据BPA,构建的20组BPA集合，如表4所示。

根据第2.2节所示方法及D-S证据理论合成规则，可以对数据容量证据E1和参数分布证据E2,j进行融合(j=1,2,…,20)。

表3　尺度参数样本点累积概率表

由于目前没有挖掘到更多的外部信息量，假设所有的信息源数据都采用统一的方法进行收集，并且在收集过程中有相同的技术水平，数据预处理精度一致，收集的数据有相同的可信度，这表明除了验前分布本身的内部信息之外并没有其他的外部信息应该在权重分配过程中考虑。所以，E1和E2,j经过证据合成后的BPA即为各信息源验前分布的权重集合，即Wj=E1⊕E2,j。权重分配结果如表5所示。

进一步地，可以根据表6结合各验前分布πi(br)计算得到融合后的尺度参数br的累积概率分布曲线，如图5所示。由图观察可知，融合后的参数累积概率分布与其他各单一信息来源的验前分布相比，更接近于现场真实分布。在认定现场数据最能反映产品真实信息的前提下，认为融合后的尺度参数br的累积概率分布曲线是合理的。

表4　参数分布证据BPA表

为了验证经过D-S证据组合后的权重分配结果更加合理，分别使用数据容量证据E1和参数分布证据E2这两类单一证据BPA作为验前分布的融合权重的分配结果，即分别用m1和m2直接表示Wj。计算由这两种单一证据所决定的权重分配，在各区间内融合后的特征样本点与现场数据样本点之间的距离，进行比较分析，结果如图6所示。

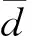
表5　验前分布权重分配向量

图5　融合后的尺度参数累积概率分布曲线Fig.5　Cumulative probability distribution curve of scale parameter after fusion

图6　三种融合样本点分布距离比较Fig.6　Distances comparison of three types fusiondistribution samples

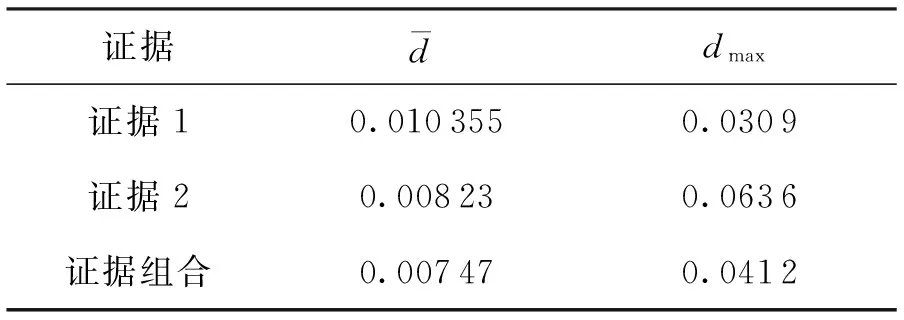
证据ddmax证据10.0103550.0309证据20.008230.0636证据组合0.007470.0412

3.3基于D-S证据合成的动量轮剩余寿命估计

根据第3.2节得到的各信息源验前分布的融合权重向量集合Wj，利用式(4)和式(7)，可以得到动量轮剩余寿命的尺度参数br的验后概率密度

经判定，该评估结果和工程实际相符合。由此可见，本文提出的基于D-S证据理论的验前分布融合权重分配的方法可行，可以解决工程实际问题。该方法改进了文献[16]考量验前分布相似性的基于JS距离的权重确定方法，充分挖掘了各验前信息源的内外部信息，并建立相应的证据和证据的基本概率分配函数，加入到证据合成的过程中，使得各信息源的权重分配更加合理准确。

图7　动量轮剩余寿命分布曲线Fig.7　Residual life distribution curve of momentum wheel

4　结束语

本文采用D-S证据合成方法来研究动量轮剩余寿命的验前分布融合问题，充分挖掘了各验前信息源的内、外部信息，构建了基于各类信息的D-S证据基本概率分配函数，并利用合成规则对多证据BPA进行合成，最终得到合理的各信息源的权重分配结果。

与现有研究方法相比，本文主要创新性在于，融合权重的确定不仅仅依据各信息源数据本身的特性，而是通过挖掘多种信息，构成D-S证据集合，再利用证据合成规则，来确定的权重分配结果。在对XX型动量轮的可靠性评估和剩余寿命预测过程中，针对多信息源所挖掘到的信息，构建了数据容量证据E1和参数分布证据E2的基本概率分配函数，通过两类证据的BPA的合成，得到各验前分布的权重分配并计算得出尺度参数br的最小方差估计值及估计区间。结果表明，通过本文方法获得的动量轮剩余寿命的威布尔分布符合实际工程经验，可以解决工程实际问题。

由于没有挖掘到XX型动量轮3种信息源的更多的外部信息量，本文假设所有的信息源数据都采用统一的收集方法进行收集，并具有相同的技术水平，数据预处理方式一致，信息来源具有相同的可信度。实际上，若存在可量化的外部信息，也应作为证据纳入对权重分配的考虑中。因此，本文后续工作还应探究外部信息的挖掘和证据的构建方法，使得权重的分配更加有据合理，剩余寿命的评估结果更加真实可信。

References)

[1]YE X, MA Y, MENG H, et al. Degradation failure model of electromagnetic relay[C]∥Proceeding of ICEC-ICREPEC 2012.Beijing, 2012: 116-123.

[2]邵瑞芝, 范本尧. 长寿命通信卫星的可靠性研究[J]. 中国空间科学技术, 1996, 16(4):24-33.

SHAO R Z, FAN BY. Reliability study of long-life communication satellites[J]. Chinese Space Science and Technology, 1996, 16(4):24-33(in Chinese).

[3]方艮海. 产品可靠性评估中的多源信息融合技术研究[D].合肥：合肥工业大学，2006.

FANG G H. Research on the multi-source information fusion techniques in the process of reliability assessment[D]. Hefei:Hefei University of Technology, 2006(in Chinese).

[4]庄钊文, 郁文贤, 王浩,等. 信息融合技术在可靠性评估中的应用[J]. 系统工程与电子技术, 1999, 22(4):6-9.

ZHUANG Z W, YU W X, WANG H, et al. Information fusion and application in reliability assessment[J]. Systems Engineering and Electronics, 1999, 22(4):6-9(in Chinese).

[5]SHAFER G. Perspectives on the theory and practice of belief functions[J]. International Journal of Approximate Reasoning, 1990, 4(5-6): 323-362.

[6]BAE H R, GRANDHI R V, CANFIELD R A. An approximation approach for uncertainty quantification using evidence theory[J]. Reliability Engineering and System Safety, 2004, 85(1-3): 215-225.

[7]AGARWAL H, RENAUD J E, PRESTON E L, et al. Uncertainty quantification using evidence theory in multidisciplinary design optimization[J]. Reliability Engineering and System Safety, 2004, 85(1-3): 281-294.

[8]高洪涛, 王敏. 证据理论在旋转机械综合故障诊断中的应用[J]. 大连理工大学学报. 2001, 41(4): 459-462.

GAO H T, WANG M . Application of D-S evidential reasoning to the comprehensive fault diagnosis of rotating machine[J]. Journal of Dalian University of Technology, 2001, 41(4): 459-462(in Chinese).

[9]陈果. 基于神经网络和D-S证据理论的发动机磨损故障融合诊断[J]. 航空动力学报, 2005, 20(2): 303-308.

CHEN G. Fusion diagnosis of engine wearing fault based on neural network and D-S evidence theory[J]. Journal of Aerospace Power, 2005, 20(2): 303-308(in Chinese).

[10]范显峰, 姜兴渭. 基于多Agent的卫星故障诊断融合技术研究[J]. 中国空间科学技术, 2003, 23(2):39-44.

FAN X F, JIANG X W. Research of multi-agent based satellite fault diagnosis and fusion technology[J]. Chinese Space Science and Technology, 2003, 23(2): 303-308(in Chinese).

[11]耿俊豹, 邱玮, 孔祥纯,等. 基于粗糙集和D-S证据理论的设备技术状态评估[J]. 系统工程与电子技术, 2008, 30(1): 112-115.

GENG J B, QIU W, KONG X C, et al. Techical condition evaluation for devices based on rough set theory and D-S evidence theory[J]. Systems Engineering and Electronics, 2008, 30(1): 112-115(in Chinese).

[12]ZHU P, XIONG W, QIN N, et al. D-S theory based on an improved PSO for data fusion[J]. Journal of Networks, 2012, 7(2):369-376.

[13]董彦民, 贺小帆, 刘文珽. 基于不同寿命分布的DFR值换算关系[J]. 北京航空航天大学学报, 2011, 37(12): 1524-1528.

DONG Y M, HE X F, LIU W T. Conversion relation of detail fatigue rating based on different fatigue life distribution[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(12): 1524-1528(in Chinese).

[14]孙锐. 基于D-S证据理论的信息融合及在可靠性数据处理中的应用研究[D]. 成都：电子科技大学, 2012.

SUN R. Research on D-S evidence theory based information fusion and its application in reliability data processing[D]. Chengdu:University of Electronic Science and Technology of China, 2012(in Chinese).

[15]JIN G, MATTHEWS D, FAN Y, et al. Physics of failure-based degradation modeling and lifetime prediction of the momentum wheel in a dynamic covariate environment[J]. Engineering Failure Analysis, 2013, 28(3):222-240.

[16]刘强. 基于失效物理的性能可靠性技术及应用研究[D].长沙：国防科学技术大学, 2011.

LIU Q. Research on the performance reliability technology and the application based on physics of failure[D].Changsha:Nation University of Defense Technology, 2011(in Chinese).

(编辑：高珍)

Lifetime prediction of aerospace equipment based on D-S evidence theory

DING Rui1, LU Ningyun1,*, CHENG Yuehua2, JIANG Bin1, XING Yan3,4

1.College of Automation Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 211016, China 2.College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 211016, China 3.Beijing Institute of Control Engineering, Beijing 100191, China 4.State Key Laboratory of Space Intelligent Control, Beijing 100191, China

An information fusion method was proposed based on D-S evidence theory and Bayes theory for lifetime prediction of important aerospace equipment, momentum wheel. Firstly, multi-source life information were collected and mined to obtain the prior distribution of the momentum wheel′s lifetime, in order to build D-S evidence collections.Secondly, D-S combination rule was used to obtain reasonable weight allocation for prior distributions. After that, fusion posterior distribution was figured out and the values of life parameters were also estimated. Finally, according to parameters′ estimation, the lifetime prediction for momentum wheel was derived. Simulation result shows that the prediction using the proposed method is closer to the real lifetime measurements.

lifetime prediction; multi-source information fusion;D-S evidence theory; Bayes method; Momentum wheel

10.16708/j.cnki.1000-758X.2016.0044

2015-11-26；

2015-12-30；录用日期：2016-05-11；

时间：2016-07-1213:26:34

http:∥www.cnki.net/kcms/detail/11.1859.V.2016.0712.1326.001.html

国家自然科学基金(61374141，61203091)

丁瑞(1991-)，女，硕士研究生，dingrui504@163.com

陆宁云(1977-)，女，教授，博士生导师，luningyun@nuaa.edu.cn,主要研究方向为复杂系统数据驱动建模、故障诊断与预测的理论和应用

TB114

A

http:∥zgkj.cast.cn

引用格式：丁瑞,陆宁云,程月华,等.基于D-S证据理论的航天设备寿命预测方法[J].中国空间科学技术, 2016,36(4)：58-66.DINGR,LUNY,CHENGYH,etal.LifetimepredictionofaerospaceequipmentbasedonD-Sevidencetheory, 2016,36(4)：58-66(inChinese).