1,3-丁二烯热裂解的动力学计算与模型研究

杜鸟锋　甯红波　李泽荣　张其翼,*　李象远(四川大学空天科学与工程学院，成都60065；四川大学化学工程学院，成都60065；四川大学化学学院，成都60064)

1,3-丁二烯热裂解的动力学计算与模型研究

杜鸟锋1甯红波2李泽荣3,*张其翼2,*李象远2
(1四川大学空天科学与工程学院，成都610065；2四川大学化学工程学院，成都610065；3四川大学化学学院，成都610064)

1,3-丁二烯是碳氢燃料燃烧和裂解过程中生成的一种重要产物，也是形成多环芳烃(PAHs)的一种重要前驱体。目前，关于1,3-丁二烯燃烧实验以及机理的研究较多，但是其热裂解机理的研究较少。本文在B3LYP/CBSB7水平下对1,3-丁二烯裂解过程中相关反应的反应物、产物以及过渡态进行了几何结构优化和频率计算，并通过组合方法CBS-QB3计算得到了单点能和热力学参数。对于紧致过渡态的反应和无能垒反应，分别采用过渡态理论(TST)和可变反应坐标过渡态理论(VRC-TST)计算其高压极限条件下的反应速率常数。计算得到的反应速率常数与已有文献报导的结果吻合较好。通过量子化学计算，对Hidaka等人提出1,3-丁二烯的热裂解机理模型进行了更新和改进：更新后的机理模型包含45个物种和224步反应，并对更新后的机理模型进行了模拟验证。结果表明，更新的机理模型能更好地预测1,3-丁二烯激波管裂解实验过程中C2H2、1-丁烯-3-炔(C4H4)以及苯(C6H6)主要产物的浓度分布，为进一步完善核心机理(C0－C4)模型提供了可靠的热、动力学参数。

1,3-丁二烯；热裂解机理；速率常数；动力学模拟

doi:10.3866/PKU.WHXB201512071

1　引言

1,3-丁二烯(1,3-C4H6)是碳氢化合物燃烧和裂解过程中生成的一种重要产物。例如，姚通和钟北京1在研究正癸烷裂解的小规模动力学机理模型中考虑了产物1,3-C4H6的生成；Zeng等2在研究正癸烷氧化和裂解的实验以及动力学模拟过程中考虑了不同压强下1,3-C4H6的生成量。此外，1,3-C4H6是一种致癌物，会通过汽车发动机的排气装置、生物质的燃烧以及工业使用过程排放到大气中，对人类可能有遗传毒性3。同时，1,3-C4H6也是形成多环芳烃(PAHs)和积碳的一种重要前驱体，并且，其燃烧火焰比芳香烃火焰更容易形成积碳，甚至在中温气相中也会发生聚合反应4－6。

目前，关于1,3-C4H6的裂解和燃烧的相关实验以及动力学模拟已有大量研究。其中，Granata等7构建了一个半详细的1,3-C4H6燃烧机理，模拟了逆流式扩散火焰条件下1,3-C4H6的燃烧实验，预测了其燃烧过程中PAHs的形成，但是PAHs的模拟值比实验值要高一些；Dagaut和Cathonnet8在射流搅拌器(JSR)中研究了温度750－1200 K、压强105和106Pa以及化学计量比为0.25－2条件下1,3-C4H6的燃烧实验和动力学模拟，但其机理模型中却未考虑压强效应对于反应速率常数的影响。因此，模拟结果存在一定误差；Hidaka等9构建了一个包含43个物种和89个反应的1,3-C4H6热裂解机理模型，并对1,3-C4H6在压强1.36×105－2.17×105Pa条件下的激波管实验进行了模拟验证，但其裂解产物丙炔(pC3H4)、苯(C6H6)的模拟结果与实验结果相比误差较大。此外，该机理中相同类型反应的速率常数是根据反应类思想估计得到的，因此存在着一定的误差。另外，该机理中没有考虑压强效应对于反应速率常数的影响，燃烧和裂解过程中一类重要的化学活化反应10(如2C2H3=H+ nC4H5(CH2＝CH―CH＝CH∙)和2C2H3=H+iC4H5(CH2＝CH∙―CH＝CH))也没有考虑；Laskin等11构建了一个详细的1,3-C4H6燃烧机理模型，并用该机理模拟了不同条件下的热裂解和燃烧实验。但是Laskin等11的1,3-C4H6燃烧机理模型在预测Hidaka等9的激波管实验结果时，1-丁烯-3-炔(C4H4)和C6H6的预测浓度值存在较大偏差；Peukert等12构建了1,3-C4H6高温裂解的动力学模型，只有初始反应物消耗的模拟结果与实验结果符合较好，但无法详细描述1,3-C4H6裂解过程中其他主要产物的浓度分布。

综上所述，文献7,8,11,12提到的机理模型包含的反应类型不全面，比如化学活化反应10是最近裂解中比较重要的一类化学反应，但在上述文献中涉及较少。另外，上述文献中的反应大都是在单一或者低压条件下进行的，压强相关反应的速率常数也涉及较少。因此，需要进一步完善1,3-C4H6热裂解过程中相关重要化学反应的研究。本文的主要目的是采用高精度组合方法CBS-QB313以及过渡态理论(TST)，可变反应坐标过渡态理论(VRCTST)获得了重要反应的精确动力学参数，并将计算的结果更新到Hidaka等9提出的1,3-C4H6热裂解机理模型中。另外，将Miller和Klippenstein14用RRKM/ME理论计算的C3和C4势能面上的一些压强相关反应的速率常数和Xu等15用QRRK/MSC理论计算的C2和C3势能面上的一些压强相关反应的速率常数补充到Hidaka等9的热裂解机理模型中。最后，用更新的包含45个物种和224步反应的1,3-C4H6热裂解机理模型进行流动反应器以及激波管实验的动力学模拟。结果表明，更新的机理模型能更好地预测1,3-C4H6裂解过程中的C2H2、C4H4以及C6H6等产物的浓度分布。这为进一步完善核心机理(C0－C4)模型提供了可靠的热、动力学参数。

2　计算细节

2.1计算方法

所有的电子结构计算都是通过Gaussian 03程序包16完成的，对于反应物、产物、过渡态的几何结构优化以及频率计算是在B3LYP/CBSB717,18水平下完成的。通过频率分析，所有驻点都没有虚频而过渡态有且仅有一个虚频。在B3LYP/CBSB7水平下，对过渡态进行了内禀反应坐标(IRC)19扫描确认。稳定结构和过渡态的单点能是采用CBS-QB313计算得到。这种方法对于含有C/H/O的体系可以得到较精确的能量，误差在6.28 kJ∙mol－1左右20。物质的标准生成焓(ΔfH⊖(298 K)，kJ∙mol－1)是采用原子化焓的方法计算得到的，并且在0 K时标准生成焓实验值C为711.67 kJ∙mol－1，H为216.16 kJ∙mol－121。本文计算的1,3-C4H6热裂解机理中涉及的

2.2反应速率常数的计算

本文所有反应的速率常数都是采用Variflex软件24计算得到的。对于有紧致过渡态的反应，高压极限下的速率常数采用TST计算得到。而没有过渡态的无能垒反应，高压极限下的速率常数是采用VRC-TST计算得到的。压强相关的反应速率常数是采用RRKM/ME理论计算得到的。

对于有紧致过渡态的反应，高压极限下速率常数的计算公式如下：

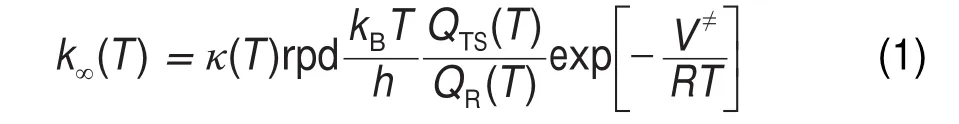
其中，κ(T)、rpd、kB和h分别是隧穿效应系数、反应路径的简并度、玻尔兹曼常数和普朗克常量。rpd是通过下式计算得到的：

其中，σTS和σR分别是过渡态和反应物的对称数，nTS和nR分别是过渡态和反应物的旋光异构体的数目。温度T的范围是500－2500 K，QR(T)是包含振动、转动、平动以及受阻转动的总摩尔配分函数，QTS(T)是过渡态的配分函数，V≠是包含零点能的活化能垒。

对于没有过渡态的无能垒反应，高压极限下的速率常数是采用VRC-TST计算得到的。其中，Morse公式E(R)=De{1－exp[－β(R－Re)]}2可以用来描述沿反应坐标变化的势能面能量。在这个方程中，De是不包含零点能的键能，而β=(fe/De)1/2，fe是最小势阱处键的力常数，R是反应坐标(两个成键原子之间的距离在本文中即C―C和C―H键的距离)，Re是R的平衡构型的键长。

根据RRKM理论，微观反应速率常数k(E,J)为：

其中，N(E,J)是过渡态从零到能量E和角动量J的态数目的总和，ρ(E,J)是在特定能量和角动量条件下反应物的态密度，N(E,J)和ρ(E,J)可以用Beyer-Swinehart算法25计算得到。

对于所有压强相关反应的速率常数计算，是通过RRKM理论与主方程结合得到。主方程可以用下面的矩阵方程形式来描述：

在上述方程中，∣w(t)>为描述粒子在t时刻各能级的分布向量，G为描述能级间能量转移速率与微观化学反应速率的矩阵。主方程的求解是基于特征值的求解方法26。所有主方程的计算都是在压强为103－107Pa下(以氩为载气)完成的。碰撞的能量转移速率的计算涉及碰撞频率和能量转移概率。本文能量转移概率模型采用指数降模型<△Edown>= 125(T/300)0.85,27碰撞频率计算常采用Lennard-Jones (L-J)势描写分子间相互作用。本研究中，载气氩的L-J参数σ=0.3542 nm，ε=64.8 cm－1来源于文献值28。而1,3-C4H6的L-J参数σ=0.5224 nm和ε= 227.3 cm－1是通过下面这两个经验公式29估计得到的：

其中，Tc是以K为单位的临界温度，Pc是以atm为单位的临界压强。

为了将反应速率常数直接应用于反应动力学模型中，本文将所有计算的反应速率常数在温度500－2500 K范围内拟合成三参数的修正Arrhenius公式形式：

本文主要计算了涉及1,3-C4H6的三种类型的反应，具体详见示意图1。

3　结果与讨论

3.1势能面

图1为本文计算的断键反应的势能图。根据自由基链式反应规则和分子的复杂程度，烃类化合物初始裂解可发生不同方式的C―C键或者C―H键断裂。1,3-C4H6有四个碳原子，根据分子的对称性，有两种C―C键断裂方式，分别是C1―C2和C2―C3键的断裂。由于在目前流行的碳氢化合物的燃烧机理中23,30,31，大多没有考虑1,3-C4H6中C1―C2键的断裂，因此本文也只研究了C2―C3键的断裂。C―H键断裂也有两种，C1原子上的C―H键断裂生成nC4H5和H，C2原子上的C―H键断裂生成iC4H5和H。因此，在图1中主要计算了1,3-C4H6的直接断键反应R1、R2以及R3(编号和对应的反应见示意图1)，其断键能分别为463.1、448.0、475.2 kJ∙mol－1，对于这三个反应Robinson等32给出了其断键能分别为466.8、458.0、489.9 kJ∙mol－1。可以看出，本文计算的结果与Robinson等32的结果吻合较好。图1中还给出了nC4H5自由基的β断键反应的能垒是163.7 kJ∙mol－1，与Dean33计算的该反应的能垒(169.1 kJ∙mol－1)吻合很好。

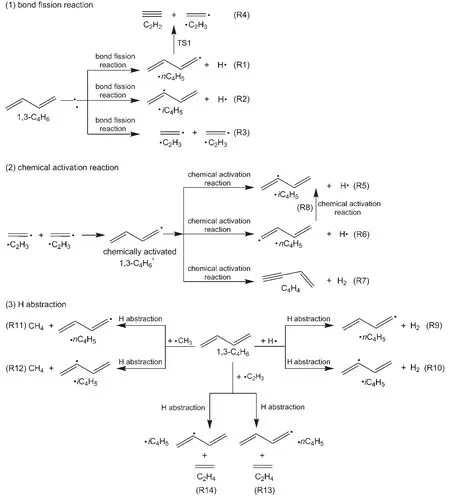
示意图1　涉及1,3-C4H6的三种反应类型Scheme 1　Three types of reaction involving 1,3-C4H6

图1也反映了本文计算的化学活化反应的势能图。在裂解过程中，以化学活化反应R5(C2H3+ C2H3=iC4H5+H)为例，其反应过程中，通过化学活化会形成处于高振动态的分子1,3-C4H6，该分子在高振动态时可直接生成iC4H5+H，也可与第三体碰撞得到稳定化的1,3-C4H6产物，二者是竞争反应，与压强有关。压强愈大，后者反应的竞争力愈强，前者反应速率愈小。故化学活化反应的速率常数随压强的增大而减小。同样，化学活化反应R6、R7以及R8也类似。

图2为本文计算的夺氢反应的势能图。该图给出了夺氢反应R9、R10、R11、R12、R13、R14的反应能垒，分别为62.0、51.1、68.7、59.0、43.1、33.5 kJ∙mol－1。从图中可以看出，从动力学和热力学的角度分析，1,3-C4H6的2位C上的氢均比端位C上的氢更易发生夺氢反应。

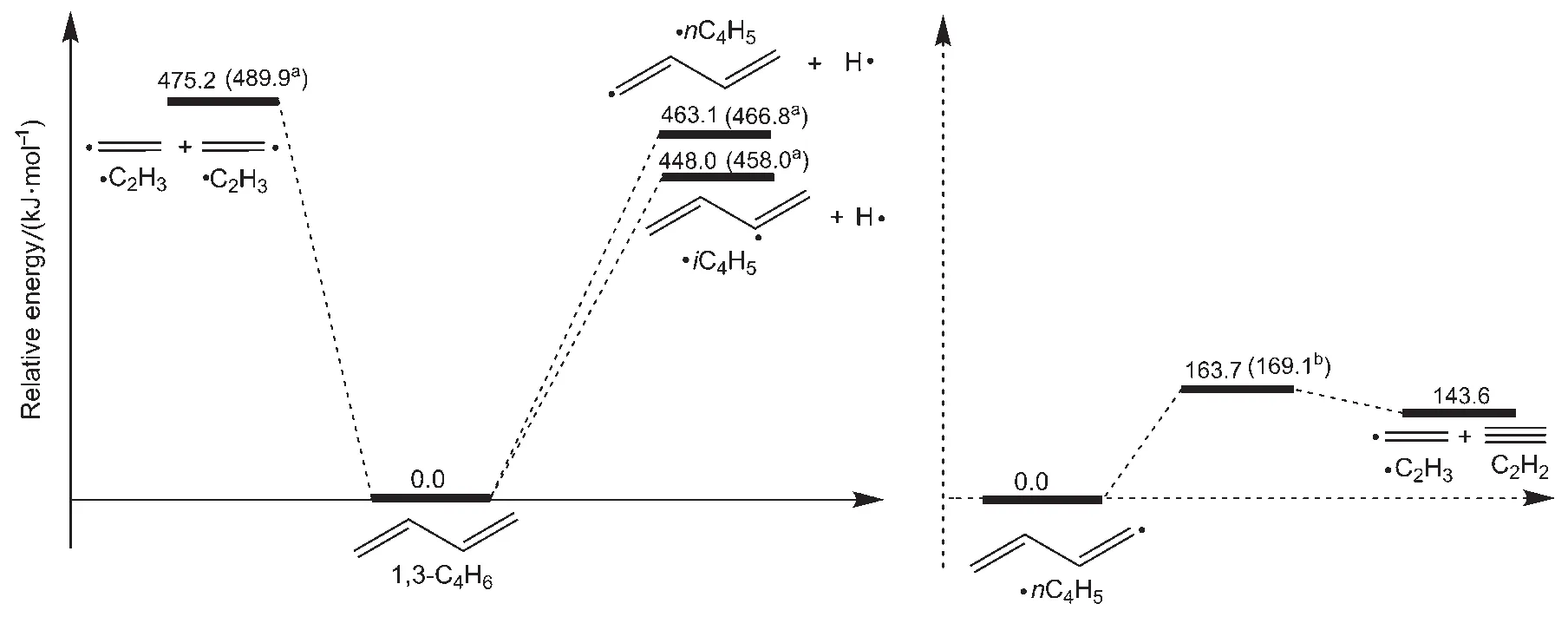
图1　在CBS-QB3水平下本文计算的断键反应的势能面(包含零点振动能)Fig.1　Potential energy profile for bond fission reactions calculated at level of CBS-QB3 (including zero-point vibrational energies)

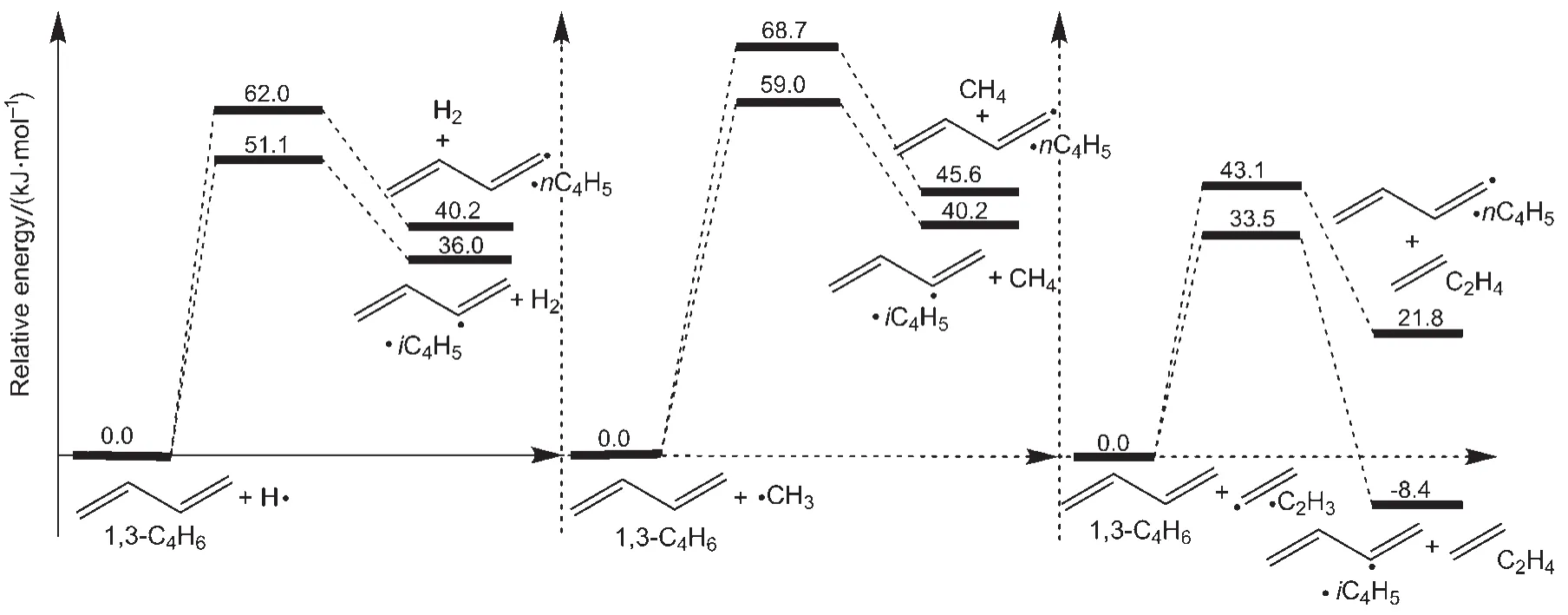
图2　在CBS-QB3水平下本文计算的夺氢反应的势能面(包含零点振动能)Fig.2　Potential energy profile for H-abstract reactions calculated at level of CBS-QB3 (including zero-point vibrational energies)

3.2动力学计算

3.2.1断键反应

3.2.1.1直接断键反应

对于无能垒的C―C和C―H键断裂反应，本文研究的反应包括反应R1、R2和R3。这些反应的高压极限速率常数本文采用VRC-TST理论计算得到。C―C键势能曲线是在B3LYP/CBSB7水平下以0.01 nm为间隔，距离R(C―C)从0.145－0.395 nm进行柔性扫描完成，对于C―H键的势能曲线也是在相同水平下以0.01 nm为间隔，距离R(C―H)从0.108－0.378 nm进行柔性扫描完成。然后，采用Morse势能公式E(R)=De{1－exp[－β(RRe)]}2拟合出计算反应速率常数需要的De和β。反应R1、R2和R3的Morse曲线均在Supporting Information的图S1中给出。最后，我们用Variflex软件24计算了这些反应的高压极限速率常数。本文计算的所有高压极限下的反应速率常数均在Supporting Information的表S2中给出。

直接断键反应的压强相关速率常数是采用RRKM/ME理论计算得到的，为了便于将计算的速率常数直接用于实际的模拟研究中，将计算结果拟合成修正的三参数Arrhenius公式形式。本文计算的所有压强相关反应的速率常数均在Supporting Information的表S2中给出。为了进一步说明压强对于直接断键反应速率常数的影响，反应R1、R2和R3不同压强下的反应速率常数随温度的变化在图3中给出。从图3中可以看出在500－1500 K范围内，压强对于反应速率常数的影响较小，在1500－2500 K范围内，压强对于反应的速率常数影响比较明显。因此，在低温段，压强对于其反应速率常数的影响较小；在高温段，压强对于其反应速率常数的影响较大。

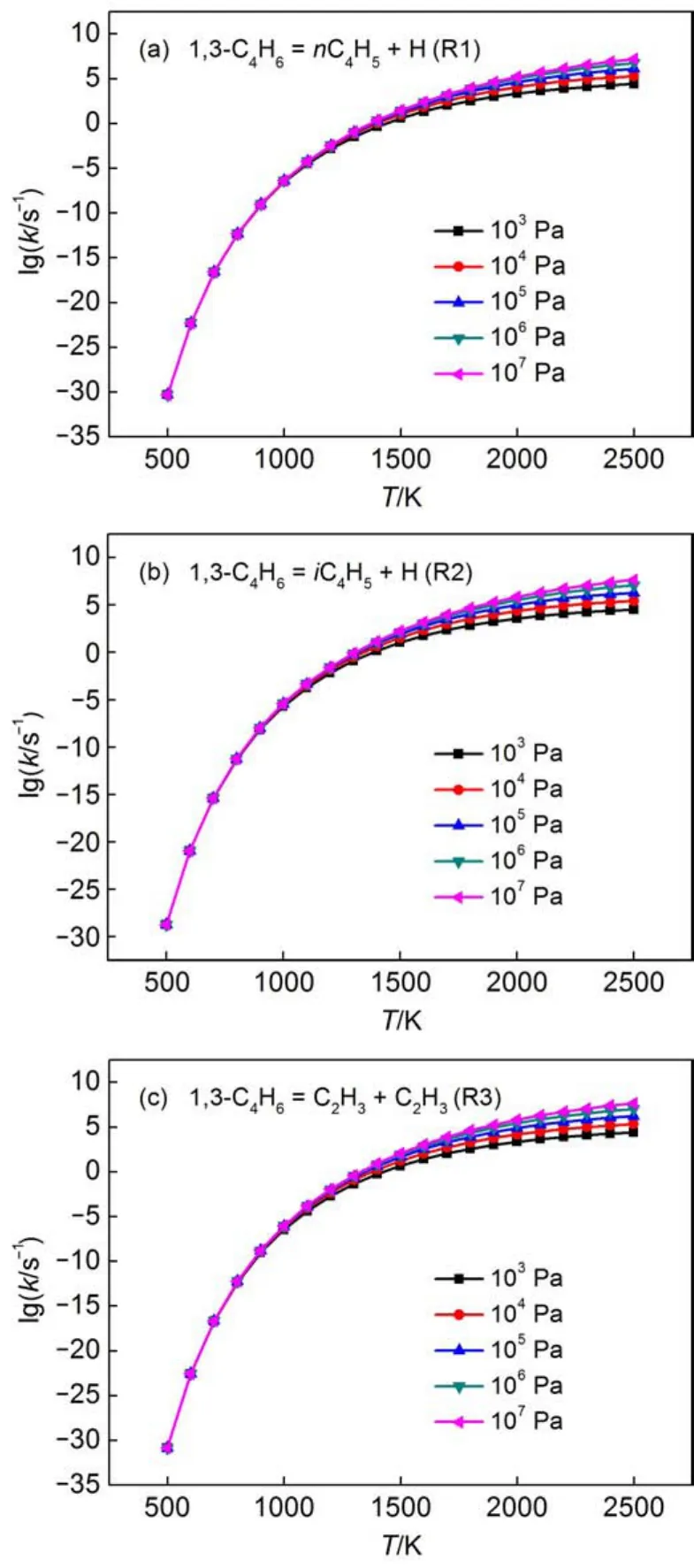
图3　压强对1,3-C4H6直接断键反应R1、R2和R3速率常数的影响Fig.3　Effect of pressure on the rate constants of the direct bond fission reactions R1,R2,and R3

在裂解和燃烧过程中，文献中报道了许多关于断键反应和结合反应的速率常数。其中，Wang等23用RRKM理论计算得到1,3-C4H6断键反应的速率常数；Hidaka等9用Dean33的理论推导出1,3-C4H6=iC4H5+H的反应速率常数。本文将压强为105Pa时计算得到的反应R1和R2的速率常数与Wang等23的结果进行对比，其结果在图4(a)和4(b)中给出；将压强为105Pa时计算得到的反应R3的速率常数与NIST22中报道的实验结果进行对比，其结果在图4(c)中给出。从图4(a－c)看出，本文计算的结果与文献结果吻合较好。其中反应R1的速率常数在温度为1500－2000 K时约是Wang等23结果的10倍，主要是本文采用RRKM/ME理论计算反应的速率常数，而Wang等23采用的是RRKM理论计算反应的速率常数。因此，本文计算得到的速率常数更准确；另外，反应R2的速率常数约是Wang等23结果的3倍；反应R3的速率常数约是NIST22中实验值的十分之一。

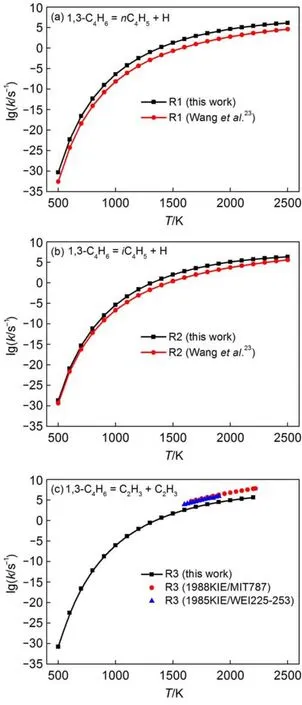
图4　(a)105Pa时本文计算的反应R1的速率常数与Wang等23结果的对比;(b)105Pa时本文计算的反应R2的速率常数与Wang等23结果的对比;(c)105Pa时本文计算的R3的速率常数与NIST22中的实验数据的对比Fig.4　(a)Comparison of our calculated rate constants at 105Pa for R1 with the results of Wang et al.23;(b) comparison of our calculated rate constants at 105Pa for R2 with the results of Wang et al.23;(c)comparisons of our calculated rate constant at 105Pa for R3 with experiment data of NIST22

3.2.1.2β断键反应

本文研究的β断键反应是烯基自由基β位C上的C―C键断裂形成小分子炔烃以及新自由基的反应。关于烯基自由基β断键反应的速率常数的研究大都是在高压极限的条件下，对于压强相关的速率常数的研究较少。Dean33采用QRRK理论方法计算得到了nC4H5自由基β断键反应的高压极限速率常数。图5(a)给出了压强对反应R4速率常数的影响，图5(b)给出了反应R4的高压极限速率常数与Dean33结果的对比。从图5(a)可看出，在低温段，压强对于反应速率常数的影响小；在高温段，压强对于反应速率常数的影响大。从图5(b)可看出，本文计算的反应R4的速率常数在500－1500 K时与Dean33的结果相差很大，主要是因为Dean33的结果是采用QRRK理论计算得到的，而本文的结果是采用RRKM/ME理论计算得到的。并且，Dean33在文章中也提到，计算断键反应的速率常数最好是采用RRKM理论，其精度要高于QRRK理论。因此，本文计算得到的速率常数可能更准确。

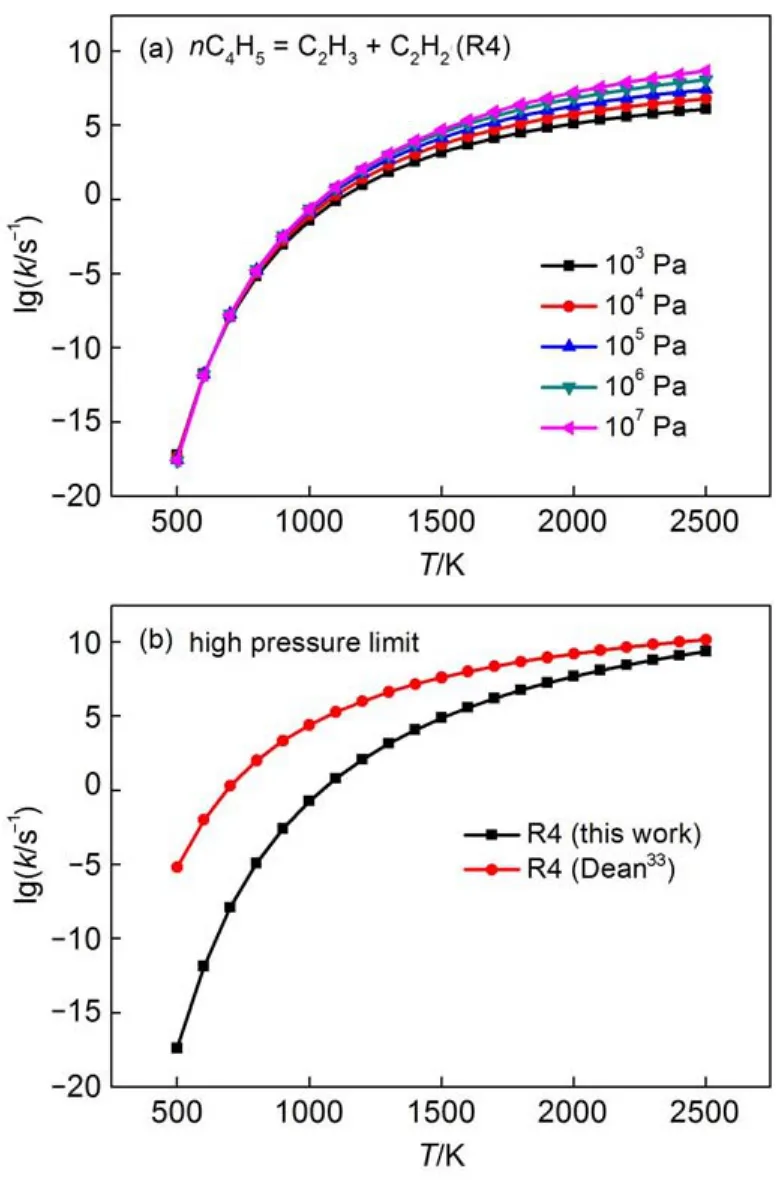
图5　(a)压强对β断键反应R4速率常数的影响；(b)反应R4高压极限下速率常数与Dean33结果的对比Fig.5　(a)Effect of pressure on the rate constants of β-scission reaction R4;(b)comparison of our calculated high-pressure limit rate constant for the β-scission reaction R4 with the result of Dean33

3.2.2化学活化反应

在高温条件下的燃烧或者裂解过程中，有许多活性片段存在，当这些活性片段结合的时候会形成高能振动的活化分子，这些活化分子一部分会转化为稳定的分子，另一部分会直接通过其他通道裂解，后者即为化学活化反应。这种反应类型是与压强相关的，并且反应速率随压强增大而减小。化学活化反应是所有碳氢化合物氧化和裂解过程中的一种重要反应类型，在动力学数据库中更不可或缺。因此，本文计算了1,3-C4H6热裂解机理模型中重要化学活化反应(包括R5－R8)的压强相关反应速率常数。其中，反应R5、R6、R7以及R8的压强相关反应速率常数随温度的变化均在Supporting Information的图S2中给出。

化学活化反应的反应活性较高，因此，一般实验比较难测得，可靠的实验数据较少。此外，理论计算也较少。其中，Wang等23计算了R5、R6以及R8压强相关的速率常数。图6(a－c)给出了压强为105Pa时反应R5、R6和R8的速率常数与Wang等23结果的对比。从图6(a－c)可以看出，R6的速率常数与Wang等23的结果吻合很好，而R5与R8的速率常数高出Wang等23的结果十倍左右。由于本文是采用RRKM/ME理论计算反应的速率常数，而Wang等23采用的是RRKM理论来计算反应的速率常数，因此本文计算的反应速率常数更准确。

3.2.3夺氢反应

由Kossiakoff和Rice34提出的自由基反应机理不能解释双分子反应过程，尤其是夺氢反应，因此，它也不能解释在高压条件下烷烃的生成。Fabuss等35提出，为了解释在高压条件下的产物分布，烷基和碳氢化合物的双分子反应必须考虑在内。在这些过程中，没有稳定的范德华复合物形成。因此，传统过渡态理论可以计算这种反应类型的速率常数。而且，这类反应是与压强无关的，速率常数仅与温度有关。

基于以上的讨论，较小的自由基可以夺取碳氢化合物中不同碳上的氢原子。本文主要计算了H、CH3以及C2H3自由基夺取1,3-C4H6中不同碳上氢原子的反应速率常数(包括反应R9－R14)。为了验证计算的夺氢反应速率常数的准确性，将本文的计算结果与Wang等23、Laskin等11、Hidaka等9、Dean33以及Wu和Kern36的结果进行了对比，其结果对比在图7和Supporting Information的图S3中给出。从图7和图S3中看出，其中反应R9、R10以及R11的速率常数与文献结果吻合较好。而反应R12的速率常数约是Wu和Kern36结果的十分之一，约是Laskin等11和Hidaka等9结果的五分之一，反应R13与R14的速率常数在低温段与Hidaka等8的结果差别较大。主要是因为Wu和Kern36、 Laskin等11以及Hidaka等9的反应速率常数是通过反应类思想估计得到的，因此结果存在一定误差；而本文的反应速率常数是采用TST理论计算得到的，故其结果更准确。

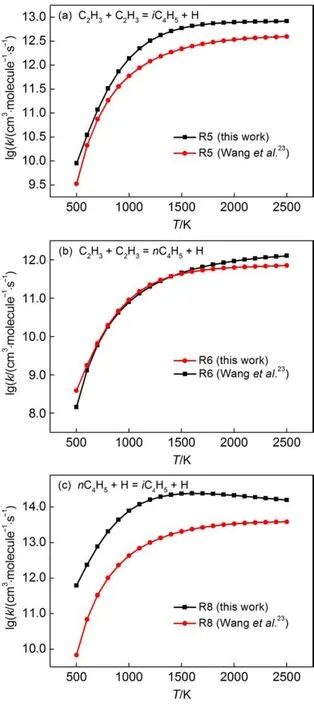
图6　在105Pa时本文计算的化学活化反应R5、R6和R8的速率常数分别与Wang等23结果的对比Fig.6　Comparisons of our calculated rate constants for reactions of R5,R6,and R8 with the results of Wang et al.23at 105Pa

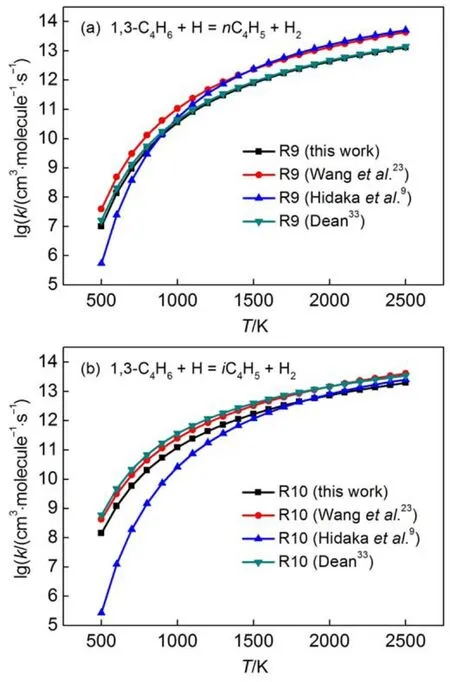
图7　(a)本文计算的反应R9高压极限下的速率常数与Wang等23,Hidaka等9以及Dean33结果的对比; (b)本文计算的反应R10高压极限下的速率常数与Wang等23,Hidaka等9以及Dean33结果的对比Fig.7　(a)Comparisons of our calculated high-pressure limit rate constant for reaction of R9 with the results of Wang et al.23,Hidaka et al.9,and Dean33;(b)comparisons of our calculated high-pressure limit rate constant for reaction of R10 with the results of Wang et al.23, Hidaka et al.9,and Dean33

3.3动力学模拟

3.3.1机理构建

本文采用高精度组合方法CBS-QB313以及TST，VRC-TST获得了重要反应的精确动力学参数，并将计算的结果更新到Hidaka等9提出的包含43个物种和89个反应的1,3-C4H6热裂解机理模型中。另外，将Miller等14用RRKM/ME理论计算的C3和C4势能面上的一些压强相关反应的速率常数和Xu等15用QRRK/MSC理论计算的C2和C3势能面上的一些压强相关反应的速率常数补充到Hidaka等9的热裂解机理模型中。最后，本文得到了一个包含45个物种和224步反应的详细1,3-C4H6热裂解机理模型。

3.3.2机理模拟

通过比较本文构建的1,3-C4H6热裂解机理的动力学模拟结果与Laskin等11的实验数据来验证本文机理的合理性。实验条件：裂解气组成3%(体积分数)1,3-C4H6和97%N2，实验温度分别为1110、1150以及1185 K，压强p=105Pa。模拟得到了上述条件下1,3-C4H6及其主要裂解产物的摩尔浓度随反应停留时间的分布。

图8和Supporting Information的图S4给出了实验测量以及动力学机理模拟的1,3-C4H6及其主要裂解产物的摩尔浓度随反应停留时间的变化。图8和图S4同时给出了本文热裂解机理模型以及Laskin等11机理模型的模拟结果。从图8(a)看出，本文机理模型中1,3-C4H6的消耗与实验结果吻合较好；从图8(b)看出，Laskin等11的机理模型对丙二烯(aC3H4)的预测值明显偏低，由于本文机理模型里面补充了一些C3势能面上的反应，因此，本文机理模型对aC3H4的模拟结果比Laskin等11机理模型的模拟结果准确。从图8和图S4中实验测量结果与本文机理模拟结果的对比可以看出，本文构建的1,3-C4H6的热裂解机理模型能够准确预测1,3-C4H6的消耗以及其主要裂解产物分布。

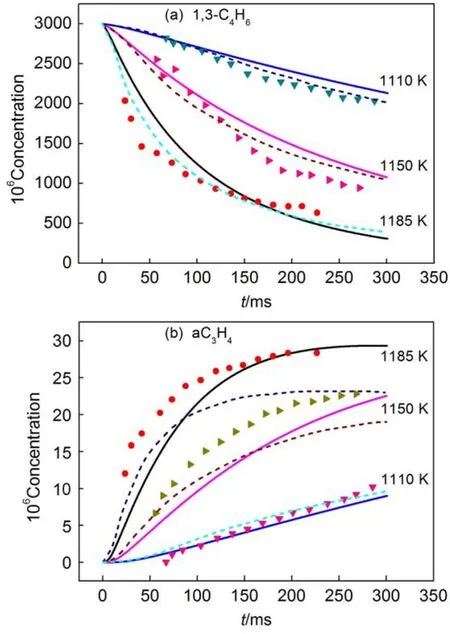
图8　裂解产物浓度实验与模拟结果的对比Fig.8　Comparison of the experimental and modeling results of the species concentrations

3.3.3激波管实验模拟

为了在较宽范围内验证本文构建的1,3-C4H6的热裂解机理能否较好的描述1,3-C4H6的裂解过程，采用零维均质反应模型对1,3-C4H6裂解过程进行动力学模拟。模拟条件如下：物种组成0.5%(体积分数)1,3-C4H6和99.5%Ar，T=1200－1600 K，p= 1.36×105－2.17×105Pa，反应时间t=1.3－2.4 ms。图9(a－d)给出了本文机理的模拟结果与Hidaka等9激波管实验结果的对比，同时也给出了Laskin等11机理模型的模拟结果。从图9(a－c)可以看出，本文机理在1200－1600 K温度范围内对1,3-C4H6、C2H2以及C4H4的模拟结果与实验值的平均误差分别为17.4%、60.4%以及18.3%，Laskin等11的机理模型对1,3-C4H6、C2H2以及C4H4的模拟结果与实验值的平均误差分别为30.2%、44.4%以及28.9%。整体上来说本文机理比Laskin等11的机理模型的模拟结果要好，但是本文机理和Laskin等11的机理模型对C2H2产量的预测与实验值的平均误差均较大；从图9(d)可以看出，本文机理模型对C6H6产量的预测与实验值吻合很好，而Laskin等11的机理模型对C6H6的预测值明显与实验结果偏差很大。

另外，本文计算的反应是C4势能面上的一些反应，为了验证本文计算的这些化学反应在1,3-C4H6热裂解机理中为关键反应，因此对C4H4以及1, 3-C4H6做了敏感度分析。在图10(a)和图10(b)中分别给出了温度T=1500 K、停留时间t=1.52 ms条件下激波管中1,3-C4H6热解转化率为20%处的对主要产物C4H4(仅考虑了敏感度系数大于0.08的反应)的产率以及初始物1,3-C4H6(仅考虑了敏感度系数大于0.002的反应)相对敏感度系数最大的10个基元反应。敏感度系数为正表示该反应速率常数的增加对产物产率有正的影响，敏感度系数为负则表示该反应速率常数的增加对产物产率有负的影响。

从图10(a)中看出，对C4H4产率敏感度系数最大的三个反应是1,3-C4H6的氢提取反应(R10)、乙烯基的C―H断键反应以及1,3-C4H6的C―H断键反应(R2)，其中两个反应(R2和R10)来自于本文计算的反应；从图10(b)中看出，对1,3-C4H6敏感度系数最大的10个反应中，其中三个反应(R1、R2和R3)来自于本文计算的反应。以上说明本文计算的这些化学反应在1,3-C4H6热裂解机理中为关键反应，对其裂解模拟结果有一定的改进作用，使该机理模型对实验结果的预测值更准确。

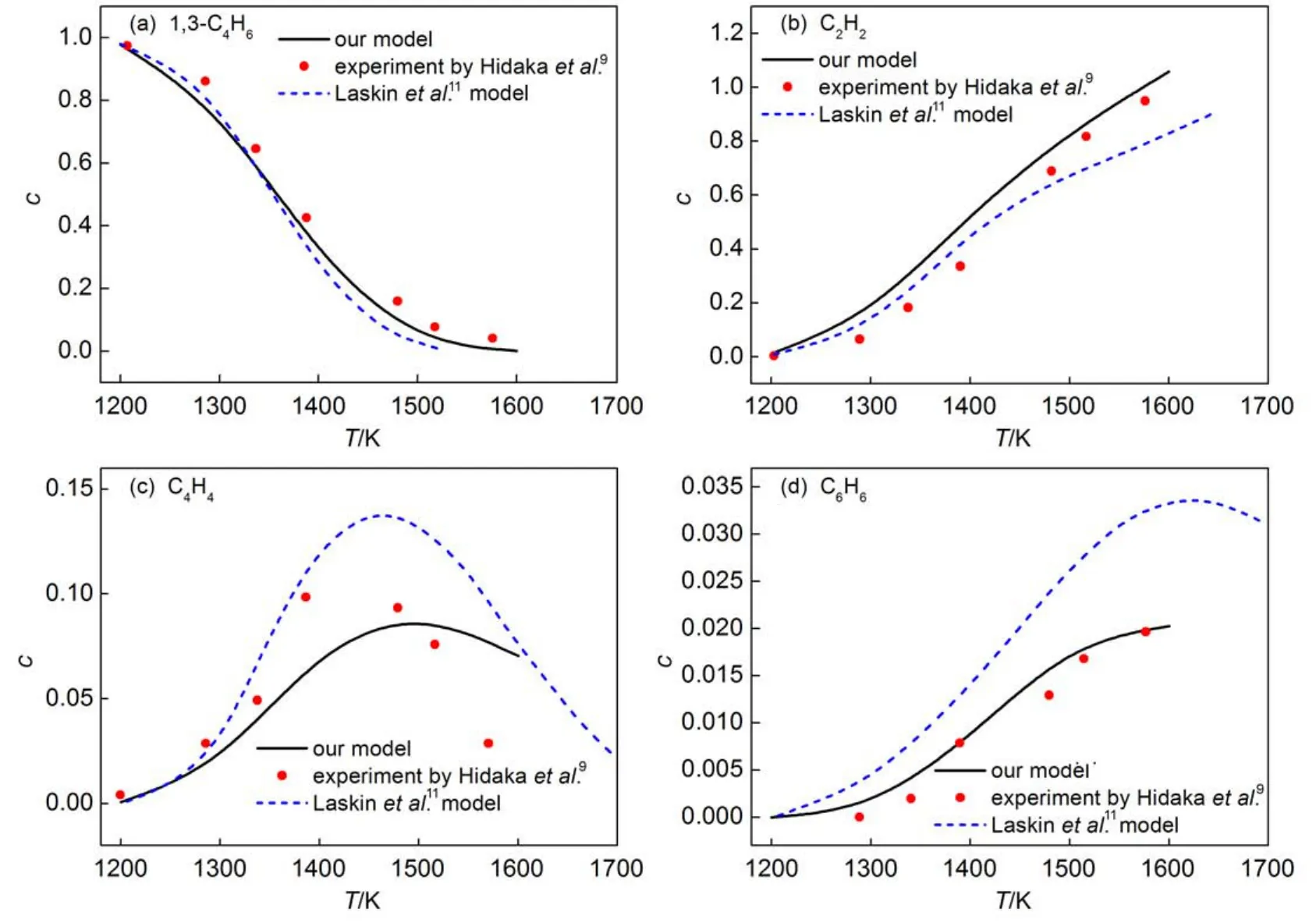
图9　1,3-C4H6裂解组分分布对比Fig.9　Comparison of the species profiles in 1,3-C4H6pyrolysis

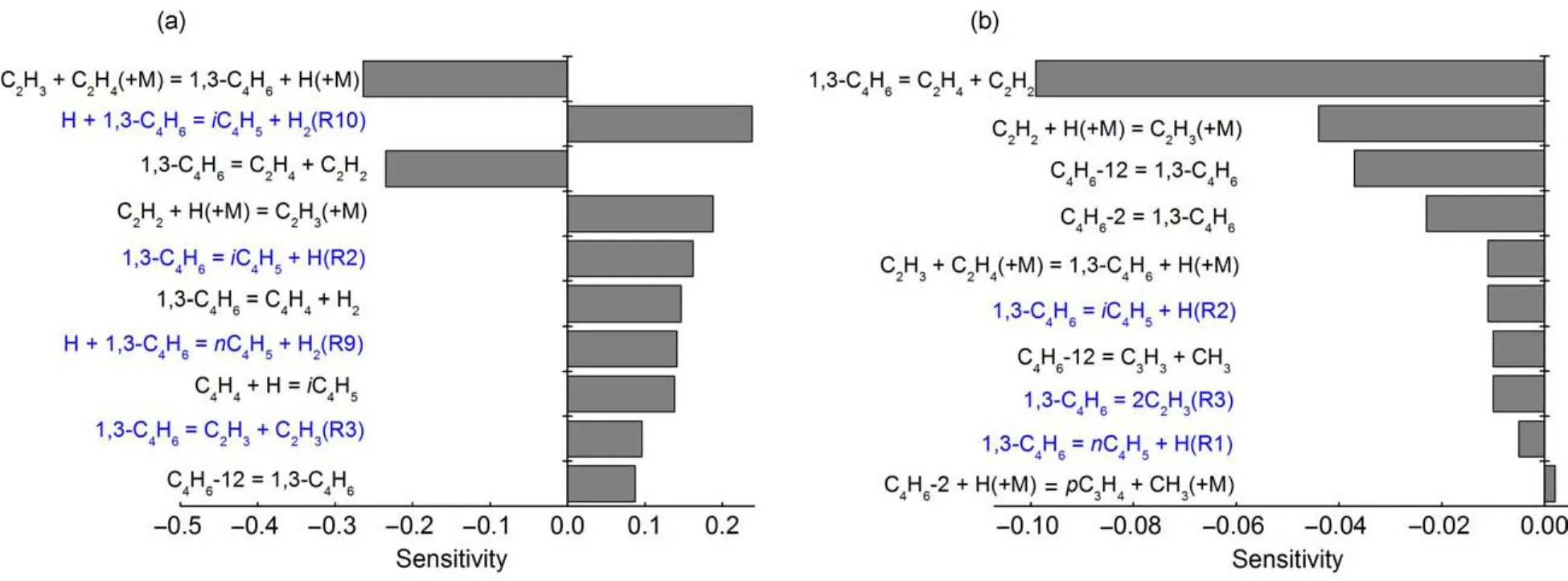
图10　(a)产物C4H4的敏感度系数;(b)初始反应物1,3-C4H6的敏感度系数Fig.10　(a)Sensitivity coefficient of the product C4H4;(b)sensitivity coefficient of the primary reactant 1,3-C4H6

综上所述，本文构建的1,3-C4H6热裂解机理模型对温度在1200－1600 K范围内的激波管实验的预测结果明显好于Laskin等11机理模型的预测结果，因为本文机理模型中的反应类型比Laskin等11机理模型中的反应类型要多，而且相关反应的速率常数也比Laskin等11机理模型中的反应速率常数准确。

4　结论

本文采用高精度的量子化学方法计算得到了重要反应的速率常数，并将计算的结果更新到Hidaka等9提出的1,3-C4H6热裂解机理模型中。另外，将Miller和Klippenstein14用RRKM/ME理论计算的C3和C4势能面上的一些压强相关反应的速率常数和Xu等15用QRRK/MSC理论计算的C2和C3势能面上的一些压强相关反应的速率常数补充到Hidaka等9的热裂解机理模型中。最后，重新构建了一个含有45个物种和224步反应的详细1,3-C4H6热裂解机理，构建的机理考虑了压强相关反应的速率常数。进一步，我们用本文构建的1,3-C4H6热裂解机理模型进行了平推流实验和激波管实验结果的预测。结果表明，该机理能够很好地描述1,3-C4H6的热裂解过程，准确预测其主要裂解产物分布。另外，在本文构建的1,3-C4H6热裂解机理模型的基础上通过敏感度分析，表明本文计算的一部分化学反应在1,3-C4H6热裂解机理中为关键反应，对其裂解模拟结果有一定的改进作用。

1,3-C4H6热裂解机理是碳氢化合物燃烧和裂解模型中核心机理(C0－C4)的重要组成部分。本文采用高精度的量子化学方法并结合RRKM/ME理论计算得到的这些反应的压强相关速率常数，为进一步完善核心机理(C0－C4)模型提供了可靠的热力学参数和动力学参数。

致谢：感谢深圳国家超级计算中心提供的软件资源。

Supporting Information:Table S1,Table S2,Fig.S1,Fig. S2,Fig.S3,and Fig.S4 have been included,the mechanism of 1, 3-butadiene pyrolysis has also been included.This information is available free of charge via the internet at http://www.whxb. pku.edu.cn.

References

(1)Yao,T.;Zhong,B.J.Acta Phys.-Chim.Sin.2013,29(7), 1385.[姚通,钟北京.物理化学学报,2013,29(7),1385.] doi:10.3866/PKU.WHXB201304123

(2)Zeng,M.R.;Yuan,W.H.;Wang,Y.Z.;Zhou,W.X.;Zhang,L. D.;Qi,F.;Li,Y.Y.Combust.Flame 2014,161,1701.doi: 10.1016/j.combustflame.2014.01.002

(3)Hughes,K.;Meek,M.E.;Walker,M.;Beauchamp,R.1,3-Butadiene:Human HealthAspects.In Concise International Chemical Assessment Document 30;WHO:Geneva, Switzerland,2001;pp 1－73.

(4)Vaughan,W.E.J.Am.Chem.Soc 1932,54,3863.doi:10.1021/ ja01349a008

(5)Kistiakovsky,G.B.;Ransom,W.W.J.Chem.Phys.1939,7, 725.doi:10.1063/1.1750519

(6)Harkness,J.B.;Kistiakowski,G.B.;Mears,W.H.J.Chem. Phys.1937,5,682.doi:10.1063/1.1750100

(7)Granata,S.;Faravelli,T.;Ranzi,E.;Olten,N.;Senkan,S. Combust.Flame 2002,131,273.doi:10.1016/S0010-2180(02) 00407-8

(8)Dagaut,P.;Cathonnet,M.Combust.Sci.Technol.1998,140, 225.doi:10.1080/00102209808915773

(9)Hidaka,Y.;Higashihara,T.;Ninomiya,N.;Masaoka,H.; Nakamura,T.;Kawano,H.Int.J.Chem.Kinet.1996,28,137.

(10)Tsang,W.ChemicalActivation Reactions in the Heptane Combustion Kinetics Database.InAIAA 44th Aerospace Sciences Meeting and Exihibt,American Institute of Aeronautics andAstronautics,Reno,Nevada,January 9－12, 2006.

(11)Laskin,A.;Wang,H.;Law,C.K.Int.J.Chem.Kinet.2000,32, 589.

(12)Peukert,S.;Braun-Unkhoff,M.;Naumann,C.High Temperature Kinetics of the Pyrolysis of 1,3-Butadiene and 2-Butyne.In Fundamental Physical and Chemical Kinetics, Proceedings of the European Combustion Meeting,Vienna, Austria,April 14－17,2009.

(13)Montgomery,J.A.,Jr.;Frisch,M.J.;Ochterski,J.W.; Petersson,G.A.J.Chem.Phys.1999,110,2822.doi:10.1063/ 1.477924

(14)Miller,J.A.;Klippenstein,S.J.J.Phys.Chem.A 2013,117, 2718.doi:10.1021/jp312712p

(15)Xu,C.;Shoaibi,A.S.A.;Wang,C.G.;Carstensen,H.H.; Dean,A.M.J.Phys.Chem.A 2011,115,10470.

(16)Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03,Revision B.05;Gaussian Inc.:Pittsburgh,PA,2003.

(17)Becke,A.D.J.Chem.Phys.1993,98,1372.doi:10.1063/ 1.464304

(18)Lee,C.;Yang,W.;Parr,R.G.Phys.Rev.B 1988,37,785.doi: 10.1103/PhysRevB.37.785

(19)Gonzalez,C.;Schlegel,H.B.J.Chem.Phys.1989,90,2154. doi:10.1063/1.456010

(20)Sirjean,B.;Fournet,R.J.Phys.Chem.A 2012,116,6675.doi: 10.1021/jp303680h

(21)Curtiss,L.A.;Raghavachari,K.;Redfern,P.C.;Pople,J.A. J.Chem.Phys.1997,106,1063.doi:10.1063/1.473182

(22)Gaithersburg,M.D.NIST Computational Chemistry Comparison and Benchmark Database;National Institute of Standards and Technology.http://webbook.nist.gov/chemistry (2003).

(23)Wang,H.;You,X.Q.;Joshi,A.V.;Davis,S.G.;Laskin,A.; Egolfopoulos,F.N.;Law,C.K.USC Mech Version II.High-Temperature Combustion Reaction Model of H2/CO/C1－C4Compounds.http://ignis.usc.edu/USC_Mech_II.htm(accessed 2007).

(24)Klippenstein,S.J.;Wagner,A.F.;Dunbar,R.C.;Wardlaw,D. M.;Robertson,S.H.VariFlex,Version 1.0;Argonne National Laboratory:Argonne,IL,1999.

(25)Beyer,T.;Swinehart,D.F.Comm.Assoc.Comput.Mach. 1973,16,379.

(26)Holbrook,K.A.;Pilling,M.J.;Robertson,S.H.,Unimolecular Reactions,2nd ed.;John Wiley&Sons: Chichester,UK,1996.

(27)Miller,J.A.;Klippenstein,S.J.J.Phys.Chem.A 2003,107, 2680.doi:10.1021/jp0221082

(28)Saito,K.;Kakumoto,T.;Murakami,I.J.Phys.Chem.1984, 88,1182.doi:10.1021/j150650a033

(29)Welty,J.R.;Wicks,C.E.;Wilson,R.E.;Rorrer,G.L., Fundamentals of Momentum,Heat and Mass Transfer,4th ed.; John Wiley&Sons Ltd.:New York,2001.

(30)Metcalfe,W.K.;Burke,S.M.;Ahmed,S.S.;Curran,H.J.Int. J.Chem.Kinet.2013,45,638.doi:10.1002/kin.2013.45.issue-10

(31)UCSD,The San Diego Mechanism,Version 20141004,2014. http://maeweb.ucsd.edu/combustion/.

(32)Robinson,J.C.;Harris,S.A.;Sun,W.;Sveum,N.E.; Neumark,D.M.J.Am.Chem.Soc.2002,124,10211.doi: 10.1021/ja0127281

(33)Dean,A.M.J.Phys.Chem.1985,89,4600.doi:10.1021/ j100267a038

(34)Kossiakoff,A.;Rice,F.O.J.Am.Chem.Soc.1943,65,590. doi:10.1021/ja01244a028

(35)Fabuss,B.M.;Borsanyi,A.S.;Satterfield,C.N.;Lait,R.I.; Smith,J.O.Ind.Eng.Chem.Process Des.Dev.1962,1,293. doi:10.1021/i260004a011

(36)Wu,C.H.;Kern,R.D.J.Phys.Chem.1987,91,6291.doi: 10.1021/j100308a042

Kinetic Calculation and Modeling Study of 1,3-Butadiene Pyrolysis

DU Niao-Feng1NING Hong-Bo2LI Ze-Rong3,*ZHANG Qi-Yi2,*LI Xiang-Yuan2
(1School of Aeronautics&Astronautics,Sichuan University,Chengdu 610065,P.R.China;2School of Chemical Engineering, Sichuan University,Chengdu 610065,P.R.China;3College of Chemistry,Sichuan University,Chengdu 610064,P.R.China)

1,3-Butadiene is an important product in combustion and pyrolysis of hydrocarbon fuels and it is also an important precursor to form polycyclic aromatic hydrocarbons(PAHs).Currently,a variety of experimental and mechanism studies have been performed on 1,3-butadiene oxidation.However,few studies about pyrolysis mechanism of 1,3-butadiene have been done.In this work,the optimization of the geometries and the vibrational frequencies for the reactants,products,and transition states of the relevant reactions in 1,3-butadiene pyrolysis have been performed at the B3LYP/CBSB7 level.Their single point energies and the thermodynamic parameters are also calculated by using the composite CBS-QB3 method.The high-pressure limit rate constants for tight transition state reactions and barrierless reactions are obtained by transition state theory and variable reaction coordinate transition state theory,respectively.The calculated rate constants in this work are in good agreement with those available from literature.Furthermore,the mechanism of Hidaka et al.is updated with replacing the calculated rate constants of reactions in this work to simulate the shock tube experiment results of 1,3-butadiene pyrolysisand the updated mechanism consists of 45 species and 224 reactions.It can be seen that the updated mechanism can improve the concentration profiles of the main products,ethylene,1-butylene-3-acetylene,and benzene in 1,3-butadiene pyrolysis.It can also provide reliable kinetic and thermodynamic parameters to further improve the core mechanism of C0－C4species.

August 24,2015;Revised:December 7,2015;Published on Web:December 7,2015.

1,3-Butadiene;Pyrolysis mechanism;Rate constant;Kinetic simulation重要反应物种的标准生成焓、熵以及热容在Supporting Information表S1中给出。从表S1中可以看出，计算的标准生成焓与国家标准与技术(NIST)数据库中的数据22吻合较好。更新的机理模型中其他物种的热力学数据来自Wang等23的核心机理。

O643

*Corresponding authors.LI Ze-Rong,Email:lizerong@scu.edu.cn.ZHANG Qi-Yi,Email:qyzhang@scu.edu.cn;Tel:+86-28-85406139.

The project was supported by the National Natural Science Foundation of China(91441114,91441132).

国家自然科学基金(91441114,91441132)资助项目

©Editorial office ofActa Physico-Chimica Sinica