基于切换模型的跳变负载下电机自适应控制

宗晓萍,崔恩畅,王霞,王培光

(河北大学 电子信息工程学院，河北 保定　071002)



基于切换模型的跳变负载下电机自适应控制

宗晓萍,崔恩畅,王霞,王培光

(河北大学 电子信息工程学院，河北 保定071002)

基于负载反复切换的电机模型设计了参考模型自适应跟踪控制器.首先，构建电机的切换系统数学模型，并将负载更替看作切换信号.其次，对切换系统进行自适应控制器设计，解决了负载切换后出现的误差瞬增问题，保证了系统的渐进跟踪.最后，给出仿真算例，验证所设计控制器的性能，并说明了切换信号对系统动态特性造成的影响.

跳变负载；切换系统；自适应控制；跟踪

电机是一种重要的执行机构，具有时变、非线性、强耦合的特点[1].实际应用中，电机往往需要在不同工况下带动不同的负载[2]，例如吊车里的电机要反复拉起或放下重物.负载的切换会使电机的转动惯量等参数发生突变，致使电机参数为未知且不断跳变的分段常量.若采用非切换系统模型和传统自适应控制方法，控制器参数在每次负载切换后，都要重新适应，造成误差瞬增，不能保证渐近的控制性能[3-5].

切换系统是一类特殊的混杂系统，由多个子系统和切换信号组成[6-7].最初，切换系统的概念是在数字化控制过程中多率采样数据系统的研究中提出的，可用于描述元件损坏造成结构突变的系统或因扰动含有突变参数的系统.如今，切换系统在控制领域具有广泛的实际应用背景：许多实际的物理系统，内在机理本身就是切换系统，如电力系统、混合动力系统等[8-9]；因负载切换等原因造成系统参数突变的系统也可以看作切换系统[10]；分段系统是一类按状态切换的特殊切换系统[11]；多控制器切换的系统，其闭环也为切换系统[12].

控制器的控制效果依赖于模型本身的精度，但在实际应用中，精确的模型是不存在的，很多系统会因外部扰动或者参数随环境变化而受到影响[13].如何设计控制器，使具有不确定性、未知性和时变性参数的系统满足控制要求，是非常重要的.自适应控制根据实际控制效果在线调节控制器参数，因此可以应对建模误差、环境变化甚至系统参数未知等不确定因素，达到控制的目的[14].

近年来，切换系统的自适应控制问题受到了越来越多的关注，并取得一定的研究成果.目前的研究主要集中在线性切换系统特别是能控标准型线性切换系统上，基于Lyapunov和无源框架给出任意切换和驻留时间下的设计方案[15-18].对于未知参数跳变的系统，将其看作切换系统来设计自适应控制器，能够在切换作用下保证系统的渐近控制性能.切换系统自适应控制的应用研究尚不多见，在机械臂的研究中稍有涉及[19-21].如何将切换系统的自适应控制方法应用到电机控制中，为切变负载的电机设计自适应控制器，尚未见报道.

本文将参数跳变的电机视为切换系统，建立含有线性不确定参数的切换电机模型，并针对该模型设计自适应控制器[22]，研究模型参考自适应跟踪问题，保证系统在任意负载切换下的渐近跟踪性能.实例仿真结果验证了该控制器的控制效果.

1　电机的切换模型及问题描述

本文以无刷直流电机(BLDCM)为例建立模型[23]，不计涡流和磁滞损耗，忽略齿槽、换相过程及电枢反应的影响[24].三相绕组的电压平衡方程为

(1)

其中Ua、Ub、Uc为电机三相绕组相电压；R为绕组电阻；ia、ib、ic为电机三相绕组相电流；Ls为三相绕组的自感，M为绕组间的互感；Ea、Eb、Ec为电动机三相绕组的反电动势.

忽略无刷电机绕组中因换相引起的电流波动及二极管压降和续流，将电机视作一个整体，则BLDCM的电压平衡方程为

(2)

其中，U为电机绕组端头电压,ra、La分别为电枢绕组的电阻和电感,ke为反电动势系数.

机械运动方程为

(3)

其中，Te为电磁转矩，TL为负载转矩，J为转动惯量，ωm为电机机械角速度，Bv为黏滞摩擦系数.

由式(1)-(3)及BLDCM原理，推导出BLDCM的二阶动力学模型，其中状态方程为[25]

(4)

对上述方程进行整理，得到状态空间模型的一般形式

(5)

其中，θ为系统中的不确定常数矩阵，B为输入增益矩阵，d(t)为系统的外部扰动.

由于负载不断切换，转动惯量以及负载惯量也随之变化，导致系统参数和外部扰动的不断跳变.因此将参数跳变的电机视为切换系统，研究其自适应跟踪问题.

具有不确定参数的非线性电机系统，其切换模型的一般形式为

(6)

其中，x∈Rl×n是系统的状态矢量，θ∈Rn×p为系统中的不确定常数矩阵，σ∈Λ={1,2,…,N}为切换信号，Bσ∈Rn×1为输入增益矩阵，u∈R是输入矢量，d(t)为系统的外部干扰.

本文的控制目标是为切换系统(6)设计自适应跟踪控制器，使其状态在任意负载切换下能够渐近跟踪参考状态xM，即对任意的切换信号σ有

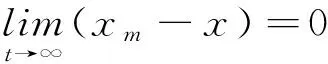
(7)

参考状态xM由如下的参考模型产生：

(8)

其中，AM∈Rn×n为稳定矩阵,BM∈Rn×i为增益矩阵.AM满足

AMTP+PAM=-Q,

(9)

其中，P、Q是正定对称矩阵,r∈R为有界输入.

2　自适应控制器的设计

自适应控制器的控制结构如图1所示.

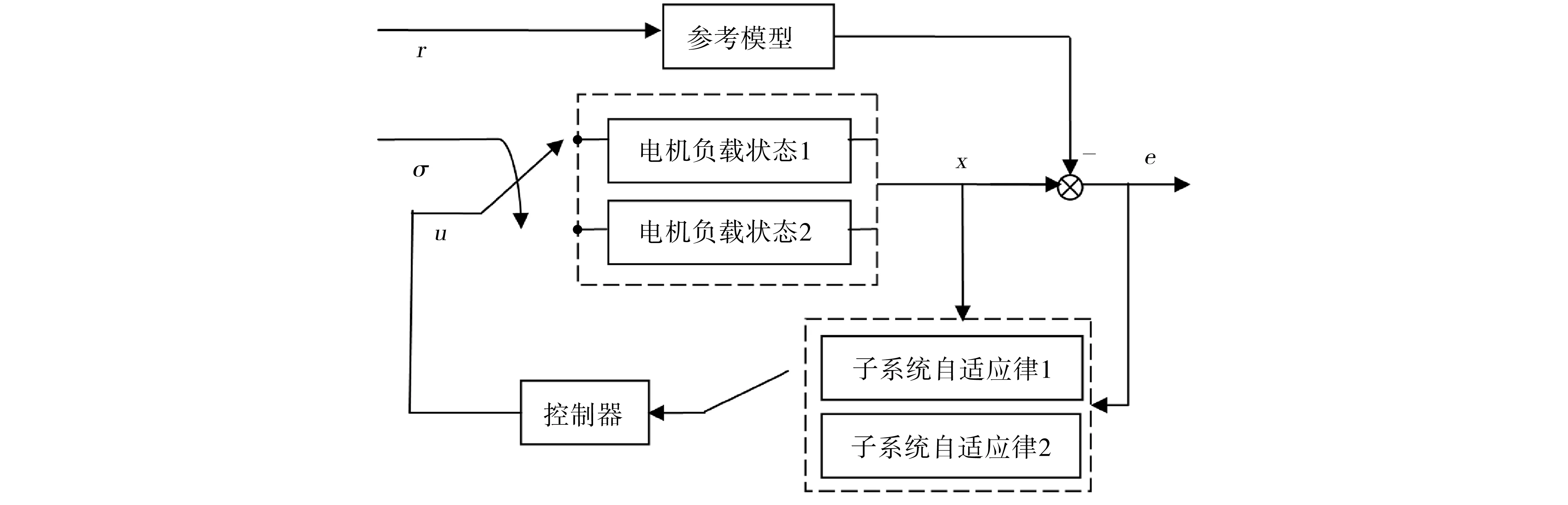
图1　状态变量和输入构成的控制器Fig.1　Controller with the state variables and input

定义跟踪误差e=xM-x，由式(6)—式(8)得到跟踪误差方程为

(10)

若参数Ai和θi已知，设计控制器

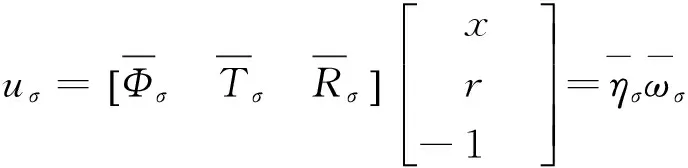
(11)

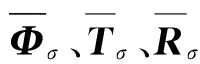
使得(AM-θσ)x+BMr-Bσu-d(t)=0，误差方程(10)变为

(12)

(13)

由于控制器与子系统同步切换，状态误差仅反映其自身估计向量的自适应控制器的控制效果，故采用分段自适应律

(14)

证明:根据自适应控制器(13)以及误差方程(10)，可得

(15)

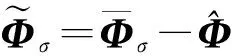
选取Lyapunov函数

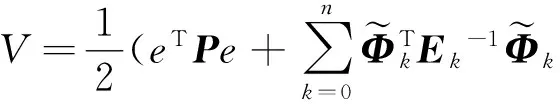
(16)

将V沿着误差系统(10)对时间求导，并利用适应律(14)得到

(17)

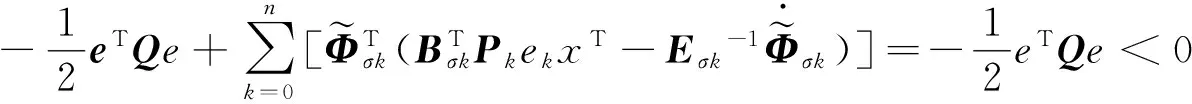
证毕.

注：切换信号会影响切换自适应控制器的动态性能,只有在对应子系统激活的时间段内，子控制器中的参数才能进行调节.若某个子系统在其他控制器参数都基本调好之后才首次激活，其参数误差会导致系统的跟踪误差增大，退出激活之后，已经增大的系统跟踪误差又会使其他子控制器中已经调好的参数偏离理想值.

3　仿真算例

本节给出10 N负载与空载状态反复切换情况下电机的自适应控制仿真，给出了不同切换信号下的仿真结果.

考虑系统实际参数，切换系统的2个子系统分别为

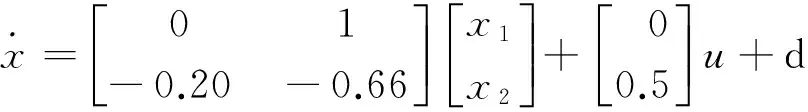
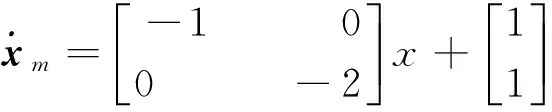
当切换信号σ=1时,为10 N负载的状态；σ=2时,为空载状态.

系统的初始条件为

xm0=[00],x0=[10],

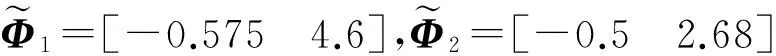
容易验证，满足定理1的条件为

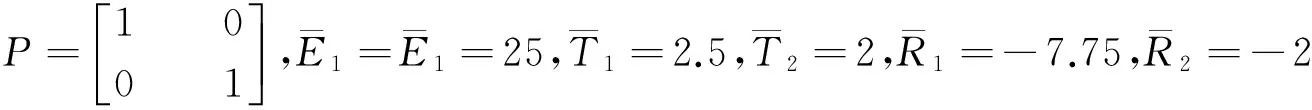
首先，选择占空比为50%的切换信号，仿真结果如图2-4所示.可见，状态跟踪误差渐近收敛于零，系统的信号、状态和控制量都是有界的.从图4可注意到，在负载跳变的时刻，控制力矩也是跳变的，正是这个突变的控制抵消了负载突变带来的影响，保证了渐近跟踪的性能.

将占空比改为70%，结果如图2-4所示.图3可见，由于占空比的改变，跟踪误差的收敛时间也变长，波动较为明显，说明切换信号会影响切换自适应控制器的动态性能.这是因为子系统参数的调节时间相对变短了，其估计参数难以收敛到理想值，从而导致整个系统调节时间的增长.

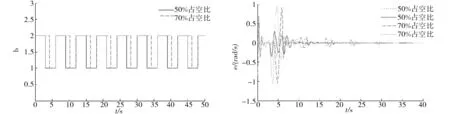
图2　切换信号 图3　状态跟踪误差 Fig.2　Switching signal Fig.3　State tracking error of the switched systems

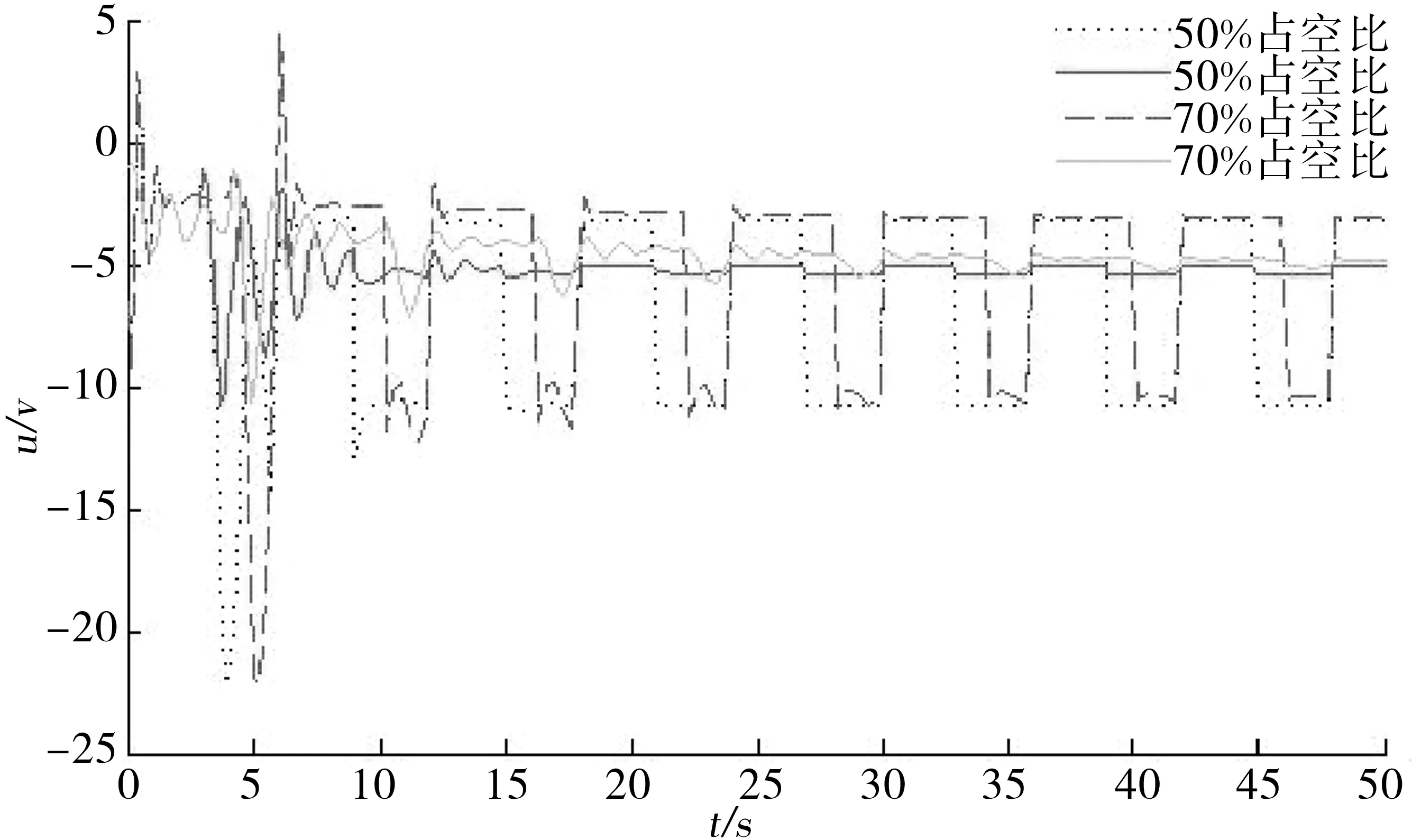
图4　切换控制器的输出Fig.4　Output of the switched controller

4　结论

针对电机负载的切换带来的系统参数跳变问题，用子系统表示不同负载下的系统参数，建立了切换电机模型.利用切换系统的模型参考自适应设计思想，为负载连续切换的电机系统设计了切换自适应跟踪控制器，有效避免了参数跳变的影响，保证了渐近跟踪性能.仿真结果验证了所设计控制器和适应律的有效性，对跳变扰动的处理也表现出很好的稳定性.

[1]纪志成,沈艳霞,薛花.无刷直流电机自适应模糊控制的研究[J].中国电机工程学报,2005,25(5):106-111.DOI:10.3321/j.issn:0258-8013.2005.05.019.

JI Zhicheng,SHEN Yanxia,XUE Hua.Study on the adaptive fuzzy control for brushless DC motor[J].Proceedings of the CSEE，2005,25(5):106-111.DOI:10.3321/j.issn:0258-8013.2005.05.019.

[2]SRDJAN M，LUKIC.State-switching control technique for switched reluctance motor drives theory[J].IEEE Transactions on Industrial Electronics,2010,57(9):2932-2938.DOI:10.1109/iemdc.2007.383622.

[3]JONATHAN FIENE G.NIEMEYER.Toward switching motor control[J].IEEE/Asme Transactions on Mechatronics,2006,111:27-34.DOI:10.1109/tmech.2005.863368.

[4]WANG D,WANG W,SHI P.ExponentialH∞filtering for switched linear systems with interval time-varying delay[J].International Journal of Robust and Nonlinear Control,2009,19(5):532-551.DOI:10.1002/rnc.1334.

[5]夏长亮,郭培健,史婷娜,等.基于模糊遗传算法的无刷直流电机自适应控制[J].中国电机工程学报,2005,25(11):129-133.DOI:10.3321/j.issn:0258-8013.2005.11.024.

XIA Changliang,GUO Peijian,SHI Tingna,et al.Control of brushless DC motor using genetic algorithm based fuzzy controller[J].Proceedings of the CSEE,2005,25(11):129-133.DOI:10.3321/j.issn:0258-8013.2005.11.024.

[6]LIN H,ANTSAKLIS P J.Stability and stabilizability of switched linear systems:a survey of recent results[J].IEEE Trans Autom Control,2009,54:308-322.DOI:10.1109/tac.2008.2012009.

[7]方志明,向峥嵘,陈庆伟.一类切换系统的输入—状态稳定性分析与优化控制[J].信息与控制,2011,40(2):155-162.DOI:10.3724/SP.J.1219.2010.00155.

FANG Zhiming,XIANG Zhengrong,CHEN Qingwei.Input-to-state stability analysis and optimal control for a class of switched systems[J].Information and Control,2011,40(2):155-162.DOI:10.3724/SP.J.1219.2010.00155.

[8]赵洪山,米增强,牛东晓,等.利用混杂系统理论进行电力系统建模的研究[J].中国电机工程学报,2003,23(1):21-26.DOI:10.3321/j.issn:0258-8013.2003.01.005.

ZHAO Hongshan,MI Zengqiang,NIU Dongxiao,et al.Power system modelling using hybrid system theory[J].Proceedings of the CSEE,2003,23(1):21-26.DOI:10.3321/j.issn:0258-8013.2003.01.005.

[9]于秀敏,曹珊,孙平,等.混合动力汽车控制策略的研究现状及其发展趋势[J].机械工程学报,2006,42(11):10-16.DOI:10.3321/j.issn:0577-6686.2006.11.002.

YU Xiumin,CAO Shan,SUN Ping,et al.Present study situation and developing trend of control strategies for hybrid electric vehicle[J].Chinese Journal of Mechanical Engineering,2006,42(11):10-16.DOI:10.3321/j.issn:0577-6686.2006.11.002.

[10]YE X M,WANG X,ZHAO J.Switched adaptive control with average dwell time for a class of robot manipulators[C].2014 33rd Chinese Control Conference (CCC),2014:8501-8506.DOI:10.1109/chicc.2014.6896427.

[11]王昕,岳恒,柴天佑.基于多模型切换的多变量直接自适应控制器[J].东北大学学报(自然科学版),2002,23(1):1-4.DOI:10.3321/j.issn:1005-3026.2002.01.001.

WANG Xin,YUN Heng,CHAI Tianyou.Multivariable direct adaptive controller using multiple models[J].Journal of Northeastern University (Natural Science),2002,23(1):1-4.DOI:10.3321/j.issn:1005-3026.2002.01.001.

[12]NIU Ben,ZHAO Xudong,ZHANG Lixian,et al.p-Times differentiable unbounded functions for robust control of uncertain switched nonlinear systems with tracking constraints[J].International Journal of Robust and Nonlinear Control,2014,1002(10):3243.DOI:10.1002/rnc.3243.

[13]SUN L Y,ZHAO J,GEORGI M D.Adaptive coordinated passivation control for generator excitation and thyristor controlled series compensation system [J].Control Engineering Practice,2009,17(7):766-772.DOI:10.1016/j.conengprac.2008.12.004.

[14]陈复扬,姜斌.自适应控制与应用[M].北京:国防工业出版社,2009.

[15]MA R C,LIU Y,ZHAO S Z,et al.Global stabilization design for switched power integrator triangular systems with different powers[J].Nonlinear Analysis:Hybrid Systems,2015,15:74-85.DOI:10.1016/j.nahs.2014.08.003.

[16]SANG Q,TAO G.Adaptive control of piecewise linear systems with state feedback for output tracking[J].Asian Journal of Control,2013,15(4):933-943.DOI:10.1002/asjc.596.

[17]WANG Q,HOU Y Z,DONG C Y.Model reference robust adaptive control for a class of uncertain switched linear systems[J].International Journal of Robust and Nonlinear Control,2010,22(9):1019-1035.DOI:10.1002/rnc.1744.

[18]BERNARDO D M,MONTANARO U,OLM J M,et al.Model reference adaptive control of discrete-time piecewise linear systems[J].International Journal of Robust and Nonlinear Control,2013,23(7):709-730.DOI:10.1002/rnc.2786.

[19]LONG L J,ZHAO J.H∞Control of switched nonlinear systems in-normal form using multiple lyapunov functions[J].IEEE Transactions on Automatic Control,2012,57(5):1285-1291.DOI:10.1109/tac.2012.2191835.

[20]MA R C,ZHAO J.Backstepping design for global stabilization of switched nonlinear systems in lower triangular form under arbitrary switchings[J].Automatica,2010,46:1819-1823.DOI:10.1016/j.automatica.2010.06.050.

[21]孙希明,付俊,孙洪飞,等.一类切换线性中立时滞系统稳定性的分析[J].中国电机工程学报,2005,23:42-46.DOI:10.3321/j.issn:0258-8013.2005.23.008.

SUN Ximing,FU Jun,SUN Hongfei,et al.Stability of linear switched neutral delay systems[J].Proceedings of the CSEE,2005,23:42-46.DOI:10.3321/j.issn:0258-8013.2005.23.008.

[22]WANG X,ZHAO J,TANG Y J.State tracking model reference adaptive control for switched nonlinear systems with linear uncertain parameters[J].Control Theory Appl,2012,10 (3):123-127.DOI:10.1007/s11768-012-1018-6.

[23]刘慧博,李朝阳.无刷直流电动机积分反演模糊滑模控制[J].工矿自动化,2014,40(3):64-69.DOI:10.13272/j.issn.1671-251x.2014.03.018.

LIU Huibo,LI Zhaoyang.Integral inversion fuzzy sliding mode control of brushless DC motor[J].Industry and Mine Automation,2014,40(3):64-69.DOI:10.13272/j.issn.1671-251x.2014.03.018.

[24]夏长亮．无刷直流电机控制系统[M]．北京：科学出版社，2009.

[25]安树．反演滑模控制在BLDCM伺服系统中的应用[J]．机械工程与自动化，2008(6)：161-163.DOI:10.3969/j.issn.1672-6413.2008.06.061.

AN Shu.Application of sliding mode control with backstepping in BLDCM servo system[J].Mechanical Engineering & Automation,2008(6)：161-163.DOI:10.3969/j.issn.1672-6413.2008.06.061.

(责任编辑：王兰英)

Adaptive control based on switched model of electric machine with transition load

ZONG Xiaoping,CUI Enchang,WANG Xia,WANG Peiguang

(Electronic Information Engineering College,Hebei University,Baoding 071002,China)

An adaptive tracking controller is designd for motor with shifting load in this paper.First,amathematic model of motor switching system is built where shifting load is regarded as a switching signal.Then adaptive controller of switching system is designed,which solves the problem of tracking error that increases rapidly after load switching and ensures asymptotic tracking of the system.Finally,examples and computer simulation validate the performance of designed controller,and the impact of switching signal on system dynamic property is explained.

transition load;switched system;adaptive control;asymptotic tracking

10.3969/j.issn.1000-1565.2016.02.015

2015-04-23

国家自然科学基金资助项目(11271106)；国家自然科学基金青年基金资助项目(61403118)；河北省高等学校科学技术研究项目(QN20131056)；河北省自然科学基金资助项目(F2015201088)

宗晓萍(1964—)，女，河北蔚县人，河北大学教授，博士，主要从事混合动态系统及智能控制方向研究.

E-mail：769085906@qq.com

TP273

A

1000-1565(2016)02-0197-07