求解扩散方程的高精度显式紧致差分格式
2016-11-07杨晓佳王燕
杨晓佳,王燕
(宁夏大学 数学计算机学院,宁夏 银川 750021)
求解扩散方程的高精度显式紧致差分格式
杨晓佳,王燕
(宁夏大学 数学计算机学院,宁夏 银川750021)
首先针对一维扩散方程,空间方向采用二阶导数的四阶紧致差分公式进行离散,时间方向采用泰勒级数展开的方法进行离散,推导出了一种高精度显式紧致差分格式;然后通过Fourier分析方法给出了格式的稳定性条件为λ≤1/2(λ为网格比);最后通过数值实验验证了格式的精确性和可靠性.
扩散方程;高精度;紧致格式;显格式;有限差分法
MSC 2010:35K20
扩散方程是一类描述物理量随时间的扩散和衰减规律的抛物型偏微分方程.自然环境、工程设备及生物机体中的许多物理现象,诸如气体的扩散、液体的渗透等都可用扩散方程来描述.由于物理问题本身的复杂性,其精确解往往不容易求得,因此研究其数值求解方法无疑具有非常重要的理论意义和实际应用价值.求解扩散方程的数值方法一般可分为显式方法和隐式方法2种.
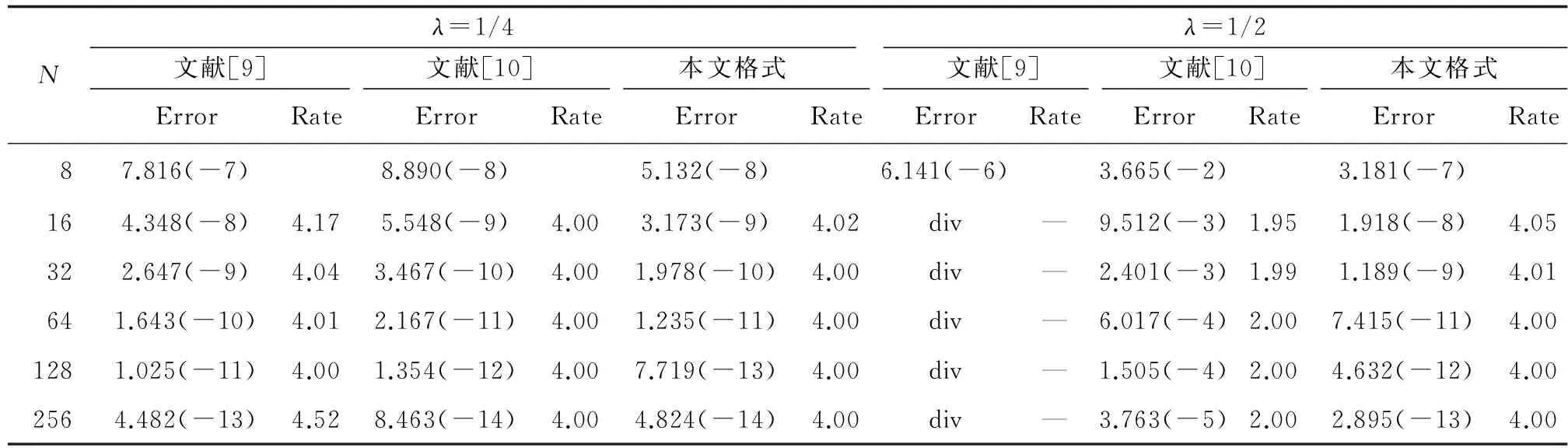
近几年来,研究者们构造了许多高精度隐式方法.文献[1]基于Hermite插值多项式的构造思路,推导出了一维含源项扩散方程的高精度隐式紧致差分格式;文献[2]利用一阶微商和二阶微商的四阶紧致差分逼近公式,推导出了求解一维扩散方程的2种精度分别为O(τ2+h4)和O(τ4+h4)隐式差分格式,其中O(τ2+h4)格式是2层无条件稳定的,而O(τ4+h4)格式是3层无条件不稳定的格式.文献[3]利用抛物型方程解的一阶偏导数在特殊节点处的一个差分近似式和二阶中心差商近似式用待定系数法构造了一族隐式差分格式,格式的截断误差为O(τ3+h4),稳定性条件为r>1/6.文献[4]用待定系数法构造了求解抛物型方程的一个高精度隐式格式,格式的截断误差达到O(τ4+h4),证明了当r>1/12时,差分格式是稳定的.文献[5]针对一维抛物型方程的初边值问题,采用待定系数法和泰勒级数展开的方法构造了一个2层8点隐式差分格式,其格式的截断误差为O(τ3+h5),稳定性条件是0.001 (1) 初始条件为 (2) 边界条件为 (3) 其中u(x,t)是待求未知函数,f(x,t)为非齐次项,a(t)、b(t)、φ(x)均为已知函数. 考虑方程(1)在第n时刻的值,对空间内部节点采用四阶精度的导数型紧致差分公式[15],则有 (4) 对于空间边界节点的处理,由式(1)与式(3)可得 (5) (6) (7) (8) 由于 (9) 因此 (10) (11) (12) 下面采用Fourier分析方法对上述建立的差分格式的稳定性进行分析.假设边界条件精确成立,且格式的源项f无误差存在. (13) (14) 对式(13)和式(14)化简整理得 (15) (16) 将式(15)代入式(16)得 (17) 从而可得式(12)的增长因子为 (18) 要使式(12)稳定,则需|G(τ,ω)|≤1,即 (19) (20) 式(20)的解为λ∈R. 为了验证本文格式的有效性和可靠性,现考虑如下4个具有精确解的初边值问题,其中边界条件给定为Dirichlet边界条件.采用Fortran 77语言进行编程,在Pentium 4个人计算机上采用双精度制进行计算.分别采用文献[2]、文献[9]、文献[10]和本文格式算法进行了计算,给出了不同时刻、不同时间步长、不同空间步长以及不同网格比λ下的最大绝对误差、CPU时间和收敛阶,其中最大绝对误差及收敛阶定义如下: 其中,Error1和Error2分别为空间网格步长为h1和h2时的最大绝对误差. 算例1[9-10] 问题1是齐次的扩散问题,其中右边界条件是关于时间t的函数,从表1计算结果可以看出,本文格式对边界的处理方法是有效的.表1给出了当t=1时,分别取网格比λ=1/4和λ=1/2,采用文献[9]、文献[10]的方法和本文格式的计算结果.文献[9]中的格式含参数η,从文中的稳定性理论分析可以看出,其格式的稳定性条件与参数有关,在接下来的计算中,均取η=-4.当网格比λ=1/4时,文献[9]、文献[10]的方法和本文格式都具有四阶精度,但本文格式的最大绝对误差小于文献[9]和文献[10]中的最大绝对误差;当网格比λ=1/2时,从表中可以看出,当网格数N=16时,文献[9]的计算结果就发散了;采用文献[10]所得的最大绝对误差要比本文格式大3~6个数量级,而且文献[10]的方法只具有二阶精度,但本文格式仍具有四阶精度.表2给出了网格比λ=3/8和λ=1/2时,N=10,n=200(n=t/τ为总的时间步数)时问题1的数值解和精确解,从表中可以看出本文格式的计算结果较文献[9]和文献[10]的计算结果更精确.同时可以看出,文献[9]中的结果发散.‘div’表示结果发散,下同. 表1 问题1在t=1时刻的最大绝对误差及收敛阶 表2 问题1在N=10的数值解和精确解 算例2 表3给出了问题2在t=1时,分别取网格比λ=1/4和λ=1/2,采用文献[9]、文献[10]的方法和本文格式的最大绝对误差及收敛阶,从表中的计算结果可以看出,当网格比λ=1/4,文献[9]、文献[10]的方法和本文格式都具有四阶精度,但本文格式的最大绝对误差小于文献[9]和文献[10];当网格比λ=1/2时,当网格数N=16时,文献[9]的计算结果发散;本文格式的最大绝对误差要比文献[10]小5~8个数量级,而且文献[10]的方法只具有二阶精度,但本文格式仍具有四阶精度;表4给出了网格比λ=3/8和λ=1/2时,N=10,n=200(其中n=t/τ为总的时间步数)时的问题2的数值解和精确解,从表中可以看出本文格式的计算结果较文献[9]和文献[10]的计算结果更加精确,这有效地验证了本文格式的精确性和可靠性.当λ=1/2时,从表4中的计算结果可以看出,文献[9]的计算结果是收敛的,这说明文献[9]的方法对所求解的问题有依赖性,取同样的参数,计算问题2时结果收敛,而计算问题1时结果却发散. 表3 问题2在t=1时刻的最大绝对误差及收敛阶 表4 问题2在N=10的数值解和精确解 问题3是非齐次的扩散方程,由于文献[9]和文献[10]中未给出关于非齐次问题的求解格式,因此,无法与文献[9]和文献[10]作比较.对于这个问题,与文献[2]的高精度隐格式进行了比较.问题3的边界条件是关于时间t的函数,从表5中的计算结果可知,本文格式对此类问题是有效的,特别是对边界的处理方法是可靠的;表5给出了问题3在λ=1/3和λ=1/2时的最大绝对误差、CPU时间T及收敛阶,由最大计算误差可知,本文格式比文献[2]更精确,从CPU时间T来看,本文格式计算所需的CPU时间T比文献[2]的CPU时间少,特别是当λ=1/2时,取时间t=5,网格数为N=256时,文献[2]所用CPU时间T为117.0,而本文格式仅为63.15,这说明本文显格式在计算网格数比较大且时间歩循环比较多的问题时具有一定的优势,在网格充分细化的计算过程中,能有效地节省存储空间和降低计算成本. 表5 问题3在t=1时刻的最大绝对误差、CPU时间及收敛阶Rate 本文对一维扩散方程初边值问题的显式高精度紧致差分格式进行了研究,得出以下结论: 1)采用四阶紧致差分公式对空间二阶导数进行离散,采用泰勒级数展开的方法对时间导数项进行离散,推导得到了一种数值求解一维扩散方程的显式高精度紧致差分格式,截断误差为O(τ2+τh2+h4),并通过Fourier方法分析了格式的稳定性,其稳定性条件为λ≤1/2.通过数值实验,验证了其精确性和稳定性. 2)目前已经发展的求解扩散问题的高精度格式多为3层格式,如文献[9-10,12-13],对3层格式的计算,需要采用另外的格式进行启动,即完成第1个时间步的计算.而本文格式为2层格式,直接由初值步开始依次计算,并且本文格式与文献[9-10]中的格式具有相同的稳定性条件,但是本文格式的计算结果却更为精确. 3)将本文格式与同阶精度的隐式方法[2]进行了比较,尽管本文方法的稳定性不及隐式方法,但是在本文方法的稳定性条件满足的情况下,取相同的计算参数,本文方法可以得到较隐式方法[2]更为精确的计算结果,并且由于本文方法是显式计算,因此较隐式方法的计算量大为减少,提高了问题的求解效率,节约了CPU时间. [1]田振夫.一维对流扩散方程的四阶精度有限差分法[J].宁夏大学学报(自然科学版),1995,16(1):30-35. TIAN Zhenfu.Fourth-order finite difference methods for one-dimensional convection-diffusion equations[J].Journal of Ningxia University(Natural Science Edition),1995,16(1):30-35. [2]葛永斌,田振夫,詹咏,等.求解扩散方程的一种高精度隐式差分方法[J].上海理工大学学报,2005,27(2):107-112.DOI:10.3969/j.issn.1007-6735.2005.02.004. GE Yongbin,TIAN Zhenfu,ZHAN Yong,et al.High order implicit difference method for the diffusion equation[J].Journal of University of Shanghai for Science and Technology,2005,27(2):107-112.DOI:10.3969/j.issn.1007-6735.2005.02.004. [3]詹涌强,张传林.解抛物型方程的一族高精度隐式差分格式[J].应用数学和力学,2014,35(7):790-797.DOI:10.3879/j.issn.1000-0887.2014.07.008. ZHAN Yongqiang,ZHANG Chuanlin.A family of high accuracy implicit difference schemes for solving parabolic equatons[J].Applied Mathematics and Mechanics,2014,35(7):790-797.DOI:10.3879/j.issn.1000-0887.2014.07.008. [4]詹涌强,张传林.解抛物型方程的一个新的高精度隐格式[J].华中师范大学学报(自然科学版),2014,48(2):168-170. ZHAN Yongqiang,ZHANG Chuanlin.A new high accuracy implicit difference schemes for solving parabolic equatons[J].Journal of Huazhong Normal University(Natural Science Edition),2014,48(2):168-170. [5]周敏,高学军,董超.解抛物型方程的八点隐式差分格式[J].广东工业大学学报,2014,31(4):71-78.DOI:10.3969/j.issn.1007-7162.2014.04.013. ZHOU Min,GAO Xuejun,DONG Chao.The implicitght difference scheme of eight points for solving the parabolic equtions[J].Journal of Guangdong University of Technology,2014,31(4):71-78.DOI:10.3969/j.issn.1007-7162.2014.04.013. [6]于德浩,汤华中.偏微分方程数值解法[M].北京:科学出版社,2004:106-109. YU Dehao,TANG Huazhong.Numerical solution of partial differential equation[M].Beijing:Science Press,2004:106-109. [7]杨情民.解抛物型方程的一族显格式[J].高等学校计算数学学报.1981,4:306-317. YANG Qingmin.A family of explicit schemes for solving the parabolic equations[J].Journal of High School Mathematics,1981,4:306-317. [8]曾文平.多维抛物型方程的分支绝对稳定的显式格式[J].高等学校计算数学学报,1997,19(2):112-121. ZENG Wenping.Explicit scheme for the absolute stability of the multi dimensional parabolic equations[J].Journal of High School Mathematics,1997,19(2):112-121. [9]金承日.解抛物型方程的高精度显式差分格式[J].计算数学,1991,13(1):38-44.DOI:10.3321/j.issn:0254-7791.1991.01.001. JIN Chengri.High accuracy explicit difference scheme for solving parabolic equations[J].Computational Mathematics,1991,13(1):38-44.DOI:10.3321/j.issn:0254-7791.1991.01.001. [10]马明书.一维抛物型方程的一个新的高精度显式差分格式[J].数值计算与计算机应用,2001,22(2):156-160.DOI:10.3969/j.issn.1000-3266.2001.02.010. MA Mingshu.A new high accuracy explicit difference scheme with branching stable for solving parabolic equation of one-dimension[J].Numerical Computation and Computer Application,2001,22(2):156-160.DOI:10.3969/j.issn.1000-3266.2001.02.010. [11]马明书.抛物型方程的一个新的显格式[J].纺织高校基础科学学报,2001,14(2):133-135.DOI:10.3969/j.issn.1006-8341.2001.02.010. MA Mingshu.A new explicit difference scheme with high accuracy for solving parabolic type equation[J].Journal of Basic Science of Textile University,2001,14(2):133-135.DOI:10.3969/j.issn.1006-8341.2001.02.010. [12]徐金平,单双荣.解抛物型方程的一个高精度显式差分格式[J].华侨大学学报(自然科学版),2009,30(4):473-475.DOI:10.11830/ISSN.1000-5013.2009.04.0473. XU Jinping,SHAN Shuangrong.An explicit difference scheme with high-order accuracy for solving parabolic equation[J].Journal of Huaqiao University(Natural Science),2009,30(4):473-475.DOI:10.11830/ISSN.1000-5013.2009.04.0473. [13]袁权龙,詹再东.抛物方程高精度高稳定显格式研究[J].山西师范大学学报(自然科学版),2009,23(4):27-30.DOI:10.3969/j.issn.1009-4490.2009.04.007. YUAN Quanlong,ZHAN Zaidong.High accuracy and stable explicit scheme for the parabolic equation[J].Journal of Shanxi Normal University(Natural Science Edition),2009,23(4):27-30.DOI:10.3969/j.issn.1009-4490.2009.04.007. [14]WEN ruihao,Shao Hongzhu.Domain decomposition schemes with high-order accuracy and unconditional stability[J].Appl Math Comput,2013,219:6170-6181.DOI:http://dx.doi.org/10.1016/j.amc.2012.12.001. [15]LELE S K.Compact finite difference schemes with spectral-like resolution[J].J Comput Phys,1992,103:16-42. (责任编辑:王兰英) High accuracy explicit compact difference scheme for the diffusion equation YANG Xiaojia,WANG Yan (College of Mathematics and Computer Science,Ningxia University,Yinchuan 750021,China) Based on the fourth-order compact difference formula of the second-order derivative in spatial direction and Taylor series expansion in time direction,a high-order explicit compact difference scheme for the one dimentional diffusion equation is developed.The stability of the scheme is analyzed by Fourier method,and the condition of stability isλ≤1/2 (λis the mesh ratio).Numerical experiments are carried out to verify the accuracy and reliability of the present scheme. diffusion equation;high accuracy;compact scheme;explicit scheme;finite difference method 10.3969/j.issn.1000-1565.2016.02.002 2015-09-08 宁夏高等学校科学技术研究项目(NGY2013019) 杨晓佳(1988—),女,宁夏吴忠人,宁夏大学在读硕士研究生.E-mail:yang_xiaoj@sina.com 王燕(1976—),女,宁夏银川人,宁夏大学副教授,主要从事偏微分方程数值解法的研究. E-mail:wangy@nxu.edu.cn O241.82 A 1000-1565(2016)02-0117-07
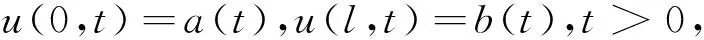
1 差分格式的建立





2 稳定性分析

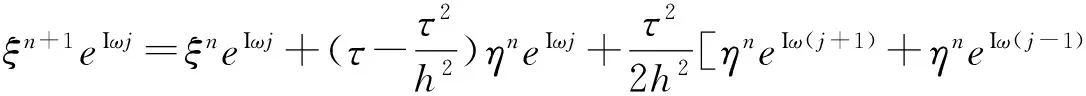
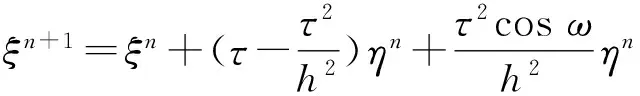
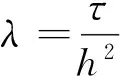
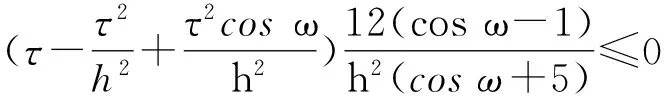
3 数值实验
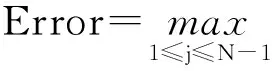





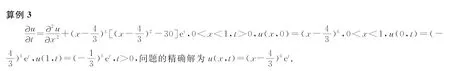

4 结论
