基于Hybrid样本的学习过程一致收敛速度的界

李俊华，白鹤举

(1.河北大学 数学与信息科学学院，河北 保定　071002；2.承德石油高等专科学校 基础教学部，河北 承德　067000)



基于Hybrid样本的学习过程一致收敛速度的界

李俊华，白鹤举

(1.河北大学 数学与信息科学学院，河北 保定071002；2.承德石油高等专科学校 基础教学部，河北 承德067000)

学习过程收敛速度的界是统计学习理论的重要组成部分,这些界决定了学习机器的推广能力.以机会理论和Hybrid变量的概念为基础,讨论了基于Hybrid样本的学习过程一致收敛速度的界,并给出了这些界和函数容量之间的关系.

Hybrid变量;Hybrid经验风险最小化原则;一致收敛速度的界

MSC 2010:28E10

统计学习理论(statistical learning theory,简称SLT)是专门针对小样本情况研究机器学习规律的理论,学习理论的关键定理和学习过程收敛速度的界在SLT中起着非常重要的作用,学习理论的关键定理给出了基于经验风险最小化原则的学习过程一致性的充分必要条件,而通过对学习过程收敛速度的界的讨论则可以进一步研究基于经验风险最小化原则的学习机器的推广能力.文献[1]给出了基于Hybrid样本的学习理论的关键定理,本文将在此基础上,进一步讨论基于Hybrid样本的学习过程一致收敛速度的界.

1　预备知识

定义1[2]设(Θ,P,Cr)是可信性空间,(Ω,A,Pr)是概率空间,则(Θ,P,Cr)×(Ω,A,Pr)称为机会空间.

性质1[2]设(Θ,P,Cr)×(Ω,A,Pr)是机会空间,则机会测度Ch满足以下性质:

1)Ch{Ø}=0,Ch{Θ×Ω}=1;2)对任意事件Λ,有0≤Ch{Λ}≤1;3)若事件Λ1⊆Λ2,则Ch{Λ1}≤Ch{Λ2};4)对任意事件Λ,有Ch{Λ}+Ch{Λc}=1;5)对任意事件Λ1和Λ2,有Ch{Λ1∪Λ2}≤Ch{Λ1}+Ch{Λ2}.

定义2[2]设ξ是一个从机会空间(Θ,P,Cr)×(Ω,A,Pr)到实数集R的可测函数,若对任意R上的Borel 集B,都有{ξ∈B}={(θ,ω)∈Θ×Ω|ξ(θ,ω)∈B}是一个事件,称ξ是一个Hybrid变量.

定义3[2]若对任意R上Borel集B,Hybrid变量ξ和η满足Ch{ξ∈B}=Ch{η∈B},称ξ和η是同分布的.

定义5[2]设Hybrid变量ξ1和ξ2的机会密度函数分别是f1(x)和f2(x),f(x,y)是(ξ1,ξ2)的联合密度函数.若对任意x,y∈R,都有f(x,y)=f1(x)f2(y),称ξ1和ξ2是相互独立的.

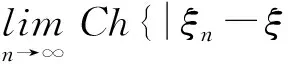
证明由ξ的非负性及机会测度的单调性,则

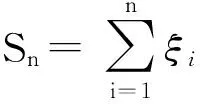
证明对任意实数λ>0,由引理1,得

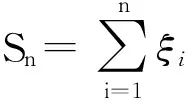
证明由引理2和引理3得

2　主要结果

统计学习理论中关于经验风险和实际风险之间的关系的重要结论被称为推广性的界,它是分析学习机器性能和发展新的学习算法的重要基础[3-5].学习过程一致收敛速度的界是推广性的界的重要组成部分,通过对这些界的讨论可以得到在经验风险最小化原则中经验风险与实际风险的关系,进而可以研究学习机器的推广能力[3-7].

设z1,z2,…，zl是独立同分布的Hybrid样本,Q(z,α),α∈Λ是可测损失函数集合.

定义7[1]机会空间上基于Hybrid样本的期望风险泛函和经验风险泛函分别定义为

定义8[1]把Hybrid期望风险泛函替换为Hybrid经验风险泛函,并用使Hybrid经验风险泛函最小的函数Q(z,αl)逼近使Hybrid期望风险泛函最小的函数Q(z,α0),这一原则称作Hybrid经验风险最小化原则(Hybridempiricalriskminimizationprinciple,简称HERM原则).

要估计经验风险最小化的推广能力,需要回答以下2个问题:

1)取到最小经验风险的函数Q(z,αl)所取得的真实风险Rch(αl)是什么？

假设函数集合包含有限的N个元素Q(z,αk),k=1,2,…，N,且A≤Q(z,αk)≤B.

定理3对于函数集Q(z,αk),k=1,2,…,N的所有N个函数,不等式

(1)

依至少1-η的机会测度成立.

证明利用引理4,有

由定理3,特别地,对于函数Q(z,αl),不等式

(2)

依至少1-η的机会测度成立.式(2)通过估计Rch(αl)的值,给出了函数Q(z,αl)所提供的真实风险Rch(αl)的上界,从而回答了第1个问题.

定理4对于函数集合Q(z,αk),k=1,2,…，N的所有N个函数,不等式

依至少1-2η的机会测度成立.

证明对于最小化Hybrid期望风险泛函的函数Q(z,α0),因为

(3)

依至少1-2η的机会测度成立.

3　结论

在基于Hybrid样本的学习理论关键定理的基础上,讨论了基于Hybrid样本的学习过程一致收敛速度的界,给出了所选函数风险的上界以及这一上界与函数集的最小可能风险值之间的接近程度和误差,为进一步建立基于Hybrid样本的统计学习理论并构建相应的支持向量机奠定了理论基础.

[1]SUN Xiaojing,WANG Chao,HA Minghu,et al.The key theorem of learning theory based on hybrid variable[C]//Guilin:Proceedings of the International Conference on Machine Learning and Cybenetics,2011:1141-1145.

[2]LIUBaoding.Uncertaintytheory[DB/OL].(2010)[2015-09-20].http://www.doc88.com/p-34688422/032.html.

[3]VAPNIKVN.Statisticallearningtheory[M].NewYork:AWiley-IntersciencePublication,1998.

[4]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-44.

ZHANGXuegong.Introductiontostatisticallearningtheoryandsupportvectormachines[J].ActaAutomaticaSinica,2000,26(1):32-44.

[5]哈明虎,王超,张植明,等.不确定统计学习理论[M].北京:科学出版社,2010.

[6]哈明虎,王鹏.可能性空间中学习过程一致收敛速度的界[J].河北大学学报(自然科学版),2004,24(1):1-6.

HAMinghu,WANGPeng.Boundsontherateofuniformconvergenceoflearningprocessonpossibilityspaces[J].JournalofHebeiUniversity(NaturalScienceEdition),2004,24(1):1-6.

[7]田景峰,张植明.可信性空间上基于复模糊变量的学习过程一致收敛速度的界[J].华北电力大学学报,2009,36(5):106-112.

TIANJingfeng,ZHANGZhiming.Theboundsontherateofuniformconvergenceoflearningprocessbasedoncomplexfuzzyvariableoncredibilityspace[J].JournalofNorthChinaElectricPowerUniversity,2009,36(5):106-112.

(责任编辑：王兰英)

Bounds on the rate of uniform convergence of learning process based on Hybrid samples

LI Junhua1,BAI Heju2

(1.College of Mathematics and Information Science,Hebei University,Baoding 071002,China；2.Basic Teaching Department,Chengde Petroleum College,Chengde 067000,China)

Bounds on the rate of uniform convergence of learning process are important component part of statistical learning theory and the bounds determine the generalization abilities of learning machines.Based on the chance theory and the definition of Hybrid variable,bounds on the rate of uniform convergence of learning process based on hybrid samples are discussed and the relationship between the bounds and the capacity of the set of functions is given.

Hybrid variable;Hybrid empirical risk minimization principle;the rate of uniform convergence

10.3969/j.issn.1000-1565.2016.02.001

2015-07-01

国家自然科学基金资助项目(11201110);河北省教育厅资助项目(QN20131055)

李俊华 (1979—)，女，河北衡水人，河北大学讲师，主要从事不确定统计学习理论研究.E-mail：junhuali2008@126.com

TP18

A

1000-1565(2016)02-0113-04