基于萤火虫算法的多中继选择策略
2016-11-05程铜龙
程铜龙, 张 涵
(华南师范大学物理与电信工程学院,广州 510006)
基于萤火虫算法的多中继选择策略
程铜龙, 张涵*
(华南师范大学物理与电信工程学院,广州 510006)
中继选择(RS)和功率控制是无线中继网络的2个重要组成部分.当中继节点以全功率协作和不协作时,中继选择等同于功率控制.因此,最佳信噪比(SNR)被描述称为0-1非线性整数规划问题(0-1 nonlinear programming integer problem,NLIP).文中提出了基于萤火虫算法(Glowworm Swarm Optimization, GSO)的多中继选择策略,仿真结果表明,基于GSO算法的多中继选择能够获得最佳信噪比值,且性能优于穷举搜索、单一RS方案及其他次优化方案.
无线网络; 多中继选择; 萤火虫算法
随着无线通信技术的发展和通信需求的日益提高,追求更高效的通信网络结构、组网方式已经成为研究的热点问题[1-2].引入中继的协作通信能够在不降低发射功率的前提下,提高系统容量,减少多径衰落[3],适用于分散控制的异构通信网络环境.用于协作通信的中继方案主要有:放大转发(Amplify-and-Forward,AF)[3]、解码转发(Decode-and-Forward,DF)[4]和编码协作(Coded Cooperation,CC)[5],其中, AF方式操控简单,被视为协作通信的主流方法.
作为协作通信的关键问题,中继选择和功率控制受到了广泛研究.研究中继传输最优节点选择问题,得到次优结果[6-8],但是,当最优节点不能工作或选择错误时,此策略将大幅度降低系统性能.分析多中继选择问题,可得到比最优中继选择更优的系统性能[9-11]. JING和JAFARKHANI[9]针对协作通信的功率控制和中继选择提出了0或最大功率传输模式,即1个中继节点采取0或最大功率进行传输(对中继节点进行选择),得到了次优结果,但当中继节点数增加时,却无法进一步提高系统性能.
DU等[12]将萤火虫算法和粒子群算法[13]、遗传算法[14]、鱼群算法[15]进行比较,发现萤火虫算法的不同在于萤火虫种群可随机更新并根据适应度函数评价个体优劣,寻找更优个体,具有更快的收敛速度和更强的搜索能力,已被成功应用于多模态函数优化、多信号源追踪定位和机器人学习等领域[16-19].
目前将萤火虫算法应用到解决中继节点选择问题尚无文献报道.本文在文献[9]1415模型基础上,提出了一种基于萤火虫算法的AF模式多中继节点选择策略,建立0-1非线性整数规划问题(0-1 NLIP)模型,通过离散化萤火虫算法搜索选择最优中继节点,实现系统信噪比最大化.
1 研究方法
1.1系统模型
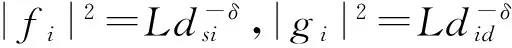

图1 系统模型
1.2问题描述
系统1次中继传输分为2步.
第一步,源节点s以功率P向中继节点i发送信号x,第i个中继接收信号为:
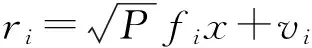
(1)
其中,vi为均值0、方差1的高斯噪声.
第二步,中继节点i对接收到的源节点信号放大处理并转发给目的节点,放大信号[9]1415为:
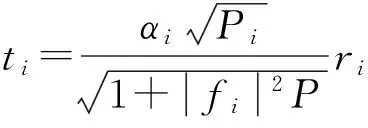
(2)
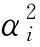
目的节点接收信号为:

(3)
其中,wi为均值0、方差1的高斯噪声.
根据式(1)~(3),得到目的节点接收信号为:
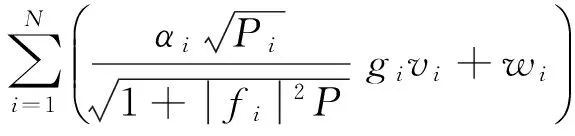
(4)
由式(4)可知,目的节点接收信号分为信号和与噪声和2部分.由于vi和wi具有相同的分布,所以式(4)可以改写为
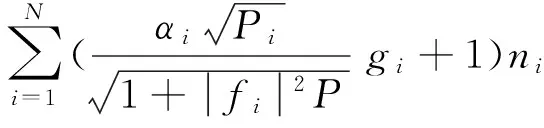
(5)
其中,ni为均值0、方差1的高斯噪声.
根据式(5)得到目的节点信噪比为:

(6)
则式(6)为
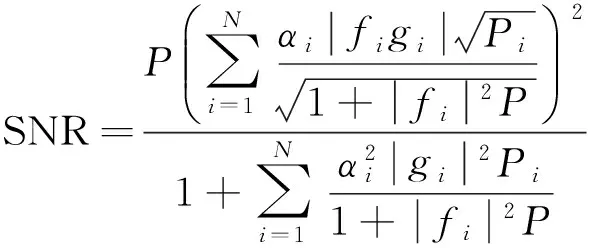
(7)
本文考虑中继节点选择问题,不考虑功率分配问题,因此得到如下优化问题:

(8)
由于优化问题式(8)中含有整数变量αi,目标函数SNR是关于变量αi的非线性函数,因此优化问题式(8)为典型的NP-hard问题中的0-1 NLIP问题[20].
1.3萤火虫算法和多中继选择
GSO算法是由KRISHNANAND和GHOSE[21]提出,最早用于求解多个连续函数最优值问题上,近年来受到多方面学者关注和应用[22-23].在该算法中,包含M个萤火虫的种群随机分配到目标函数定义域内,每只萤火虫j(j=1,2,…,M)随机分配位置lj,荧光素Bj(取决于萤火虫所在位置的目标值),视野范围rdj(称为决策半径).萤火虫j根据决策半径寻找比其荧光素更高的萤火虫m(m=1,2,…,M),并向其移动.最后,所有萤火虫都聚集在函数最优解周围,实现目标函数最优值的搜索和优化.算法开始,每只萤火虫分配相同的荧光素和决策半径,通过迭代寻找函数最优解,每次搜索过程包含2个阶段[24]:
(1)更新阶段:萤火虫j根据式(9)更新荧光素值:
Bj(t)=(1-rh)×Bj(t-1)+γ×f(lj),
(9)
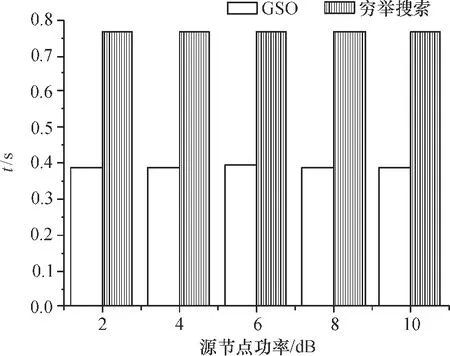
其中,Bj(t-1)为萤火虫j之前荧光素值.rh(0 (2)移动阶段:萤火虫j利用式(10)得到决策范围内比自己荧光素更高的萤火虫个体. Nmtj(t)={m:‖lm-lj‖ (10) 其中,Nmtj(t)为萤火虫j当前时刻决策范围内荧光素较高的萤火虫个体,rdj为萤火虫j视野范围(决策半径),Bm和Bj分别为萤火虫m和j的荧光素,‖lm-lj‖为萤火虫位置距离. 根据式(10)得出萤火虫j向Nmtj内萤火虫移动的概率: (11) 萤火虫j通过轮盘方法在Nmtj内选择移动概率最大的萤火虫并向其移动,移动公式为: (12) 其中,step0为移动步长. 位置更新后,萤火虫j利用式(12)更新决策半径: rdj(t)=min{rs,max[0,rdj(t-1)+ (13) Step1:初始化萤火虫相关参数值,收敛常数e=1×10-5.由于待解决问题为0-1问题,所以需要对萤火虫初始位置进行离散化操作: (14) 收敛条件为:bestfun(t)-bestfun(t-1)≤e&bestfun(t)>bestfun(t-1),其中bestfun(t)表示第t次迭代的最佳值. Step2:根据式(7)~(9)设置每只萤火虫的荧光素. Step3:根据式(10)选择萤火虫j视野范围内的萤火虫数目. Step4:根据式(11)计算萤火虫向Nmtj内每只萤火虫移动的概率,利用轮盘方法找出萤火虫j移动方向. Step5:根据式(15)更新萤火虫j的位置 (15) 由于本文解决的问题为0-1 NLIP问题,所以需要将基于连续的位置更新策略改变为适应于离散状态下的位置更新策略(具体更新方式为式(15)). Step6:根据式(13)更新萤火虫决策半径. Step7:满足最大迭代次数或收敛条件,返回最优解;否则t=t+1,返回Step2. 仿真平台为Matlab2010a,CPU为Intel(R) i3,2.1 GHz,内存2 GB,Win7操作系统.仿真假设在静态瑞利信道且L=1的无线环境下进行,中继节点数为N(N=4,5,6,7,8),所有中继节点采用(1)相同功率P1=P2=…=PN=10 dB;(2)不同功率Pmax=10 dB,路径损耗因子为4.萤火虫算法详细参数设置如表1所示,中继距离参数(为便于计算,取相对值)dsn和dnd取分布区间为[0.1,2]范围内的随机值,dsn(n=1,2,…,N)表示源节点到中继节点的距离;dnd(n=1,2,…,N)表示目的节点到中继节点的距离.表1同时列出了当N=4时的中继距离参数. 表1 GSO参数及节点距离 在上述参数设定下,对萤火虫算法(GSO)与传统的穷举搜索(Exhaustive)、单个中继选择[6]662及次优中继选择方案[9]1417进行了比较仿真.图2表明,萤火虫算法和穷举搜索得出了相同的信噪比值,同时,显示了萤火虫算法中继选择的信噪比明显优于单个最优中继选择和次优中继选择,说明萤火虫算法在解决中继节点问题上是可行的. 图2 不同策略下的最大信噪比 (N=4) 为验证所提萤火虫算法的有效性,图3给出了相同条件下萤火虫算法和穷举搜索计算所需要的运行时间,萤火虫算法耗时为0.385 s,仅为穷举搜索所需时间(0.765 s)的50%,说明萤火虫算法能够更快地获得搜索结果.图4验证了萤火虫算法与次优中继选择方案在中继节点数增加时的复杂度.当中继节点数增加时,萤火虫算法和次优化算法计算所需时间基本上与节点数N呈线性关系,但是理论上当N增大时,穷举所搜所需要的时间与2N-1有关,将呈级数增长,因此萤火虫算法在多中继节点选择问题中可以有效地缩减选择时间,提升系统性能. 图3 不同源节点功率模拟的运行时间 (N=4) 图4 不同中继节点数量模拟的运行时间(P=10 dB)Figure 4 Running time by different relay node numbers (P=10 dB) 本文将萤火虫算法应用于解决认知无线电多中继选择问题中,对萤火虫算法进行适当变化,使之适应0-1 NLIP模型,给出了目标函数和基于萤火虫算法的中继选择步骤,通过多次迭代得到多中继节点的选择方案.相较传统的穷举搜索算法、最优节点选择算法和次优节点选择算法,所提方案性能更优,获得结果更快.因此,应用萤火虫算法解决协作通信多中继选择问题具有明显的优越性. [1]FRANK H P, KATZ F. Cooperation in wireless networks: principles and applications: real egoistic behavior is to cooperate![M].New Jersey:Springer,2006:13-26. [2]SENDONARIS A, ERKIP E, AAZHANG B. User co-operation diversity. Part I. System description[J]. IEEE Transactions on Communications, 2003, 51(11): 1927-1938. [3]SENDONARIS A, ERKIP E, AAZHANG B. User co-operation diversity. Part II. Implementation aspects and performance analysis[J]. IEEE Transactions on Communications, 2003, 51(11): 1927-1948. [4]LANEMAN J N, TSE D N C, WORNELL G W. Cooperative diversity in wireless networks: efficient protocols and outage behavior[J]. IEEE Transactions on Information Theory, 2004, 50(12): 3062-3080. [5]HUNTER T E. Diversity through coded cooperation[J]. IEEE Transactions on Wireless Communications, 2006, 5(2): 283-289. [6]BLETSAS A, KHISTI A, REED D P, et al. A simple cooperative diversity method based on network path selection[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(3): 659-672. [7]IBRAHIM A S, SADEK A K, SU W, et al. SPC12-5: relay selection in multi-node cooperative communications: when to cooperate and whom to cooperate with?[C]∥Global Telecommunica-tions Conference, GLOBECOM06. San Francisco: IEEE, 2006: 1-5. [8]SOYSA M, SURAWEERA H A, TELLAMBURA C, et al. Partial and opportunistic relay selection with outdated channel estimates[J]. IEEE Transactions on Communications,2012, 60(3): 840-850. [9]JING Y, JAFARKHANI H. Single and multiple relay selection schemes and their achievable diversity orders[J]. IEEE Transactions on Wireless Communications, 2009, 8(3): 1414-1423. [10]JING Y, JAFARKHANI H. Network beamforming using relays with perfect channel information[J]. IEEE Transactions on Information Theory, 2009, 55(6): 2499-2517. [11]ATAPATTU S, JING Y, JIANG H, et al. Relay selection and performance analysis in multiple-user networks[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(8): 1517-1529. [12]DU M, LEI X, WU Z. A simplified glowworm swarm optimization algorithm[C]∥2014 IEEE Congress on Evolutionary Computation (CEC). Beijing: IEEE, 2014: 2861-2868. [13]KUO R J, YANG C Y. Simulation optimization using particle swarm optimization algorithm with application to assembly line design[J]. Applied Soft Computing, 2011, 11(1): 605-613. [14]LIANG Y, LEUNG K S. Genetic Algorithm with adaptive elitist-population strategies for multimodal function optimization[J]. Applied Soft Computing, 2011, 11(2): 2017-2034. [15]LEI X, HUANG X, ZHANG A. Improved artificial bee colony algorithm and its application in data clustering[C]∥Bio-Inspired Computing: 2010 IEEE Fifth International Conference on Theories and Applications (BIC-TA). Shanghai: IEEE,2010: 514-521. [16]KRISHNANAND K N, GHOSE D. Glowworm swarm based optimization algorithm for multimodal functions with collective robotics applications[J]. Multiagent and Grid Systems, 2006, 2(3): 209-222. [17]KRISHNANAND K N, GHOSE D. Theoretical foundations for rendezvous of glowworm-inspired agent swarms at multiple locations[J]. Robotics and Autonomous Systems, 2008, 56(7): 549-569. [18]KRISHNANAND K N, GHOSE D. Glowworm swarm optimisation: a new method for optimising multi-modal functions[J]. International Journal of Computational Intelligence Studies, 2009, 1(1): 93-119. [19]KRISHNANAND K N, GHOSE D. Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions[J]. Swarm Intelligence, 2009, 3(2): 87-124. [20]HANSEN P. Methods of nonlinear 0-1 programming[J]. Annals of Discrete Mathematics, 1979, 5(8): 53. [21]KRISHNANAND K N, GHOSE D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics[C]∥ Proceedings of the 2005 IEEE Swarm Intelligence Symposium. Piscatawag: IEEE, 2005: 86. [22]ALJARAH I, LUDWIG S A. A new clustering approach based on glowworm swarm optimization[C]∥ 2013 IEEE Congress on Evolutionary Computation (CEC). Cancun: IEEE,2013: 2642-2649. [23]HE D X,LIU G Q,ZHU H Z.Glowworm swarm optimization algorithm for solving multi-objective optimization problem[C]∥Proceedings of the 9th International Conference on Compu-tational Intelligence and Security.Le-shan: IEEE,2013:11-15. [24]唐思腾,刘紫燕,帅暘.基于萤火虫算法的多中继功率分配[J]. 电讯技术,2014, 54(10):1407-1412. TANG S T,LIU Z Y,SHUAI Y.Power allocation for multi-relay cooperative systems based on glowworm swarm optimization algorithm[J].Telecommunication Engineering,2014,54(10):1409. 【中文责编:成文英文责编:肖菁】 Multiple Relay Selection Scheme Based on Glowworm Swarm Optimization Algorithm CHENG Tonglong, ZHANG Han* (School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China) Relay selection (RS) and power control are two essential parts in wireless relay network. RS is equal to power control in the condition that a relay cooperates with its full power or without any cooperation. Thus, the optimal signal-to-noise ratio (SNR) is interpreted as a 0-1 nonlinear programming integer problem (NLIP). A Glowworm Swarm Optimization (GSO) based multiple relay selection (MRS) scheme is proposed, which can fully obtain the optimal SNR value. Simulations results show that the proposed GSO-aided MRS scheme is superior to the conventional schemes, including the exhaustive search methods, single RS scheme and other suboptimal MRS schemes. wireless network; multiple relay selection; glowworm swarm optimization 2015-04-27《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(61471176,61002012);广东省自然科学基金项目(S2013010016297);广东省数字信号与图像处理技术重点实验室开放基金项目(2015);广东省高等学校优秀青年教师培养计划项目(YQ2015046) 张涵,教授,Email: zhanghan@scnu.edu.cn. TN929.5 A 1000-5463(2016)03-0088-05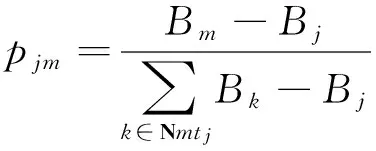
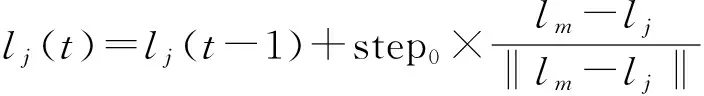
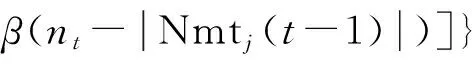

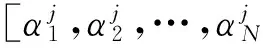
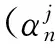
2 结果与讨论



3 结论
