基于零水印和可逆水印的矢量地图多重水印算法

曹　阳， 肖　菁， 张文才

(华南师范大学计算机学院，广州 510631)



基于零水印和可逆水印的矢量地图多重水印算法

曹阳， 肖菁*， 张文才

(华南师范大学计算机学院，广州 510631)

为实现对高保真矢量地图的版权保护，提出了一种基于零水印和可逆水印的矢量地图多重水印算法.该算法根据网格密度和属性熵值对矢量地图结点进行空间聚类，选取各集簇的密度中心点嵌入零水印，相对距离特征点嵌入可逆水印.其中，水印信息进行Arnold置乱以保障其安全性；零水印采用改进的零比特动态扩展方法，只对特征点的x或y坐标嵌入水印，在减少所需特征点数量的同时，提高对精度约减攻击的抵抗能力；可逆水印采用改进的差值扩展和平移算法，对不同差值区间的结点采用不同的水印嵌入方法，以提高水印容量，并通过x或y坐标独立嵌入水印信息，以降低水印对地图精度的影响.实验结果表明，基于零水印和可逆水印的多重水印方案能够较好地解决矢量地图精度和水印鲁棒性之间的矛盾，相对于单值水印算法具有更高的抗攻击能力，适用于矢量地图在高保真场合下的版权保护.

矢量地图； 多重水印； 零水印； 可逆水印； 鲁棒性

矢量地图数据具有结构紧凑、冗余度低和显示精度高等特点，是当前网络空间信息发布和共享的主流数据格式之一[1].由于其制作成本高、数据量大且易被非法复制、篡改和传播等，矢量地图的版权保护问题逐渐成为地图安全防护研究的焦点.

数字水印技术是解决数字地图版权问题的关键技术之一.相对于栅格图像的水印算法而言，矢量地图的数字水印算法研究成果较少.而且由于矢量地图数据在数据结构、存储形式、表现方式、应用环境、使用要求以及可能的攻击行为等方面与栅格地图数据都不一样，一般的图像数据水印算法很难直接应用在矢量地图数据上[2].目前，矢量图形水印算法主要分为频域算法和空域算法[3].这2种算法在嵌入数字水印时均不可避免地对地图数据进行改动，从而有损空间数据的精度，影响矢量地图的正常使用.为了减少对地图数据精度的损伤，学者们提出了零水印和可逆水印技术.

零水印不会修改原始作品的内容[4].张佐理等[5]提出了矢量地图的零水印算法，该方法构造较为简单，算法抵抗各类攻击的能力较差.文献[3, 6-11]选取不同的地图特征点嵌入水印信息，以提高算法的鲁棒性.但在不引入第三方认证的前提下，目前的算法抵抗解释攻击的能力较弱.

可逆水印信息的嵌入对载体数据产生一定扰动，但在水印信息提取的同时，可同步消除这种数据扰动，恢复地图的原始数据[12]、VOIGT等[13]最早提出矢量地图的可逆水印算法，但该算法嵌入水印的容量较小. WANG等[14]采用差值扩展方法实现了矢量地图的可逆水印，但为了实现可逆恢复，需要记录较多的定位信息.文献[15-17]改进了差值扩展方法，结合差值平移技术，可以不存储定位图，且提高了水印的嵌入率.

零水印和可逆水印虽然有效地降低了矢量地图精度损失，但单值水印嵌入的容量和鲁棒性往往不高.为了解决这一问题，本文采用了多重水印的方案.多重水印是指用不同方法在同一种介质中嵌入一个或多个水印的技术.目前国内外的多重水印研究主要针对图像和音频数据，对于数字地图的研究相对较少[18].文献[18-19]提出了GIS矢量数据多重水印嵌入方法，但不能同时兼顾矢量数据的精度.为了解决矢量地图精度和水印鲁棒性之间的矛盾，本文提出了1个基于零水印和可逆水印的多重水印算法，每个嵌入的水印都有不同的特征点空间，克服了单一水印的不足，对矢量地图高保真场合下的版权保护具有很高的适用性.

1　多重水印方案

1.1水印信息的生成

为增强水印信息的安全性，首先将含有版权信息的原始水印图像进行Arnold置乱操作[20]，得到一个二值水印序列:

图1　水印图像置乱示例

Arnold变换具有周期性，即对图像进行一定次数的Arnold变换后，能够重新得到原始图像.因此，可以在需要提取水印时，采用Arnold反置乱，即可获得原始水印图像.

1.2特征点的选取

根据数字矢量地图的空间特征，选择关键性的地图特征结点来嵌入数字水印信息，不但可以增强数字水印算法的稳健性，而且对于剪切操作具有很好的抵抗能力.为了提高水印的鲁棒性，本文采用结合矢量地图属性特征的空间聚类分析方法[12]50，分别选取嵌入零水印和可逆水印的特征点空间，其处理步骤如下：

第1步，根据矢量地图中点、线、多边形的基本拓扑结构，设定各结点的密度熵值和属性熵值.其中，密度熵值反映了结点区域的点密集程度，而属性熵值描述了结点的重要性，例如孤立点的属性熵值最大；线上端结点熵值大于线中其他各结点；多边形各结点的熵值相等.

第2步，根据地图的结点数量和分布情况，计算出地图的平均属性密度阈值Davg：

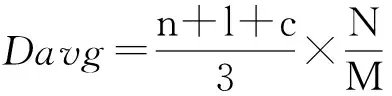
其中，n、l、c分别代表孤立结点、线结点和多边形结点的属性熵值，N为结点数量，M为网格数.

第3步，在属性密度阈值的约束下，对矢量地图中所有结点进行聚类.对于每个集簇，选取密度差异值最小的结点为集簇的密度中心.密度差异值的定义如下：

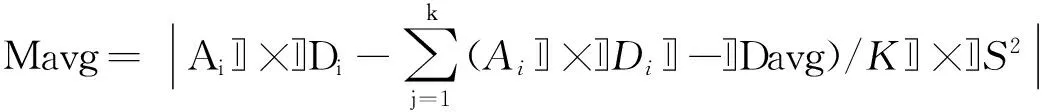
其中，Mavg为密度差异值，Di代表结点i的密度熵值，Ai代表结点i的属性熵值，Davg为平均属性密度熵值，K为集簇内结点总数，S代表网格步长.

第4步，按照距离度量方式计算集簇内各结点到密度中心的相对距离：

其中P代表待选择结点，C为该集簇内的密度中心点，Ai代表结点i的属性熵值.

第5步，选取各集簇内的密度中心点作为零水印嵌入的特征点，符合Distance(P,C)≤ε(ε为相对距离阈值)的结点作为可逆水印嵌入的特征点.

1.3基于零比特动态扩展的零水印算法

零比特动态扩展技术是一种实现矢量地图零水印算法的常用技术手段，其核心思想是将数字水印信息转化为零比特值，将其扩展到部分结点的坐标值末尾，从而保证结点的地理坐标值无变化.但理论分析表明该技术对于精度约减、坐标系转换等操作的抵抗能力较弱[9].

针对这一问题，本文提出了改进的零比特扩展方案：对于水印序列W=〈w1,…,wn〉，如果水印信息位wi…wi+j为1个或多个连续的“0”，则在特征点x坐标值后添加相应个数的“0”；如果水印信息位wi…wi+j为1个或多个连续的“1”，则在特征点y坐标值后添加相应个数的“0”.

图2给出了零比特扩展方案的示例，将长度为8的水印序列“11010111”嵌入到矢量地图的特征点坐标中.该方案对连续的0或1一起嵌入到坐标中，从而减少了所需特征点的数量.另一方面，只对特征点的x或y坐标嵌入水印，增加了精度约减攻击的难度和代价.

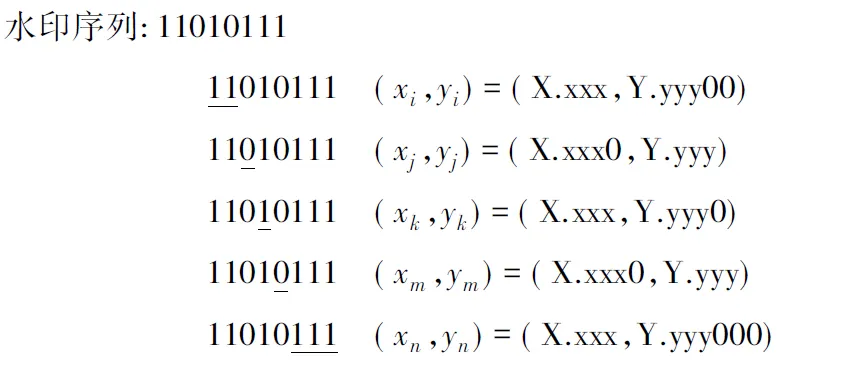
图2改进的零比特扩展编码规则示例

Figure 2A example of the improved zero-bit dynamic extension rules

1.4基于差值扩展和平移的可逆水印算法

传统的差值扩展和平移算法[15]对于差值绝对值大于阈值的顶点对不能嵌入水印，从而影响水印的嵌入量；如果通过增加阈值来提高水印容量，又会引起较大失真.为了解决这一矛盾，本文在文献[17]的工作基础上提出了改进的差值扩展和平移的可逆水印算法，一方面对不同类型的结点采用不同的水印嵌入方案，以提高水印容量；另一方面只对特征点的x轴坐标和y轴坐标嵌入水印，可以减少地图的失真.其水印嵌入流程如下：

第2步，将所有相邻2个结点两两组合为结点对，按照

mxi=；

和

myi=

计算这些结点对整数二进制坐标之间的均值mxi、myi和差值dxi、dyi，其中」表示向下取整操作.其逆变换为：

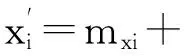
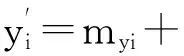
第3步，将差值dxi与设定的阈值k进行比较后，按以下2种情况分不同区间嵌入水印信息wi：

当i为偶数时，为

(1)

当i为奇数时,为

(2)

嵌入水印信息后，特征点生成新的坐标值：

当i为偶数时，为

(3)

当i为奇数时，为

(4)

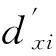
1.5多重水印的嵌入流程

多重水印要达到能够同时抵抗多种攻击的鲁棒性，重点在于不同水印嵌入特征点的空间关系.本文的多重水印嵌入方案以1.2节介绍的地图结点空间聚类为基础，将特征点集划分成2个可重现的不相交子集：在各集簇的密度中心点嵌入零水印信息，可以降低对地图精度的扰动；在距离中心点ε范围之内的特征点嵌入可逆水印信息，可以提高水印的嵌入容量和鲁棒性.多重水印的嵌入流程如图3所示.

图3　多重水印嵌入流程

水印信息W1和W2先后嵌入到矢量地图中的密度中心结点和相对距离特征点，保证所有顶点都只在精度范围内修改一次，使保真性得到了控制.当一种水印受到某种攻击时，可以通过嵌入另一个水印的特征点提取出相应的水印信息，从而提高了水印的鲁棒性.零水印在精度约减和解释攻击下的脆弱性，也因为可逆水印的加入得到了极大的降低.

2　实验结果分析

本文对矢量地图的水印算法进行评测，采用的指标是归一化均方差NMSE[21]和相似度sim[22]：

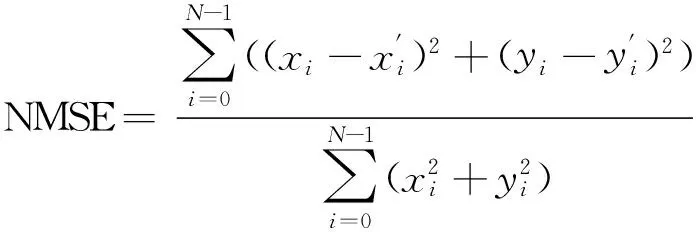
实验数据选择广东省县市级行政区划和中国省级行政区划的2幅SVG矢量地图(图4).

图4　待嵌入水印的矢量地图

首先进行水印的嵌入和提取实验，分别对2幅SVG矢量地图嵌入本文改进的零水印、可逆水印和多重水印，计算NMSE值评价地图精度降低的程度.提取水印后，计算原始水印和提取出水印信息的相似度sim.

由实验结果(表1)可以看出，零水印的嵌入不会影响地图精度，水印提取效果最好.可逆水印可以通过设置阈值k来控制嵌入水印后地图的失真程度，而提取水印与原始水印稍有偏差的原因在于嵌入和提取水印运算中」和「取整运算引入的误差.多重水印的提取效果略逊于2个独立水印算法是因为嵌入水印后结点坐标发生改变，导致提取水印时计算各集簇的密度中心点和相对距离特征点发生偏差.但多重水印对矢量地图精度的影响和水印提取效果均在可控和可接受范围之内.

表1　水印的嵌入和提取实验结果

接下来的实验是测试各水印算法在精度约减和裁剪攻击下的鲁棒性，这里主要以计算提取水印和原始水印的相似度sim作为评测指标.

首先进行精度约减(即结点坐标小数点后有效位数压缩一位)实验.因为零水印对精度约减操作的抵抗能力最弱，因此重点分析本文的零水印算法和多重水印算法的鲁棒性. 由表2的实验结果可看出，嵌入零水印的地图进行精度约减操作后，水印提取的效果不好，不过本文提出的零水印方案鲁棒性优于文献[12]46中的零水印算法.而多重水印算法由于多嵌入了一个可逆水印，水印对精度约减操作的鲁棒性变强.

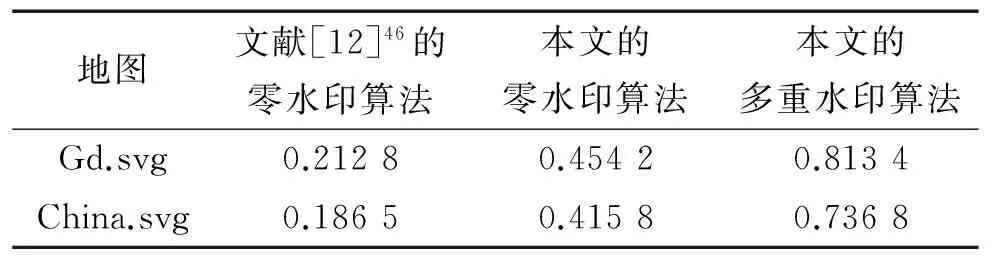
表2　精度约减后的sim计算结果

最后进行裁剪攻击实验，分别在矢量地图中嵌入本文提出的零水印、可逆水印和多重水印之后，对地图进行不同程度的裁剪(图5)，图5A～D是对Gd.svg进行裁剪后的部分地图，图5E～H是对China.svg进行裁剪后的部分地图，对裁剪后的地图进行水印检测.

图5　裁剪攻击后的矢量地图

由表3可以看出，在裁剪攻击之下，相比于单一的水印算法，多重水印方案在地图中嵌入了2个水印的信息，因此提取出的水印效果更好，具有较好的鲁棒性.在可以使其他单一水印失效的裁剪攻击下(设定可接受水印相似度阈值的simmin=0.6)，例如图5D和图5H，多重水印的提取依然有效.

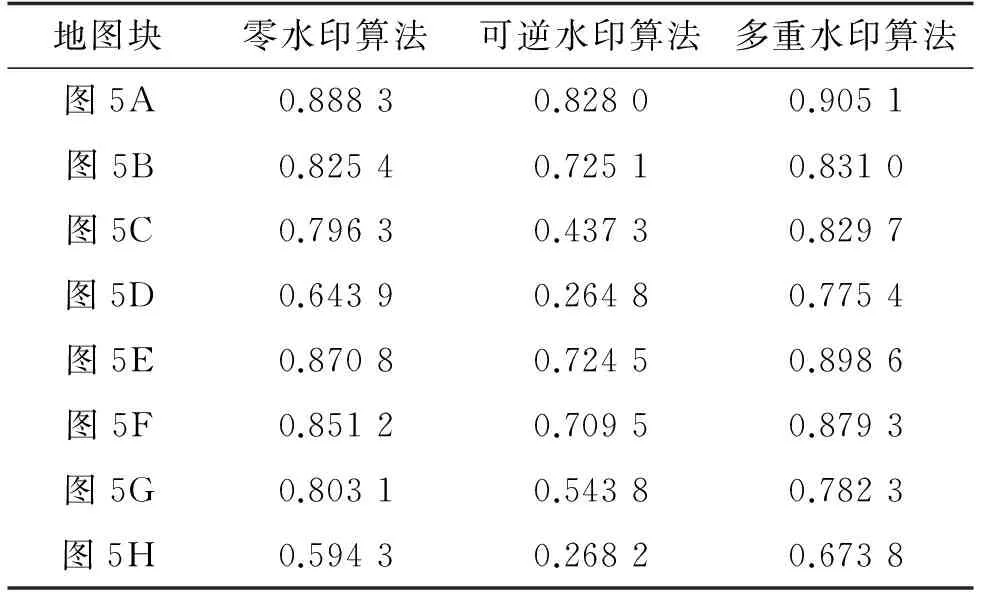
表3　裁剪攻击下的sim计算结果

3　结束语

本文以矢量地图为研究对象，探讨如何使用数字水印技术对矢量地图进行版权保护.从工程应用中对矢量地图高精度要求为出发点，提出了一种能够在高鲁棒性的情况下保持较高精度的多重水印算法.该多重水印采用了零水印和可逆水印技术，其中零水印算法具有不对精度造成任何影响的特点，而可逆水印算法在提取水印的同时可以对矢量地图进行数据还原.实验结果证明，本文的多重水印方案具有较好的鲁棒性，而且能把矢量地图精度的降低幅度控制在一定的阈值之内，适用于高保真场合下矢量地图的版权保护.

[1]何文广. 一种强抗压缩的矢量地图数据盲水印算法[J]. 计算机与现代化, 2012(5):7-9;13.

HE W G. A strong anti-compression blind watermarking algorithm for vector map data[J]. Computer and Modernization, 2012(5):7-9;13.

[2]曾端阳,闫浩文,牛莉婷,等. 矢量地图的一种非盲数字水印算法[J]. 兰州交通大学学报, 2013，32(4):176-180.

ZHENG D Y, YAN H W, NIU L T, et al. A non-blind digital watermarking algorithm for vector map data[J]. Journal of Lanzhou Jiaotong University, 2013,32(4):176-180.

[3]孙鸿睿, 朱建军, 李光强,等. 一种基于矢量地图要素编码的零水印算法[J]. 工程勘察, 2012(9):54-57.

SUN H R, ZHU J J, LI G Q, et al. A zero-watermarking algorithm for vector map based on element coding[J]. Geotechnical Investigation & Surveying,2012(9):54-57.

[4]温泉,孙锬锋,王树勋.零水印的概念与应用[J].电子学报,2003,31(2):214-216.

WEN Q, SUN Y F, WANG S X. Concept and application of zero-watermark[J]. Acta Electronica Sinica, 2003, 31(2): 214-216.

[5]张佐理, 孙树森, 汪亚明，等. 二维矢量数字地图的零水印算法[J]. 计算机工程与设计, 2009,30(6):1473-1476.

ZHANG Z L, SUN S S, WANG Y M, et al. Zero-watermarking algorithm for 2D vector map[J]. Computer Engineering and Design, 2009, 30(6):1473-1476.

[6]LI A, LIN B X, CHEN Y, et al. Study on copyright authentication of GIS vector data based on zero-watermarking[C]∥The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences.Beijing:[s.n.], 2008:1783-1786.

[7]DU Q Z, PENG F. A zero-watermark algorithm with real-mean for 2D engineering graphic[C]∥International Symposium on Electronic Commerce and Security.Guangzhou:IEEE, 2008:890-893.

[8]孙鸿睿, 朱建军, 尹鹏程,等. 一种基于矢量地图特征点和分块的零水印算法[J]. 地理与地理信息科学, 2012,28(4):111-112.

[9]孙鸿睿. 矢量地图无损数字水印技术和算法研究[D]. 长沙:中南大学, 2013.

SUN H R. Study on lossless digital watermarking technology and algorithm for vector map[D].Changsha:Central South University, 2013.

[10]WANG X, HUANG D, ZHANG Z. A robust zero-watermarking algorithm for vector digital maps based on statistical characteristics[J]. Journal of Software, 2012, 7(10):2349-2356.

[11]WANG X, HUANG D J, ZHANG Z Y. A robust zero-watermarking algorithm for 2D vector digital maps[M]∥HE X G, HUA E, LIN Y, et al. Computer,informatics,cybernetics and application. Netherlands: Springer, 2012:533-541.

[12]孙建国. 基于内容特征的二维矢量地图数字水印术研究[D]. 哈尔滨:哈尔滨工程大学, 2009.

SUN J G. Research on digital watermarking of 2D vector map based on content feature[D]. Harbin:Harbin Engineering University, 2009.

[13]VOIGT M, YANG B, BUSCH C. Reversible watermarking of 2D-vector data[C]∥Proceeding of the 2004 Workshop on Multimedia and Security.New York:ACM, 2004.

[14]WANG X T, SHAO C Y, XU X G, et al. Reversible data-hiding scheme for 2-D vector maps based on difference expansion [J]. IEEE Transactions on Image processing, 2007, 2(3):311-320.

[15]武丹，汪国昭. 基于差分扩张和平移的2D矢量地图的可逆水印[J]. 光电子·激光，2009, 20(7):934-937.

WU D, WANG G Z. Reversible digital watermarking scheme for 2D vector maps based on difference expansion and shifting[J]. Journal of Optoelectronics·Laser，2009, 20(7): 934-937.

[16]孙鸿睿, 李光强, 朱建军,等. 改进的差值扩张和平移矢量地图可逆水印算法[J]. 武汉大学学报(信息科学版), 2012(8):1004-1007.

SUN H R, LI G Q, ZHU J J, et al. Improved reversible watermarking algorithm for vector map based on difference expansion and shifting[J]. Geomatics and Information Science of Wuhan University, 2012(8):1004-1007.

[17]丁璐, 裘正定, 章春娥. SVG矢量图的大容量可逆水印算法[J]. 计算机安全, 2010(5):24-26.

DING L, QIU Z D. ZHANG C E. Reversible watermarking algorithm of SVG vector graph′s high capacity[J]. Network and Computer Security, 2010(5): 24-26.

[18]魏春蕾. GIS矢量数据多重水印算法研究[D]. 兰州:兰州交通大学, 2014.

WEI C L. An multiple watermarking algorithm for GIS vector data[D]. Lanzhou:Lanzhou Jiaotong University, 2014.

[19]曹江华. GIS矢量数据多重水印研究[D]. 南京:南京师范大学, 2011.

CAO J H. Research on multiple watermarking for GIS vector data[D]. Nanjing:Nanjing Normal University, 2011.

[20] ARNOLD V I, AVEZ A. Ergodic problems of classical mechanics[M]. New York: W A Benjamin, Inc, 1968:124.

[21]KHALED E. Advances and innovations in systems, computing sciences and software engineering[M]. Netherlands: Springer, 2007:544.

[22]LI S S, ZHOU W, LI A B. Image watermark similarity calculation of GIS vector data[J]. Procedia Engineering, 2012,29:1334.

【中文责编：庄晓琼英文责编：肖菁】

A Multiple Watermarking Algorithm for Vector Map Based on Zero-Watermark and Reversible Watermark

CAO Yang， XIAO Jing*， ZHANG Wencai

(School of Computer Science, South China Normal University, Guangzhou 510631, China)

A multiple watermarking algorithm of vector map is proposed to achieve the copyright protection with the high-precision requirement. This algorithm uses two types of watermarks: zero-watermark and reversible watermark. First, the vertices are clustered according to the mesh density and the attribute entropy. The density center points are chosen to embed the zero-watermark bits, and the feature points within a relative distance to the center are applied to identify regions for the reversible watermark insertion. Then, the copyright watermark image is scrambled with Arnold transformation to improve security. And in the zero-watermarking scheme, the improved zero-bit dynamic extension algorithm is used to modify only thex(ory) coordinate values of the center points, which will need less points to embed the copyright information and also can improve robustness against precision reduction. In the reversible watermarking scheme, the improved difference expansion and shifting algorithm is used. Different reversible watermarking formulas are applied to different interval points to embed a high capacity reversible watermark. Only thex(ory) coordinate values of the feature points are hided copyright information to reduce the effect of the map on quality. The experimental results show that the proposed multiple watermarking algorithm can better solve the contradiction between vector map accuracy and watermark robustness.The multiple watermarking scheme based on zero-watermark and reversible watermark has better attack resistance than single watermarking scheme,which is eligible for copyright protection of vector map with high data precision requirement.

vector map; multiple watermark; zero-watermark; reversible watermark; robustness

2016-04-13《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(61202296)；广东省自然科学基金项目(S2012030006242)

肖菁，教授，Email: xiaojing@scnu.edu.cn.

TP309

A

1000-5463(2016)03-0069-06