结构位移对受电弓气动抬升力的影响分析

林泽峰, 杨翊仁

(西南交通大学力学与工程学院, 成都　610031)



结构位移对受电弓气动抬升力的影响分析

林泽峰, 杨翊仁

(西南交通大学力学与工程学院, 成都610031)

为了研究受电弓结构位移对其气动特性的影响，利用流体分析软件Fluent，基于三维定常不可压缩流和标准k-ε两方程湍流模型，对运行速度300 km/h下受电弓所处的有限个结构位移状态下各部件的气动力进行数值模拟。建立受电弓气动抬升力的简化计算模型，推导气动力转化为气动抬升力的传递系数。结果表明：受电弓气动抬升力的传递系数与其工作高度有关；在受电弓从初始工作高度1.5 m抬升至1.6 m的过程中，整弓气动抬升力值随升弓高度的增大而减小。

受电弓；结构位移；气动特性；抬升力

引　言

弓网受流稳定性和安全性一直是电气化铁路研究的一个重要课题。随着列车运营速度的提升，气动力对弓网耦合振动的不利影响愈发明显。目前国内外学者对受电弓气动力的研究[1]主要为数值仿真[2-3]、风洞试验[4-5]和线路试验等[6-7]。对弓网系统振动响应的研究大多局限于单向流固耦合[8-9]的分析方法。由文献[5]可知，机车运行速度为80 km/h时升弓角变化5°可导致气动升力30%和气动阻力50%的变化。此类方法不考虑结构位移(升弓角保持不变)，仅能在一定程度上反映空气动力对弓网耦合振动的影响，且气动力的获取与受电弓结构自身的运动状态无关。

本文建立受电弓气动抬升力的简化计算模型[10]，考虑受电弓升弓角的变化，给出工作高度变化为0.1 m的范围内各主要部件气动抬升力传递系数随工作高度变化的规律。利用流体仿真软件Fluent计算在该范围内变化的工作高度下受电弓各部件的气动升、阻力，最终分析得出整弓气动抬升力随其工作高度(或升弓角)的变化规律。

1　受电弓气动抬升力计算模型及求解

受电弓实体结构较为复杂，由下臂杆、上框架、拉杆和弓头组成一个四连杆机构，杆件之间通过铰接相连，如图1所示。弓头在平衡杆牵拉下，实现滑板在受电弓运行过程中保持水平。由于拉杆和平衡杆所受气动力较小，为简化计算，仅考虑受电弓下臂杆、上框架和弓头的气动力作用。

如文献[10]所述，受电弓在高速气流作用下，在弓头产生的垂向作用力(即气动抬升力)并非由各部件所受的气动升力和阻力简单叠加，而是各部件气动升、阻力和气动力矩共同作用的结果。对于受电弓给定的几何外形，各部件的气动升、阻力都将对整弓的气动抬升力造成影响，并通过气动抬升力传递系数加以体现。

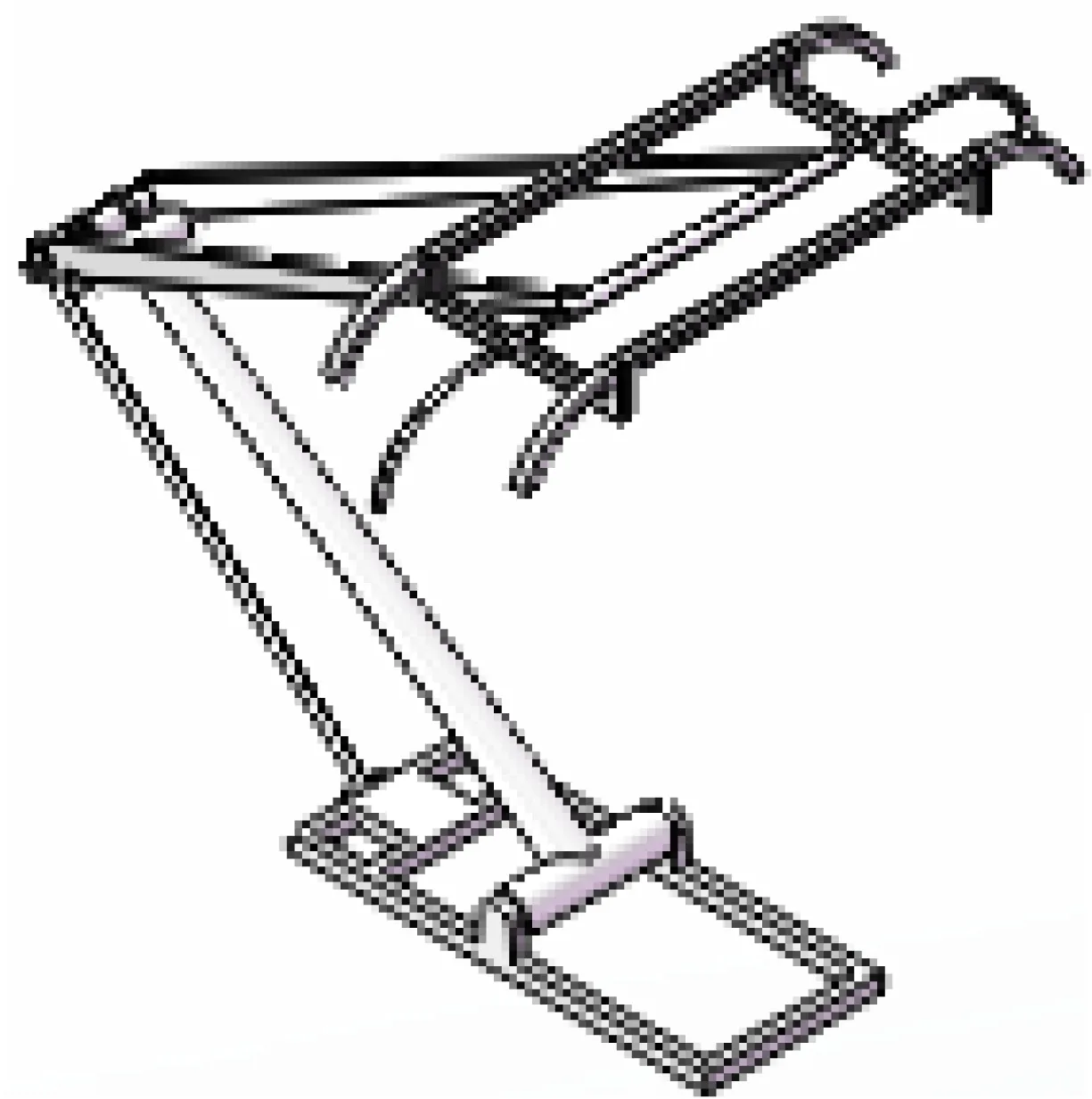
图1受电弓3D简化模型

受电弓气动抬升力的计算模型如图2所示。abc、be和cd分别为上框架、下臂杆和拉杆，弓头位置为a处；g和h分别为上框架和下臂杆气动力矩为零的点；L1、L2、L3、L4和L5分别对应线段ag、gb、bc、bh和he的长度；Fa、F1、F2、F3、F4、F5和F6分别对应整弓气动抬升力、弓头气动阻力、弓头气动升力、上框架气动阻力、上框架气动升力、下臂杆气动阻力和下臂杆气动升力。

图2受电弓气动抬升力计算模型

由文献[10]的推导给出如下结论：

(1)

令La=L1+L2，Lb=L4+L5，各参数可表示为

A=Lasinαsin(γ-θ)-L3sinθsin(β+γ)

(2)

B=L2sinαsin(γ-θ)-L3sinθsin(β+γ)

(3)

C=L2cosαsin(γ-θ)+L3cosθsin(β+γ)

(4)

D=-L3L5sinθsin(β+γ)

(5)

E=-L3L5cosθsin(β+γ)

(6)

M=Lacosαsin(γ-θ)+L3cosθsin(β+γ)

(7)

N=Lb[Lacosαsin(γ-θ)+L3cosθsin(β+γ)]

(8)

式(2)～式(8)中，角α、β和γ均可通过受电弓各杆件的几何关系表示为与θ相关的函数。由式(1)给出的结论可知，Α/M、1、Β/M、C/M、D/N和E/N分别对应弓头气动阻力、弓头气动升力、上框架气动阻力、上框架气动升力、下臂杆气动阻力和下臂杆气动升力的气动抬升力传递系数。

2　受电弓空气动力学模型

从气动弹性的观点来看，受电弓上的气动力与受电弓结构的位移相关，计算受电弓的气动弹性响应需要用到不同时刻的气动力。受到气流扰动作用，弓头、上框架和下臂杆为主要受力部件。受电弓各部件的非定常气动升、阻力可通过风洞实验测试获得，或通过流体仿真软件计算获取。本文基于Fluent建立受电弓气动力计算模型，如图3所示。受电弓初始工作高度选取为1.5 m，在受电弓工作高度抬升δ=0.1 m范围内，将抬升量δ进行6等分，分别对各部件的气动升、阻力进行计算，抬升量δ依次增加的过程中，受电弓气动力计算模型随着受电弓几何外形的改变而依次更新，以期近似获得受电弓上的非定常气动力。

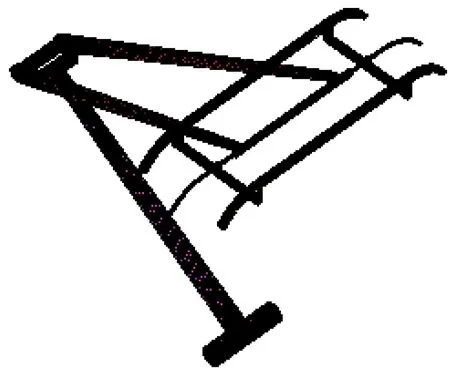
图3受电弓气动力计算模型

假定受电弓以恒定速度运行，忽略流场流动的不均匀性，受电弓周围空气视为定常、等温和不可压缩三维流场。考虑气流绕流和流场的充分发展，流场计算域选为长方体，湍流模型采用标准k-ε模型。来流方向X+和尾流方向X-为受电弓X方向宽度的5倍；横向Y+和Y-为受电弓Y方向宽度的5倍；高Z+为受电弓纵向高度的5倍。由于受电弓结构较为复杂且需多次改变结构几何形态重新建模，全流场采用非结构四面体网格并对受电弓附近区域网格局部加密。流场最外围网格尺寸为160 mm，受电弓表面网格尺寸为3 mm～8 mm，网格尺寸呈梯度变化。仅研究受电弓开口运行状态下的气动特性：计算域入口边界设置为速度入口，速度为300 km/h；出口边界设置为压力出口，初始压强为标准大气压；其余边界设置为无滑移壁面。

3　结果分析

3.1受电弓各部件的气动抬升力传递系数分析

受电弓工作高度为1.5 m时的几何外形参数见表1，初始工作高度为1.5 m时对应的升弓角θ为0.434弧度。由初始工作高度抬升至1.6 m的过程中，上框架和下臂杆气动力矩为零的点会产生微小变化，即L1、L2、L4和L5的取值会随之改变，考虑变化量较小，L1、L2、L4和L5的值统一取为初始工作高度处的数值。

表1　受电弓几何参数

α、β和γ的值随θ的变化(或随受电弓的工作高度)唯一确定，经计算给出α、β、γ和θ随受电弓工作高度变化的函数曲线。如图4所示，在δ=0.1 m的变化范围内，4个角度参量都随升弓高度的增加而增加，由于δ变化为小量，4个角度参量都近似呈线性增长。

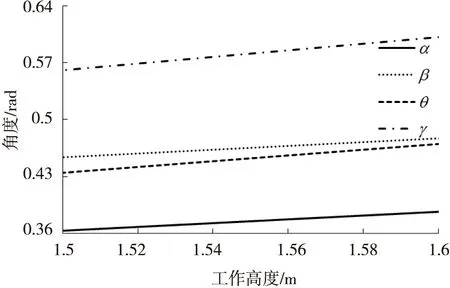
图4角度参量随升弓高度的变化

将基于表1参数和图2所示模型得出的计算结果代入式(1)～式(8)，可得受电弓各个工作高度下的气动力传递系数，见表2。气动力转化成气动抬升力的传递系数表征气动升、阻力对受电弓气动抬升力的贡献大小。从各传递系数的绝对值大小分析，气动升力传递系数的值都比其气动阻力的值大；各部件气动升力的传递系数受工作高度影响较小，气动阻力的传递系数受工作高度的影响则较大；弓头气动升力的传递系数除外，各部件气动阻力传递系数的绝对值随受电弓工作高度的增大而增大，气动升力传递系数的绝对值随受电弓工作高度的增大而减小。

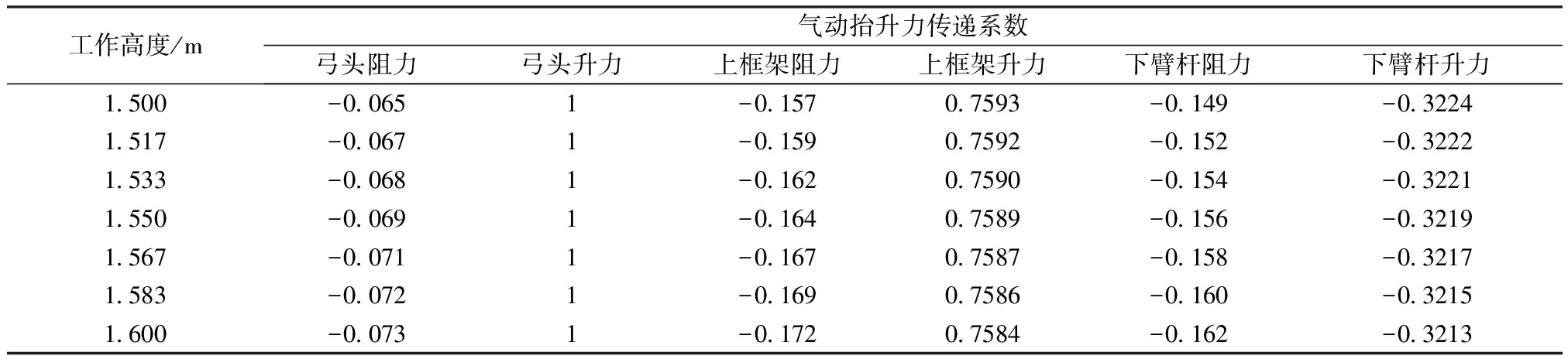
表2　受电弓各部件气动力传递系数

3.2受电弓各部件气动升力和气动阻力分析

在速度为300 km/h，工作高度为1.5 m的条件下，受电弓开口运行时各部件的气动升、阻力迭代计算情况如图5和图6所示，各部件的气动力数值在迭代600次左右呈平缓变化的趋势。

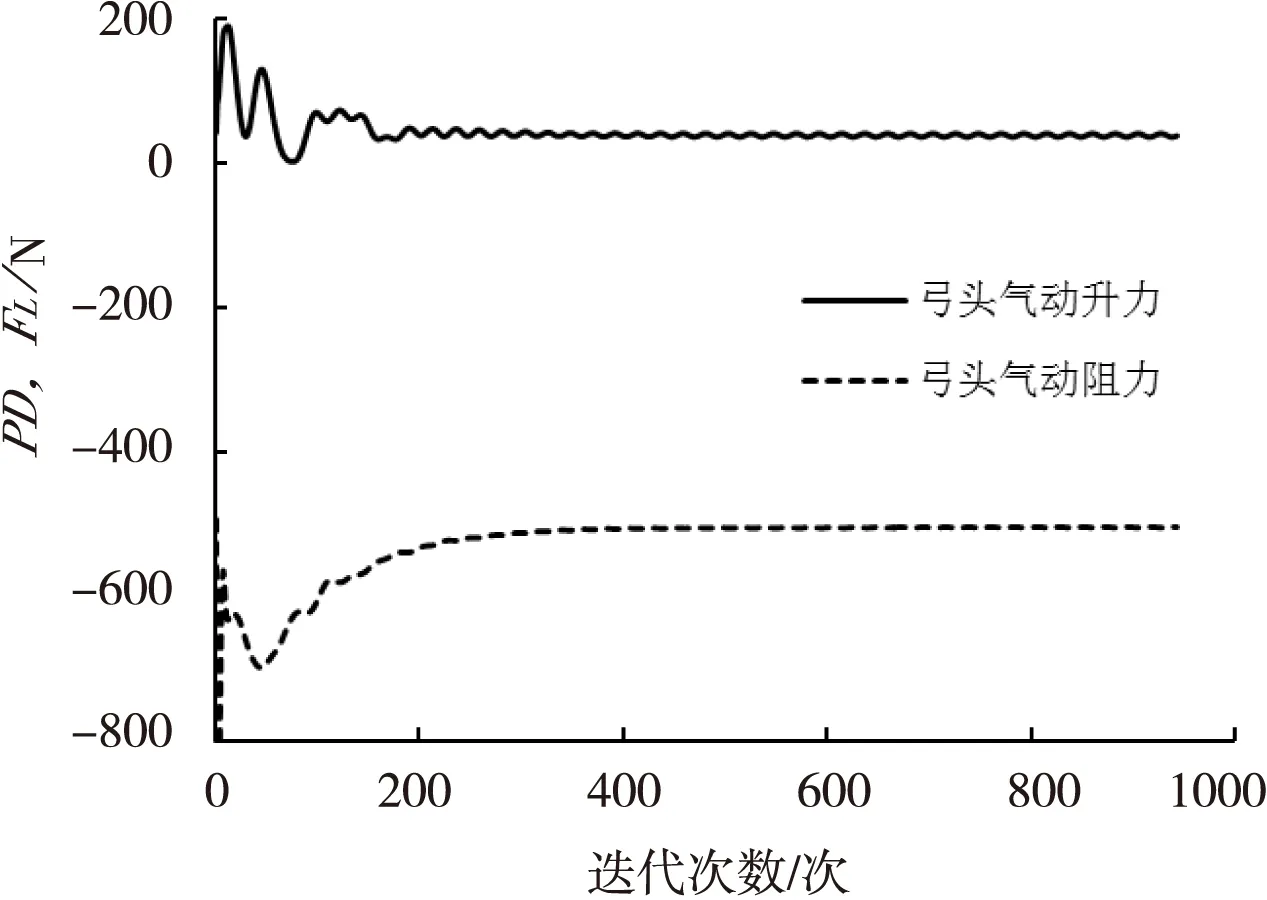
图5弓头气动升、阻力

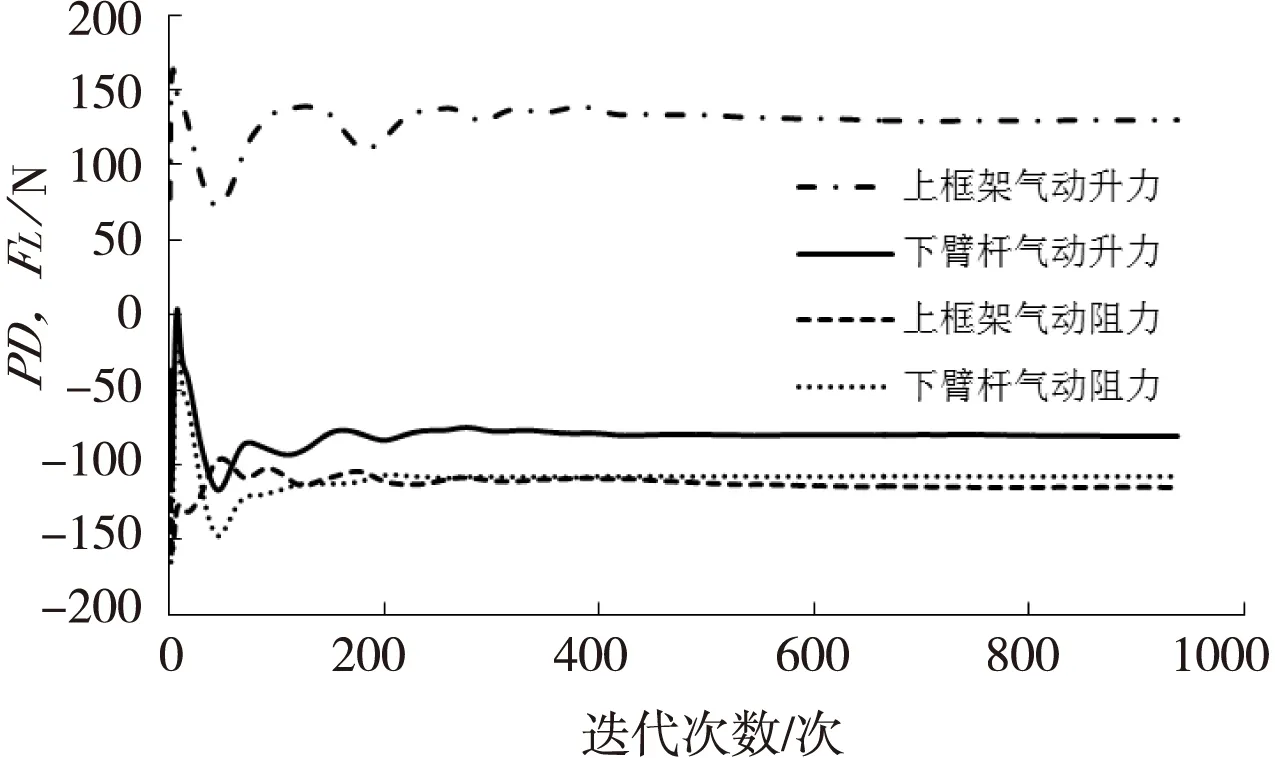
图6上框架和下臂杆气动升、阻力

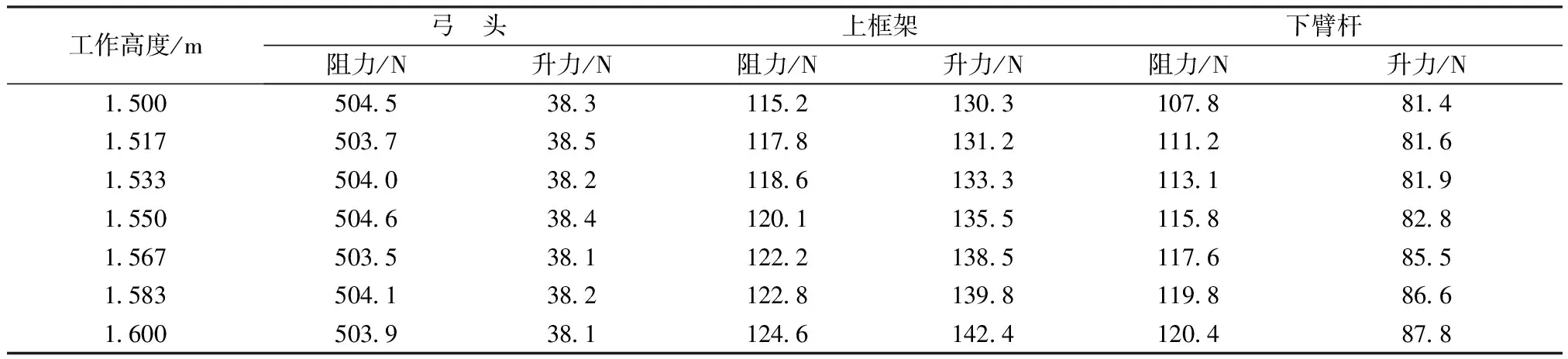
以受电弓工作高度1.5 m处为初始状态，工作高度抬升量递增至δ，对受电弓各部件的气动力数值重复计算，结果见表3。由表3可知，随着受电弓工作高度的变化，上框架和下臂杆的气动升、阻力数值也随之变化，其绝对值均随工作高度的增大而增大。弓头气动升、阻力数值受工作高度的变化影响较小。

3.3受电弓气动抬升力

综合表2气动抬升力传递系数和表3气动力数值，受电弓各部件气动力转化为气动抬升力数值的情况见表4。由表4可知：开口运行条件下，上框架和弓头的气动升力转化为受电弓气动抬升力的数值为正，即对受电弓的等效气动抬升力作用方向朝上，其余各部件气动力转化为气动抬升力的数值均为负；各部件气动升、阻力转化为气动抬升力的数值均不是小量，整弓气动抬升力是由各部件气动升、阻力和力矩共同作用的结果。

注：表中气动升、阻力正负取值参照图2的气动力加载情况，方向一致为正，反之为负。

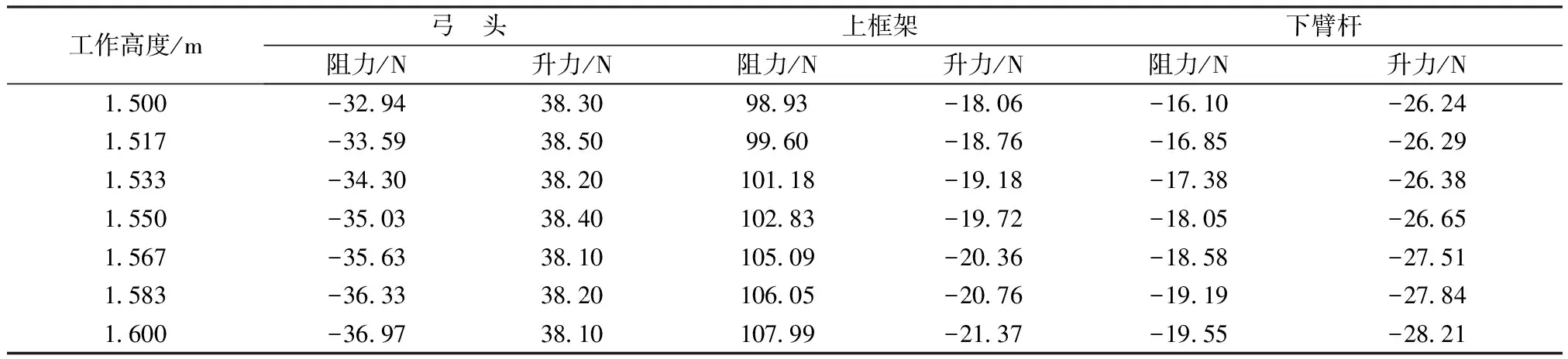
表4　受电弓各部件气动力转化为气动抬升力的数值

将受电弓各部件气动升力和阻力转化为气动抬升力的值区分开来，并结合整弓气动抬升力随受电弓工作高度的变化，结果如图7～图9所示。由图7～图9可知：受电弓气动升力转化为气动抬升力的合力值随工作高度的增大而增大；受电弓气动阻力转化为气动抬升力的合力值随工作高度的增大而减小；整弓气动抬升力数值为正值，并且随工作高度的增大而减小。

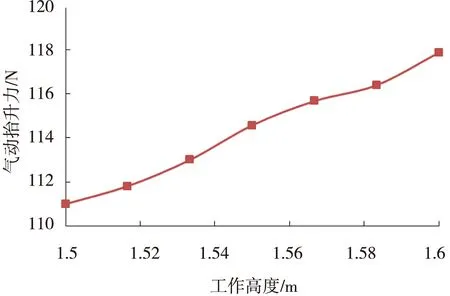
图7气动抬升力(升力)随工作高度的变化规律

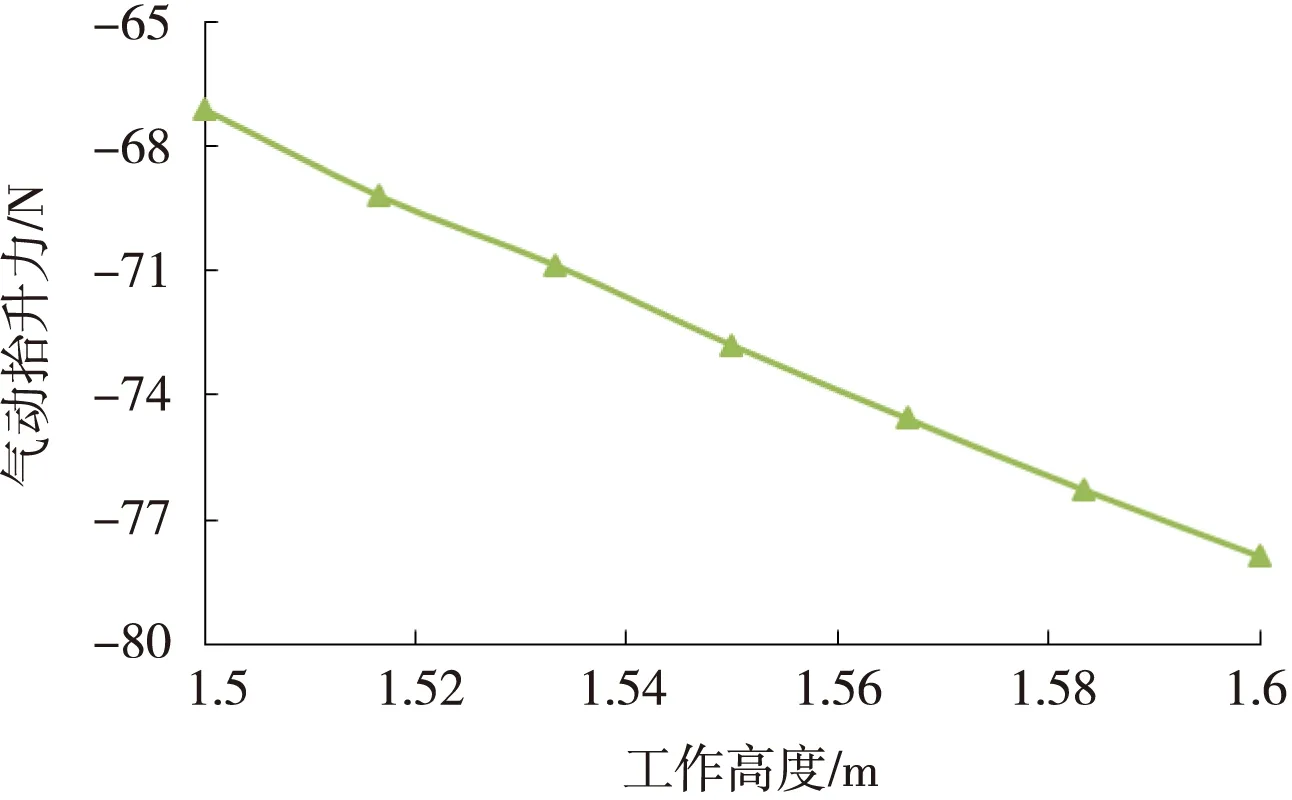
图8气动抬升力(阻力)随工作高度的变化规律

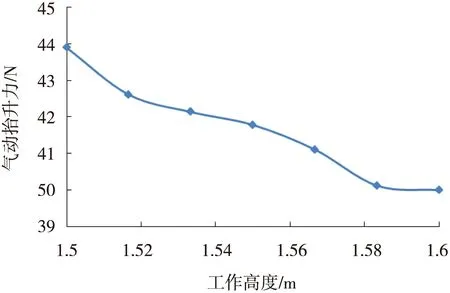
图9气动抬升力(整弓)随工作高度的变化规律

由于受电弓各部件气动升、阻力随工作高度变化而变化，而气动力传递系数也由其工作高度所决定，因此整弓气动抬升力的值为关于其工作高度的函数。近似地，在工作高度变化δ=0.1 m的范围内，升弓角θ变化仅为2.3°，气动抬升力变化范围仅为4 N，由图9变化趋势可视为线性变化。采用该方式描述的受电弓气动抬升力在弓网耦合振动响应计算中能从一定程度上反映气动力与结构自身运动状态的关系。

4　结束语

根据受电弓气动力转化为气动抬升力传递系数的计算结果可知，受电弓的几何设计参数和受电弓的工作高度(或升弓角)影响其气动抬升力传递系数的值。

受电弓由初始工作高度(1.5 m)抬升0.1 m的过程中，整弓气动抬升力随工作高度的增大而减小，因此受电弓自身结构外形的改变是影响其气动抬升力数值变化的重要因素。

[1] 张静,刘志刚,鲁小兵,等.高速弓网空气动力学研究进展[J].铁道学报,2015(1):7-15.

[2] BOCCIOLONE M,RESTA F,ROCCHI D,et al.Pantograph aerodynamic effects on the pantograph-catenary interaction[J].Vehicle System Dynamics,2006,44(S1):560-570.

[3] POMBO J,AMBROSIO J,PEREIRA M,et al.Influence of the aerodynamic forces on the pantograph-catenary system for high-speed trains[J].Vehicle System Dynamics,2009,47(11):1327-1347.

[4] 杨海泳.高速受电弓风洞试验报告[R].成都:西南交通大学轨道交通国家实验室(筹),2011.

[5] 张弘,于正平,吴鸿标.受电弓空气动力学模型及风洞试验研究[J].中国铁道科学,1995,16(1):37-49.

[6] 张卫华,梅桂明,周宁.京沪先导段受电弓气动特性试验报告[R].成都:西南交通大学轨道交通国家实验室(筹),2011.

[7] 张冰,刘会平,韩通新.气动力作用对弓网受流影响的研究分析[J].铁道机车车辆,2012,32(3):132-135.

[8] 杨康,黄焯麒,于龙,等.受电弓空气动力对列车弓网特性的影响仿真[J].计算机工程与设计,2014,35(11):3933-3937.

[9] 刘星,邓见,郑耀,等.高速列车受电弓空气动力学对弓网受流的影响[J].浙江大学学报:工学版,2013,47(3): 558-564.

[10] 李瑞平,周宁,张卫华,等.受电弓气动抬升力计算方法与分析[J].铁道学报,2012(8):26-32.

Analysis on Effects of Structural Displacement on Pantograph’s Aerodynamic Uplift Force

LINZefeng,YANGYiren

(School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China)

To study the effects of pantograph’s structural displacement on its aerodynamic characteristics, the fluid analysis software FLUENT was used to simulate the aerodynamic forces acting on the pantograph with limited number of pantograph’s structural displacement state with running speed of 300 km/h based on three-dimensional steady incompressible flow and standardk-eturbulence model. The aerodynamic uplift force simplification model of pantograph was established, and the transfer coefficients for the aerodynamic forces converted into the aerodynamic uplift forces was derived. The results show that the transfer coefficients for pantograph’s aerodynamic uplift forces are related to working height; when pantograph’s working height rising from initial 1.5 m to 1.6 m, the pantograph’s full aerodynamic uplift force is decreased with the increase of pantograph’s working height.

pantograph; structural displacement; aerodynamic characteristic; uplift force

2016-03-20

国家自然科学基金(11372258)

林泽峰(1991-),男,福建厦门人,硕士生,主要从事流固耦合方面的研究,(E-mail)15202897197@163.com;

杨翊仁(1959-),男,教授,博士,主要从事流固耦合方面的研究,(E-mail)yangyiren05@126.com

1673-1549(2016)03-0070-05

10.11863/j.suse.2016.03.15

U264.3+4

A