高阶剪切理论下梯度直梁在热环境中的静动态响应分析
2016-11-04常学平成志强柳葆生
常学平, 成志强, 柳葆生
(1.西南石油大学机电工程学院, 成都 610500;2.西南交通大学力学与工程学院, 成都 610031)
高阶剪切理论下梯度直梁在热环境中的静动态响应分析
常学平1,2, 成志强2, 柳葆生2
(1.西南石油大学机电工程学院, 成都610500;2.西南交通大学力学与工程学院, 成都610031)
基于高阶剪切变形梁理论研究了两端不可移简支功能梯度梁在横向非均匀升温下的热屈曲和自由振动问题。首先依据高阶剪切变形梁理论和Hamilton原理建立了功能梯度梁受热-机载荷共同作用下的几何非线性动力学控制方程;在研究静态热屈曲问题时,把方程退化成强非线性边值问题,采用打靶法数值求解该边值问题,获得了横向非均匀升温下梁的屈曲构型,绘出了梁的变形随温度载荷及材料梯度参数变化的特征关系曲线;研究动态响应时,采用Navier方法数值求解所建立的动力学控制方程,获得了横向非均匀升温下梁的自由振动响应,数值比较了不同剪切理论下梁的前3解固有频率随跨高比、材料梯度参数变化的规律。结果表明,剪切变形、梁的跨高比、材料的非均匀性、温度变化对于高阶剪切功能梯度材料梁的变形及固有频率有很显著的影响。
高阶剪切变形理论;功能梯度材料梁;热屈曲;横向非均匀升温;自由振动
引 言
功能梯度材料(Functionally Graded Materials, FGMs)是一种新型非均匀复合材料,它以连续梯度变化的材料组分来代替传统复合材料的突变界面,消除了物理性能的突变,因而可较好地避免或降低应力集中现象[1-2]。因此,FGMs在核反应堆、航空航天、内燃机、激光加热等工程领域中具有潜在的应用前景[1-3],其结构在热载荷下的力学行为研究已成为固体力学一个活跃的研究方向[4-6]。
目前,对传统复合材料梁以及功能梯度Euler梁和功能梯度Timoshenko梁、板在热载荷作用下的静、动态力学理论和数值分析已有一些研究成果。Sankar等[7]基于弹性力学基本理论推导出了FGM Euler梁的位移、应力的简化表达式;Chakraborty等[8]采用有限元法分析了具有FGM过渡层的Timoshenko夹层梁的弯曲和振动;Bhangale等[9]利用有限元法研究含有粘弹性层的功能梯度梁在热环境下的屈曲与振动;Khdeir和Reddy[10-12]使用状态空间法,研究了层合梁在经典梁理论、一阶剪切梁理论、高阶剪切梁理论下的弯曲行为,获得了各种边界条件下精化梁的振动频率和临界屈曲载荷;夏贤坤和沈惠申[13]基于Reddy高阶剪切变形理论和广义von Karman型方程分别研究了FGM板和混杂铺设的层合板在热屈曲前和热过屈曲状态的非线性自由振动响应,给出了频率与温度载荷的特征曲线;Zhu等[14]提出了求解在正弦分布力作用下,弹性模量沿厚度任意分布的FGM梁弯曲响应的Fourier-Galerkin法;李世荣等[15]研究了材料性质沿厚度按幂函数变化的功能梯度材料Timoshenko梁的热过屈曲响应,分析了不同材料梯度变化参数下梁的过屈曲挠度随温度载荷变化的规律。
本文在已有的研究基础上,基于高阶剪切变形梁理论和Hamilton原理建立了功能梯度梁受热-机载荷共同作用下的几何非线性动力学控制方程。采用打靶法和Navier方法分别数值求解了在横向非均匀升温下功能梯度材料梁的热屈曲和自由振动响应,获得了高阶剪切变形梁在热坏境中的热屈曲规律及动态响应。
1 问题的数学模型
考虑一长为E、宽为E、高为E的功能梯度材料矩形截面梁。设轴向坐标为E,通过横截面的几何形心,横向坐标为E,其坐标原点在变形前的几何中面上。研究在横向非均匀升温下两端不可移简支(pinned-pinned)功能梯度材料梁的热屈曲和振动特性。
1.1等效物性参数
考虑梁的材料性质(弹性模量E、密度ρ、热膨胀系数α等)沿厚度方向按幂函数变化;则Reddy等给出了表征功能梯度复合材料(FGMs)的物性参数幂函数形式。设陶瓷材料体积含量沿厚度方向的变化为:
(1)
式中n(0≤n≤∞)为陶瓷材料的体积分数指数。则功能梯度材料梁的物性参数P(z)是材料成分百分比的函数[15]
P(Z)=Pm+Vc(z)(Pc-Pm)
(2)
n取不同值代表组分含量不一的功能梯度材料,n=0时退化为均匀各向同性陶瓷梁,n→∞时为金属梁。通常材料的泊松比v沿厚度方向变化很小,为了简化计算,这里假定v为常数。
1.2几何方程
基于von ka′rma′n几何非线性高阶剪切变形梁理论,其梁位移场可表示为
ψ(z)θ(x,t)
(3-a)
w(x,z,t)=w0(x,t)
(3-b)
式中:u0、w0为中面的位移;θ为中面法线剪切角。ψ(z)用来描述剪应变沿截面高度的分布;为了便于比较,给出不同剪切理论对应的ψ(z)表达式[10];经典梁理论(CBT)不考虑横向剪切变形,其ψ(z)=0;一阶剪切变形梁理论(FST),取ψ(z);高阶剪切变形梁理论取ψ(z)=z[1-1/3(z/(h/2))2]。
相应于位移场(1)的大挠度高阶剪切梁,其内任一点的应变-位移关系为
εx=εx(0)+zkx+ψ(z)ηx
(4)
1.3物理关系
考虑材料为线性热弹性,在热环境下与上述应变对应的轴向应力σx=和切向应力τxz分别表示为
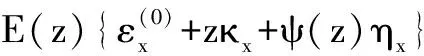
-E(z)α(z)ΔT(z,t)
(5)
(6)
其中,ΔT为温度的变化。沿梁的厚度方向,积分得到梁的薄膜力、弯矩、高阶弯矩和剪力表达式为
(7-a)
(7-b)
(7-c)
(7-d)
其中,C1、C2、C3、C4、C5、C6、B为刚度系数,定义为
(C1、C2、C3、C4、C5、C6)=
(8-a)
(8-b)
而NT、和ST分别为热薄膜力、热弯矩和高阶热弯矩。定义为
(9)
1.4运动方程及动力学控制方程
利用Hamilton原理
(10)
其中,T和U分别为功能梯度材料梁的动能和应变能,δW为外力虚功。
通过变分运算可得梁的运动方程为
(11-a)
(11-b)
(11-c)
其中,方程等号右端符号“.”表示对时间t求导。其中I1、I2、I3、I4、I5、I6为单位面积等效质量,分别定义为
(I1、I2、I3、I4、I5、I6)=
(12)
这里只考虑温度载荷对结构的响应,令qz=0。
将式(7-a)~式(7-d)、式(8-a)~式(8-b)、式(9-a)~式(9-b)代入式(11-a)~式(11-c)三式,考虑到式(4),可得位移形式的动力学控制方程
(13-a)
(13-b)
(13-c)
为方便分析计算,采用如下无量纲变换
(ξ,U,W)=(x,u0,w0)/l;
NT=l2T/C4;λ=(l/h)2αmTm
(14-a)
(D1,D2,D3,D4,D5,D6)=
(l2C1,lC2,lC3,lC4,lC5,lC6)/C4
(14-b)
(F1,F2,F4,F5,F6)=
(l2I1,lI2,lI4,I5,I6)C3/I3
(14-c)
(14-d)
可得问题的无量纲控制方程
(15-a)
(15-b)
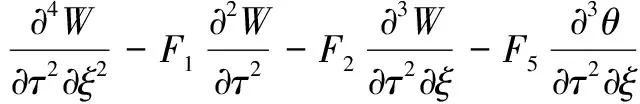
(15-c)
以及两端不可移简支(pinned-pinned)无量纲化的边界条件
U(0,τ)=0, W(0,τ)=0 M(0,τ)=0
U(1,τ)=0, W(1,τ)=0, M(1,τ)=0
(16)
式(15-a)~式(15-c)构成了功能梯度材料梁在湿热载荷同时作用下的几何非线性动力学无量纲控制方程,其中包含了轴向位移u0、W0,中面法线剪切角θ等3个基本未知函数,它们都是物质坐标和时间的函数。
2 控制方程的求解
在分析梁的热屈曲问题时,认为式(15-a)~式(15-c)与时间无关。即令方程等号右端为0,得
(17-a)
D4θ=0
(17-b)
(17-c)
由于方程式(17-a)~式(17-c)的强非线性和未知量之间的耦合效应,很难获得问题的解析解。因此,本文采用打靶法[15-16]寻求其数值解。首先,把两点边值问题转化为包含待定初始参数的初值问题。然后采用Runge-Kutta方法和Newton-Raphson法有机结合的数值方法不断调整这些未定的初始参数,使得初始问题的解也能满足终点处的边界条件,从而得到相应的边值问题的解。为了保证热过屈曲解和振动解在采用变步长四阶Runge-Kutta方法积分时具有相同的离散点,可将两个边值问题联立求解。
在分析梁的自由振动时,采用分离变量[17],设梁的位移函数为
(18-a)
(18-b)
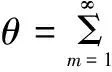
(18-c)
将式(18-a)~式(18-c)进行无量纲变换后代入到式(15-a)~式(15-c)中,可得到在热载荷作用下的自由振动的特征值问题无量纲方程。求解该方程,从而可获得固有频率以及相对应的位移模态。
3 数值算例与讨论
数值计算中,考虑梁为陶瓷氮化硅和金属SUS304两相材料制成的功能梯度材料,下表面为陶瓷,上表面为金属。其组分的材料物性参数见表1。
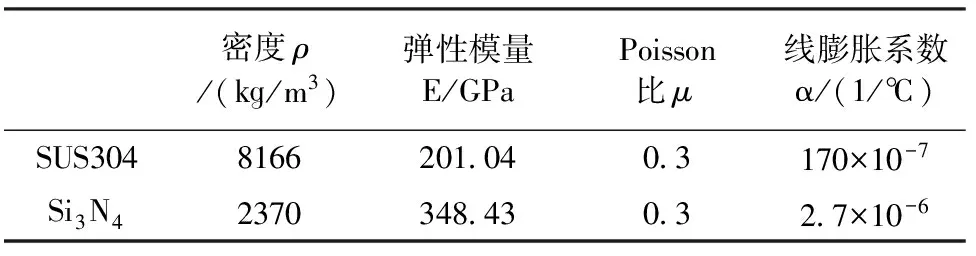
表1 功能梯度梁的物性参数
将功能梯度梁退化为均匀各向同性梁,并考虑只受均匀升温作用,得到无量纲临界升温的数值结果λcr=38.665,与精确解[18]λcr=4π2非常吻合。由此可说明本文理论分析和计算程序的正确性。
图1为在高阶剪切变形梁跨高比l/h=15,组分体积分数指数n=0下,取上下表面不同升温比值Tr=1.0,15,30时所得到的无量纲最大挠度与无量纲升温的关系曲线,此曲线为梁的热过屈曲载荷-变形曲线,从图1中可以看出,无量纲最大挠度W(1/2)随无量纲温度载荷的增大而相应增大,且为非线性关系。从图1中还可以看出,当λ为一定值时,随着上下表面升温比值的增大,无量纲最大挠度W(1/2)也增大,随着Tr的增大,无量纲临界温度λcr反而减小。图2给出了在高阶剪切变形梁跨高比l/h=15,无量纲升温λ=2、不同上下表面升温比值分别Tr=1,2,3为时无量纲热轴力NT与体积分数指数n的关系曲线。从图2中可以看出,给定其它参数,当体积分数指数n增大时,热轴力也相应增大。随着Tr的增大,热轴力NT也增大。

图1均匀材料梁最大挠度与无量纲温度的关系曲线(l/h=15,n=0)

图2无量纲热轴力与的关系曲线(l/h=15,λ=2)
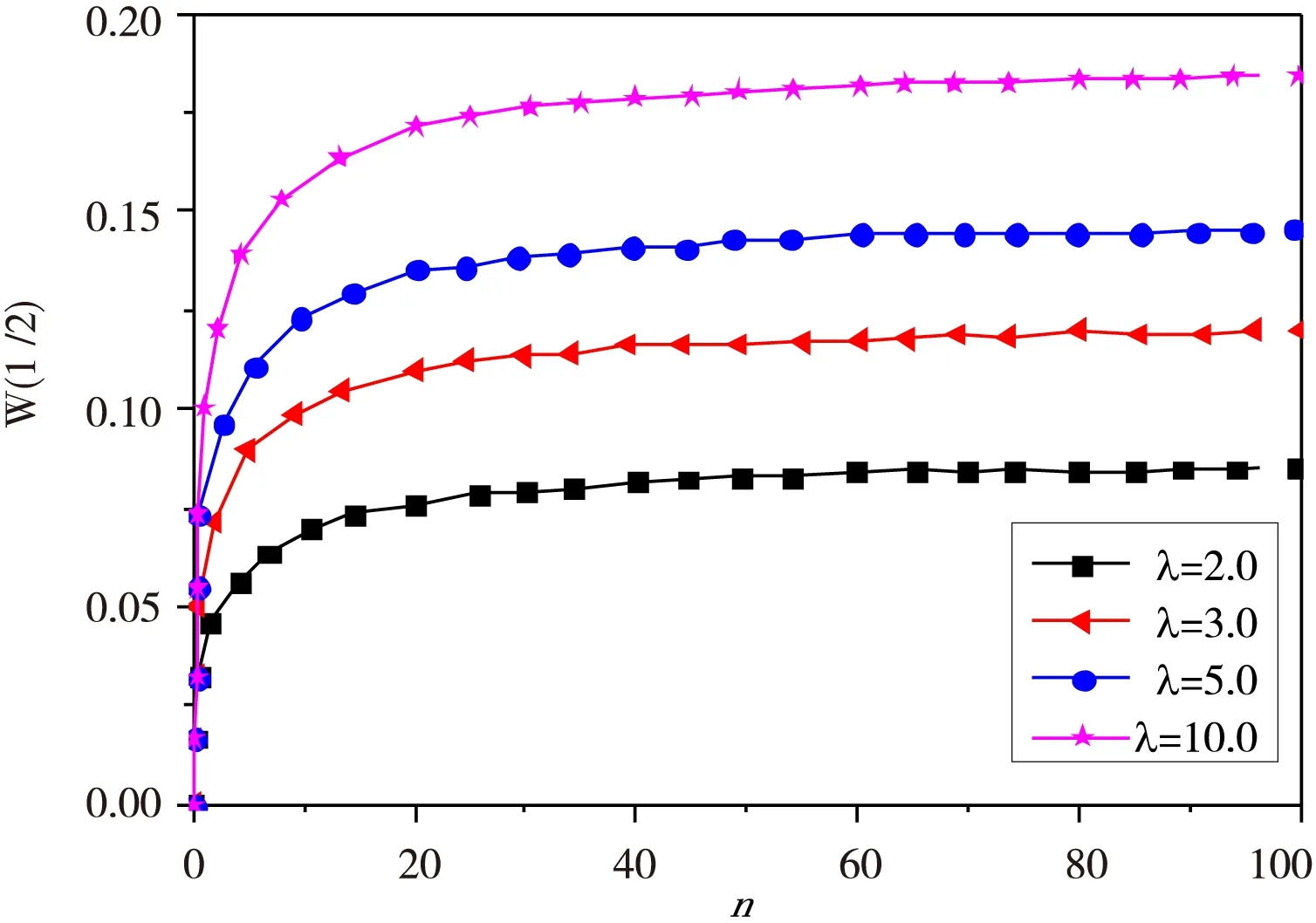
图3给定不同升温参数λ时W(1/2)与n的关系曲线
图3分别比较了当l/h=20,上下表面不同升温比值Tr=15时,不同温度下高阶剪切变形功能梯度材料梁的最大挠度随体积分数指数n的变化关系。从图3中可以看出,给定温度参数λ=2,3,5,10时,最大挠度随参数n的增加而增大,这是由于随着体积分数指数n的增加,功能梯度材料梁中金属SUS304的含量增加,陶瓷氮化硅含量减少,横截面的抗拉和抗弯刚度随n的增加而减少的缘故。因此FGM梁的抗弯刚度随n的升高而降低。图4 为给定不同弹性模量比值Ec/Em时高阶剪切梁无量纲升温λ随参数n的变化关系,从图4中可以看出,给定不同弹性模量比值Ec/Em=1.5,2.0,3.0时,无量纲升温λ随参数n的增大而逐渐减小,弹性模量比值Ec/Em越大,在同一体积分数指数n时,无量纲升温越小。
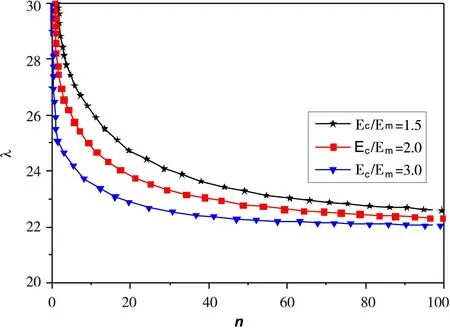
图4给定不同弹性模量比值时无量纲升温λ=0与材料梯度因子n的关系
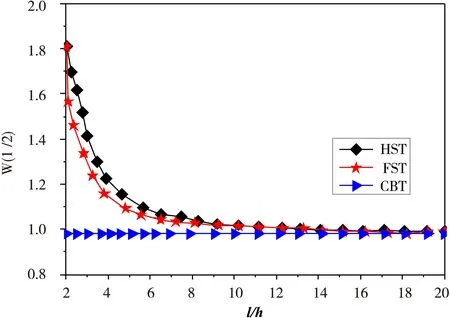
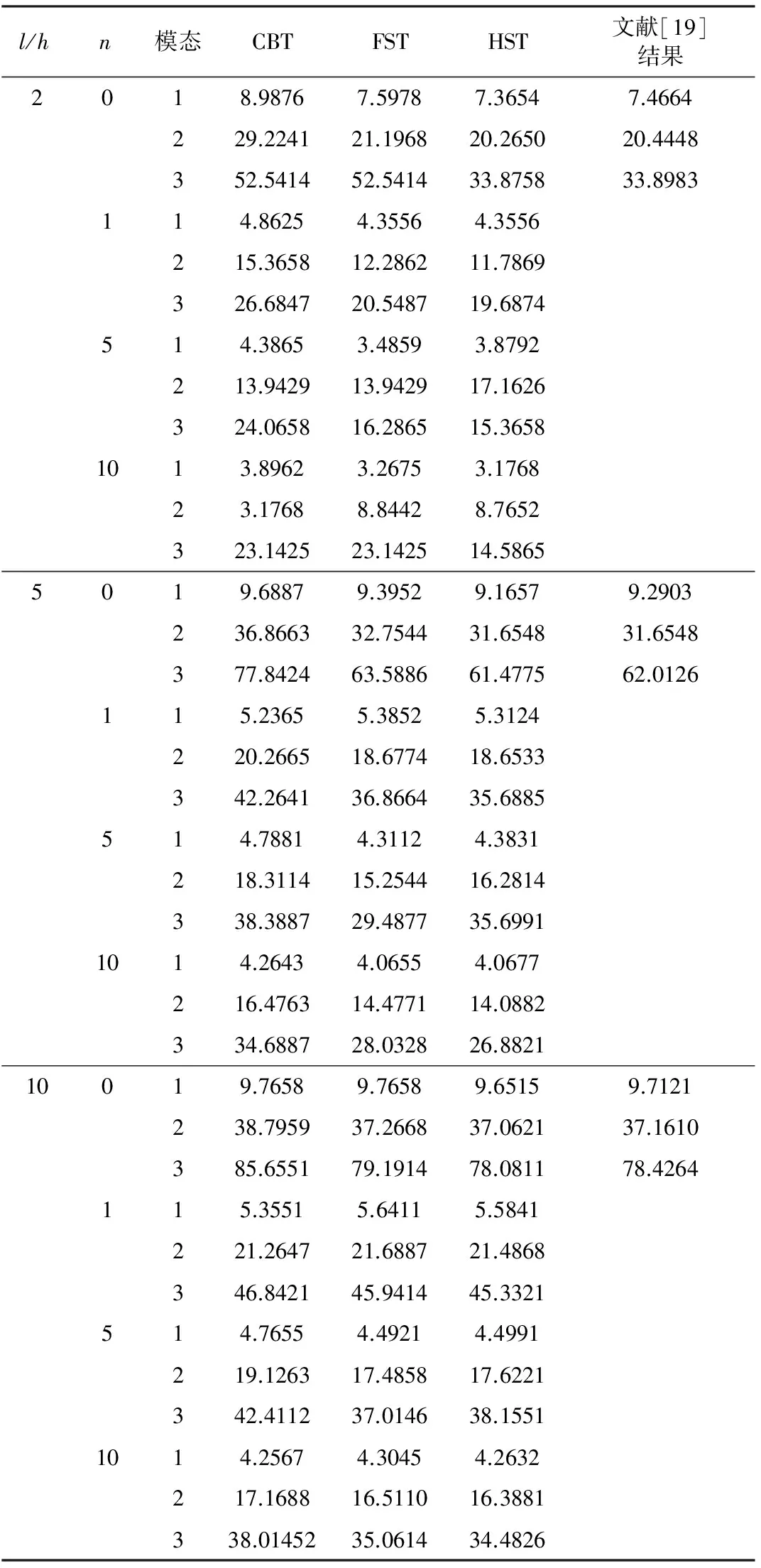
图5和图6分别给出了n=0、n=10的情形下,FGMs梁跨中挠度W(1/2)在不同的剪切理论作用下随跨高比的变化情况,从图中可以看出,各种剪切理论下梁的无量纲挠度随着梁高跨比l/h的增加越来越接近,在2≤l/h≤6之间,高阶剪切梁理论下功能梯度材料梁的无量纲挠度随跨高比l/h的变化较大,而6 图5n=0时不同剪切理论下无量纲挠度W(1/2)随跨高比l/h变化曲线 图6n=10不同剪切理论下无量纲挠度W(1/2) 随跨高比l/h变化曲线 表2给出了在梁跨高比分别为l/h=2、l/h=5和l/h=10,梯度因子分别为n=0、N=4、N=5及N=10的情形下,采用不同剪切理论所得到的FGM梁前3阶自然频率,并与已有的文献结果[19]进行比较来验证结果的正确性。可以看出,经典梁理论(CBT)预测的自然频率比一阶剪切理论(FST)和高阶剪切理论(HST)所预测的自然频率偏高。无量纲自然频率随梯度因子n的增大而减小。 表2 功能梯度梁前3阶自然频率的比较 基于von 几何非线性高阶剪切变形梁理论和Hamilton原理建立了功能梯度材料梁受热-机载荷共同作用时的几何非线性动力学控制方程。在研究静态热屈曲问题时,把方程退化成强非线性边值问题,采用打靶法数值求解该边值问题,获得了横向非均匀升温下梁的屈曲构型,绘出了梁的变形随温度载荷及材料梯度参数变化的特征关系曲线;研究动态响应时,采用Navier方法数值求解所建立的动力学控制方程,获得了横向非均匀升温下梁的自由振动响应,数值比较了不同剪切理论下梁的前3阶固有频率随跨高比、材料梯度参数变化的规律。结果表明,剪切变形、梁的跨高比、材料的非均匀性、温度变化对于高阶剪切功能梯度材料梁的变形及固有频率有很显著的影响。并且无量纲最大挠度随无量纲温度载荷的增大而相应增大,且为非线性关系。当无量纲升温参数为一定值时,随着上下表面升温比值的增大,无量纲最大挠度也增大,随着上下表面升温比值的增大,无量纲临界温度反而减小。 [1] 王保林,杜善义,韩杰才.功能梯度材料的热/机械耦合分析研究进展[J].力学进展,1999,29(4):528-548. [2] 仲政,吴林志,陈伟球.功能梯度材料与结构的若干力学问题研究进展[J].力学进展,2010,40(5):528-541. [3] 赵凤群,王忠民,刘宏昭.非保守力作用下FGM矩形板的稳定性分析[J].应用力学学报,2007,24(1):318-322. [4] DAI H L,RAO Y N.Nonlinear dynamic behavior of a long temperature-dependent FGM hollow cylinder subjected to thermal shocking[J].Science and Engineering of Composite Materials,2014,21(2):267-280. [5] 张靖华,潘双超,李世荣.热冲击下功能梯度圆板的动力屈曲[J].应用力学学报,2015,32(6):901-908. [6] SHEN H S.Nonlinear thermal bending of FGM cylindrical panels resting on elastic foundations under heat conduction[J].Composite Structures,2014,113:216-224. [7] SANKAR B V.An elasticity solution for functionally graded beams[J].Composites Science and Technology,2001,61(5):689-696. [8] CHAKRABORTY A,GOPALAKRISHNAN S,REDDY J N.A new beam finite element for the analysis of function ally graded materials[J].International Journal of Mechanical Sciences,2003,45(3):519-539. [9] BHANGALE R K,GANESAN N.Thermoelastic buckling and vibration behavior of a functionally graded sandwich beam with constrained viscoelastic core[J].Journal of Sound and Vibration,2006,295(1):294-316. [10] KHDEIR A A,REDDY J N.A remark on the state-space concept applied to bending,buckling and free vibration of composite laminates[J].Computers & Structures,1996,59(5):813-817. [11] KHDEIR A A,REDDY J N.Free vibration of cross-ply laminated beams with arbitrary boundary conditions[J].International Journal of Engineering Science,1994,32(12):1971-1980. [12] KHDEIR A A,REDDY J N.An exact solution for the bending of thin and thick cross-ply laminated beams[J].Composite Structures,1997,37(2):195-203. [13] 夏贤坤,沈惠申.功能梯度材料剪切板热屈曲后的非线性振动[J].振动工程学报,2008,21(2):120-125. [14] ZHU H,SANKAP B V.A combined fourier series galerkin method for the analysis of functionally graded beams[J].Journal of Applied Mechanics,2004,71(3):1-4.[15] 李世荣,张靖华,赵永刚.功能梯度材料Timoshenko梁的热过屈曲分析[J].应用数学和力学,2006,27(6):709-715. [16] LI S R,BATRA R C, MA L S.Vibration of thermally post-buckled orthotropic circular plate[J].Journal of Thermal Stresses,2007,30(1):43-57. [17] ZENKOUR A M.Generalized shear deformation theory for bending analysis of functionally graded plates[J].Applied Mathematical Modelling,2006,30(1):67-84. [18] 李世荣,程昌钧.加热弹性杆的热过屈曲分析[J].应用数学和力学,2000,21(2):119-125. [19] MATSUNAGA H.Vibration and buckling of deep beam-columns on two-parameter elastic foundations[J].Journal of Sound and Vibration,1999,228(2):359-376. The Static and Dynamic Response Analysis for Functionally Graded Materials Based on High Order Shear Under Heated CHANGXueping1,2,CHENGZhiqiang2,LIUBaosheng2 (1.School of Mechatronic Engineering, Southwest Petroleum University, Chengdu 610500, China;2.School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China) On the basis of the high order shear deformation beam theory, thermal buckling and free vibration of functionally graded beams with two-point boundary conditions were studied. Firstly, based on the high order shear deformation beam theory and the Hamilton principle, the geometric nonlinear dynamic control equations of the functionally graded beam were established. For the static thermal buckling problem, the equation was reduced into a nonlinear boundary value problem; numerical solution of the boundary value problem were obtained by using the shooting method; transversely non-uniform temperature rise buckling beam characteristic curves were plotted; and the law for deformation of the beam changing with the parameters of temperature gradient loading and material were obtained. Studying on dynamic response, dynamic control equations were solved by using Navier numerical method, and the free vibration response of the beam subjected to transverse non-uniform heating is obtained. Numerical comparison of the natural frequencies of the top 3 solutions with the span height ratio and the variation of the gradient parameters of the beam under different shear theory were made. The results showed that the shear deformation of beam, non-homogeneous materials, temperature change have a significant influence on the shear deformation and natural frequency of the beam. high order shear deformation theory; functionally graded material beam; thermal buckling; transverse non-uniform heating; free vibration 2016-03-30 国家自然科学基金项目(51105319);四川省教育厅重点项目(15ZB0053) 常学平(1978-),男,宁夏中卫人,讲师,博士,主要从事计算力学、复合材料结构力学等方面的研究,(E-mail)changxp@swpu.edu.cn 1673-1549(2016)03-0039-07 10.11863/j.suse.2016.03.09 TB115 A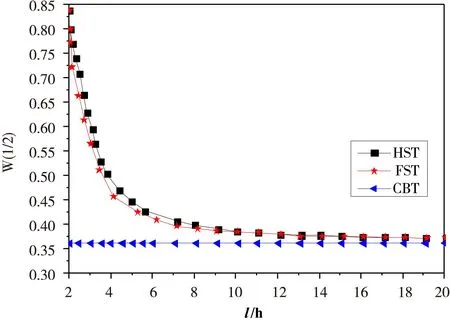
4 结束语
