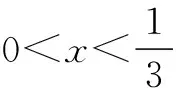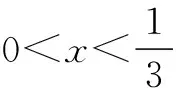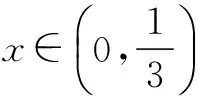含参不等式恒成立问题的求解策略
2016-11-04谢渊明
谢渊明
(甘肃省定西市岷县第一中学,748400)
含参不等式恒成立问题的求解策略
谢渊明
(甘肃省定西市岷县第一中学,748400)
含参不等式的恒成立问题是高考中的热点内容,它以各种形式出现在高中数学中的各部分内容中,扮演着重要角色.解决含参不等式恒成立问题的关键在于转化与化归思想的运用.从解题策略的角度看,一般而言,针对不等式的表现形式,有如下策略,供大家参考.
一、变换主元,转化为一次函数问题
处理变元较多不易消元的数学问题,可以选其中某个变元作为主元,而将其它变元看作常量,从而达到减元并简化解题过程的目的.
例1已知a∈[-1,1],不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为()
(A)(-∞,2)∪(3,+∞)
(B)(-∞,1)∪(2,+∞)
(C)(-∞,1)∪(3,+∞)
(D)(1,3)
解把原不等式左端看成关于a的一次函数,并记
f(a)=(x-2)a+x2-4x+4,
则f(a)>0对任意|a|≤1恒成立.易知只需
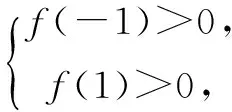
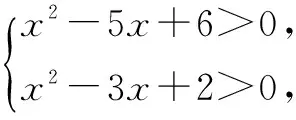
解得x<1或x>3,故选C.
例2已知对一切x∈R,不等式
恒成立,试确定a、b应满足的条件.
解因为x2-x+1>0恒成立,所以原不等式可化为(a-b)(x2-x+1)+(x+2)2>0,以a-b为主元.因为x2-x+1>0,(x+2)2≥0,且原不等式对于一切x∈R恒成立,所以a-b>0,即a>b为a、b应满足的条件.
评注在含参不等式成立的问题中,参数和未知数是相互制约、相互依赖的关系.若能转换两者在问题中的地位,则关于x的不等式就立即转化为关于参数的不等式,给人“山穷水复疑无路,柳暗花明又一村”之感.
二、联系不等式、函数、方程,转化为方程根的分布问题
例3已知x∈(0,+∞)时,不等式9x-m·3x+m+1>0恒成立,则m的取值范围是()
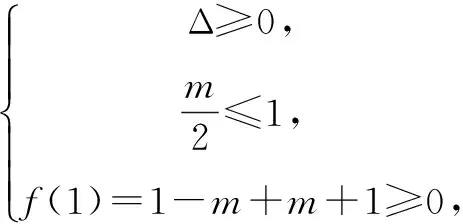
即m2-4m-4<0,
评注本题利用换元法简化了运算,但需要注意换元后自变量的取值范围.
三、构造函数求最值
解决这类问题常用两种方针:一是分离参数法.这种方法常用到下面结论:若函数f(x)存在最小值,则a≤(<)f(x)恒成立⟺a≤(<)f(x)min;若函数f(x)存在最大值,则a≥(>)f(x)恒成立⟺a≥(>)f(x)max.二是利用二次函数性质.
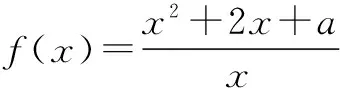
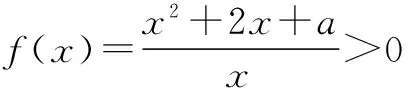
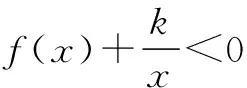
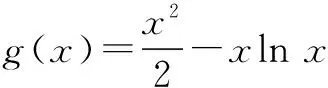
则g′(x)=x-(lnx+1)=x-1-lnx,
令h(x)=x-1-lnx,
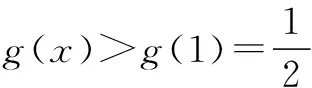
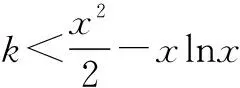
例6函数f(x)=x2+ax+3-a对任意x∈[-2,2]总有f(x)≥0成立,求a的取值范围.
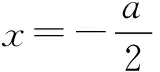
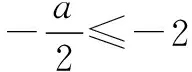
f(x)min=f(-2)=(-2)2-2a+3-a
=7-3a.
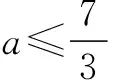
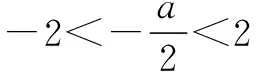
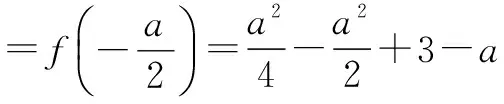
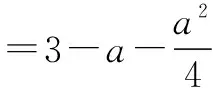
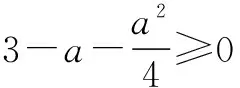
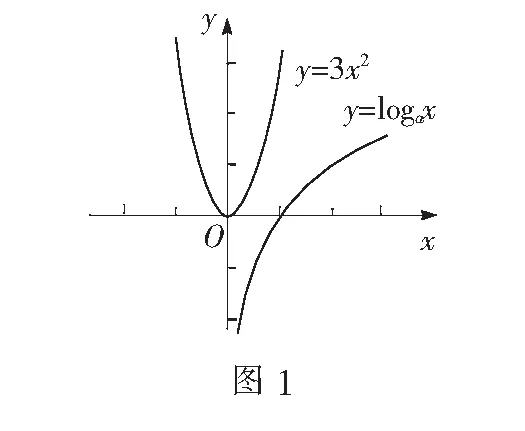
-6≤a≤2,∴-4 f(x)min=f(2)=7+a. 由7+a≥0,得a≥-7, ∴-7≤a≤-4. 综上,a的取值范围是[-7,2]. 例7在R上定义运算“*”:x*y=x(1-y).若不等式(x-y)*(x+y)<1对一切实数x恒成立,则实数y的取值范围是() (C)(-1,1)(D)(0,2) 解析由题意知,(x-y)*(x+y)=(x-y)[1-(x+y)]<1对x∈R恒成立. ∴12-4×(-1)×(y2-y-1)<0, ∴4y2-4y-3<0, 评注在不等式恒成立的处理中,若能画出不等式两边相应的函数图象,恒成立的代数问题立即变得直观化,对立的数量关系随之获得.数形结合可使求解过程简单快捷.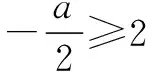
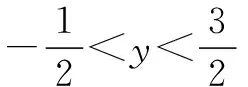
四、数形结合求参数