高中数学概念教学的思考与实践——以“互斥事件与对立事件”一课为例

符　鹰

(江苏省常州市田家炳高级中学,213000)



○教学研究○

高中数学概念教学的思考与实践
——以“互斥事件与对立事件”一课为例

符鹰

(江苏省常州市田家炳高级中学,213000)

概念课的教学在高中数学中有着相当重要的地位.教师只有好好钻研教材,合理创设情境,让学生将这些概念知识与以往知识体系相联系,做到融会贯通,由此改善学生的思维模式和学习习惯,培养他们的能力与素质,避免表面的反复的题目操作训练,才能让他们学好数学．在苏教版必修3的3.4中互斥事件第一节课“互斥事件与对立事件”就是一个好的概念课教学例子．互斥事件和对立事件是概率当中的两个基本概念,之前学生们已经学习了古典概型和几何概型.其实，对于基本的概率问题可以直接利用两种概率公式进行求解,而通过这节课的学习可以更简便地求较复杂的等可能事件的概率．当然,首先我们一定要让学生搞清楚这两个事件的概念是什么,可以与必修1学习的集合知识相联系进行讲解,从而让学生理解更透彻．在这节课的教学中，笔者认为不能把概念内容弱化,一味地希望通过做题让学生理解概念,而应该将概念讲解透彻,让学生做到举一反三,锻炼学生的数学思维能力,也让他们明白只有重视高中数学中基本概念知识,建立好知识体系,才能学好数学．笔者从基本概念和概率公式两个方面对这节课进行设计．

一、教学目标与重点、难点

了解互斥事件及对立事件的概念,能判断两个事件是否是互斥事件,进而判断它们是否是对立事件;

了解两个互斥事件概率的加法公式,知道对立事件概率之和为1的结论,会用相关公式进行简单概率计算;

注意学生思维习惯的培养,在顺向思维受阻时,转而采用逆向思维．

重点:对互斥事件和对立事件概念的理解和概率加法公式的掌握．

难点;互斥事件和对立事件之间的区别和联系．

二、教学设计思路

由于之前学习了古典概型的相关内容,可以先从一些简单的例子着手,一步步提出问题,逐步将学生引入到互斥事件和对立事件的概念中来,并且从集合的角度进行阐释；接着让学生通过例题巩固对两种事件的判断．然后,让学生通过例子观察一些事件的关系,从而举出和事件的概念,并得出互斥事件中和事件的概率公式以及对立事件的概率公式；接着再通过一些例子巩固对公式的理解．整个课堂教学当中,始终不忘初心——加强对两种事件概念的讲解.只有这样,才能避免学生在今后遇到相关问题时,因为判断错误而用错公式的情况发生．

三、课堂教学设计

1. 课题引入

引入2从1,2,3,4,5,6中任取一个数字,记事件A为“抽出的数字为2的倍数”，记事件B为“抽出的数字为3的倍数”，请阐述事件A和B的关系．

引入3老师拿出扑克牌．问:现在我手上一共有30张扑克牌,其中6张黑桃,7张红心,8张梅花,9张方块.现从中任意抽出一张,记事件A为“抽出的为黑桃”，事件B为“抽出的为红心”，事件C为“抽出的为梅花”，事件D为“抽出的为方块”，事件E为“抽出的牌为红色牌”，事件F为“抽出的牌为黑色牌”，请阐述事件A和B,事件C和D的关系．

设计意图引入1用学生非常熟悉的生活例子引起大家的对本节课的学习兴趣,最后的结果将在本节课结束之后揭晓．引入2与引入3实际上是为了通过学生的自主活动,让他们归纳出互斥事件的概念,从而得出什么是互斥事件．

2.在互斥事件概念基础之上提出彼此互斥事件以及对立事件的概念

问题1请观察引入3中还有哪些互斥事件?

问题2请观察引入3中事件E和事件F的关系?它们互斥吗?它们必定有一个发生么?

设计意图问题1目的是为了让学生观察并总结出来彼此互斥事件的概念,问题2的目的是为了引出对立事件的概念,继而在板书中得以体现．

问题3如果将A,B看成是事件A,B所包含的基本事件构成的集合,则符合什么条件时A,B互斥?什么时候A,B对立?

设计意图让学生通过与以前所学的集合知识相联系,同时在PPT中进行集合图形展示,从而加深对两种事件概念的理解,同时也提升了学生的知识迁移能力．

问题4从1,2,3,4,5,6,7,8,9这九个数当中任取两个数,给出下列事件：①恰有一个是偶数和恰有一个是奇数;②至少有一个是奇数和两个都是奇数;③至少有一个是奇数和两个都是偶数;④至少有一个是奇数和至少有一个是偶数.其中是互斥事件的是______,是对立事件的是______(填序号)．

设计意图笔者提示学生可以从集合的角度画出各个事件由基本事件构成的集合进行判断．学习了数学概念之后往往需要在丰富的情境中进行具体化,让学生们对概念的理解更深刻、更完善.学生们只有在具体实践之中自己总结出概念的真谛,才能将其注入到自己的数学知识体系当中．

3.得出A+B事件的概念,互斥事件当中和事件的概率公式,对立事件的概率公式

问题1引入3当中,从事件发生的角度看,事件E和事件B、D的关系如何?事件F和事件A、C的关系如何又如何?从概率角度看,它们的关系怎么样?

设计意图连续发问是为了引出和事件的概念,实际上事件E就是事件B+D,事件F就是事件A+C,让学生通过对事件A、B、C、D、E、F的概率计算得出．

问题2若在引入2中记“抽到的数字为2或3的倍数”为事件C,则事件C的概率为多少?

设计意图在讲解了和事件的概率公式之后再提出此问是为了让学生明白,只有互斥事件,才会有和事件的概率等于两事件概率之和．同时也强调了要在遇到具体问题时对概念进行多角度的辨析和理解的重要性．

设计意图根据和事件的概率公式得出对立事件的概率公式,从而又将公式复习了一遍．

4.解决问题，巩固概念

问题1某人射击1次,命中7～10环的概率如下表所示:

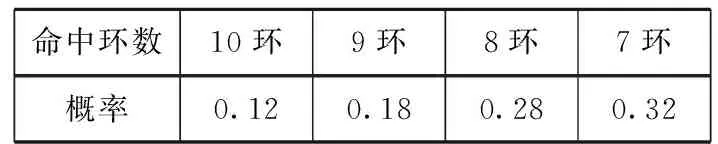
命中环数10环9环8环7环概率0.120.180.280.32

(1)求射击一次,至少命中七环的概率;

(2)求射击一次,命中不足七环的概率．

问题2一个袋里面装有大小形状相同的1个黑球,1个白球,1个红球,现在从中有放回地连续抽取三次．求(1)抽到的球颜色全相同的概率;(2)抽到的球颜色不全相同的概率．

问题3现在我们来看看一开始上课老师提出来的问题——我们班乒乓球比赛获得冠军的概率是多少?

设计意图问题1是苏教版教材第113页的例2,而问题2可以看作是问1的变式.从而向学生提出,在问题中遇到“至多”、“至少”“不全相同”等字眼时,可以考虑利用互斥事件和对立事件进行求解．问题3回答一开始引起大家学习兴趣的问题,启发大家数学实际上是生动有趣,融入生活的．

四、教学反思

在本节课当中,笔者始终紧扣概念教学,大部分时间花在引导学生通过自主活动得出互斥事件和对立事件的概念.引出概念之后,及时与必修1所学集合知识加以联系,让学生加深印象并培养了他们的知识迁移能力．然后通过例子让学生大胆猜想和事件的概率公式.数学当中很多定理公式都是先进行猜想再进行严格证明得到的,这也让学生们学习研究数学的一种基本方法．最后再利用例题让学生进一步熟悉相关概率公式．笔者整节课当中注重学生自主活动,利用PPT,投影等多媒体教学设备结合,让学生学起来更轻松,也更容易留下印象．

笔者一直认为高中数学中一些概念不应该直接生硬地教给学生,而应该通过一些具体情境让学生自己学会去体会、思考、总结.这种改善学生思维模式和学习习惯的方法也同样适用于一些定理公式的教学．高中数学概念课的教学过程一般分为操作——表象——定义——运用——体系,从学生在具体情境里自主操作到最终将概念知识融入到自己的数学知识体系中来．