谈中学数学习题变式的教学

何世方

(广西田东县田东中学，531599)



谈中学数学习题变式的教学

何世方

(广西田东县田东中学，531599)

一、问题的提出

习题是训练学生思维的材料,是教者引导学生掌握数学思想、方法以及分析问题和解决问题的技能技巧的载体．通过习题的变式教学可以帮助学生掌握数学的基本思想、基本方法以及学会用数学的思维方式去考虑问题、处理问题．

现在的教学资源很丰富,教学资料随处可得,用哪种资料的习题,不用哪种资料习题,教师和学生很难做出选择．根据笔者的教学经验,认为教师所选用的习题应“源于课本”,然后对它进行变式,使它“高于课本”.变式时要紧扣考试说明,以“考纲为纲”．

高考试题常常源于课本,根据课本习题进行变式.如何进行课本习题的变式教学，对此，本文谈谈自己的看法．

对于课本的习题,需要教师去领会和研究．在中学数学教学中,搞好习题变式的教学,特别是搞好课本习题的变式教学,不仅能加深基础知识的理解和掌握,更重要的是可以开发学生智力,培养和提高学生的数学素养．

二、习题变式教学的原则

习题变式教学,不同于习题课的教学,它与新授课、习题课和复习课并存,一般情况下不单独成课．因此,对于不同的授课,对习题的变式也应不同．例如,新授课的习题变式应服务于本节课的教学目的;习题课的习题变式应以本章节内容为主,适当渗透一些数学思想和数学方法;复习课的习题变式不但要渗透数学思想和数学方法,还要进行纵向和横向的联系,变式习题要紧扣考纲．在习题变式教学时,要根据教学目标和学生的学习现状,切忌随意性和盲目性．

选择课本习题进行变式,不要“变”得过于简单,过于简单的变式题是简单的“重复劳动”,影响学生思维的质量;难度“变”大的变式习题易挫伤学生的学习积极性,使学生难以获得成功的喜悦,长此以往,将使学生丧失自信心.因此,在选择课本习题进行变式时要变得有“度”．

在习题变式教学中,教师要让学生主动参与,不要总是教师“变”,学生“练”．要鼓励学生大胆地“变”,培养学生的创新意识和创新精神．

三、习题变式教学的方法

下面以一道习题为例,谈谈习题变式教学的方法．

原题1(高中数学(人教版)新教材必修1第39页习题1.3A组第1题)画出函数f(x)=x2-5x+6的图象,并根据图象说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数．

1.条件特殊化

条件特殊化是指将原题中一般条件,改为具有特定性的条件,使题目具有特殊性．将课本习题条件特殊化,引导学生挖掘条件,考察特定概念．例如,将原题改为:

变式1画出函数f(x)=|x2-5x-6|的图象,并根据图象说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数．

这不仅考察了绝对值的概念,也考察了解一元二次方程,这符合由一般到特殊的认识规律,学生容易接受．

2.改变背景

改变背景是指在某些条件不变的情况下,改变另一些条件的形式,使问题得到进一步深化．在教学过程中,变换习题的形式,可激发学生的探求欲望,从而提高学生的创新能力．例如,将原题改为:

变式2画出函数f(x)=x2-5|x|-6的图象,并根据图象说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数．

这样变式不仅考察了函数的图象,而且考察了偶函数的定义和性质.

变式3求函数f(x)=x2-5|x|-6在区间[-3,5]上的最值．

变式4求函数y=log2(x2-5x-6)的单调区间．

这样的变式练习,学生可以画图得出,也可以通过数学方法得出,通过这样的变式可以提高学生学习的兴趣,且能巩固基础知识,熟练常规解题,从而达到教学目的．

原题2在数列{an}中，a1=1，当n≥2时，若an-an-1=5，则数列{an}为等差数列，写出数列{an}的通项公式.

变式1在数列{an}中，当n≥2时，若a1=1,且an-an-1=n,求数列{an}的通项公式.

把等差数列中的常数d变为变量n,此时已不是等差数列，我们可以用迭加法来求数列{an}的通项公式.

∵n≥2时，

an=(an-an-1)+(an-1-an-2)+…

+(a2-a1)+a1

=n+(n-1)+(n-2)+d+a1

也可以把变式1的题目难度进一步加深：

(1)已知数列{an}满足a1=1,an-an-1=3n-1(n≥2)，求数列{an}的通项公式.

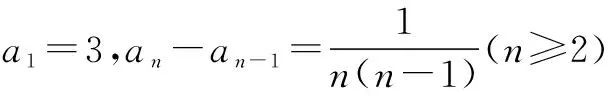
变式2在数列{an}中，当n≥2时，若a1=1，且an-can-1=d,求数列{an}的通项公式.

解析当c=1时，数列{an}为等差数列；

当c≠1，d=0时，数列{an}为等比数列；

当c≠1,d≠0时，我们可以用构造等比数列求数列{an}的通项公式.

方法如下：

设an+1+λ=c(an+λ),得

an+1=can+(c-1)λ.

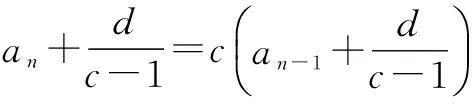
变式3在数列{an}中，若a1=1,且an+1-can=qn+1,求数列{an}的通项公式.

解析当c=1时，形式同变式1，也可用迭加法求通项公式；

当c≠1时， 我们也可以用构造等比数列求数列{an}的通项公式，方法如下：

对an+1=can+qn+1两边除以qn+1,化成

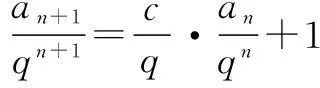
通过这样的变式一定能提高学生学习的兴趣，且能巩固基础知识，熟练常规解题，从而达到教学目的.

四、习题变式教学应注意的问题

1.源于课本,高于课本

在中学数学习题变式教学中,所选用的“源题”应以课本的习题为主.课本习题均是经过专家学者多次筛选后的题目的精品,我们没有理由放弃它．在教学中我们要精心设计和挖掘课本的习题,编制一题多变、一题多解、一题多用和多题一解以提高学生灵活运用知识的能力．

2.循序渐进,有的放矢

在中学数学习题变式教学中,对习题的变式要循序渐进,有的放矢．

例如,在高三复习时让学生做完习题：

一动圆与圆C1:(x+2)2+y2=1外切,与圆C2:(x-2)2+y2=9内切,求动圆圆心M的轨迹方程．

可将此题目变为:

变式1已知一个圆的圆心为坐标原点,半径为2,从这个圆上任一点P向y轴作垂线段PP1,垂足为P1,求线段PP1中点M的轨迹．

变式2已知圆C1:(x+2)2+y2=1与圆C2:(x-2)2+y2=9,若动圆M同时与两已知圆相外切,则动圆圆心M的轨迹是什么？

变式3已知圆C1:(x+2)2+y2=1与圆C2:(x-2)2+y2=9,若动圆M同时与两已知圆相内切,则动圆圆心M的轨迹是什么？

三个变式的目的都是让学生掌握利用圆锥曲线的定义求轨迹的方法．将常规题变为探索题．由常规题变出来的探索题,对学生来说更具创造性和挑战性．

3.“变式”要有度

习题变式教学，不同于习题课的教学，它惯穿于新授课、习题课和复习课，与新授课、习题课和复习课并存，一般情况下不单独成课.因此，对于不同的授课，对习题的变式也应不同.例如，新授课的习题变式应服务于本节课的教学目标；习题课的习题变式应以本章节内容为主，适当渗透一些数学思想和数学方法；复习课的习题变式不但要渗透数学思想和数学方法，还要进行纵向和横向的联系，同时变式习题要紧扣考纲.在习题变式教学时，要根据教学目标和学生的学习现状，切忌随意性和盲目性.

选择课本习题进行变式，不要“变”得过于简单，过于简单的变式题会让学生认为是简单的“重复劳动”，影响学生思维的质量.难度“变”大的变式习题易挫伤学生的学习积极性，使学生难以获得成功的喜悦，长此以往，将使学生丧失自信心.因此，在选择课本习题进行变式时要变得有“度”.

在习题变式教学中，教师要让学生主动参与，不要总是教师“变”，学生“练”.要鼓励学生大胆地“变”，培养学生的创新意识和创新精神.

总之，在中学数学习题变式教学中,习题的变式要紧扣《考试说明》,要以考纲为“纲”进行“变”;不要“变”出一些偏离考纲的“繁、难、杂”题目，以免浪费学生的宝贵学习时间和挫伤学生学习数学的兴趣．