浅谈数学课堂中的“探无止境”

杨敏良

(浙江省湖州市菱湖中学，313018)



浅谈数学课堂中的“探无止境”

杨敏良

(浙江省湖州市菱湖中学，313018)

数学探究是培养学生思维品质的重要的实践活动,所以探究教学应该是目前及今后较长一段时间都值得我们去运用的教学模式.可是，如何把握好问题的“探究点”，如何引导好学生的探究活动以及如何掌控好学生不同的探究方向产生的生成性内容等都是我们数学教育工作者需要不断研究的课题.

一、数学探究课堂的主要特征

1.自主性

数学探究改变了以往学生被动接受的学习方式,使学生积极主动地去探索、尝试以及谋求个体创造潜能充分发挥.这种教学模式将学生的需要、动机和兴趣置于核心地位,鼓励学生自主选择、主动探究.

2.合作性

现代教学理论认为,合作与交流是人本主义发展的重要部分,是主体之间的相互作用、相互交流、相互沟通、相互理解,是人基本的存在方式.合作与交流强调师生间、学生间动态的信息交流.在数学探究中,通过师生、生生间的交往,达到学生心态的开放、主体性的凸现、个性的张扬、创造思维的解放.

数学课堂是学生思维品质培养的主阵地,课堂教学的效率是促进学生有效学习的基本保障.课堂探究作为高效的教学模式已被绝对认可,而且在今后较长一段时间里将广泛运用.但笔者发现目前很多的课堂探究有流于形式之嫌,很多时候对问题的探究都只是“一探而过”,探而不究的课堂还时有发生,不但影响了课堂教学的效率,有时甚至会弄巧成拙.鉴于此，笔者想从自己的一堂探究课谈起，与大家讨论“探无止境”.

二、课堂探究环节再现

在高中数学必修2第一章解三角形的一堂复习课上笔者设计了如下问题让学生进行探究:

问题1在∆ABC中,三个内角A,B,C的对边分别是a,b,c,且A=60°,a2=b(b+c),求B.

(如此解决是在笔者的预料之中)

教师:很好,那么有没有其他的解法呢?

(经过进一步探究,有学生回答)

学生2:用cosB也可以做出来.

教师:不错,解法很漂亮,有没有同学有不同意见呢?

学生3:老师我也是用cosB做的.

即2sinAcosB=sinB+sinC,

教师:解法也很漂亮,以上两位同学给我们开了一个好头.我们得乘热打铁,请同学们再好好探究探究,看看有没有新发现,我很期待!

学生4:我觉得可以试试用cosC.

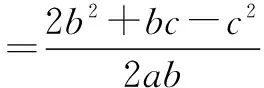
可化到这里就化不下去了.

教师:想法很好,正所谓“不怕做不到,就怕想不到”.同学们，我们齐心协力的时刻到了,我们要告诉这位同学:只要你敢想,我们就敢做,就算做不到我们也无怨无悔.

(一阵讨论之后,有学生站了起来)

学生5:刚才分式中的分子可以因式分解.

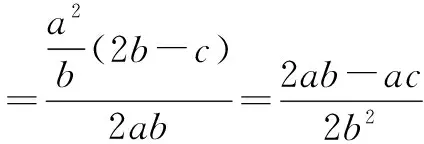
接下去就不知道了.

教师:艰难的一步啊,谢谢!下一步谁来?

学生6:右边可以跟方法3一样试试“边化角”：

即2sin2BcosC=2sinAsinB-sinAsinC.

接下去好像又不行了.

教师:我也来试试,我们来看等式的左边是3次,右边是2次,那么我们可以试试“统一次数”.显然左边降次操作性不强,我们可以将右边升次：

有2sin2BcosC=2sin(B+C)sinB-sin(B+C)sinC,

有2sin2BcosC=2sin2BcosC+2cosB·sinCsinB-sinBcosCsinC-cosBsin2C,

化简得2cosBsinB=sinBcosC+cosBsinC,即

sin 2B=sin(B+C)=sinA,

有A=2B或A+2B=180°(舍去),

所以B=30°.

教师:我成功了,不对,应该是我们成功了,因为我是“站在了巨人的肩膀上”才完成的(全班大笑).

教师:同学们,问题如此解决是“完美”了吗?接下来我们来回顾一下刚才的几个探究方向.显然，我们都是在走“余弦定理”的路线,而且我们坚持了“一条道走到黑”的信念,尝到了“功夫不负有心人”的喜悦.但有一个细节大家是否发现了,探究的最后我们都是把“边”转化成了“角”,也就是说“边化角”是此题的归宿,带着这个“归宿”让我们再看一眼已知条件“a2=b(b+c)”,不知道在座的各位“巨人”会不会有新发现?(沉默片刻后)

学生7:a2=b(b+c)这是“边的齐次式”可以直接“边化角”.

教师:很好,敢不敢试一试?

学生7:由a2=b(b+c),有

sin2A=sinB(sinB+sinC)，

即有sin2A-sin2B=sinBsinC,

然后……

教师:好的,再想一想.

学生8:可以降次，有

即cos 2B-cos 2A=2sinBsinC.

可得cos[(A+B)-(A-B)]-cos(A+B)+(A-B)]=2sinBsinC,

即2sin(A+B)sin(A-B)=2sinBsinC,

于是有sin(A-B)=sinB,

从而得到A-B=B或者A-B+B=180°(舍去),即A=2B,所以B=30°.

教师:看来我们探究题目真的可以说是“探无止境”.但同学们有没有发现其实学生1的方法是最简单的,而且我相信也是大家都容易想到的,那为啥我还一个劲地让大家再探究再探究呢?“问世间此山是否最高”，请看看下一题.

问题2在∆ABC中,三个内角A,B,C的对边分别是a,b,c,且A=80°,a2=b(b+c),求B.

教师:请问“学生1”的方法还能成功吗?

学生们:不行了.

教师:那其他的方法还能成功吗?

学生们:好像都行.

教师:所以我们解决一个题目的目的不是仅仅把它做出来就完事了,我们要养成“探其究竟”的习惯,树立“探无止境”的观念,要“探究一题攻克一类”,这样才能真正提高我们的思维能力,也就能提高我们的解题能力.(学生点头)

……

教师:既然说“探无止境”,那么大家有没有兴趣再探究一下“学生1”的方法,是真的不行了吗?(沉默片刻后,学生1再次回答)

2sinBcosA=sinC-sinB,

有2sinBcosA=sin(A+B)-sinB

=sinAcosB+cosAsinB-sinB,

有sinB=sinAcosB-cosAsinB

=sin(A-B).

从而得到A-B=B或者A-B+B=180°(舍去),即A=2B，所以B=30°

教师:很好,这才是真正的“探无止境”.

三、教学反思

在课堂教学中,师生的交流都是通过问题的逐个探究解决而得以实现的,学生在探究问题的过程中并非都能一探到底,磕磕碰碰甚至被卡壳是课堂上的常事.这时往往需要教师对学生进行鼓励,帮助其对困难进行分析,对学生可以突破的障碍进行适时点拨,让学生突破思维障碍,经过努力，体会成功后的喜悦.当然，对学生通过点拨后还是有困难的问题,教师可以挺身而出,作出详细的示范,让学生在不成功中获得宝贵的探究经验及解题教训.通过不断的“探其究竟”,使每一次探究都能实现“探究一题攻克一类”的目的.如此一定会逐步提高学生分析问题、解决问题的能力,也一定会逐步提高学生克服困难的勇气与信心,从而培养学生的思维品质.这样的课堂一定能成为学生有效学习的保障.

课前的教学设计是建立在教师的经验基础之上,带有很强的主观性.尽管也会考虑学生的实际状态,但学生是一个动态的、活动的主体,他们在探究过程中会出现怎样的情况,教师往往是无法估计的,从而导致在实际的课堂教学中我们常常会遇到一些突发事件.比如，对问题探究的方向的掌控有时会很难控制住,因为一旦放手让学生去探,你会体会到“三个臭皮匠顶个诸葛亮”的言之有理,更何况有些学生已经不是“臭皮匠”了.就像本堂课的问题探究中有些步骤的推理是笔者课前备课所没有设想好的,是学生探到了那个方向而带来了新的方法.所以笔者感叹道:我是站在了巨人的肩膀上.总之,由学生的需求而产生的探究,无论在知识的获取、情感的体验，还是思维品质的培养方面都胜过了老师的课前设计.我想只有通过这样的课堂,才能真正体会到数学探究的“探无止境”,也鞭策着我们数学教育工作者必须不断地加强解题研究,不断地提高自己探究问题、解决问题的能力,以及不断提高自己对课堂的驾驭能力.