球腔中氢键流体的吸附-解吸附转变:表面调控研究

李江涛, 刘书静,2, 顾　芳, 王海军,3

(1. 河北大学化学与环境科学学院, 保定 071002;2. 河北农业大学理学院, 保定 071001;3. 河北大学河北省化学生物学重点实验室, 保定 071002)



球腔中氢键流体的吸附-解吸附转变:表面调控研究

李江涛1, 刘书静1,2, 顾芳1, 王海军1,3

(1. 河北大学化学与环境科学学院, 保定 071002;2. 河北农业大学理学院, 保定 071001;3. 河北大学河北省化学生物学重点实验室, 保定 071002)

集中讨论了球形微腔表面对腔中氢键流体相态结构的调控机制. 为了揭示微腔表面对腔中氢键流体相平衡的影响, 首先根据吸附-解吸附原理并利用经典流体的密度泛函理论计算了微腔中氢键流体的平衡密度分布, 进而通过吸附-解吸附等温线及巨势等温线绘制出体系的相图. 在此基础上, 重点考察了球腔尺寸、 表面作用强度和作用力程对氢键流体毛细凝聚及层化转变的影响. 结果表明, 这些因素可以有效地调控体系毛细凝聚和层化转变的临界约化温度、 临界密度和相区大小等特征, 从而阐明了表面调控的主要机制. 研究结果为设计相关吸附材料提供了理论参考.

氢键流体; 吸附-解吸附; 毛细凝聚; 层化转变; 相平衡

随着纳米材料的迅速发展, 分子流体在纳米孔隙中的吸附-解吸附转变受到了广泛关注[1,2]. 研究表明, 吸附质在微腔中的相行为显著有别于其体相的相态特征. 在适当条件下, 纳米孔隙中不同类型的分子流体通常可以发生吸附-解吸附转变以及浸润-退浸润转变等诸多现象[3～23], 从而使毛细凝聚和层化转变成为相应的研究热点之一. 因此, 研究分子流体在不同纳米孔隙中的相平衡特征不仅可以揭示受限流体的相态结构, 也可为设计具有特定几何结构及吸附特性的功能材料提供参考. 实际上, 吸附质在纳米孔隙中的吸附行为除了受热力学因素影响以外, 主要取决于吸附质分子的自身性质及其与孔隙表面之间的相互作用[1～20]. 在以往的一些研究[8,9]中,流体与腔壁间的相互作用多以弱色散力表示, 因而相关研究工作主要探讨流体自身特征对其相态的影响. 然而, 随着表面修饰技术的不断提高, 基于表面调控方面的研究引起了研究者关注[23～26]. 本文利用经典流体的密度泛函理论[27,28]对球形微腔中氢键流体的相平衡进行探讨, 重点考察了微腔表面对氢键流体相态结构的影响. 为了揭示微腔表面对氢键流体相态结构的调控机制, 选择方阱势作为流体和腔壁间的相互作用, 进而详细研究了表面作用强度、 作用力程及球腔尺寸对氢键流体相态的调控机制.

1　微腔中氢键流体的密度泛函理论研究

自从基本度量理论(FMT)及改进的基本度量理论(MFMT)被提出以来[29～31], 经典流体的密度泛函理论研究已经取得了重要进展. 该理论指出, 对处于给定外势Vext(r)中且化学势为μ的流体而言, 其统计特征取决于体系以局域分子数密度分布n(r)为泛函变量的巨势泛函Ω[n(r)]

(1)

式中:F[n(r)]代表流体的内禀Helmholtz自由能, 由理想部分和过量部分构成, 即F[n(r)]=Fid·[n(r)]+Fex[n(r)]. 理想部分Fid[n(r)]=β-1∫{ln[n(r)Λ3]-1}n(r)dr,β-1≡kBT是Boltzmann常数kB与温度T的乘积; Λ为deBroglie热波长. 对于氢键流体, 过量自由能Fex[n(r)]由硬球、 色散和氢键3个部分构成, 其形式如下:

(2)

式中:Fhs[n(r)]表示分子间硬球相互作用的贡献, 在FMT和MFMT的框架下[29～31]可被写作:

(3)

式中的物理量Φ[nα(r)]以及加权密度nα(r)与球体的几何测度[29～31]直接相关. 式(2)中色散自由能Fdis[n(r)]也可通过微扰法[9]和权重密度近似[32,33]获得, 但鉴于本文主要考察的是表面对氢键流体吸附-解吸附的影响, 因而采用平均场近似来计算色散自由能, 具体形式如下:

(4)

式中:Vdis(|r-r′|)表示分别位于r和r′处的2个分子之间的相互作用势, 通常选作Lennard-Jones势, 即

(5)

式中:ε为色散能量,σ为流体分子的直径. 在具体计算中, 通常采用WCA近似进行处理[34]. 对于缔合流体而言, 其自由能可通过统计力学缔合流体理论[35], 并结合权重密度方法计算得到[36,37]. 对于本文考察的AaDd氢键流体, 相应的自由能可表示为[38,39]

(6)

式中:ρ(r)为坐标r附近的局域氢键数密度, 且ρ(r)与n(r)之间满足如下形式的质量作用定律[38]:

(7)

式中:εhb为氢键键能; ν为氢键的成键体积参数; ghs[n(r)]为硬球流体的径向分布函数[37].

(8)

式中:nb为氢键流体的体相分子数密度; μb为氢键流体相对于理想流体的过量化学势. 由式(2)可得μb=μhs+μdis+μhb, 其中,μhs,μdis和μhb分别代表体相流体的硬球作用、 色散作用和氢键作用的化学势[39].

为了研究球腔表面对氢键流体相态的调控机制, 假设在半径为R的球形微腔中, 当分子质心与球心的距离为r时, 分子与腔壁间的作用可用方阱势Vext(r)予以描述

(9)

式中:rm=R-σ/2,εsw(εsw<0)表示球腔表面与流体的吸引势能(通常称为作用强度或阱深), 而λσ则描述相应的吸引力程(亦称阱宽). 显然, 腔壁表面对流体相态结构的调控主要通过球腔半径R、 表面作用强度εsw和作用力程λσ得以体现.

众所周知, 流体的平衡密度分布是研究流体相关特征的基础. 由于流体与微腔表面之间的作用势Vext(r)具有球对称性, 因此流体的平衡密度分布亦然, 即n(r)=n(r). 式(8)表明, 为了得到流体的平衡密度分布, 需要输入初始密度然后进行迭代计算. 在计算中, 选取σ为单位长度并将球腔半径间隔0.01σ进行离散化, 相应的平衡判据为空间各点处前后2次的密度差均小于10-6, 且氢键的成键体积参数ν依照Segura等[40]的研究结果选择1.886×10-3σ3.

2　吸附-解吸附等温线及其平衡密度分布

鉴于此前已有氢键流体自身特征对其相态结构影响方面的讨论[39], 因此本文重点研究球腔半径(R)、 表面作用强度(εsw)和作用力程(λσ)的影响, 以期阐明球腔表面对氢键流体相态的调控机制. 为此, 选择A2D2型氢键流体系统进行考察并将氢键能量保持恒定(εhb/ε=25), 同时将约化温度T*定义为T*=kBT/ε.

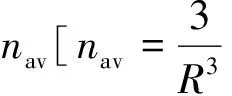
为了更加清晰地说明上述过程, 图1给出了A2D2型氢键流体的吸附-解吸附等温线及巨势等温线. 图1上半部分中左下方的迴滞线与氢键流体的层化转变相对应, 右上方的迴滞线则对应于氢键流体的毛细凝聚. 而图1下半部分则示出了相应的巨势等温线. 通过巨势的交点O(Q)作垂线, 进而得到其与图1上半部分中吸附-解吸附等温线的交点O′和O″(Q′和Q″), 此即该约化温度下微腔内流体的相平衡点. 进一步改变约化温度, 可得出吸附-解吸附等温线随着约化温度的变化趋势, 如图2所示, 其上、 下两部分的迴滞线分别表示毛细凝聚和层化转变随着约化温度的变化趋势. 显然, 当约化温度较低时, 氢键流体的层化转变和毛细凝聚同时存在, 而随着约化温度的升高, 层化转变渐渐消失并最终与毛细凝聚融合在一起.

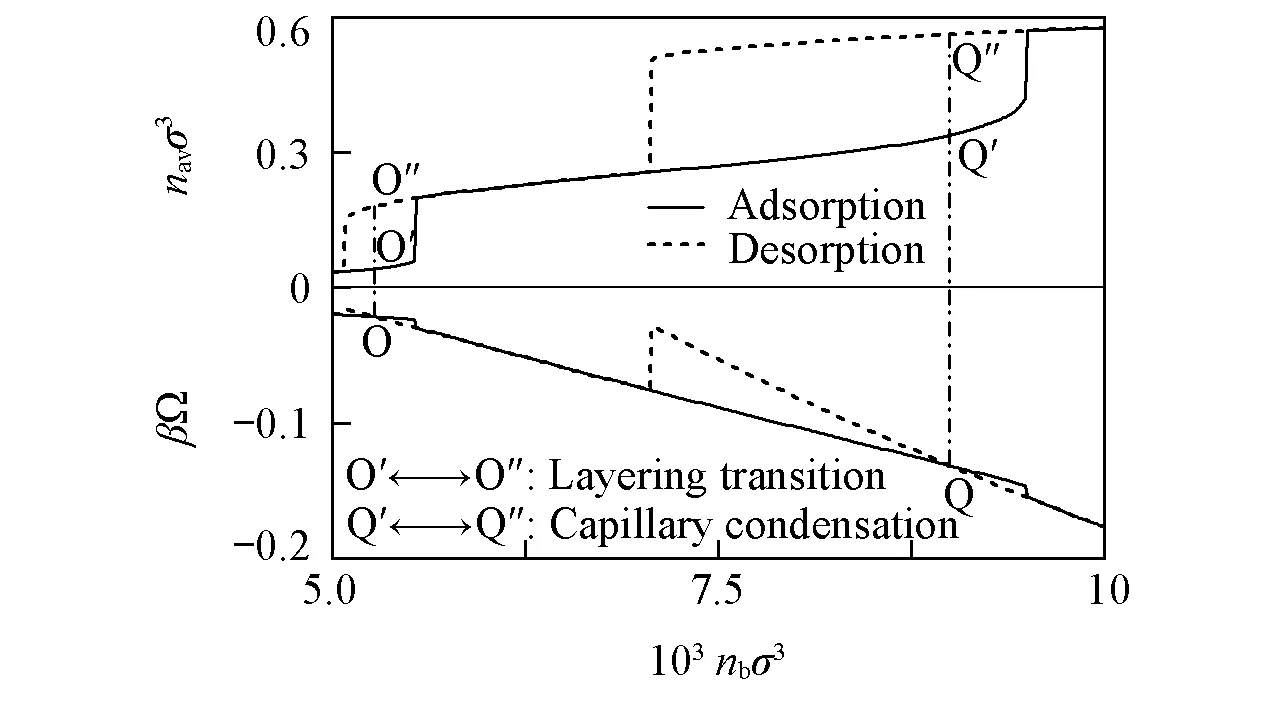
Fig.1　Adsorption-desorption isotherms and the corresponding grand potential isotherms for Hydrogen bonding(HB) fluid of A2D2 type Condition:R=7.5σ; λ=0.75; T*=3.3; εsw/ε=25.

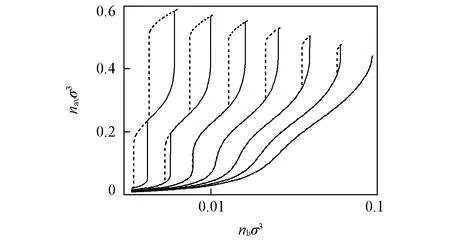
Fig.2　Adsorption-desorption isotherms for HB fluid of A2D2 type for different T*Condition:R=7.5σ; λ=0.75; εsw/ε=25, where T* from left to right is 3.2 to 3.8 with interval of 0.1.

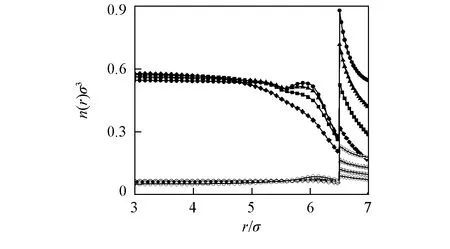
Fig.3　Density profiles of gas-like(hollow line) and liquid-like(solid line) HB fluid of A2D2 type for different strengthen parameters R=7.5σ; λ=0.5; T*=3.6, εsw/ε:◇ ◆ 10; □ ■ 15; △ ▲ 20; ○ ● 25.

Fig.4　Density profiles of gas-like(hallow line) and liquid-like(solid line) HB fluid of A2D2 type for different range parameters λ R=7.5σ; λ=15; T*=3.6, λ:○ ● 0.25; □ ■ 0.50; △ ▲ 0.75.

实际上, 在考察微腔中氢键流体的相行为时, 直接受表面作用影响的物理量是流体的平衡密度分布. 需要指出的是, 有关微腔中流体相平衡研究中的平衡密度分布与流体密度给定时的平衡分布有着本质差别:前者需要根据吸附-解吸附原理来确定, 通常存在类气和类液2种密度分布, 而后者仅为给定密度下的平衡分布, 并无气液之分. 图3和图4分别给出了表面作用强度和作用力程变化时氢键流体的平衡密度分布. 图3和图4结果表明, 表面作用强度和作用力程均可显著影响腔中氢键流体的平衡密度分布. 特别是当作用力程较大时(λ=0.75), 表面附近的类气和类液两相密度也较为接近. 当得到相应的平衡密度分布之后, 即可进一步计算不同条件下氢键流体的统计特征, 并对相关因素予以分析.

3　球腔表面对氢键流体相态的调控

如上所述, 腔壁表面对流体聚集态结构的调控因素主要包括球腔半径(R)、 作用强度参数(εsw/ε)和作用力程参数(λ). 根据吸附-解吸附等温线和相应的巨势等温线, 可以给出这些因素变化时体系的相图, 进而得到相关因素对体系相态的影响.

3.1球腔尺寸对氢键流体相态的影响

图5给出了在εsw/ε=25和λ=0.75的条件下, 球腔半径变化时氢键流体的相图, 显然其与体相相图有明显差异. 首先, 当球腔半径小于某个临界值时, 腔中氢键流体存在2类明显不同的相区, 其中左侧分支代表氢键流体的层化转变, 而右侧分支则代表毛细凝聚, 且二者以体相气-液共存线作为边界. 这意味着相对于体相氢键流体而言, 微腔中氢键流体的相态结构更加丰富. 当球腔半径大于某个临界值时, 层化转变和毛细凝聚逐渐融合, 且随着球腔半径的增加, 相应的临界相区也逐渐接近体相的气-液共存线. 其次, 腔中氢键流体毛细凝聚的临界约化温度均高于层化转变的临界温度, 且当球腔半径增加时, 左、 右两支的临界约化温度均随球腔半径的增大而升高, 并且层化转变相的临界约化温度的升高更为显著. 事实上, 这一变化趋势与受限流体的普遍规律相一致[2,41]. 同时, 层化转变的临界密度随着球腔半径的增大而增大, 而毛细凝聚的临界密度则随之减小. 此外, 当球腔半径增加时, 毛细凝聚的相区随之增大, 而层化转变的相区则逐渐减小并最终与毛细凝聚的相区融合.

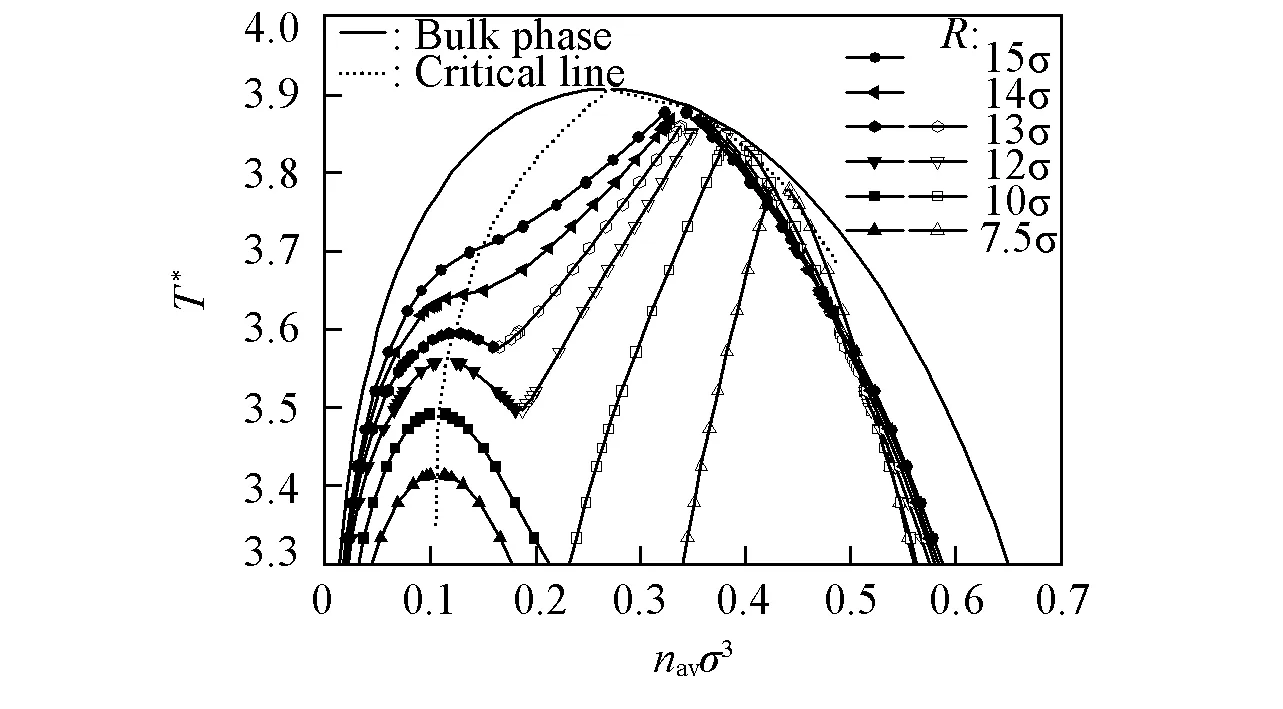
Fig.5　Phase diagram of confined HB fluid of A2D2 type for different R values Condition:εsw/ε=25; λ=0.75.

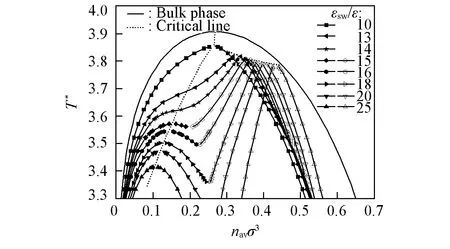
Fig.6　Phase diagram of confined HB fluid of A2D2 type for different εsw/ε values Condition:R=7.5σ; λ=0.75.

3.2表面作用强度对氢键流体相态的调控

图6给出了在R=7.5σ和λ=0.75的条件下, 表面作用强度变化时流体的相图. 可见, 球腔表面的作用强度对氢键流体相行为的调控主要体现在以下3个方面:(1) 当作用强度高于某个临界值时, 腔中氢键流体的层化转变和毛细凝聚同时存在, 而当其低于该临界值时, 层化转变和毛细凝聚则相互融合; (2) 当毛细凝聚和层化转变同时存在时, 毛细凝聚的临界约化温度均高于层化转变的临界约化温度; 同时, 随着作用强度的增加, 层化转变和毛细凝聚的临界约化温度均逐渐降低, 但前者的降幅大; (3) 在临界密度方面, 当作用强度增加时, 毛细凝聚的临界密度随之增大, 而层化转变的临界密度则随其增大而减小. 此外, 层化转变的临界约化温度和临界密度之间基本呈线性关系.

3.3表面作用力程对氢键流体相态的调控

Fig.7　Phase diagram of confined HB fluid of A2D2 type for different λ values Condition:R=7.5σ, εsw/ε=25.

图7所示为在R=0.75σ及εsw/ε=25的条件下, 表面作用力程变化时体系的相图. 可见, 球腔表面作用力程对氢键流体相行为的调控主要表现为:(1) 当作用力程小于某个临界值时, 氢键流体的层化转变和毛细凝聚发生融合, 而当作用力程大于该临界值时, 层化转变和毛细凝聚则同时存在; (2) 当层化转变和毛细凝聚同时存在时, 毛细凝聚的临界约化温度均高于层化转变的临界约化温度; 同时, 层化转变和毛细凝聚的临界约化温度均随着作用力程的增加而降低, 但是前者降低幅度较为明显; (3) 当作用力程增加时, 层化转变的临界密度随之减小, 而毛细凝聚的临界密度则随之增大. 此外, 层化转变的临界约化温度和临界密度之间基本呈线性关系.

综上, 球腔表面对氢键流体的相行为具有显著的调控作用. 从球腔尺寸、 表面作用强度和作用力程对受限氢键流体相图的影响可知, 毛细凝聚和层化转变的临界约化温度、 临界密度和相区等均与表面作用直接相关. 由此可知, 通过对表面的改性(改变微腔尺寸、 作用强度和力程)可以实现对腔中氢键流体相态结构的有效调控. 根据这些结果, 可以有针对性地对微腔表面进行修饰, 从而调控腔中氢键流体的相态结构, 为设计相关的吸附材料提供参考.

[1]József T.,Adsorption:Theory,ModelingandAnalysis, Marcel Dekker, New York, 2002, 105—173

[2]Dunne L. J., Manos G.,AdsorptionandPhaseBehaviorinNanochannelsandNanotubes, Springer, New York, 2010, 241—255

[3]Evans R.,JPhys.:Condens.Matter, 1990, 2(46), 8989—9007

[4]Malo B. M., Pizio O., Patrykiejew A., Sokolowski S.,J.Phys.:Condens.Matter, 2001, 13(7), 1361—1379

[5]Hadjiagapiou I. A.,Phys.Rev.E, 2002, 65(2), 021605

[6]Neimark A. V., Ravikovitch P. I., Vishnyakov A.,Phys.Rev.E, 2002, 65(3), 031505

[7]Gatica S. M., Cole M. W.,Phys.Rev.E, 2005, 72(4), 041602

[8]Li Z. D., Cao D. P., Wu J. Z.,J.Chem.Phys., 2005, 122(22), 224701

[9]Fu D., Li X. S.,J.Chem.Phys., 2006, 125(8), 084716

[10]Peng B., Yu Y. X.,J.Phys.Chem.B, 2008, 112(48), 15407—15416

[11]Wu H. S., Li X. S.,ActaChim.Sinica, 2010, 68(17), 1681—1686(吴慧森, 李小森. 化学学报, 2010, 68(17), 1681—1686)

[12]Ravikovitch P. I., Neimark A. V.,Langmuir, 2006, 22(26), 10864—10868

[13]Wu J. Z.,J.Phys.Chem.B, 2009, 113(19), 6813—6818

[14]Baksh M. S. A., Yang R. T.,AIChE.J., 1991, 37(6), 923—926

[15]Ravikovitch P. I., Neimark A. V.,Langmuir, 2002, 18(5), 1550—1560

[16]Henderson D., Sokolowski S.,Phys.Rev.E, 1995, 52(1), 758—762

[17]Takaiwa D., Hatano I., Koga K., Tanaka H.,PNAS, 2008, 105(1), 39—43

[18]Neimark A. V., Lin Y. Z., Ravikovitch P. I., Thommes M.,Carbon, 2009, 47(7), 1617—1628

[19]Milischuk A. A., Ladanyi B. M.,J.Chem.Phys., 2011, 135(17), 174709

[20]Brovchenko I., Oleinikova A.,J.Phys.Chem.B, 2011, 115(33), 9990—10000

[21]Liu Y., Zhao S. L., Wu J. Z.,J.Chem.TheoryComput., 2013, 9(4), 1896—1908

[22]Li L. B., Vorobyov I., Allen T. W.,J.Phys.Chem.B, 2013, 117(40), 11906—11920

[23]Wang W., Yuan Y., Sun F. X., Zhao M., Ren H., Zhu G. S.,Chem.Res.ChineseUniversities, 2014, 30(6), 1018—1021

[24]Wen M. X., Zhang Y. M.,Chem.J.ChineseUniversities, 2014, 35(5), 1011—1015(文孟喜, 郑咏梅. 高等学校化学学报, 2014, 35(5), 1011—1015)

[25]Du Y., Chen H. J., Cheng Z. J., Lai H., Zhang N. Q., Sun K. N.,Chem.J.ChineseUniversities, 2014, 35(1), 105—109(都颖, 陈海杰, 成中军, 来华, 张乃庆, 孙克宁. 高等学校化学学报, 2014, 35(1), 105—109)

[26]Li S. S., Liao M. Y., Jin M. H.,Chem.Res.ChineseUniversities, 2014, 30(3), 518—520

[27]Evans R.,Adv.Phys., 1979, 28(2), 143—200

[28]Ramakrishnan T. V., Yussouff M.,Phys.Rev.B, 1979, 19(5), 2775—2794

[29]Rosenfeld Y.,Phys.Rev.Lett., 1989, 63(9), 980—983

[30]Yu Y. X., Wu J. Z.,J.Chem.Phys., 2002, 117(22), 10156—10164

[31]Roth R., Evans R., Lang A., Kahl G.,J.Phys.:Condens.Matter, 2002, 14(46), 12063—12078

[32]Yu Y. X.,J.Chem.Phys., 2009, 131(2), 024704

[33]Peng B., Yu Y. X.,Langmuir, 2008, 24(21), 12431—12439

[34]Weeks J. D., Chandler D., Anderson H. C.,J.Chem.Phys., 1971, 54(12), 5237—5247

[35]Chapmann W. G., Gubbins K. E., Jackson G., Radosz M.,FluidPhaseEquilib., 1989, 52, 31—38

[36]Yu Y. X., Wu J. Z.,J.Chem.Phys., 2003, 119(4), 2288—2295

[37]Yu Y. X., Wu J. Z.,J.Chem.Phys., 2002, 116(16), 7094—7103

[38]Wang H. J., Hong X. Z., Gu F., Ba X. W.,Sci.ChinaB, 2006, 49(6), 499—506

[39]Gu F., Wang H. J., Fu D.,Sci.ChinaChem., 2013, 43(1), 55—62(顾芳, 王海军, 付东. 中国科学B辑, 2013, 43(1), 55—62)

[40]Segura C. J., Chapman W. G., Shukla K. P.,Mol.Phys., 1997, 90(5), 759—771

[41]Yu Y. X., Gao G. H., Wang X. L.,J.Phys.Chem.B, 2006, 110(29), 14418—14425

(Ed.:V, K)

† Supported by the National Natural Science Foundation of China(Nos.21374028, 21306034), the Natural Science Foundation of Hebei Province, China(No.B2014201103), the Youth Foundation from Educational Committee of Hebei Province, China(No.QN20131079) and the Project for Top Young Talent of Hebei Province, China.

Adsorption-desorption of Hydrogen Bonding Fluid Confined in a Spherical Cavity:the Role of Surface Regulation†

LI Jiangtao1, LIU Shujing2, GU Fang1*, WANG Haijun1,3*

(1. College of Chemistry and Environmental Science, Hebei University, Baoding 071002, China;2.CollegeofScience,AgriculturalUniversityofHebei,Baoding071001,China;3.ChemicalBiologyKeyLaboratoryofHebeiProvince,HeibeiUniversity,Baoding071002,China)

The effect of surface regulation on the phase behavior of hydrogen bonding(HB) fluid confined in a nano-spherical cavity was investigated by phase equilibrium thermodynamics. We tried to reveal the important role of cavity surface playing in the adsorption-desorption transition of confined HB fluid when the fluid-surface interaction is a square-well potential. In this study, density functional theory for classical fluids was used together with the modified fundamental measure theory. It was found that the cavity surface could give rise to significant effects on the critical temperatures, critical densities and phase regions of layering transition and capillary condensation. As a result, one can regulate the phase equilibria and aggregated state of the HB fluid by changing the strength and range of fluid-surface interaction and the radius of spherical cavity. It is expected that the present study is helpful to design related adsorption materials or to study the phase behavior of nano-fluids.

Hydrogen bonding fluid; Adsorption-desorption; Capillary condensation; Layering transition; Phase equilibria

10.7503/cjcu20160078

2016-01-30. 网络出版日期:2016-08-17.

国家自然科学基金(批准号:21374028, 21306034)、 河北省自然科学基金(批准号:B2014201103)、 河北省高等学校科学技术研究项目(批准号:QN20131079)及河北省青年拔尖人才项目资助.

O641

A

联系人简介:顾芳, 女, 博士, 副教授, 主要从事高分子凝聚态理论研究. E-mail:fanggu@hbu.edu.cn

王海军, 男, 博士, 教授, 博士生导师, 主要从事高分子凝聚态理论研究. E-mail:whj@hbu.edu.cn