小学数学中的运算和运算定律
2016-11-03胡重光
胡重光 周 志
小学数学中的运算和运算定律
胡重光 周 志

运算是小学数学的主要内容,关于运算的基本理论无疑是小学数学教师必须掌握的。但是,我国的小学教师一般都没有系统地学习它,小学教师培训一般也没有数学基础知识的内容。本文拟对运算和运算定律及其教学作一个扼要的介绍。
一、运算的概念
在数学中,运算是再普通不过的事了。但是要回答什么是运算却并不容易说清楚。我国的小学数学界至今没有给出运算的定义,却给加、减、乘、除都下了定义。比如,加法的一种定义是:把两个数合成一个数的运算叫做加法。说加法是一种运算,但之前并没有说什么叫运算,这样我们还是不知道什么是加法。再如,什么叫“把两个数合成一个数”也没说清楚。1和2合成12,也是把两个数合成了一个数。这样的定义我们曾长期使用,至今仍在流行。
考察加、减、乘、除这些运算,可以发现它们具有一些共同点:都是在两个数之间进行的,都按照某种法则进行,结果都得到一个确定的数。苏联数学家M. K.格列本卡和C.E.里亚平合著的《算术》(这本书是苏联师范专科学校的教科书。我国北师大教授郝新将其译成中文,由高等教育出版社出版)一书中给运算下的定义就是:
设给定两数a与b,根据已知的规则,由给定的两数来求新数叫做运算。
这一定义显然是按照上述三个特点作出的。但是运算的结果不一定得到新数,例如1×1=1。定义没有说求得的新数是一个还是不只一个。如果限于我国目前小学数学的范围,则可以说结果是一个确定的数。仿照这两位数学家给出的定义,我们可以给小学数学中的运算下一个定义:
定义1:给定两个数,依照某种法则,由这两个数求得一个确定的数叫做运算。
这个定义基本上体现了运算的本质,也比较通俗易懂。
运算的更一般的定义可从张禾瑞的《近世代数基础》中找到。该书用集合和映射的观点给代数运算下了定义。算术运算是代数运算的特例。该书所定义的运算,其结果是唯一的。
二、自然数的运算
有了运算的定义,我们就可以据此定义加、减、乘、除了。这几种运算的区别,在于它们的运算法则不同。由于法则不同,所得的结果一般也不同。这四种运算的结果分别有不同的名称:和、差、积、商。首先我们在自然数的范围内考察运算。
(一)自然数的加法
定义2:设a、b是两个自然数,从a起数b+1个数,数到的最后一个数叫做a与b的和。
例如,2与3的和,就是从2起数4个数:2、3、4、5,数到的最后一个数是5,所以2与3的和是5。
这一定义既规定了什么是两个自然数的和,也给出了求两个自然数的和的方法。
根据这两个定义,我们就可以给加法定义如下:
定义3:求两个自然数的和的运算,叫做自然数的加法。
(二)自然数的减法
对于减法,我们可以用同样的方法定义。首先定义两个自然数的差:
定义4:设a、b是两个自然数,b≤a。从a起倒数b+1个数,数到的最后一个数叫做a与b的差。
例如,3与2的差,就是从3起倒数3个数:3、2、1,数到的最后一个数是1,所以3与2的差是1。
然后给出减法的定义:
定义:5:求两个自然数的差的运算叫做自然数的减法。
由差的定义可以看出,减法是加法的逆运算。加法与减法的关系可以用下面的算式表示:
如果a+b=c,那么c-b=a或c-a=b。
因此,我们也可以这样定义减法:
定义5’:已知两个加数的和以及其中一个加数,求另一个加数的运算叫做减法。
根据这个定义,我们可以利用加法来做减法。例如,由2+3=5即可得出5-2=3或5-3=2。
(三)自然数的乘法
我们通常将乘法定义为同数连加的简便运算。这一定义也是长期使用并流行至今的。但它并没有说明什么是乘法,因为简便运算这一概念是不明确的。为了定义乘法,同样要先定义乘积。
定义6:(1)设n是正整数,m是自然数,n个m相加的结果叫做m与n的乘积,简称积,记作m×n。
(2)m与0的积为0:m×0=0。
(3)m与1的积为m:m×1=m。
例如,3个2相加的结果,叫做2与3的积,记作2×3。特别地,0×3=0+0+0=0。
但是,3×0不能认为是0个3相加,3×1也不能认为是1个3相加(在这里当然不能利用乘法的交换律把3×0转化为0×3)。然而从现实问题不难得到3×0、m×1、0×0的正确结果。例如:
数学课上老师出了3道思考题,每做对1道思考题老师奖3颗五角星。丁丁做对了2道思考题,亮亮做对了1道思考题,晶晶没做对1道思考题,三人各得了几颗五角星?
这道题的数量关系是:
每道题奖励的五角星数×做对题数=得到的五角星数
丁丁得的五角星数是:3×2=6(颗),
亮亮得的五角星数是:3×1=3(颗),
晶晶得的五角星数是:3×0=0(颗)。
晶晶没有做对思考题,当然得不到五角星,由此可知0乘3的积应当是0。
如果再添一问:晶晶得了几面红旗?因为老师只奖五角星,不奖红旗,就是说,做对1道思考题奖励的红旗面数是0,晶晶做对了0道,所以她得的红旗面数是:0×0=0(面)。
这样我们又得出0乘0的积为0。
这样的例子是小学生也可以理解和信服的。
有了定义中的(2)、(3)两条,则乘法交换律对任意自然数都成立了。
乘积的定义隐含一个顺序:m×n表示n个m相加,即m表示相同加数,n表示相同加数的个数。在传统教材中,这一点是十分明确的。但自2000年开始课改以来,新教材认为不必区分乘数和被乘数,一律称为因数。3个2相加既可写作2×3,也可写作3×2。从乘法的意义虽然可以得出2×3与3×2结果相同,但两者的意义并不同。买3斤橘子每斤2元与买2斤橘子每斤3元显然不能混为一谈。因此,我们可以不区分乘数和被乘数,但不能不区分2×3与3×2,不能因为学生易错就放弃原则。
类似地,乘法的定义是:
定义7:求两个自然数的乘积的运算叫做自然数的乘法。
(四)自然数的除法
除法的意义有两种。一种是等分除法,即把一个数平均分成若干份,求每份是多少。例如,将12平均分成3份,求每份是多少。方法是看哪个数乘3等于12。因为3×1=3,3×2=6,3×3=9,3×4=12,所以12÷3=4。另一种是包含除法,即求一个数包含几个另一个数。例如,求12包含几个4。方法是看4的几倍等于12。因为4×1=4,4×2=8,4×3=12,所以12÷4=3。由此我们看到,除法可定义如下:
定义8:已知两个因数的积与其中一个因数,求另一个因数的运算叫做除法。
除法有一个重要的性质,就是0不能做除数。通常我们这样说明其道理:
设a÷0=b,那么0×b=a。若a≠0,那么这样的b不存在,即这个除法没有商;若a=0,那么b可以为任意数,即这个除法的商可以是任意一个数。
这个道理看起来很有说服力,但对小学生讲却是不合适的,因为儿童总是从实际意义方面看问题的。我们可以把一个数(或量)平均分成几份,如果一人独占也可以说只分成1份,但是平均分成0份显然是说不通的。我们可以说6里面包含几个3、几个2、几个1,但是说6里面包含几个0显然也是说不通的。这样的解释儿童是可以理解的。
自然数中的四则运算还有一个重要的不同之处:加法和乘法对任意两个自然数都能实施,但减法只有在被减数不小于减数时才能实施,除法受的限制最大,只有在能整除时才能实施。对于一个正整数n,可以实施n+1次减法运算,除法则远少于这个数字。现实生活中有余数的除法是常见的,能整除的除法则是不常见的。因此,教学中应该多出现有余数的除法。
自集合论流行以来,基数理论被广泛使用。例如,美国的卡尔B·艾伦多弗写了一本专供小学教师使用的书《关于算术和几何的原理》就是只用基数理论的。该书的加法定义是:
n(A)+n(B)=n(A∪B),
即a+b=n(A∪B)。
书中举例说:要说明2+3=5,我们采取以下步骤:
(1)选取集合A,使n(A)=2,即选取的集合有2个元素。
(2)选取集合B,使n(B)=3,a并使A与B不相交。即选取的B有3个元素,其中没有一个是A的成员。
(3)构成A∪B。
(4)找出n(A∪B)=5。
(5)然后用等式a+b=n(A∪B)定义加法。
显然,这一定义相当繁琐,并且它没有给出加法的法则。进一步我们还会发现,按这一定义证明加法结果的唯一性、加法的运算定律等都比较复杂。更重要的是,学前儿童是自发地用数数的方法计算加法的。
序数理论受到一些著名数学家的高度重视,M.K.格列本卡和C.E.里亚平在《算术》一书中强调指出:“数数的观念以及与它联系着的自然数列的观念在算术中是极其重要的。”弗赖登塔尔对序数和基数理论作了很多论述。他高度评价序数理论:“无论从历史的、发生的还是从系统的角度来看,数的序列都是数学的基石。可以说,没有数的序列就没有数学。”“儿童很早就开始学计数了,并把它当成一种乐趣。他们的计数能力要远远超出对数量的理解。……数的概念产生中,计数数是最初始的,最具有意义的。”“我更深入的想法是利用完全归纳法,以计数数来奠定自然数及其运算的基础。这是一种典型的,简捷可靠、富有创造力的方法。”“加法是继续计数,减法是往回计数,这是传统的教学法中的一项基本原理。形成这项正确原理的灵感来自于数的计数这个侧面,然而它却被新数学的教学法专家忽视了。”“自然数的数量侧面并不足以成为自然数引入的基础,它的效果不大,漏洞却不小。”
用序数理论定义加法,由于自然数的性质决定了数数的结果是唯一的,立刻就可得出加法结果的唯一性。
这样,计数也归结于数数。根据皮亚诺公理,每一个自然数都存在唯一的后继数,所以得:
由和的定义以及定理1立即得到:
由乘法的定义可知,乘法是特殊的加法,因此乘积是唯一存在的。
由于差是用倒数的方法得到的,所以当减法能够实施时,其差是唯一的。
若两个数的除法可以实施,那么商是唯一的,这一点可以证明如下:
假设a除以b(b≠0)得到两个商q和q′,q≠q′,那么a=bq且a=bq′。由此得bq=bq′,b(q-q′)=0。
因为b≠0,所以q-q′=0,于是q=q′。这与假设矛盾,商的唯一性得证。
关于计数,还有一个重要的计数公理:
根据这一公理,可以很容易地得出加法的交换律
a+b=b+a
因为a+b意味着先数a个数,接着数b个数;b+a意味着先数b个数,接着数a个数。即交换加数的位置相当于改变数数的顺序。
加法的结合律(a+b)+c=a+(b+c)的实质也是数数顺序的改变。
由于乘法是特殊的加法,乘法的运算定律也可以用计数公理说明,下面将结合运算定律的教学进行介绍。
三、运算定律的教学
教材对加法和乘法的交换律与结合律都采用了用具体例子说明的方法教学。例如,加法交换律的教学如图1所示(其他运算定律的教学结构完全相同)。

图1
显然,这里用的是不完全归纳法,因此教材的推理是有逻辑漏洞的。但教材没有把这一漏洞告诉学生,这样学生就会产生数学并不需要十分严谨的印象。事实上,用不完全归纳法是很容易犯错误的。举一个最简单的例子,素数都是奇数,无论考察多少个大于2的素数都正确。但事实上大家都知道这是一个假命题。小学数学虽然要求浅显易懂,但应该是浅而不错,易而有理。这里应该如斯托利亚尔在《数学教育学》一书中指出的:“在教学过程中,必须尽可能公开指明逻辑上的不得已的漏洞,而不能对学生隐瞒。”
其实,加法交换律可以利用图来说明(如图2)。
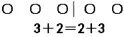
图2
从左往右数是3+2,从右往左数是2+3,根据计数公理,应有3+2=2+3。
还可以利用数轴来说明(如图3)。
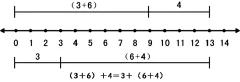
图3
乘法的交换律和结合律也可用类似的图形模式或实物操作来说明(如图4、图5所示)。
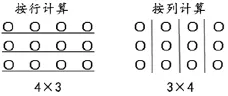
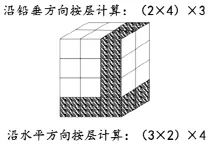
图5
由图4可以得出:4×3=3×4;
由图5可以得出:(2×4)×3=3×(2×4)=(3× 2)×4。
这些图虽然只涉及具体例子,但它提供了一个形象的模式,学生从中可以看出,图中小圆圈的个数和长方体的层数都是可以任意给定的。由此他们体会到,上述运算定律具有一般性。需要注意的是,图5是立体图,中年级的儿童观察它可能有一定的困难,最好采用实物操作的方法,用小立方块拼出这个长方体。还可设计一个活动让学生自己操作、计算,则更有意义。
如果作出下面的两个图(如图6、图7)还可分别得出:a+b=b+a,m×n=n×m(字母都代表正整数)。
这可以说具有一般性了。
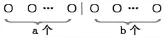
图6
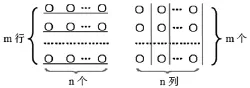
图7
我国的小学数学课程没有介绍乘法和除法的分配律,但这两个定律分别是多位数乘法和除法法则的依据。它们也可以用类似的图(如图8、图9)来说明。
12×3=(10×3)+(2×3):

图8
39÷3=30÷3+9÷3:

图9
(本文是基金项目:湖南省教育科学规划课题(XJK013CJC004)、湖南省省级重点建设学科“课程与教学论”建设项目资助的阶段性成果)
(作者单位:湖南第一师范学院长沙市实验小学)
